Экономико-математическое моделирование производства
1. Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одно животное, чтобы затраты были минимальными? Использовать данные таблицы:
| Питательное вещество | Количество питательных веществ в 1 кг корма | |
| 1 | 2 | |
А В | 2 2 | 1 4 |
| Цена 1 кг корма, тыс. руб. | 0,2 | 0,3 |
Построить экономико-математическую модель задачи, дать необходимые комментарии к ее элементам и получить решение графическим методом. Что произойдет, если решать задачу на максимум, и почему?
Решение:
Введем обозначения:
Х1 – количество корма 1 вида;
Х2 – количество корма 2 вида.
Целевая функция – F = 0,2 х1 + 0,3 х2
Ограничения: 2х1+1х2≥6
2х1+4х2≥12
х1, х2≥0
Решим задачу графическим способом
Первое ограничение имеет вид 2х1+1х2≥6, найдем пересечение с осями координат
| Х1 | 0 | 3 |
| Х2 | 6 | 0 |
Второе ограничение 2х1+4х2≥12, найдем пересечения с осями координат
| Х1 | 0 | 6 |
| Х2 | 3 | 0 |
Для определения направления движения к оптиму построим вектор – градиента Їс (с1;с2), координаты которого являются частными производными целевой функции, т. е. с (0,2;0,3).
Этот вектор показывает направление наискорейшее изменение функции.
Прямая f(х) = 0,2х1 + 0,3х2 = а1, перпендикулярная вектору – градиенту, является линией уровня целевой функции.
Для нахождения координат точки максимума решаем систему
2х1 + х2 = 6
![]() 2х1 + 4х2 =12
2х1 + 4х2 =12
-3х2 = -6
![]() х2 = 2
х2 = 2
2х1+2=6
2х1 =4
![]() х1 =2
х1 =2
Ответ: (2;2)
Fmin = 0,2*2+0,3*2=0,4+0,6=1
График:
Ответ: чтобы затраты были минимальными необходимо расходовать 2ед. первого корма и 2 ед. второго корма.
Если данную задачу решать на максимум, то задача не имеет решения, так как целевая функция не ограничена сверху, т. е Fmax=+∞
2. Для изготовления четырех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цены реализации единицы каждого вида продукции приведены в таблице.
| тип сырья | норма расхода сырья на одно изделие | запасы сырья | |||
| А | Б | В | Г | ||
| 1 | 1 | 0 | 2 | 1 | 180 |
| 2 | 0 | 1 | 3 | 2 | 210 |
| 3 | 4 | 2 | 0 | 4 | 800 |
| цена изделия | 9 | 6 | 4 | 7 | |
Требуется:
1. Сформулировать прямую оптимизационную задачу на максимум выручки от реализации готовой продукции, получить оптимальный план выпуска продукции.
2. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теории двойственности.
3. Пояснить нулевые значения переменных в оптимальном плане.
4. На основе свойств двойственных оценок и теорем двойственности:
- Проанализировать использования ресурсов в оптимальном плане исходной задачи;
- Определить, как изменяется выручка и план выпуска продукции при увеличении запасов сырья 2 и 3 видов на 120 и 160 единиц соответственно и уменьшении на 60 единиц запасов сырья 1 вида;
- Оценить целесообразность включения в план изделия Д ценой 12 единиц, на изготовление которой расходуется по две единицы каждого вида сырья.
Решение:
1. Сформулируем экономико – математическую модель задачи.
Переменные:
х1- количество единиц продукции А,
х2- количество единиц продукции Б,
х3- количество единиц продукции В,
х4- количество единиц продукции Г.
Целевая функция: F=9х1+6х2+4х3+7х4 →max,
Цель максимизировать выручку от реализации готовой продукции
Ограничение:
![]() По 1 типу ресурса: 1х1+0х2+2х3+1х4≤180,
По 1 типу ресурса: 1х1+0х2+2х3+1х4≤180,
По 2 типу ресурса: 0х1+1х2+3х3+2х4≤210,
По 3 типу ресурса: 4х1+2х2+0х3+4х4≤800,
По смыслу х1;х2;х3;х4 ≥0.
Решение задачи выполним с помощью надстройки Excel Поиск Решения. Выбираем результат поиска решения в форме отчета Устойчивости.
Полученное решение означает, что максимальную выручку 2115 ден. ед., можем получит при выпуски 95 ед. продукции А и 210 ед. продукции Б. При этом ресурсы 2 и 3 типа будут использоваться полностью, а из 180 ед. сырья 1 типа будет использоваться 95 ед. сырья.
Сформулируем экономико–математическую модель двойственной задачи
Переменные:
у1- двойственная оценка ресурса 1 типа, или цена 1 ресурса,
у2- двойственная оценка ресурса 2 типа, или цена 2 ресурса,
у3- двойственная оценка ресурса 3 типа, или цена 3 ресурса.
Целевая функция двойственной задачи: необходимо найти такие «цены» у на ресурсы, чтобы общая стоимость используемых ресурсов была минимальной. G=b1*y1+b2*y2+…→min
G=180у1+210у2+800у3→min
В исходной задачи четыре переменных, следовательно в двойственной задаче четыре ограничения.
![]() по виду продукции А: 1у1+0у2+4у3≥9,
по виду продукции А: 1у1+0у2+4у3≥9,
по виду продукции Б: 0у1+1у2+2у3≥6,
по виду продукции В: 2у1+3у2+0у3≥4,
по виду продукции Г: 1у1+2у2+4у3≥7
по смыслу у1; у2; у3≥0
2. Найдем оптимальный план двойственной задачи, используя теоремы двойственности:
По 2 теореме- yi*(∑aij*xj-bi)=0
у1*(1х1+0х2+2х3+1х4-180)=0
у2*(0х1+1х2+3х3+2х4-210)=0
у3(4х1+2х2+0х3+4х4-800)=0
Если х=(95;210;0;0), то
у1(95-180)=0, т.к. 95<180=>у1=0
у2(210-210)=0
у3(4*95+2*210-800)=0
хj(∑aij*уi-cj)=0, если хj>0, то ∑aijуi=cj
![]()
![]() х1=95>0=> у1+4у3=9 у3=9/4=2,25
х1=95>0=> у1+4у3=9 у3=9/4=2,25
х2=210=> у2+2у3=6 у2=6-2*9/4=1,5
у1=0 у1=0
Результат: Оптимальный план у=(0;1,5;2,25)
F(х)=2115
G(y)=180*0+210*1,5+800*2,25=315+1800=2115=>первая теорема о двойственности f(х)=g(у) выполняется.
3. Поясним нулевые значения переменных хi в оптимальном плане.
Если ∑ aijуi>сj, то хj=0
У нас х3=0,х4=0=>затраты на изделия В и Г превышают цену (См. отчет по устойчивости в столбце нормируемая стоимость).
4. а) Анализ использования ресурсов в оптимальном плане
Если уi>0, то ∑ aijxj= bi, i=1,….,m,
Если ∑ aijxj< b, то уi=0, i=1,….,m.
У2=1,5; у3=2,25=>сырье 2 и 3 полностью используются в оптимальном плане и являются дефицитными, т.е. сдерживают рост целевой функции.
Сырье 1 используется не полностью 95 из 180 это сырье не влияет на план выпуска продукции, т.е. не ограничивает рост целевой функции, общая стоимость используемых ресурсов g (0;1,5;2,25)=2115.
б) Если запасы сырья изменить 1-120, 2-330, 3-920, то выручка составит 2565 при оптимальном плане (65;330;0;0), остаток сырья 1 типа составит 120-65=55.
в) Если включить в план изделие Д ценой 12 единиц, на изготовление которого расходуется по 2 единицы каждого сырья, то выручка составит 2268 при оптимальном плане (112;142;0;0;34), при этом сырье будет полностью израсходовано.
3. Промышленная группа предприятий (холдинг) выпускает продукцию трех видов, при этом каждое из трех предприятий группы специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции одного вида: первое предприятие специализируется на выпуске продукции первого вида, второе предприятие – продукции второго вида, третье предприятие – продукции третьего вида. Часть выпускаемой продукции потребляется предприятиями холдинга (идет на внутреннее потребление) остальная часть поставляется за его пределы (внешним потребителями, является конечным продуктом). Специалистами управляющей компании получены экономические оценки aij(i=1,2,3; j=1,2,3) элементов технологической матрицы А (норм расхода, коэффициентов прямых материальных затрат) и элементов уi вектора конечной продукции У.
Требуется:
1.Проверить продуктивность технологической матрицы А=(аij) (матрицы коэффициентов прямых материальных затрат).
2.Построить баланс (заполнить таблицу) производства и распределения продукции предприятий холдинга.
| предприятия | коэффициенты прямых затрат | конечный продукт | ||
| 1 | 2 | 3 | ||
| 1 | 0,0 | 0,1 | 0,2 | 180 |
| 2 | 0,1 | 0,2 | 0,1 | 200 |
| 3 | 0,2 | 0,1 | 0,2 | 200 |
Таблица матричного баланса
| конечный | валовый | ||||
| предприятие | потребляющие | продукт | продукт | ||
| производящие | 1 | 2 | 3 | ||
| 1 | 0 | 33,1 | 72,6 | 180 | 285,7 |
| 2 | 28,5 | 66,2 | 36,3 | 200 | 331 |
| 3 | 57,1 | 33,1 | 72,6 | 200 | 362,8 |
| усл чист продукция | 200 | 198,7 | 181,3 | 580 | |
| валовый продукт | 285,6 | 331,1 | 362,8 | 979,5 |
Используем соотношение Х=(Е-А)’*У, полученное в соответствие модели Леонтьева для определения валового выпуска для этого найдем: (Е-А)’ – матрицу полных затрат (Е – единичная матрица),
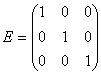

Найдем обратную матрицу (Е-А)’ используя функцию в Excel (fx/математическая/МоБР),
| 0,1706485 |
| |
| В=(Е-А)-1 | 0,1706485 | 1,2969283 | 0,2047782 |
| 0,2901024 | 0,2047782 | 1,3481229 |
![]()
![]()
![]()
![]()
![]()
![]() Найдем величины валовой продукции, используя в Excel (fx/математическая/МУМНОЖ
Найдем величины валовой продукции, используя в Excel (fx/математическая/МУМНОЖ
| 1,0750853 | 0,1706485 | 0,2901024 | * | 180 | 285, 66553 | |||
| В=(Е-А)-1*У | 0,1706485 | 1,2969283 | 0,2047782 | 200 | =331,05802 | |||
| 0,2901024 | 0,2047782 | 1,3481229 | 200 | 362,79863 |
Рассчитаем величины производственных затрат по формуле
Xij=aij*xj
aij- технологическая матрица
xj-строка валового выпуска,
Категории:
Подобное:
Copyright © https://www.referat-web.com/. All Rights Reserved |
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

