Экономический анализ характеристик взаимосвязи
Министерство образования и науки Украины
ДонГТУ
Кафедра экономической кибернетики
Контрольная работа
по предмету «Эконометрия»
Вариант № 1
Выполнил:
Ст.гр. МВД-05-1
Бурмистрова А,
Проверила:
Якимова Л.П.
Алчевск 2008
Условие задачи
По статистическим данным для 9 предприятий общественного питания за год построить линейную двухфакторную модель, которая характеризует зависимость между уровнем рентабельности (%), относительным уровнем затрат оборота (%) и трудоемкостью предприятий. Прогнозные значения факторов выбрать самостоятельно. Сделать экономический анализ характеристик взаимосвязи.
Исходные данные
| № п/п | Рентабельность | Затраты оборота | Трудоемкость |
| 1 | 2,48 | 16,8 | 117,7 |
| 2 | 2,62 | 16,9 | 97,5 |
| 3 | 2,88 | 16,1 | 113,7 |
| 4 | 2,68 | 15 | 122,3 |
| 5 | 2,52 | 18 | 102 |
| 6 | 2,74 | 17,2 | 106,7 |
| 7 | 2,56 | 17,1 | 108,5 |
| 8 | 2,68 | 16,4 | 114,3 |
| 9 | 2,55 | 16,7 | 94,3 |
Построение и анализ классической многофакторной линейной эконометрической модели
1. Спецификация модели
1.1 Идентификация переменных
Многофакторная линейная эконометрическая модель устанавливает линейную зависимость между одним показателем и несколькими факторами.
Y – рентабельность – результирующий показатель;
Х1 – затраты оборота – показатель-фактор;
Х2 – трудоемкость – показатель-фактор.
Таблица 1 – Исходные данные и элементарные превращения этих данных для оценки модели.
| № п/п | Y | X1 | X2 | Y*X1 | Y*X2 | X1*X2 | Y*Y | X1*X1 | X2*X2 |
| 1 | 2,48 | 16,8 | 117,7 | 41,664 | 291,896 | 1977,4 | 6,1504 | 282,24 | 13853,29 |
| 2 | 2,62 | 16,9 | 97,5 | 44,278 | 255,45 | 1647,8 | 6,8644 | 285,61 | 9506,25 |
| 3 | 2,88 | 16,1 | 113,7 | 46,368 | 327,456 | 1830,6 | 8,2944 | 259,21 | 12927,69 |
| 4 | 2,68 | 15 | 122,3 | 40,2 | 327,764 | 1834,5 | 7,1824 | 225 | 14957,29 |
| 5 | 2,52 | 18 | 102 | 45,36 | 257,04 | 1836 | 6,3504 | 324 | 10404 |
| 6 | 2,74 | 17,2 | 106,7 | 47,128 | 292,358 | 1835,2 | 7,5076 | 295,84 | 11384,89 |
| 7 | 2,56 | 17,1 | 108,5 | 43,776 | 277,76 | 1855,4 | 6,5536 | 292,41 | 11772,25 |
| 8 | 2,68 | 16,4 | 114,3 | 43,952 | 306,324 | 1874,5 | 7,1824 | 268,96 | 13064,49 |
| 9 | 2,55 | 16,7 | 94,3 | 42,585 | 240,465 | 1574,8 | 6,5025 | 278,89 | 8892,49 |
| ∑ | 23,71 | 150,2 | 977 | 395,311 | 2576,513 | 16266 | 62,5881 | 2512,16 | 106762,64 |
| Средн. | 2,63444 | 16,6889 | 108,555556 | 43,92344 | 286,27922 | 1807,3 | 6,9542333 | 279,129 | 11862,516 |
1.2 Оценка тесноты связи между показателем Y и факторами Х1 и Х2, а также межу факторами. (Диаграмма рассеяния).
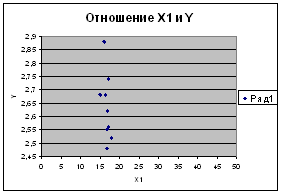
Связь тесная обратная.
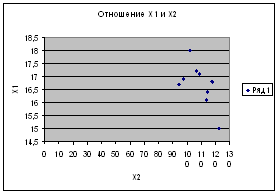
Связь обратная.
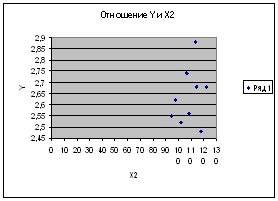
Связь тесная прямая.
| Прозноз | ||
| 1)Отношение Х1 и У | ||
| r=-0,5 | ||
| 2)Отношение Х1 и Х2 | ||
| r=-0,4 | ||
| 3)Отношение У и Х2 | ||
| r=0,5 | ||
1.2.1 Парные коэффициенты корреляции, корреляционная матрица
Для оценки тесноты связи между показателем Y и факторами Х1 и Х2, а также между факторами вычисляем парные коэффициенты корреляции, а потом составляем корреляционную матрицу, учитывая ее особенности:
- корреляционная матрица является симметричной;
- на главной диагонали размещены единицы.
Парные коэффициенты корреляции вычисляем по формулам:
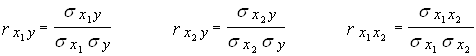
![]() - среднее квадратическое отклонение показателя Y;
- среднее квадратическое отклонение показателя Y;
![]() - среднее квадратическое отклонение фактора X1;
- среднее квадратическое отклонение фактора X1;
![]() - среднее квадратическое отклонение фактора X2;
- среднее квадратическое отклонение фактора X2;
![]() - дисперсия показателя Y;
- дисперсия показателя Y;
![]() - дисперсия показателя X1;
- дисперсия показателя X1;
![]() - дисперсия показателя X2;
- дисперсия показателя X2;
![]() - коэффициент ковариации признаков Y и Х1;
- коэффициент ковариации признаков Y и Х1;
![]() - коэффициент ковариации признаков Y и Х2;
- коэффициент ковариации признаков Y и Х2;
![]() - коэффициент ковариации признаков X1 и Х2;
- коэффициент ковариации признаков X1 и Х2;
Таблица 2 – Расчет парных коэффициентов корреляции
| По формуле | Мастер функций | ||
| Дисперсия У | Ср. кв. отклон У | Дисперсия У | Ср. кв. отклон У |
| 0,013935802 | 0,11805 | 0,013935802 | 0,11805 |
| Дисперсия Х1 | Ср. кв. отклон Х1 | Дисперсия Х1 | Ср. кв. отклон Х1 |
| 0,609876543 | 0,780945928 | 0,609876543 | 0,780945928 |
| Дисперсия Х2 | Ср. кв. отклон Х2 | Дисперсия Х2 | Ср. кв. отклон Х2 |
| 78,20691358 | 8,843467283 | 78,20691358 | 8,843467283 |
| Ковариация УХ1 | Ковариация УХ1 | ||
| -0,042506173 | -0,042506173 | ||
| Ковариация УХ2 | Ковариация УХ2 | ||
| 0,295641975 | 0,295641975 | ||
| Ковариация Х1Х2 | Ковариация Х1Х2 | ||
| -4,327160494 | -4,327160494 |
Коэффициэнты парной корреляции
| rух1 | -0,461068071 | rух1 | -0,461068 | |
| rух2 | 0,283189751 | rух2 | 0,28319 | |
| rух1х2 | -0,626555382 | rух1х2 | -0,626555 |
Корреляционная матрица
| 1 | -0,46107 | 0,28319 |
| -0,46107 | 1 | -0,62656 |
| 0,28319 | -0,62656 | 1 |
1.2.2 Коэффициенты частичной корреляции
В многомерной модели коэффициенты парной корреляции измеряют нечистую связь между факторами и показателем. Поэтому при построении двухфакторной модели целесообразно оценить связь между показателем и одним фактором при условии, что влияние другого фактора не считается. Для измерения такой чистой связи вычисляют коэффициенты частичной корреляции.
Формула частичного коэффициента корреляции между признаками Хi и Xj![]() имеет вид:
имеет вид:
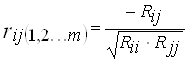
где ![]() - алгебраические дополнения соответствующих элементов корреляционной матрицы.
- алгебраические дополнения соответствующих элементов корреляционной матрицы.
Во время построения двухфакторной модели коэффициенты частичной корреляции рассчитываются по формулам:
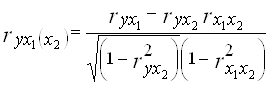
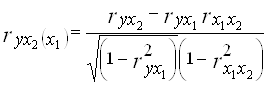
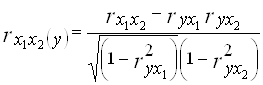
Для проверки полученных коэффициентов рассчитаем их матричным методом по формуле:

где ![]() - элементы матрицы
- элементы матрицы ![]() обратной корреляционной матрицы R.
обратной корреляционной матрицы R.
Таблица 3 – Расчеты коэффициентов частичной корреляции
| По определению | Матричный метод | ||
| ryx1(x2) | -0,3794576 | -0,379460035 | |
| ryx2(x1) | -0,0082345 | -0,010381071 | |
| rx1x2(y) | -0,7171655 | -0,734325768 | |
| Корреляционная матрица, R | Матрица, обратная корреляционной, C | |||||||
| y | x1 | x2 | ||||||
| y | 1 | -0,46107 | Подобное:
Copyright © https://referat-web.com/. All Rights Reserved | |||||
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

