Скачать

Некоторые вопросы анализа деловых проблем

Реферат выполнили студентки группы БУА-02-1 Вартанян Маргарита Александровна и Балахонова Марина Сергеевна

Северо-Кавказский горно-металлургический институт (Государственный технологический университет)

Факультет: экономический

Кафедра: математики

Владикавказ 2004

Глава I. Задача принятия решения

При рассмотрении задач исследования операций мы всегда имеем дело с количественной информацией. Но так бывает не всегда: выбор профессии, места работы, проектов научных исследований и т. д. — примеры ситуаций, когда важными являются многие качественные факторы. К этому добавляется неопределенность в исходной информации, связях факторов, последствий нашего выбора, многокритериальность оценивания альтернатив.

В силу уже только этих перечисленных факторов лицо, принимающее решения, (ЛПР) вынуждено выходить за рамки исследования операций, действовать неформально, на основе своего опыта, своей интуиции и (подчеркнем особо!) субъективно.

§ 1.1. Проблема выбора в сложных ситуациях

Принятие решений, то есть выбор одной из возможных альтернатив, — это практически постоянный атрибут человеческой жизни. Многие решения мы принимаем, не задумываясь, некоторые решения обдумываем достаточно тщательно, наконец, бывают такие решения, которые мы обдумываем чрезвычайно серьезно. Как правило, проблемы, которые надо решить в этом, последнем случае, имеют исключительный, неповторяющийся характер, связаны с целым рядом альтернатив, отличаются либо новым объектом выбора, либо новыми условиями выбора.

Для таких сложных ситуаций характерны следующие черты проблем, решение которых ищется:

• уникальность, неповторимость ситуации выбора;

•сложность оценивания рассматриваемых альтернатив;

• недостаточная определенность последствий принимаемых решений;

• наличие совокупности разнородных факторов, которые следует принимать во внимание;

• недостаточная определенность последствий принимаемых решений;

• наличие совокупности разнородных факторов, которые следует принимать во внимание;

• ответственность за принятое решение и наличие лица или группы лиц, принимающих на себя эту ответственность.

Конечно, проблема рационального выбора в сложных ситуациях была всегда, но в наше время острота этой проблемы возросла:

• возрос динамизм жизни, уменьшилось время, в течение которого принятое решение остается верным;

• развитие науки и техники привело к появлению большого числа альтернативных вариантов выбора;

• возросла сложность каждого из вариантов принимаемых решений;

• увеличилась взаимозависимость разных решений и их последствий.

Сразу надо сказать о двух существенных моментах. Первый из них — это кажущиеся проблемы. В 1946 году знаменитый немецкий физик Макс Планк прочитал доклад «Кажущиеся проблемы науки», который он начал вопросом: на какой стороне зала, где он выступает, находятся окна — справа или слева? На такой вопрос можно ответить только в том случае, если одновременно указать собственное местоположение, только в этом случае вопрос имеет смысл и допускает решение. Бывают, конечно, и более сложные случаи возникновения кажущихся проблем, для которых не хватает определенных предпосылок, граничных условий. Зачастую такие проблемы встречаются в скрытой форме, поэтому первоначально еще надо показать, что проблема существует (то есть что решение /надо искать, оно не лежит на поверхности) и что решение может быть найдено.

К кажущимся проблемам относятся и вопросы, в которых недостает подробностей, необходимой исходной информации, что не позволяет превратить их в конкретные аргументированные, сравнимые, допускающие оценивание альтернативы (это расплывчатые вопросы типа «Что требует первоочередного развития: промышленность или сельское хозяйство?»). Еще один вид кажущихся проблем — это такие проблемы, решение которых зависит от личных взглядов, вкусов, привычек, склонностей («Какой вид спорта лучше — бокс или футбол?»). Следующий вид кажущихся проблем — это проблемы, в которых просто нет выбора, а есть жесткая обусловленность обстоятельствами (лопнула шина вашего велосипеда, инструментов для ремонта нет, денег на попутный транспорт нет, остается, как пел В. Высоцкий: «...а дальше пёхом и не стонать!»).

Наконец, еще одной разновидностью кажущихся проблем являются «логические ловушки» — задачи, противоречащие логике. Примером таковой является задача о корабельном парикмахере, который по приказу капитана должен брить всех мужчин, находящихся на корабле, которые не бреются сами. Будет или не будет парикмахер брить себя, он нарушает приказ капитана.

В дальнейшем мы будем иметь дело с реальными, а не кажущимися проблемами.

Второй существенный момент состоит в следующем. Ниже будет рассказано о некоторых методах принятия решений, каждый из которых в той или иной степени формализован, представлен как свод правил действий, алгоритмов выбора. Надо иметь в виду, что метод — это инструмент и, как каждый инструмент, он может быть полезен, бесполезен, а то и вреден. Принятие решения — процесс творческий, соединение науки с искусством, и таковым он останется всегда. Рост мощности методов позволяет переходить от использования лишь здравого смысла и интуиции (которые, конечно, всегда будут необходимы при принятии решения) к созданию большего числа альтернатив и более глубокой их проработке. Безусловно, менеджеру надо быть хорошо осведомленным о существующих методах принятия решений, чтобы, с одной стороны, не превратиться из ЛПР (лица, принимающего решения) в ЛПБ (лицо, подписывающее бумаги, разработанные другими) и чтобы, с другой стороны, повысить эффективность своей работы.

§ 1.2. Разработка сценариев, построение и анализ дерева целей

Выше мы обсудили вопрос о том, почему возникает и в чем сот 'стоит проблема выбора. Сейчас вашему вниманию предлагается одна из возможных концепций действий, направленных на решение этой проблемы.

Будем исходить из того, что деятельность человека, б том числе и принятие решения, является целенаправленной. В силу этого формирование цели (целей) деятельности — это первостепенный шаг как по важности, так и по порядку действий. Поскольку цель (желаемый результат деятельности) взаимосвязана с той общей жизненной ситуацией, которая будет иметь место в момент окончания деятельности, постольку возникает вопрос о прогнозировании будущей картины мира (или региона, или какого-то сектора экономики и т. д.). Маленький, но красочный пример: пока руководители одной великой державы раскачались и закупили импортный завод по производству болоньевых плащей, мода на них прошла.

Прогнозирование будущей картины интересующей нас части мира и будущих возможных состояний в этой части мира (этой частью может быть и маленькое-маленькое предприятие) называют разработкой сценария. Разработка сценариев — высококвалифицированная, кропотливая и ответственная работа. Кроме того, эта работа — неформализуемая, творческая, для нее нет исчерпывающего алгоритма проведения.

Одной из основных задач при разработке сценария является определение факторов, которые характеризуют ситуацию и тенденции ее развития, а также определение альтернативных вариантов динамики их изменения. Разработка сценариев — широкое поле для использования экспертных методов.

Обычно перед разработкой сценария проводится анализ ситуации с определением основных действующих сил, взаимоотношений между факторами, которые существенны в данной ситуации, формируется набор существенных переменных, достаточно полно определяющих развитие анализируемой ситуации. Конечно, переменные могут быть как количественные, так и качественные. Первые позволяют получать более достоверные оценки (но не всегда!), вторые позволяют отразить действительный характер анализируемой ситуации. Количество переменных должно быть разумно необходимым, так как избыток переменных затрудняет анализ ситуации, а недостаток делает анализ поверхностным и ненадежным. Для каждой переменной выбирается своя шкала.

При разработке сценариев желательна многовариантность описания будущей ситуации. Группируя варианты сценариев в классы, можно определить рациональную стратегию воздействия на ситуацию. Несколько вариантов сценария обычно более информативны, чем один.

Для разработки сценариев привлекаются специалисты самых разных профилей. Результатом их работы, скажем, для фирмы-производителя должен быть прогноз потребности в продукции фирмы. Этот прогноз является, конечно, главной частью сценария, но не единственной. Необходим прогноз предельных возможностей смежников по развитию производства и поставок; прогноз жизненного цикла изделий; прогноз поведения конкурентов; прогноз новых возможностей, обусловленных научно-техническим прогрессом; иногда нужна оценка запасов природных ресурсов и предельных возможностей объемов их добычи и т. д. Ясно, что круг вопросов, включаемых в рассмотрение при разработке сценария, связан с желаниями, с формулируемыми целями. Цели и сценарий в определенной мере взаимосвязаны. Конечно, сценарий не имеет ценности, если он является результатом поверхностного теоретизирования («Рассчитали на бумаге, да забыли про овраги, а по ним ходить...»).

Желания и сценарий являются основой формирования не только главной, генеральной цели (или нескольких взаимно независимых целей), но и целого дерева целей, в котором достижение цели или группы целей данного уровня является необходимым условием для возможности достигнуть цель следующего, вышележащего уровня. По мере перехода к нижележащим уровням (возможно, уже при переходе ко второму уровню) начинается формирование каких-то конкретных задач и заданий.

В качестве примера назовем дерево целей НАСА (Национальной администрации по аэронавтике и исследованию космического пространства, США), которое было в свое время (1965 год) таким:

Первый уровень — цели: изучение космоса; использование космоса.

Второй уровень — задачи: изучение Солнца и планет Солнечной системы; исследование глубокого вакуума, радиации и других условий космоса и т. д. (всего 15 элементов).

Третий уровень — задания, обеспечивающие решение задач, второго уровня: всестороннее изучение Луны; развитие средств связи и навигации; изучение биологических аспектов и т. д. (всего 68 элементов).

Четвертый уровень — принципиальные опыты. Проведение этих опытов обеспечивало решение задач предшествующих уровней (всего 31 опыт).

Пятый уровень — системы: системы запуска космических кораблей; космические корабли для облета планет человеком; системы для высадки людей и т. д. (оказалось достаточным 46 систем).

Шестой уровень — подсистемы: аппаратура, необходимая для достижения системами их конечных целей (бортовые источники энергии; средства обработки данных и т. д., всего 437 элементов).

Седьмой уровень — функциональные элементы, составляющие в целом какую-то подсистему: например, бортовые источники энергии — это собственно источники энергии, преобразователи энергии из одного вида в другой, устройства накопления энергии и регулирования ее расхода и т. д. (всего 274 наименования)

Восьмой уровень — конструктивные варианты подсистем: различные способы технической реализации функциональных элементов (всего 804 элемента).

Наконец, девятый уровень — технические проблемы, связанные с преодолением каких-то научных или инженерных трудностей (всего 2329 элементов).

Можно было бы ограничиться менее масштабным примером, но приведенный пример, думается, лучше иллюстрирует процесс разворачивания дерева целей, в котором полно, последовательно, в логической взаимосвязи строится остов последующей работы по планированию и управлению.

При построении дерева целей сверху вниз, исходя из главной цели, открывается возможность согласования затрат, сбалансированного распределения ресурсов. Достоинством рассматриваемой концепции является также то, что нижележащие уровни выдвигают свои предложения в соответствии с теми целями, достижение которых необходимо для достижения главной цели, а не исходя из достигнутого ими уровня и их сиюминутных желаний, связанных с их собственным развитием.

Наконец, достоинство дерева целей в том, что оно позволяет если не исключить, то хотя бы сократить пропуски и ошибки в планировании. На основе дерева целей с использованием определенных методов экспертного оценивания оказывается возможным количественное соизмерение элементов дерева с помощью коэффициентов их относительной важности, которые выражают меру необходимости проведения того или иного мероприятия. Кроме только что названных величин, с помощью экспертизы по дереву целей можно оценивать возможные сроки завершения работ, а также экономические затраты, необходимые для этого. Наконец, дерево целей позволяет формально и достаточно точно оценить коэффициенты взаимной полезности, то есть увеличение научно-технического потенциала, который может быть использован при работе по решению данной задачи, за счет знаний, накопленных при решении какой-то другой задачи (или других задач).

Мы не будем сейчас рассматривать методы экспертного оценивания, с помощью которых находят названные характеристики, поскольку раньше об экспертизе уже было рассказано довольно подробно. Сэкономив на повторении в данном пункте, мы лучше кратко рассмотрим некоторые еще не встречавшиеся нам подходы к решению проблемы выбора (новые по сравнению с теми, о которых шла речь в разделе, посвященном исследованию операций).

Глава II. Некоторые методы анализа деловых проблем

§ 2.1. Подходы к решению проблемы выбора

Каждая проблема принятия решения имеет свои особенности, но у всех проблем есть и общие компоненты:

• наличие какой-то определенной, своей в разных случаях, исходной ситуации;

• не менее двух вариантов решения;

• последствия при выборе каждого из вариантов.

Можно выделить и общий подход к решению проблемы выбора:

• исследовать собственно проблему;

• уяснить исходную ситуацию;

• сформировать возможные решения;

• описать последствия этих решений;

• оценить возможные варианты решений и последствия решений;

• выбрать решения;

• обобщить опыт принятия решений.

Эта общая схема конкретизируется в соответствии с характером задачи. Если по своей сути перед нами задача исследования операций (о чем шла речь в части I), то можно назвать следующие логические элементы:

• выделение цели или совокупности целей;

• выделение альтернативных средств, при помощи которых можно достичь цели;

• определение необходимых ресурсных затрат для каждой альтернативы;

• построение математической или логической модели, то есть определение зависимости между целями, альтернативными средствами их достижения, окружающей средой и ресурсами;

• определение критерия выбора предпочтительной альтернативы;

• проведение необходимых расчетов, их анализ, внесение, при необходимости, соответствующих коррективов;

• собственно принятие решения и его исполнение.

Если задачей является принятие решений в организации, то можно выделить следующие этапы:

• определение целей деятельности организации;

• выявление проблем, трудностей в процессе достижения этих целей;

• исследование проблем и постановка диагноза;

• поиск альтернатив решения, оценка альтернатив, выбор лучшей;

• согласование решений в организации и их утверждение;

• подготовка к вводу решения в действие;

• управление осуществлением решения;

• проверка эффективности принятого решения, внесение необходимых коррективов.

Общими в подходе к решению проблемы выбора являются и следующие пять аспектов:

• КТО должен (или хочет) решать?

• ГДЕ, то есть на каком месте, в каком окружении, при каких обстоятельствах и граничных условиях предстоит принять решение?

• КОГДА (до какого срока или как часто) надо принимать решение?

• КАК (каким образом или в какой форме) должно быть выражено решение?

• ЧТО обуславливает решение? В чем его цель?

• ДЛЯ ЧЕГО оно служит? Зачем его надо принимать?

Наконец, надо заметить, что обсуждение процесса разработки и принятия решения — это фактически тоже моделирование. При таком моделировании, конечно, надо следовать определенным принципам. К моделям принятия решений предъявляют следующие требования:

• корректность (математическая и формально-логическая непротиворечивость модели, невозможность получения в ее рамках бессмысленных, принципиально невозможных или противоречащих друг другу результатов);

• адекватность (правильность отражения в модели моделируемых принципов и особенностей процесса принятия решения);

• полнота (достаточная точность и достаточный объем отражения основных принципов, лежащих в основе принятия решения);

• универсальность (возможность ее применения к достаточно широкому классу ситуаций).

Теперь давайте познакомимся с некоторыми процедурами выбора. Прежде всего отметим, что при использовании любой из них, важно не только сопоставить все возможные решения, но и иметь как можно более полный перечень возможных решений. Самая хорошая процедура, используемая самым хорошим менеджером, не даст того варианта решения, который не попал в поле зрения, не пришел на ум (фокусник не может вынуть из своей шляпы того, что туда не было положено).

По-видимому, самая простая процедура выбора изображена на рис. 2.1.

Рис, 2.1. Схема возможных вариантов

Возможные варианты довольно легко приходят в голову, хорошо группируются, анализируются и оцениваются. Более подробное и более объемное представление проблемы дает целое дерево решений, о чем будет идти речь дальше.

Достаточно широко используется процедура, известная под названием «морфологический анализ», или «морфологический метод». Несколько упрощая суть этого метода, можно представить его так. Составляется таблица, в левой колонке которой могут быть перечислены, скажем, объекты воздействия, а в верхней строке — возможные способы воздействия (мероприятия). Затем клетки заполняются возможными воздействиями на данный объект какими-либо вариантами данного способа. Достоинство метода в том, что можно целенаправленно формировать как объекты воздействия, так и способы воздействия, а затем систематически исследовать различные варианты. Приведем в качестве примера морфологическую таблицу для торговой фирмы, желающей увеличить сбыт и уменьшить расходы (пример, конечно, максимально упрощенный) (табл. 2.1).

Таблица 2.1. Упрощенный вид морфологической таблицы

В рамках морфологического анализа можно рассматривать и задачи с достаточно большим числом варьируемых переменных, (то есть не только те две переменные, объект — способ воздействия, о которых написано раньше).

Широкое применение в настоящее время получили специальные математические методы, используемые в сложных и объемных (с большим числом учитываемых факторов) ситуациях. В качестве примера опишем метод «Стоимость — эффективность».

Допустим, решается вопрос об определении количества рекламных щитов с информацией о товарах вашей фирмы. С помощью экспертов или из статистических данных можно оценить (и довольно точно!) связь объемов продаж с количеством щитов. С другой стороны, можно подсчитать (достаточно точно!) общие затраты как функцию числа щитов. Эта функция может расти нелинейно, так как при изготовлении большего числа щитов может возникнуть экономия (на накладных и транспортных расходах, скидка при оптовых закупках и т. д.). Затем ЛПР совместно анализирует связь эффективности рекламы и ее стоимости. В простейшем случае можно ориентироваться на отношение стоимости к результату, то есть на отношение затрат на рекламу к доходу от продаж. Можно сравнивать дополнительные затраты на рекламу с дополнительным доходом, который приносит эта реклама. Иногда ЛПР фиксирует определенную желательную эффективность и минимизирует затраты или, наоборот, задается бюджетным ограничением на затраты и стремится максимизировать эффективность.

Как понятно из приведенного примера, метод «Стоимость — эффективность» — это оптимизационный подход к достаточно объемным или громоздким задачам, а также к задачам, в которых есть трудности с представлением исходной информации (о такой ситуации речь будет идти в следующем пункте).

Как правило, умелое сочетание науки, математических методов и искусства менеджера дает хорошие результаты при использовании подхода «Стоимость — эффективность».

§ 2.2. Поиск решений в расплывчатых условиях

Для формализованного описания реальных ситуаций, в которых нет полной определенности и однозначности, сейчас используется такой математический аппарат, как теория нечетких множеств.

Термин "fuzzy sets", введенный Л. Заде, переводится по-разному: размытые, нечеткие, нечетко определенные, расплывчатые и т. д. множества. С использованием этого термина был дан ряд определений и введены понятия, на основе которых построен новый математический аппарат. Одной из областей применения этого аппарата является теория принятия решений.

Математический аппарат нечетких множеств достаточно сложен (во всяком случае достаточно необычен); большого распространения и применения нечеткие множества еще пока не получили; по-видимому, теория нечетких множеств пока далеко не на таком уровне кристаллизации и завершенности, как классические разделы высшей математики (это, бесспорно, положительное качество для исследователя, но сомнительное достоинство для студента). Но есть мотивы, в силу которых кратко, на описательном уровне ниже рассказывается о применении теории нечетких множеств при принятии решений:

• методы этой теории хорошо соотносятся с образом человеческого мышления, и знакомство с нечеткими множествами позволяет, с одной стороны, более осознанно и более эффективно разрабатывать и принимать решения, а с другой стороны, способствует формированию правильной профессиональной психологии;

• ясно, что со временем теория нечетких множеств будет иметь более широкое распространение, чем сейчас, поэтому первое знакомство с ней откладывать не стоит (уже есть сообщения о том, что с использованием методов этой теории получены технические решения, реализованные в высококачественной видео- и фотоаппаратуре).

Естественно, рассмотрение материала должно начинаться с определения основного понятия — понятия расплывчатого (нечеткого) множества.

Пусть Х = {х} — совокупность объектов, обозначенных через х. Расплывчатое множество А в X есть совокупность упорядоченных пар А = {х, µа (х)}, х Є X, µа (х) — степень принадлежности х множеству А, то есть µа (х) — это функция, ставящая каждому элементу х из X в соответствие какое-то (одно) число из отрезка (0; 1).

Обычное множество — это множество, для которого ц равно либо нулю, либо единице, скажем, множество четных чисел. Примером нечеткого множества может быть множество А «несколько чисел» для множества X = {0; 1; 2;...} всех неотрицательных чисел.

А = {(1; 0,0), (2; 0,05), (3; 0,2), (4; 0,6), (5; 0,8), (6; 1,0), (7; 1,0), (8; 0,8), (9; 0,6), (10; 0,2), (11; 0,05), (12; 0,0)}.

В данном примере утверждается, что одно число еще не может, а 12 чисел уже могут попадать в множество «нескольких чисел», два числа и одиннадцать чисел лишь при очень большом желании, образно говоря, могут быть охарактеризованы как несколько чисел, 6 или 7 чисел признаются таким количеством чисел, которые в данном контексте, бесспорно, отнесены автором примера к числу объектов, обладающих определенным свойством, и т. д.

Рассмотрим еще один пример, иллюстрирующий, как используются нечеткие множества. Пусть примерно прямая линия АБ — это любая линия, проходящая через точки А и Б так, что расстояние d, от каждой точки АБ до («истинной») прямой (АБ)° по отношению к длине (АБ)° мало, d — нечеткая переменная (читатель может сам определить d). Примерно средней точкой М на АБ назовем такую точку, расстояние от которой до М° — середины (АБ)° — мало.

С использованием приведенных понятий можно для известной теоремы о трех медианах треугольника (три медианы треугольника пересекаются в одной точке) сформулировать аналог — нечеткую теорему. Пусть АВС — примерно равносторонний треугольник с вершинами А, В, С, а М1, М2, М3 — примерно середины сторон ВС, АС, АВ.

Тогда примерно прямые АМ1, ВМ2, СМз образуют «примерно» треугольник Т1Т2T3, который более или менее мал в сравнении с треугольником АВС (рис. 2.2).

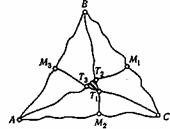
Рис. 2.2. Нечеткая теорема о трех «медианах»

Конечно, приведенные примеры скорее забавны, чем практически полезны, но дело в том, что мы постоянно пользуемся нечеткими понятиями, рассуждениями, множествами, теоремами:

• у корпорации X прекрасные перспективы;

• на фондовой бирже наблюдается резкий спад;

• корпорация У использует прогрессивную технологию и т. д.

Обратите внимание на то, что для описания расплывчатости недостаточно теории вероятностей и статистических методов, они предназначены для работы со случайностью, когда речь идет о принадлежности некоторого объекта к четкому множеству. Скажем, последний из приведенных примеров содержит расплывчатое утверждение вследствие неточности, нечеткости выражения «прогрессивная технология», в то время как утверждение «вероятность того, что фирма 2 работает в убыток, равна 0,8» содержит информацию о мере неопределенности относительно принадлежности 2 к четкому множеству фирм, работающих в убыток.

Люди, в отличие от ЭВМ, обладают способностями оперировать расплывчатыми понятиями и выполнять расплывчатые инструкции (вспомните русскую народную сказку, в которой герой блестяще выполнил одну из таких инструкций: «Пойди туда, не знаю куда, принеси то, не знаю что»). Люди также способны на интуитивном уровне оперировать с расплывчатыми целями («Фирме надо сохранить за собой около 15—20% рынка»), расплывчатыми ограничениями («Фирма не может потратить на рекламу значительную часть квартального дохода») и с расплывчатыми решениями («На рекламу будет выделено около 5—8% дохода»).

При том подходе к принятию решений в расплывчатых условиях, который развит Р. Беллманом и Л. Заде, и цель, и ограничения рассматриваются как расплывчатые множества в пространстве альтернатив.

Если X = {х} — заданное множество альтернатив, то расплывчатая цель Q отождествляется с фиксированным расплывчатым множеством Q в X. Например, если X — действительная прямая, а расплывчатая цель формулируется как «х должно быть значительно больше 10» (скажем, доход должен быть таким в каких-то известных единицах), то эту цель можно представить как расплывчатое множество с функцией принадлежности

Расплывчатое ограничение С в пространстве X определяется таким же образом, то есть как некоторое расплывчатое множество в X. Если, как и для цели, X — действительная прямая, то ограничение «х должно быть приблизительно в окрестности 15» (такими могут быть ограничения на затраты) представимо с помощью функции принадлежности

Если в пространстве альтернатив X заданы расплывчатая цель Q и расплывчатое ограничение С, то расплывчатое множество D, образованное пересечением Q и С, называется расплывчатым решением. В специальных работах показано, что для D = Q П С,

будет

В условиях приводимых выше примеров

Взаимосвязь расплывчатых цели, ограничений и решения показана на рис, 2,3.

В том случае, когда расплывчатая цель Q задана в множестве У = {у}, а ограничение — в множестве X = {х}, причем х — причина, у — следствие и есть отображение f множества из X в У, можно для Q из У найти в X множество Q, порождающее Q. Функция принадлежности Q задается равенством µQ (х) =µQ (f(х)).

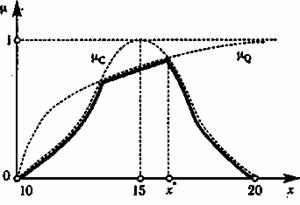
Рис.2.3. Нахождение расплывчатого решения

(µd — сплошная линия на рисунке, который несколько деформирован по сравнению с истинным для большей наглядности;

х' — оптимальное решение)

Решение в этом случае ищется, как и раньше, в виде пересечения Q и С:

Так, в простейшем случае используются нечеткие величины при принятии решений.

В силу очевидных причин затронутые вопросы в большей мере сейчас не рассматриваются. Будем надеяться, что изложенный материал, пользуясь терминологией данного пункта, будет для вас, читатель, «достаточно полезен».

§ 2.3. Поиск решений при наличии многокритериальных альтернатив

В разделе, посвященном исследованию операций, коротко было рассказано о многокритериальных оптимизационных задачах. Этот рассказ, касающийся математических аспектов ситуаций, когда имеется несколько критериев, — необходимая часть сведений, которыми должен быть вооружен менеджер, но только часть сведений, касающихся принятия решений при большом числе альтернативных вариантов выбора и значительном числе разнородных критериев, когда ЛПР не может, вообще говоря, в одиночку, самостоятельно составить целостную картину качества альтернативных вариантов. Есть различные методы организации деятельности ЛПР в таких условиях, ни один из них не претендует на универсальность. Из-за ограниченности объема данного пособия мы обсудим только один из возможных подходов, позволяющий учесть специфику получения информации от ЛПР и экспертов, которые в подобной ситуации крайне необходимы.

Перечислим основные положения, которые должны учитываться при построении многокритериальных моделей задач принятия решений:

• модель создается исследователем для структуризации и уточнения предпочтений лица, принимающего решения, которое непосредственно участвует в ее разработке;

• модель должна быть логически непротиворечива;

• модель должна содержать описание всех возможных элементов задачи принятия решений и свойства этих элементов;

• модель должна давать возможность использовать реальную информацию о задаче, полученную от экспертов, ЛПР;

• модель должна быть достаточно простой и удобной для анализа и использования ЛПР.

Под критериями понимают такие показатели, которые:

• признаются ЛПР в качестве характеристик степени достижения поставленной цели;

• являются общими и измеримыми для всех допустимых решений;

• характеризуют общую ценность решений таким образом, что у ЛПР имеется стремление получать по ним наиболее предпочтительные оценки (то есть в качестве критериев не следует использовать ограничения).

Набор критериев многокритериальной задачи должен удовлетворять следующим требованиям:

• полнота (использование любых дополнительных критериев не меняет результатов решения, а отбрасывание хотя бы одного из выбранных критериев меняет результат);

• операциональность (каждый критерий должен иметь понятную для ЛПР формулировку, ясный и однозначный смысл, характеризовать определенный аспект решения);

• декомпозируемость (набор критериев должен позволять упрощать оценивание предпочтений путем разбиения первоначальной задачи на отдельные более простые подзадачи);

• неизбыточность (разные критерии не должны учитывать один и тот же аспект решения);

• минимальность (аспект решения должен содержать как можно меньшее число критериев);

• измеримость (каждый критерий должен допускать возможность количественной или качественной оценки степени достижения соответствующей цели).

Эти требования, конечно, противоречивы, но ясное представление о них позволяет строить полноценный набор критериев.

Частные и типичные пробелы в анализе многокритериальных задач принятия решений:

• нет полного списка допустимых вариантов решений;

• нет полного списка критериев, характеризующих качество решений;

• не построены все или некоторые шкалы критериев;

• нет оценок вариантов решений по шкалам критериев;

• нет решающего правила, позволяющего получить требуемое в задаче упорядочение вариантов решения (решающее правило, метод принятия решения, представляет собой принцип сравнения векторных оценок и формирования суждения о предпочтительности одних из них по отношению к другим).

Известно, что возможности человека по переработке многомерной информации очень ограничены, поэтому вероятность ошибочных действий ЛПР достаточно велика. В рамках рассматриваемого подхода были предложены два варианта проверки действий ЛПР.

Первый — критерий непротиворечивости: в аналогичных ситуациях оценки или сравнения альтернатив руководитель должен принимать одинаковые решения. Конечно, предпочтения ЛПР могут меняться во времени, но не таким образом, чтобы эти изменения служили иллюстрацией броуновского движения (согласитесь, логично ожидать непротиворечивого поведения от человека во время получения от него деловой информации). Этот критерий основан на предположении о существовании у ЛПР определенной, непротиворечивой политики. Отметим, что при всей естественности такого предположения, при всей очевидной его справедливости в реальных ситуациях так бывает не всегда.

Второй критерий для оценки деятельности ЛПР — критерий транзитивности, который для трех альтернатив А, В, С можно записать так:

Если А > В, В > С, то А > С (для отношения предпочтения);

Если А = В, В = С, то А = С (для отношения безразличия).

При нарушении транзитивности возникает порочный круг типа А > В, В > С, С > А и выделить предпочтительный вариант невозможно.

Как и в случае с первым критерием, надо сказать, что в реальных ситуациях появление нетранзитивности в предпочтениях ЛПР вполне возможно.

В специальной литературе обсуждаются как причины появления противоречивости и нетранзитивности, так и способы выхода из этих достаточно сложных ситуаций. Здесь же отметим, что для ЛПР имеет смысл сознательно избегать нарушения указанных критериев.

Известно, что для человека сложными являются задачи с большой нагрузкой на понятийный аппарат; задачи, требующие параллельной обработки многомерной информации; сравнение альтернатив с малыми уровнями различимости; задачи, имеющие значительное число критериев (5—6—7 и больше), значительное число оценок на шкалах критериев (5 и больше), значительное число результирующих классов решений (5—6 и больше).

Характерными для такого подхода, о котором сейчас идет речь, являются следующие особенности. Для описания ситуаций приня тия решения используется естественный язык данной организации: понятия «хуже» и «лучше» для каждого критерия формулируются в виде развернутых словесных определений. При сборе информации используются лишь такие вопросы, для которых заранее была установлена возможность получения надежных, непротиворечивых ответов. На основе опыта и интуиции ЛПР определены общие правила оценки альтернативных вариантов, определен перечень критериев оценивания.

Во многих случаях целесообразно использовать шкалы качественных критериев со