Скачать

Существование решения дифференциального уравнения и последовательные приближения

Курсовая работа

Выполнил студент 2 курса 1222 группы Труфанов Александр Николаевич

Государственное образовательное учреждение высшего профессионального образования «Самарский государственный университет»

Механико-математический факультет

Кафедра дифференциальных уравнений и теории управления

Самара 2004

Теорема существования и единственности решения уравнения

Пусть дано уравнение

с начальным условием

Пусть в замкнутой области R функции и непрерывны). Тогда на некотором отрезке существует единственное решение, удовлетворяющее начальному условию .

Последовательные приближения определяются формулами:

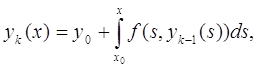k = 1,2....

Задание №9

Перейти от уравнения

к системе нормального вида и при начальных условиях

, ,

построить два последовательных приближения к решению.

Произведем замену переменных

;

и перейдем к системе нормального вида:

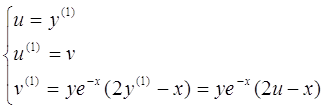
Построим последовательные приближения

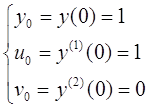
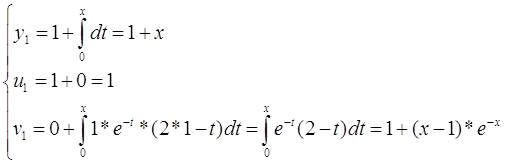
Задание №10

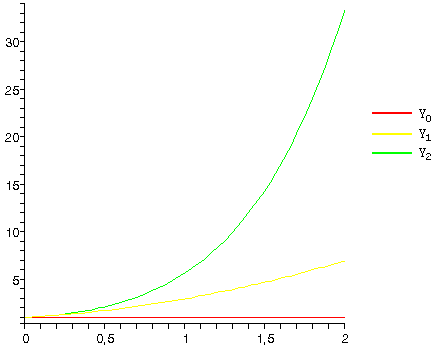
Построить три последовательных приближения к решению задачи

,

Построим последовательные приближения

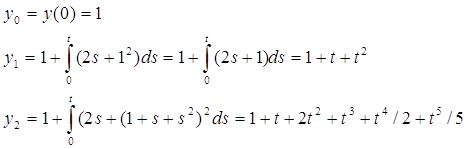
Задание №11

а) Задачу

,

свести к интегральному уравнению и построить последовательные приближения

б) Указать какой-либо отрезок, на котором сходятся последовательные приближения, и доказать их равномерную сходимость.

Сведем данное уравнение к интегральному :

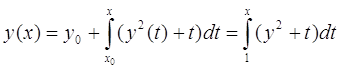
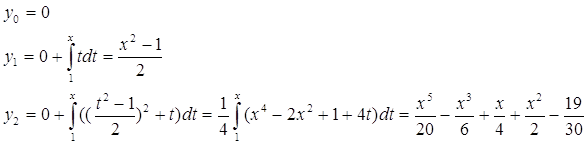
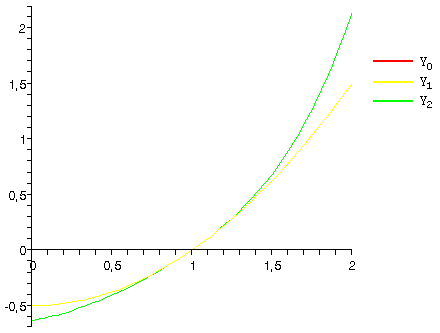
Докажем равномерную сходимость последовательных приближений

С помощью метода последовательных приближений мы можем построить последовательность

непрерывных функций, определенных на некотором отрезке , который содержит внутри себя точку . Каждая функция последовательности определяется через предыдущую при помощи равенства

i = 0, 1, 2 …

Если график функции проходит в области Г, то функция определена этим равенством, но для того, чтобы могла быть определена следующая функция , нужно, чтобы и график функции проходил в области Г. Этого удается достичь, выбрав отрезок достаточно коротким. Далее, за счет уменьшения длины отрезка , можно достичь того, чтобы для последовательности выполнялись неравенства:

, i = 1, 2, …,

где 0 < k < 1. Из этих неравенств вытекает следующее:

, i = 1, 2, …,

Рассмотрим нашу функцию на достаточно малом отрезке, содержащим , например, на . На этом промежутке все последовательные приближения являются непрерывными функциями. Очевидно, что т.к. каждое приближение представляет из себя функцию от бесконечно малого более высокого порядка, чем предыдущее приближение, то выполняются и описанные выше неравенства. Из этих неравенств следует:

что и является условием равномерной сходимости последовательных приближений.

С другой стороны, на нашем отрезке выполняется 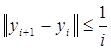, что также совершенно очевидно. А так как последовательность сходится, то последовательность приближений является равномерно сходящийся на этом отрезке.

Л.С. Понтрягин. «Обыкновенные дифференциальные уравнения», М.: Государственное издательство физико-математической литературы, 1961

А.Ф. Филиппов «Сборник задач по дифференциальным уравнениям», М.: Интеграл-Пресс, 1998

О.П. Филатов «Лекции по обыкновенным дифференциальным уравнениям»,Самара: Издательство «Самарский университет», 1999

А.Н. Тихонов, А.Б. Васильева «Дифференциальные уравнения», М.: Наука. Физматлит, 1998