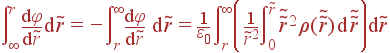Уравнение Пуассона. Его применение для расчета полей в вакууме
М.И. Векслер, Г.Г. Зегря
Уравнение Пуассона для ε = 1 выглядит:
| (16) |
Это уравнение - основа практических численных расчетов.
В задачах, решаемых аналитически, φ и ρ обычно зависят только от одной координаты. При интегрировании можно вычислять интегралы как неопределенные, не забывая выписывать +const, а затем отдельно находить эти константы. Если раccматриваются отдельные диапазоны координат, то на незаряженных границах необходимо "сшивать" потенциал: φ и - для вакуума - d φ/dx (или dφ/dr) не должны иметь разрыва. Если граница заряжена (σ), то dφ/dx испытывает скачок на величину –σ/ε0. Кроме того, если ρ и суммарный заряд конечны, то φ всюду конечен.
Другой вариант - сразу правильно писать пределы интегрирования. Для этого используется известное (или очевидное из симметрии задачи) значение поля (![]() ) в одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно в той же, где знаем поле). Если в задаче не оговорено иное, то следует принимать φ|∞ = 0. Так, например, для случая зависимости потенциала только от одной сферической координаты r
) в одной какой-либо точке и значение потенциала в какой-либо точке (не обязательно в той же, где знаем поле). Если в задаче не оговорено иное, то следует принимать φ|∞ = 0. Так, например, для случая зависимости потенциала только от одной сферической координаты r
| (17) |
после переноса r2 в правую часть и двух последовательных интегрирований получаем:
| = |
| (18) |
| φ(r) | = |
| (19) |
При этом взято φ|r = ∞ = 0 и учтено то обстоятельство, что при всюду конечном ρ поле в центре равно нулю (–dφ/dr|r = 0 = 0).
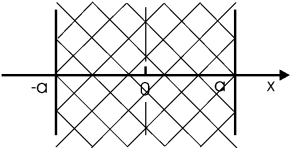
Задача. Пластина ширины 2a (ее ε≈ 1) заряжена равномерно по объему (ρ(x) = ρ0); при x = 0 (центр пластины) φ = 0. Найти φ(x).
Ответ: ![]() , |x|
, |x|
|
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Теоремы Силова
- Экономико-статистический анализ производительности и оплаты труда в ОАО "Бурятмясопром"
ВведениеПроизводительность труда характеризует способность работника произвести за единицу времени определенное количество товаров
- Методы и способы решения задач
СодержаниеЗадание 1Задание 2Задание 3Задание 4Задание 5Список использованной литературыЗадание 1Опишите понятия «задача» и процесс реш
- Тривимірні перетворення
- Некоторые замечательные кривые
В данной работе мы рассмотрим некоторые замечательные кривые и их особенности.В параграфе 1 будет рассмотрена строфоида, особенности е
- Оценка периметра многоугольника заданного диаметра
В жизни постоянно приходиться сталкиваться с необходимостью принять наилучшее возможное (оптимальное) решение. При этом часто случает
- Симплексний метод лінійного програмування
Завдання 1Кондитерська фабрика для виробництва трьох видів карамелі А1, А2, А3 використовує три види сировини: цукор-пісок, патоку і фрук
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.