Скачать

Тривимірні перетворення

Вступ

Для кращого сприйняття форми об'єкта необхідно мати його зображення в тривимірному просторі. У багатьох випадках наочне представлення про об'єкт можна одержати шляхом виконання операцій обертання і переносу, а також побудови проекцій. Введемо однорідні координати. Точка в тривимірному просторі  задається чотиримірним вектором  чи . Перетворення з однорідних координат описується співвідношеннями

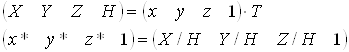(4.1)

де T - деяка матриця перетворення.

Ця матриця може бути представлена у вигляді 4 окремих частин

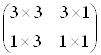
Матриця 3x3 здійснює лінійне перетворення у виді зміни масштабу, зсуву й обертання. Матриця-рядок 1х3 робить перенос, а матриця-стовпець 3х1 - перетворення в перспективі. Останній скалярний елемент виконує загальну зміну масштабу. Повне перетворення, отримане шляхом впливу на вектор положення матрицею 4x4 і нормалізації перетвореного вектора, будемо називати білінійним перетворенням. Воно забезпечує виконання комплексу операцій зсуву, часткової зміни масштабу, обертання, відображення, переносу, а також зміни масштабу зображення в цілому.

Тривимірна зміна масштабу

Діагональні елементи основної матриці перетворення 4х4 здійснюють часткову і повну зміну масштабу. Розглянемо перетворення

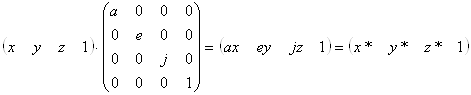,(4.2)

яке робить часткову зміну масштабу. На рис.4.1а показане перетворення паралелепіпеда в одиничний куб шляхом зміни масштабу. Загальна зміна масштабу виходить за рахунок використання четвертого діагонального елемента, тобто

.          (4.3)

Це перетворення ілюструє рис.4.1б. Такий же результат можна отримати при рівних коефіцієнтах часткових змін масштабів. У цьому випадку матриця перетворення повинна бути рівна

.                                    (4.4)

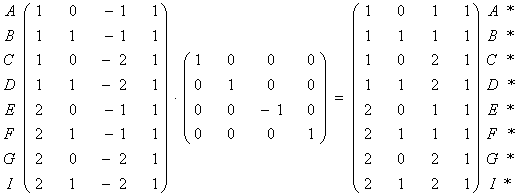
Вектори положення точок А і В рівні  і .

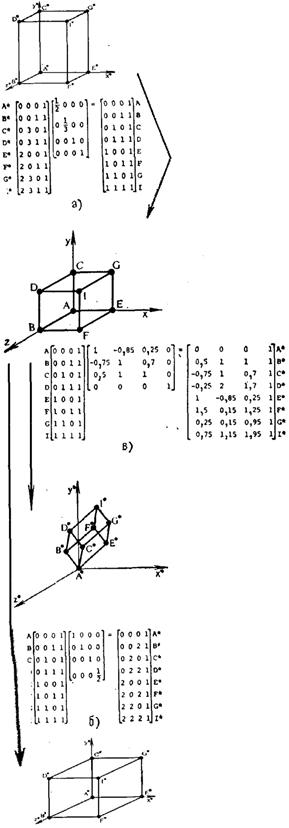
Рис.4.1. Тривимірні перетворення iз зміною масштабів.

Тривимірний зсув

Недіагональні елементи верхньої лівої підматриці 3х3 від загальної матриці перетворення розміру 4х4 здійснюють зсуви в трьох вимірах, тобто

.                       (4.5)

Простий тривимірний зсув одиничного куба показаний на рис.4.1в.

Тривимірні обертання

Раніше було показано, що матриця 3х3 забезпечувала комбінацію операцій зміни масштабу і зсуву. Однак, якщо визначник матриці 3х3 дорівнює +1, то має місце чисте обертання навколо початку координат. Перед розглядом загального випадку тривимірного обертання навколо довільної осі дослідимо кілька окремих випадків. При обертанні навколо осі х розміри уздовж осі х не змінюються. Таким чином, матриця перетворень буде мати нулі в першому рядку і першому стовпці, за винятком одиниці на головній діагоналі. Це приводить до матриці перетворення, що відповідає повороту на кут  навколо осі х і задається співвідношенням

(4.6)

Обертання вважається додатнім, тобто за годинниковою стрілкою, якщо дивитися з початку координат вздовж осі обертання. На рис.4.2а показаний поворот на -90° навколо осі x.

Для обертання на кут Ф навколо осі y - нулі ставлять у другому рядку і другому стовпці матриці перетворення, за винятком одиниці на головній діагоналі. Повна матриця задається виразом

(4.7)

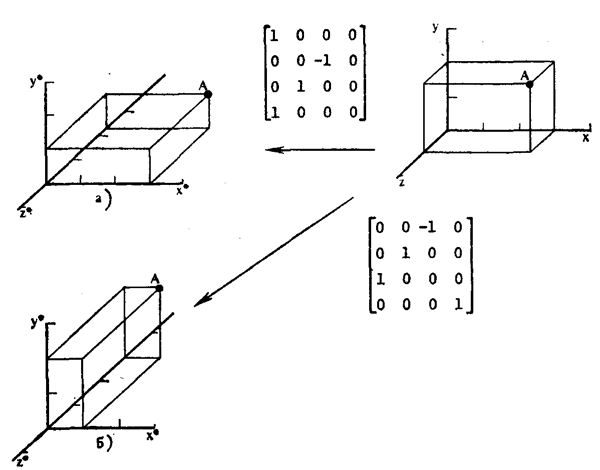
Рис.4.2. Тривимірні обертання.

На рис.4.2б показаний поворот на 90° навколо осі y. Аналогічно матриця перетворення для обертання на кут  навколо осі z має вид

(4.8)

Аналіз визначників для матриць (4.6)-(4.8) показує, що для будь-якої матриці обертання детермінант дорівнює +1.

Тому що обертання описуються множенням матриць, то тривимірні обертання некомутативні, тобто порядок множення буде впливати на кінцевий результат. Для того щоб показати це, розглянемо обертання навколо осі х, за яким слідує обертання на такий же кут навколо осі y. Використовуючи рівняння (4.6) і (4.7) при = Ф, одержимо

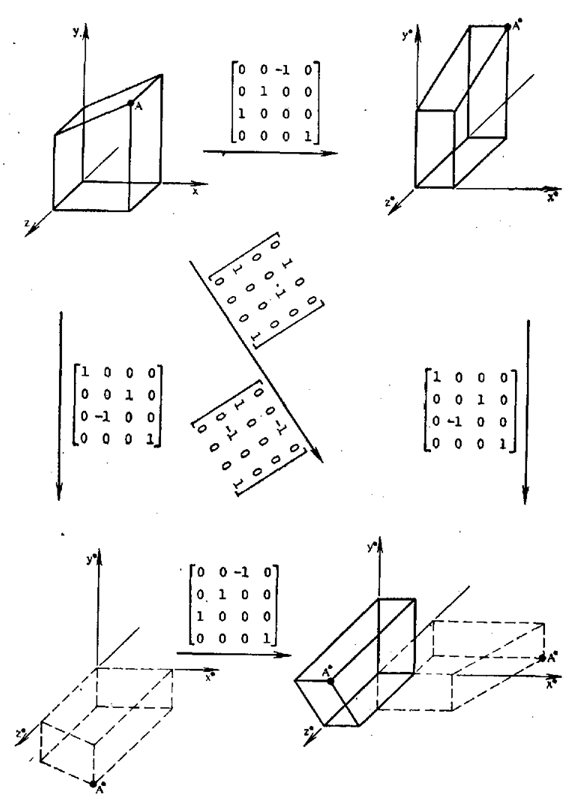
Рис.4.3. Некомутативність тривимірних обертань.

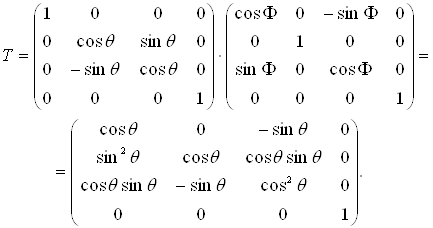(4.9)

Зворотна послідовність дій, тобто обертання навколо осі y і наступне за ним обертання на такий же кут навколо осі x при = Ф дає

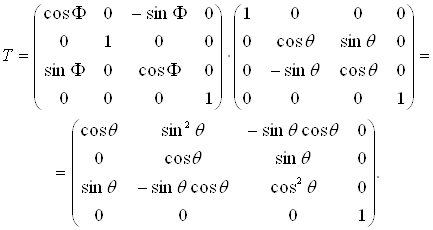(4.10)

На рис.4.3 для лівого верхнього зображення штриховими лініями показані результати двох послідовних обертань, описаних матрицею перетворення (4.9). Зображення, отримане обертаннями, виконаними в іншій послідовності, описаними рівняннями (4.10), показані суцільною лінією. З порівняння отриманих зображень видно, що при зміні порядку обертання виходять різні результати.

Часто буває необхідно обертати зображення навколо однієї з осей декартової системи координат.

Відображення в просторі

Іноді потрібно виконати дзеркальне відображення тривимірного зображення. У трьох вимірах найпростіше відображення здійснюється щодо площини. Для відображення без зміни масштабів необхідно, щоб визначник перетворення дорівнював -1,0. При відображенні щодо площини xy змінюється тільки знак координати z. Отже, матриця перетворення для відображення щодо площини xy має вигляд

(4.11)

Відображення одиничного куба щодо площини ху показане на рис.4.4. Для відображення щодо площини уz

(4.12)

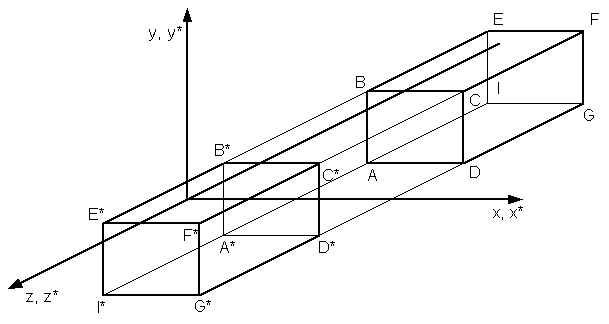
Рис.4.4. Просторове відображення щодо площини xy.

(4.12)

а для відображення щодо площини xz

(4.13)

Відображення щодо інших площин можна одержати шляхом комбінації обертання і відображення.

Просторовий перенос

Тривимірний лінійний перенос зображення задається виразом

(4.14)

Після перемножування одержимо

(4.15)

Тривимірне обертання навколо довільної осі

тривимірне обертання фігура відображення

Метод двовимірного плоского обертання навколо довільної осі був розглянений раніше. Узагальненням цього методу є спосіб обертання навколо довільної осі в тривимірному просторі. Як і для плоского випадку, розглянена процедура полягає в переносі зображення і заданої осі обертання, що забезпечує обертання навколо осі, що проходить через початок координат. Метод тривимірного обертання полягає в лінійному переносі, обертанні навколо початку координат і зворотньому лінійному переносі у вихідне положення. Якщо вісь, навколо якої виконується обертання, проходить через точку А = , то матриця перетворення визначається наступним виразом:

(4.16)

де елементи матриці обертання R розміру 4х4 визначаються в загальному випадку співвідношенням

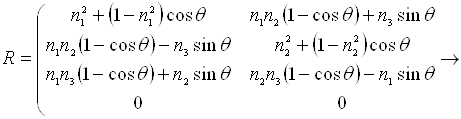
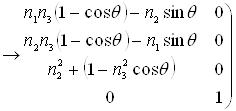(4.17)