Симплексний метод лінійного програмування
Завдання 1
Кондитерська фабрика для виробництва трьох видів карамелі А1, А2, А3 використовує три види сировини: цукор-пісок, патоку і фруктове пюре. Норми використання сировини кожного виду на виробництво однієї тони карамелі подано в таблиці, відома також загальна кількість сировини кожного виду і прибуток від реалізації 1 тонни карамелі певного виду.
| Вид сировини | Норми витрат сировини (т) на 1 т карамелі | Об’єм сировини, т | ||
А1 | А2 | А3 | ||
| Цукор-пісок | 0,8 | 0,5 | 0,6 | 1000 |
| Патока | 0,4 | 0,4 | 0,3 | 800 |
| Фруктове пюре | - | 0,1 | 0,1 | 150 |
| Прибуток від реалізації 1 т продукції (грн. од.) | 21 | 23 | 25 | |
Розв’язок
Складаємо математичну модель задачі. Позначимо через х1 кількість карамелі 1-го виду, що виготовляє підприємство за деяким планом, а через х2 кількість карамелі 2-го виду та через х3 кількість карамелі 3-го виду. Тоді прибуток, отриманий підприємством від реалізації цих виробів, складає
∫ = 21х1+23х2+25х3.
Витрати сировини на виготовлення такої кількості виробів складають відповідно:
CI =0,8х1+0,5х2+0,6х3,
CIІ =0,4х1+0,4х2+0,3х3,
CIІІ =0х1+0,1х2+0,1х3.
Оскільки запаси сировини обмежені, то повинні виконуватись нерівності:
0,8х1+0,5х2+0,6х3≤1000
0,4х1+0,4х2+0,3х3≤800
0х1+0,1х2+0,1х3≤150.
Оскільки, кількість виробів є величина невід'ємна, то додатково повинні виконуватись ще нерівності: х1> 0, х2> 0, х3>0.
Таким чином, приходимо до математичної моделі:
Знайти х1, х2, х3 такі, що функція ∫ = 21х1+23х2+25х3 досягає максимуму при системі обмежень:
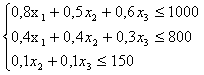
Розв'язуємо задачу лінійного програмування симплексним методом.
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
0,8x1 + 0,5x2 + 0,6x3 + 1x4 + 0x5 + 0x6 = 1000
0,4x1 + 0,4x2 + 0,3x3 + 0x4 + 1x5 + 0x6 = 800
0x1 + 0,1x2 + 0,1x3 + 0x4 + 0x5 + 1x6 = 150
де х1,...,х6>0
Матриця коефіцієнтів A = a(ij) цієї системи рівнянь має вигляд:
![]()
Базисні змінні це змінні, які входять лише в одне рівняння системи обмежень і притому з одиничним коефіцієнтом.
Вирішимо систему рівнянь відносно базисних змінних:
x4 , x5 , x6
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
X1 = (0,0,0,1000,800,150)
Оскільки завдання вирішується на максимум, то ведучий стовпець вибираємо по максимальному негативному кількістю та індексного рядку. Всі перетворення проводимо до тих пір, поки не вийдуть в індексному рядку позитивні елементи.
Складаємо симплекс-таблицю:
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 1 | x4 | 1000 | 0.8 | 0.5 | 0.6 | 1 | 0 | 0 | 1666.67 |
x5 | 800 | 0.4 | 0.4 | 0.3 | 0 | 1 | 0 | 2666.67 | |
x6 | 150 | 0 | 0.1 | 0.1 | 0 | 0 | 1 | 1500 | |
| Індексний рядок | F(X1) | 0 | -21 | -23 | -25 | 0 | 0 | 0 | 0 |
Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х3, оскільки значення коефіцієнта за модулем найбільше.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 2 | x4 | 100 | 0.8 | -0.1 | 0 | 1 | 0 | -6 | 125 |
x5 | 350 | 0.4 | 0.1 | 0 | 0 | 1 | -3 | 875 | |
x3 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 0 | |
| Індексний рядок | F(X2) | 37500 | -21 | 2 | 0 | 0 | 0 | 250 | 0 |
Даний план, також не оптимальний, тому будуємо знову нову симплексну таблицю. У якості ведучого виберемо елемент у стовбці х1.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 3 | x1 | 125 | 1 | -0.13 | 0 | 1.25 | 0 | -7.5 | 0 |
x5 | 300 | 0 | 0.15 | 0 | -0.5 | 1 | 0 | 2000 | |
x3 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 1500 | |
| Індексний рядок | F(X3) | 40125 | 0 | -0.63 | 0 | 26.25 | 0 | 92.5 | 0 |
Оскільки, в індексному рядку знаходяться негативні коефіцієнти, поточний опорний план неоптимальний, тому будуємо новий план. У якості ведучого виберемо елемент у стовбці х2, оскільки значення коефіцієнта за модулем найбільше.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | min |
| 4 | x1 | 312.5 | 1 | 0 | 0.13 | 1.25 | 0 | -6.25 | 0 |
x5 | 75 | 0 | 0 | -0.15 | -0.5 | 1 | -1.5 | 2000 | |
x2 | 1500 | 0 | 1 | 1 | 0 | 0 | 10 | 1500 | |
| Індексний рядок | F(X4) | 41062.5 | 0 | 0 | 0.63 | 26.25 | 0 | 98.75 | 0 |
Оскільки всі оцінки >0, то знайдено оптимальний план, що забезпечує максимальний прибуток: х1=312.5, х2=1500. Прибуток, при випуску продукції за цим планом, становить 41062,5 грн.
Завдання 2
Записати двоїсту задачу до поставленої задачі лінійного програмування. Розв’язати одну із задач симплексним методом і визначити оптимальний план іншої задачі. Оптимальні результати перевірити графічно.
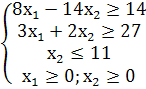
![]()
Розв’язок
Розв’яжемо задачу лінійного програмування симплексним методом.
Визначимо мінімальне значення цільової функції F(X)=5x1+3x2 при наступних умовах-обмежень.
8x1-14x2≥14
3x1+2x2≥27
x2≤11
Для побудови першого опорного плану систему нерівностей приведемо до системи рівнянь шляхом введення додаткових змінних.
8x1-14x2-1x3 + 0x4 + 0x5 = 14
3x1 + 2x2 + 0x3-1x4 + 0x5 = 27
0x1 + 1x2 + 0x3 + 0x4 + 1x5 = 11
Введемо штучні змінні x.
8x1-14x2-1x3 + 0x4 + 0x5 + 1x6 + 0x7 = 14
3x1 + 2x2 + 0x3-1x4 + 0x5 + 0x6 + 1x7 = 27
0x1 + 1x2 + 0x3 + 0x4 + 1x5 + 0x6 + 0x7 = 11
Для постановки задачі на мінімум цільову функцію запишемо так:
F(X) = 5x1+3x2+Mx6+Mx7 => min
Вважаючи, що вільні змінні рівні 0, отримаємо перший опорний план:
X1 = (0,0,0,0,11,14,27)
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | х6 | х7 |
| 0 | х6 | 14 | 8 | -14 | -1 | 0 | 0 | 1 | 0 |
x7 | 27 | 3 | 2 | 0 | -1 | 0 | 0 | 1 | |
х5 | 11 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | |
| Індексний рядок | F(X0) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Переходимо до основного алгоритму симплекс-методу.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | х7 | min |
| 1 | х6 | 14 | 8 | -14 | -1 | 0 | 0 | 1 | 0 | 1.75 |
x7 | 27 | 3 | 2 | 0 | -1 | 0 | 0 | 1 | 9 |
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

