Скачать

Симметрия - символ красоты, гармонии и совершенства

Когда мы проходили по геометрии тему «Симметрия», то на нее было отведено очень мало времени, а мне показалось эта тема интересной, и я решила взять ее для исследования. Мне захотелось побольше узнать по данному вопросу, ведь я уже ни раз слышала данный термин на других предметах и в быту. Приступив к исследованию, я заметила, что симметрия не только математическое понятие, она проявляется как нечто прекрасное в живой и неживой природе, а также в творениях человека. Поэтому я поставила перед собой такие проблемные вопросы:

l Как проявляется гармоничность симметрии в природе;

l Какие виды симметрий, встречаются в природе;

l Как применяет красоту симметрии в своих творениях человек?

Поэтому тему своего исследования я назвала «Симметрия — символ красоты, гармонии и совершенства».

§2. Что такое симметрия? Ее виды в геометрии.

О, симметрия! Гимн тебе пою!

Тебя повсюду в мире узнаю.

Ты в Эйфелевой башне, в малой мошке,

Ты в елочке, что у лесной дорожки.

С тобою в дружбе и тюльпан, и роза,

И снежный рой – творение мороза!

А что же такое симметрия? В толковом словаре С.И. Ожегова симметрия истолковывается, как «соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости». Из этого же словаря я узнала, что слово гармония означает «согласованность, стройность в сочетании чего-нибудь». Мы видим, что симметрия и гармония связаны между собой.

В начале я рассмотрю какие виды симметрии встречаются в школьном курсе геометрии, а это:

l центральная (относительно точки)

l осевая ( относительно прямой)

l зеркальная (относительно плоскости).

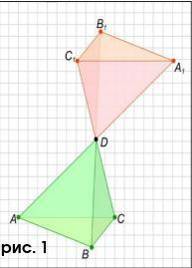
Центральная симметрия.

Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией (см.рис. 1).

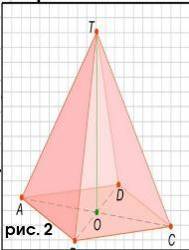
Осевая симметрия.

Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямой а, также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией (см. рис. 2).

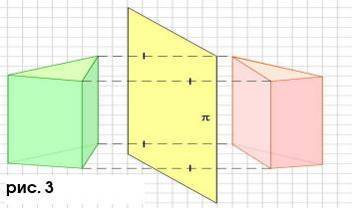
Зеркальная симметрия.

Зеркальной симметрией (симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно этой плоскости точку М1(см. Рис 3).

Теперь я хочу, понаблюдав и изучив специальную литературу, посмотреть, где найдет свое отображение симметрия. Почему мы находим одни вещи красивыми, а другие нет? Почему смотреть на симметричные изображения приятнее, нежели на асимметричные?

§3. Проявление симметрии в живой и неживой природе

Красота в природе не создаётся, а лишь фиксируется, выражается. Рассмотрим проявление симметрии с «глобального», а именно с нашей планеты Земля.

То, что Земля — шар, стало известно образованным людям еще в древности. Земля в представлении большинства начитанных людей до эпохи Коперника была центром мироздания. Поэтому прямые, проходящие через центр Земли, они считали центром симметрии Вселенной. Поэтому даже макет Земли – глобус имеет ось симметрии (см. рис. 4).

· Далее я рассмотрела проявление симметрии в живой природе. Почти все живые существа построены по законам симметрии, недаром в переводе с греческого слово «симметрия» означает «соразмерность».

Среди цветов, например, наблюдается поворотная симметрия. Многие цветы можно повернуть так, что каждый лепесток займет положение соседнего, цветок совместится с самим собой. Минимальный угол такого поворота для различных цветов неодинаков. Для ириса он равен 120° (см. рис. 5), для колокольчика – 72° (см. рис. 6), для нарцисса – 60° (см. рис. 7). В расположении листьев на стеблях растений наблюдается винтовая симметрия. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света (см. рис. 8), хотя сами листья тоже имеют ось симметрии (см. рис. 9). Рассматривая общий план строения какого-либо животного, мы замечаем обычно известную правильность в расположении частей тела или органов, которые повторяются вокруг некоторой оси или занимают одно и то же положение по отношению к некоторой плоскости. Эту правильность называют симметрией тела. Явления симметрии столь широко распространены в животном мире, что весьма трудно указать группу, в которой никакой симметрии тела подметить нельзя. Симметрией обладают и маленькие насекомые, и крупные животные (см.рис. 10,11, 12).

· Среди бесконечного разнообразия форм неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. Наблюдая за красотой природы, можно заметить, что при отражении предметов в лужах, озерах проявляется зеркальная симметрия.

Видите? Это же голая зеркальность!

Глупая, глупая природа, ни о чем она не заботится так рьяно,

как о равновесии (см. рис. 13).

(Венедикт Ерофеев)

В мир неживой природы очарование симметрии вносят кристаллы (см.рис.14). Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают поворотной симметрией и, кроме того, зеркальной симметрией (см. рис. 15).

А что такое кристалл? Твердое тело, имеющее естественную форму многогранника. Соль, лед, песок и т.д. состоят из кристаллов. Прежде всего Ромэ-Делиль подчёркивал правильную геометрическую форму кристаллов исходя из закона постоянства углов между их гранями. Он писал: «К разряду кристаллов стали относить все тела минерального царства, для которых находили фигуру геометрического многогранника…» Правильная форма кристаллов возникает по двум причинам. Во-первых, кристаллы состоят из элементарных частичек - молекул, которые сами имеют правильную форму. Во-вторых, «такие молекулы имеют замечательное свойство соединяться между собой в симметричном порядке».

Почему же так красивы и привлекательны кристаллы? Их физические и химические свойства определяются их геометрическим строением. В кристаллографии (науке о кристаллах) существует даже раздел, который называется «Геометрическая кристаллография». В 1867 году генерал от артиллерии, профессор Михайловской академии в Петербурге А.В. Гадолин строго математически вывел все сочетания элементов симметрии, характеризующие кристаллические многогранники. Например, гранат попадает в первую, так называемую кубическую систему, все кристаллы которой имеют те же элементы симметрии, что и куб

(форму куба имеют, например, кристаллы поваренной соли). Всего существует 32 вида симметрий идеальных форм кристалла.

Легко вообразить, какая бы царила на Земле неразбериха, если бы симметрия в природе была нарушена!

§4. Применение законов симметрии человеком

Увидев проявление симметрии в природе, мне захотелось узнать, применяет ли человек эти закономерности в своих творениях.

Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле — как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство». Г. Вейль под симметрией понимал «неизменность какого-либо объекта, при определенного, рода преобразованиях; предмет является симметричным, в том случае, когда его можно подвергнуть какой-нибудь операции, после которой он будет выглядеть так же, как и до преобразования». Определенную главу Г. Вейль посвятил орнаментной симметрии. Упорядоченность и подчиненность определенному набору правил мы обнаруживаем в узорах и орнаментах (см. рис. 16).

Нельзя не увидеть симметрию и в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Так как гранат имеет те же элементы что и куб, он высоко ценится знатоками драгоценных камней. Художественные изделия из гранатов были обнаружены в могилах Древнего Египта, относящихся еще к додинастическому периоду (свыше двух тысячелетий до н.э.).

В коллекциях Эрмитажа особым вниманием пользуются золотые украшения древних скифов. Необычайно тонка художественная работа золотых венков, диадем, дерева и украшенных драгоценными красно-фиолетовыми гранатами (см.рис. 17, 18).

Одним из самых наглядных использований законов симметрии в жизни служат строения архитектуры. Это то, что чаще всего мы можем увидеть. В архитектуре оси симметрии используются как средства выражения архитектурного замысла. Примеров использования симметрии в архитектуре множество, одним из них является прекрасный Новосибирский театр оперы и балета (см. рис. 19). И даже у нас, в г. Купино есть здание, имеющее симметрию – здание Администрации Купинского района (см. рис. 20).

Еще одним примером использования человеком симметрии в своей практике - это техника. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Или одно из важнейших изобретений человечества, имеющих центр симметрии, является колесо (см. рис. 21), также центр симметрии есть у пропеллера и других технических средств.

Симметрию можно заметить даже там, на что никогда не обращал внимание. Например, если вы поместите буквы перед зеркалом, расположив его параллельно строке, то заметите, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».

Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф означает именно истинную середину.

Симметрия также есть и в числах, например, √12345678987654321=111111111; √123454321=11111 и т.д.

симметрия центральная осевая зеркальная геометрия

Заключение

Изучив и исследовав тему «Симметрии» я узнала, что помимо осевой, зеркальной и центральной видов симметрии, которые мы изучаем в школьном курсе, существуют и другие виды симметрии, например в природе – поворотная, винтовая, в кристаллографии вообще - 32 вида.

Таким образом, изучая симметрию законов природы, рано или поздно удается глубже проникнуть в сущность живого, объяснить ход эволюции и дать возможность человеку чаще применять данные законы симметрии в жизни.

Рассматривая архитектуру зданий, предметы украшения и быта, технические изобретения, мы видим в них присутствие центральной, поворотной, переносной, осевой и зеркальной видов симметрии, которые дают ощущение спокойной уверенности и эстетической привлекательности.

Симметрия, проявляясь в самых различных объектах природного мира, несомненно, отражает наиболее общие ее свойства. Поэтому изучение симметрии разнообразных природных объектах и сопоставление его (изучения) результатов удобным и надежным инструментом познания гармонии мира.

Литература

1) Тарасов Л.В. Этот удивительно симметричный мир. – М.: Просвещение, 1982.

2)  Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» //Математика в школе. – 1996. - № 3. – С. 60.

3) Кошелев А.И. Проявление симметрии в различных формах материи.

4) Вейль Г. Симметрия. М.: Едиториал УРСС, 2003

5) Климова Н.Т. Народный орнамент в композиции художественных изделий. - М.: Изобразительное искусство, 1993.

6) О. Иванова. Этот симметричный мир. - Первое сентября. – 2006 № 6.

Приложения

Симметрия и ее виды в геометрии.