Решение транспортных задач
Математика необходима в повседневной жизни, следовательно определенные математические навыки нужны каждому человеку. Нам приходится в жизни считать(например, деньги), мы постоянно используем(часто не замечая этого) знания о величинах, характеризующих протяженности, площади, объемы, промежутки времени, скорости и многое другое. Все это пришло к нам на уроках арифметики и геометрии и пригодилось для ориентации в окружающем мире.
Математические знания и навыки нужны практически во всех профессиях, прежде всего, конечно, в тех, что связаны с естественными науками, техникой и экономикой. Математика является языком естествознания и техники и потому профессия естествоиспытателя и инженера требует серьезного овладения многими профессиональными сведениями, основанными на математике.
Хорошо сказал об этом Галилей:
«Философия (на нашем языке- физика) написана в величайшей книге, которая постоянно открыта вашему взору, но понять ее может лишь тот, кто сначала научится понимать ее язык и толковать знаки, которыми она написана. Написана же она на языке математики».
Сегодня несомненна необходимость применения математических знаний и математического мышления врачу, лингвисту, историку, и людям других специальностей. Но особенно знание математики необходимы людям точных профессий - финансистам, экономистам.
Профессиональный уровень экономиста во многом зависит от того, освоил ли он современный математический аппарат и умеет ли использовать его при анализе сложных экономических процессов и принятий решений. Поэтому в подготовке экономистов широкого профиля изучения математики занимает значительное место. Математическая подготовка экономиста имеет свои особенности, связанные со спецификой экономических задач, а также с широким разнообразием подходов к их решению.
Задачи практической и теоретической экономики очень разносторонни. К ним относятся, в первую очередь, методы сбора и обработки статической информации, а также оценка состояния и перспективы развития экономических процессов. Применяются различные способы использования полученной информации - от простого логического анализа до составления сложных экономико-математических моделей и разработки математического аппарата их исследования.
Неопределенность экономических процессов, значительный случайный разброс и большой объем получаемой информации обуславливают необходимость привлечения к исследованию экономических задач теории вероятностей и математической статистики.
Наряду с моделированием экономистам необходимо изучать теорию оптимизации, которая представлена математическими методами исследования операций, в том числе линейным программированием.
Отмеченные направления требуют знания основополагающего математического аппарата: основ линейной алгебры и математического анализа, теории вероятностей и математического программирования.
Таким образом, математика и математическое образование нужны для подготовки к будущей профессии.
Один из классов математических моделей- задачи линейного программирования. Одной из задач линейного программирования является транспортная задача- задача составления оптимального плана перевозок, позволяющего минимизировать суммарный километраж. Транспортная задача, как и задача линейного программирования была впервые поставлена советским экономистом А.Н.Толстым в 1930 году. Разработка общих методов решения задачи линейного программирования и их математическое исследование связано с именем советского ученого Л.В.Канторовича. В 1939 году методам решения задачи линейного программирования посвящено также большое число работ зарубежных ученых. Основной метод решения задачи линейного программирования –симплекс метод- был опубликован в 1949 году Дандигом. Симплекс метод дает решение любой задачи линейного программирования, но если переменных очень много, то решение весьма затруднительно и для более сложных задач симплекс метод стали модифицировать.
Транспортная задача делится на два вида: транспортная задача по критерию стоимости- определение плана перевозок, при котором стоимость груза была бы минимальна; транспортная задача по критерию времени- более важным является выигрыш по времени.
Транспортная задача по критерию стоимости является частным случаем задачи линейного программирования и может быть решена симплексным методом. Однако в силу особенностей задачи, она решается намного проще.
1. ОСНОВНАЯ ЧАСТЬ
1.1 МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Транспортная задача-
Однородный груз сосредоточен у т поставщиков в объемах ![]() .
.
Данный груз необходимо доставить п потребителям в объемах ![]() .
.
Известны ![]() (i=1,2,…,m; j=1,2,…,n)- стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.
(i=1,2,…,m; j=1,2,…,n)- стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.
Исходные данные транспортной задачи записываются в таблице вида
Таблица 1
|
| … |
| |
|
|
| … |
|
|
|
| … |
|
… | … | … | … | … |
|
|
| … |
|
Переменными(неизвестными) транспортной задачи являются ![]() (i=1,…,m;i=1,2,…,n)- объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в матрице перевозок
(i=1,…,m;i=1,2,…,n)- объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в матрице перевозок 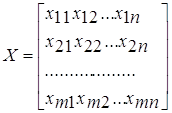
Математическая модель транспортной задачи в общем случае имеет вид
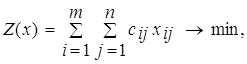 (1.1)
(1.1)
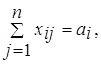 i=1,2,…,m, (1.2)
i=1,2,…,m, (1.2)
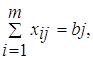 j=1,2,…,n, (1.3)
j=1,2,…,n, (1.3)
![]() i=1,2,…,m; j=1,2,…,n. (1.4)
i=1,2,…,m; j=1,2,…,n. (1.4)
Целевая функция задачи (1.1) выражает требования обеспечить минимум суммарных затрат на перевозку всех грузов. Первая группа из т уравнений (1.2) описывает тот факт, что запасы всех т поставщиков вывозятся полностью. Вторая группа из n уравнений (1.3) выражает требования полностью удовлетворить запросы всех n потребителей. Неравенства (1.4) являются условиями неотрицательности всех переменных задачи.
Таким образом, математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи
![]() i=1,2,…,m; j=1,2,…,n,
i=1,2,…,m; j=1,2,…,n,
удовлетворяющее системе ограничений (1.2), (1.3), условиям неотрицательности (1.4) и обеспечивающее минимум целевой функции (1.1).
В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е.
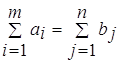 .
.
Такая задача называется задачей с правильным балансом, а ее модель- закрытой. Если же это неравенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель- открытой.
Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей, т.е. задача должна быть с правильным балансом.
Пример 1:
Составить математическую модель транспортной задачи перевоза груза из двух складов в 3 магазина:
Таблица 2
| 50 | 70 | 80 |
| 90 | 9 | 5 | 3 |
| 110 | 4 | 6 | 8 |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Решения задач линейного программирования геометрическим методом
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ«ПРИДНЕСТРОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. Т.Г. ШЕВЧЕНКО»РЫБНИЦКИЙ ФИЛИАЛКАФЕДРА «Ф
- Решения задачи планирования производства симплекс методом
- Рівняння регресії і побудова економетричних моделей
- Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича
ОБЛАСНИЙ КОМУНАЛЬНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД "ІНСТИТУТ ПІДПРИЄМНИЦТВА "СТРАТЕГІЯ"КАФЕДРА ЕКОНОМІЧНОЇ КІБЕРНЕТИКИКурсова роботаЗ дисц
- Розв'язок задач лінійного програмування. Задача планування виробництва
- Розвиток економетричних моделей та методів в розвинутих країнах та приклади їх застосування в Україні
ЗмістВступ1. Економетрія та прогнозування2. Прикладні економетрічні моделі Франції та США3. Макроеконометричні моделі УкраїниВисновокС
- Розв’язування економетричних задач
Лабораторна робота № 1Тема. Застосування електронних таблиць EXCEL та пакетів прикладних програм для розв’язування економетричних задач
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

