Решения задачи планирования производства симплекс методом
1. Обзор научно-технической литературы
1.1 История развития экономико-математического планирования
1.2 Необходимость решения задач линейного программирования
1.3 Линейное программирование
1.4 Математическая формулировка задачи линейного программирования
1.5 Постановка задачи целочисленного программирования
2. Обзор основных алгоритмов решения задач ЛП
2.1 Целочисленное линейное программирование - метод отсечений Гомори
2.1.1 Отсечения
2.1.2 Описание алгоритма
2.2 Целочисленное линейное программирование - метод ветвей и границ
2.2.1 Общее описание
2.2.2 Применение
2.2.3 Алгоритм решения
2.3 Симплекс метод
2.3.1 Описание
2.3.2 Алгоритм симплекс-метода
2.3.2.1 Усиленная постановка задачи
2.3.2.2 Алгоритм
2.4 Решение задач оптимизации при помощи средства «Поиск решения» в Microsoft Excel
2.4.1 Описание
2.4.2 Процедура поиска решения
2.4.3 Параметры средства «Поиск решения»
3. Задача планирования производства
3.1 Постановка задачи планирования производства в общем случае
3.2 Математическое описание поставленной задачи планирования симплекс методом
3.3 Решение поставленной задачи планирования производства
3.3.4 Проверка признака допустимости и оптимальности базиса
3.3.5 Нахождение разрешающего элемента в симплекс-таблице. Формирование нового базиса
3.3.6 Пересчет симплекс-таблицы
3.4 Результат решения задачи планирования производства
4. Программа для решения задач ЛП симплекс методом
4.1 Описание
4.2 Графическое представление программы
4.3 Работа с программой
4.4 Схема программы
Заключение
Список литературы
В процессе хозяйственной деятельности сырьевая база предприятия занимает одно из центральных мест, поэтому вопрос об оптимизации сырья на предприятии при планировании выпускаемой продукции актуален в настоящее время.
Актуальность данной темы также заключается в том, что в процессе производственной деятельности все предприятия сталкиваются с проблемой нехватки сырья, а также с тем, что выпускаемая продукция должна быть адекватна с экономической точки зрения, другими словами, чтобы её можно было выгодно продать, и чтобы она соответствовала запросам покупателя.
Учитывая всевозрастающую ограниченность ресурсов, очень важно добиваться их максимально эффективного использования. План должен быть разработан настолько умело, чтобы использование ограниченных ресурсов было оптимальным.
Существует много причин, заставляющих промышленные предприятия заниматься оптимизацией структуры сырья:
улучшение финансовых показателей;
повышение уровня производства;
наращивание объемов производства.
Планирование выпуска продукции также имеет огромное значение для предприятия, оно тесно взаимосвязано с сырьевой базой предприятия.
Сущность планирования продукции состоит в обосновании целей и способов их достижения на основе выявления комплекса задач и работ, а также определения эффективных методов и способов, ресурсов всех видов, необходимых для выполнения этих задач и установления их взаимодействия.
Оптимизация структуры сырья при планировании выпуска продукции является существенным источником резервов увеличения суммы прибыли. Логично предположить, что предприятию выгодно увеличивать доли тех изделий, которые приносят максимальную прибыль. Но всегда следует помнить о ряде ограничений, не позволяющих отказаться от менее рентабельной продукции:
1) Потенциальный спрос на продукцию достаточно динамичен и дифференцирован во времени и пространстве. Те изделия и торговые марки, которые востребованы в данный момент времени, могут потерять свою потребительскую привлекательность через некоторые промежутки времени;
2) Основные производственные фонды нуждаются в постоянной эксплуатации, наладке и обслуживании. Простои оборудования – это всегда неблагоприятный фактор для производства.
Планом выпуска продукции определяются:
Количественные показатели производства;
Объем реализации, ожидаемый в планируемом периоде. Этот показатель определяется на основе объема выпуска продукции и ожидаемой средней цены реализации 1 учетной единицы продукции. Ожидаемая средняя цена реализации определяется на основе ретроспективного анализа данных за предыдущие несколько лет с учетом ожидаемых и текущих темпов инфляции.
Для каждого периода, охватываемого планом, необходимо определить две переменные: объём производства в данный период; количество ресурсов, используемых в данный период.
План выпуска продукции отражает номенклатуру и ассортимент производства продукции в соответствии с планом реализации, обязательствами предприятия и экономическими условиями.
Планирование выпускаемой продукции включает решение ряда задач. Прежде всего, планируется номенклатура, ассортимент и объем выпуска продукции. Номенклатура производства представляет собой перечень изделий (готовых изделий, полуфабрикатов и т. п.), подлежащих изготовлению на предприятии в плановом периоде. Ассортимент продукции характеризует соотношение удельных весов отдельных видов изделий в общем, выпуске продукции. Номенклатура, ассортимент и объем изготовляемой предприятием продукции устанавливаются на основе централизованного задания по поставкам важнейших видов продукции и портфеля заказов предприятия с учетом его специализации. При этом учитываются и договоры по кооперированным поставкам, заключенные предприятием.
Целесообразно совершенствовать структуру выпуска только той продукции, удельный вес которой в общем объеме выпуска достаточно высок.
Необходимым условием увеличения количества производства определенных изделий является универсальность оборудования для их производства.
План выпуска продукции может повлиять на величину целого ряда издержек, в том числе: издержки хранения готовой продукции; издержки ведения портфеля отложенных заказав; издержки, связанные с внеурочной работой или простоем работников; издержки, связанные с передачей части работ субподрядчикам; издержки, связанные с наймом и увольнением работников.
Задача оптимизации структуры сырья при планировании выпуска продукции должна решаться на каждом промышленном предприятии, которое заинтересовано в максимизации прибыли от продажи выпускаемой продукции. Такая задача является задачей линейного программирования.
Данная дипломная работа состоит из теоретической и практической частей. В теоретической части рассматривается алгоритм решения оптимизационной задачи линейного программирования. В практической части рассматривается задача планирования производства выпускающего несколько видов продукции из ограниченного количества ресурсов для достижения максимальной прибыли. Так же реализуется программный интерфейс в среде объектно-ориентированного программирования С++, для решения поставленной задачи симплекс методом.
1. Обзор научно-технической литературы
1.1 История развития экономико-математического планирования
В 1938-1939 гг. ленинградский математик (впоследствии академик, лауреат Ленинской, Государственных и Нобелевской премий) Л.В. Канторович в результате анализа ряда проблем организации и планирования производства сформулировал новый класс условно-экстремальных задач и предложил методы их решения. Так было положено начало новой отрасли прикладной математики линейному программированию. В более поздних работах Л. В. Канторович расширил область применения линейного программирования в социалистической экономике, сформулировав задачи отраслевого и народнохозяйственного оптимального планирования. А через два десятилетия после своего возникновения линейное программирование стало основным инструментом плановоэкономических решений на всех уровнях социалистического народного хозяйства.
В том же 1939 г. ленинградский экономист В. В. Новожилов, рассматривая эффективность плановых и проектных решений, сформулировал важные теоретические положения, ставшие потом органической частью теории оптимального планирования социалистической экономики.
Далее методы планирования продолжали совершенствоваться, но только развитие вычислительной техники в конце 50-х гг. позволило сделать плановые многовариантные расчеты достаточно распространенными. Важную роль в организации и пропаганде экономико-математических исследований в этот период сыграл академик В. С. Немчинов. Именно в эти годы получают развитие некоторые разделы прикладной математики, связанные с решением оптимизационных задач: линейное и нелинейное программирование, теория оптимального управления и др. В 60-е гг. основное внимание исследователей сосредоточивается на разработке оптимизационных моделей различных типов и их практическом применении к решению задач планирования. Было построено большое количество экономико-математических моделей, на основе которых проведены расчеты по составлению реальных оптимальных планов (оптимальные планы перевозок, эксплуатации подвижного состава транспорта, использования топлива, загрузки оборудования предприятий; оптимальное размещение отдельных отраслей промышленности и предприятий отрасли; оптимальное планирование и распределение капиталовложений и т. д.), что дало большой народнохозяйственный эффект. Наряду с расширением сферы применения математических моделей в экономике и планировании осуществляется процесс усовершенствования моделей и использования более адекватного математического аппарата: переход от статических моделей к динамическим, от жестко детерминированных к стохастическим моделям, учитывающим случайность и неопределенность экономических процессов, применение дискретного программирования, методов статистического моделирования, создание новых алгоритмов, позволяющих решать задачи большой размерности.
1.2 Необходимость решения задач линейного программирования
Применение экономико-математических методов и моделей позволяет существенно улучшить качество планирования и получить дополнительный экономический эффект без вовлечения в общественное производство дополнительных ресурсов, что чрезвычайно важно в условиях перехода экономики на преимущественно интенсивный путь развития.
В настоящее время область возможного применения экономико-математических методов в планировании чрезвычайно велика и с каждым годом она расширяется. Однако область фактического их применения в практике плановых расчетов намного скромнее. Это объясняется трудностями широкого внедрения экономико-математических методов.
К числу их следует отнести: сложность определения критерия оптимальности в ряде экономических задач; трудности при решении проблемы «встраивания» математических моделей в существующую систему планирования и управления, приводящие к необходимости создания новой технологии планирования, базирующегося на системном использовании экономико-математических методов и ЭВМ; стохастический и динамический характер экономических процессов, требующий усложнения используемого математического аппарата и программного обеспечения ЭВМ, увеличения объема вычислений; трудность измерений многих экономических явлений и получения массовой достоверной информации для наполнения разработанных моделей; трудность проверки правильности (верификации) экономикоматематических моделей, ориентированных не столько на подтверждение действительности, сколько на решение новых социально-экономических задач (это в первую очередь относится к моделям планирования и прогнозирования), и т. д.
Но главная трудность заключается в сложности моделируемых экономических процессов и явлений. Большинство объектов, изучаемых экономической наукой, может быть охарактеризовано кибернетическим понятием «сложная система». При изучении систем недостаточно (а иногда и невозможно) пользоваться методом расчленения на элементы с последующим изучением этих элементов в отдельности.
Кроме того, моделирование существенно усложняется тем, что экономика охватывает не только производственные процессы, но и производственные отношения. Моделировать производственные отношения невозможно, не учитывая поведение людей, их интересы и индивидуально принятые решения.
В результате производственно-хозяйственная или социально-экономическая ситуация, в которой приходится принимать плановые решения, часто оказывается намного богаче и сложнее тех моделей, которые используются в планировании в этой ситуации.
В настоящее время линейное программирование является одним из наиболее употребительных аппаратов математической теории оптимального принятия решений, в том числе и в финансовой математике. Для решения задач линейного программирования разработано сложное программное обеспечение, дающее возможность эффективно и надежно решать практические задачи больших объемов. Эти программы и системы снабжены развитыми системами подготовки исходных данных, средствами их анализа и представления полученных результатов. В развитие и совершенствование этих систем вложен труд и талант многих математиков, аккумулирован опыт решения тысяч задач. Владение аппаратом линейного программирования необходимо каждому специалисту в области прикладной математики.
Линейное программирование представляет собой наиболее часто используемый метод оптимизации. К числу задач линейного программирования можно отнести задачи:
рационального использования сырья и материалов; задачи оптимального раскроя;
оптимизации производственной программы предприятий;
оптимального размещения и концентрации производства;
составления оптимального плана перевозок, работы транспорта;
управления производственными запасами;
и многие другие, принадлежащие сфере оптимального планирования.
Для большого количества практически интересных задач целевая функция выражается линейно – через характеристики плана, причем допустимые значения параметров подчинены линейным равенствам или неравенствам. Нахождение при данных условиях абсолютного экстремума целевой функции носит название линейного программирования.
Первым исследованием по линейному программированию является работа Л. В. Канторовича “Математические методы организации и планирования производства”, опубликованная в 1939 г. В нем дана постановка задач линейного программирования, разработан метод разрешающих множителей решения задач линейного программирования и дано его теоретическое обоснование.
Прямая задача линейного программирования является математической формулировкой проблемы составления такого плана использования различных способов производства, который позволяет получить максимальное количество однородного продукта при имеющихся в наличии ресурсах.
Математическое программирование – это прикладная отрасль математики, которая является теоретической основой решения задач оптимального планирования.
Существуют следующие разделы математического программирования: линейное, параметрическое, нелинейное и динамическое программирование. Наиболее разработанным и широко применяемым разделом математического программирования является линейное программирование, целью которого служит отыскивание оптимума (max, min) заданной линейной функции при наличии ограничений в виде линейных уравнений или неравенств.
Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.
Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.
Термин «программирование» нужно понимать в смысле «планирования». Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, еще до того, как компьютеры были использованы для решения линейных задач оптимизации.
1.4 Математическая формулировка задачи линейного программирования
Нужно определить максимум линейной целевой функции (линейной формы)
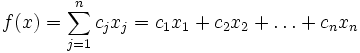
при условиях
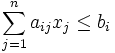 при
при ![]() .
.
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют "основной" или "стандартной" в линейном программировании.
1.5 Постановка задачи целочисленного программирования
По смыслу значительной части экономических задач, относятся к задачам линейного программирования, компоненты решения должны выражаться в целых числах, т.е. быть целочисленными. К ним относятся, например, задачи, в которых переменные означают количество единиц неделимой продукции, число станков при загрузке оборудования, число судов при распределениях по линиям, число турбин в энергосистеме, число вычислительных машин в управляющем комплексе и многие другие.
Задача линейного целочисленного программирования формируется следующим образом: найти такое решение (план) X = (x1,x2,...,xn), при котором линейная функция
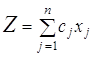 (1)
(1)
принимает максимальное или минимальное значение при ограничениях
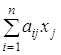 =bi, i=1, 2…,m. (2)
=bi, i=1, 2…,m. (2)
хj ³ 0, j=1, 2,...,n.(3)
xj — целые числа (4)
2. Обзор основных алгоритмов решения задач ЛП
2.1 Целочисленное линейное программирование - метод отсечений Гомори
Целочисленное линейное программирование (сокращенно ЦЛП) занимается задачами линейного программирования с целочисленными переменными, общая задача формулируется следующим образом: найти max{сх|Ах ≤ b; х - целочисленный}. ЦЛП может рассматриваться так же, как поиск точки решетки, принадлежащей многограннику или как решение системы линейных уравнений с целыми неотрицательными переменными. Иными словами, в ЦЛП рассматриваются совместные ограничения неотрицательность и целочисленность.
С помощью отсечений выделяют целочисленные части полиэдров. Метод отсечений был разработан в конце 1950-х годов Гомори для решения целочисленных линейных программ с помощью симплекс-метода. Метод отсечений оказался полезным и с теоретической точки зрения он дает возможность описать целочисленную оболочку полиэдра.
Далее описывается метод отсечений Гомори, дающий алгоритм решения задач целочисленного линейного программирования. Данный метод, который также носит название метода отсекающих плоскостей, предназначен для решения ЦЗЛП (целочисленной задачи линейного программирования) в канонической форме.
Описываемая ниже версия алгоритма предназначена для решения полностью целочисленных задач, т.е. таких, у которых все параметры aij, cj, bi – целые.
Приведем обобщенную схему алгоритма Гомори. Структурно он делится на так называемые большие итерации. Каждая большая итерация содержит этапы:
1.Сначала задача решается методами линейного программирования (малые итерации), обычно симплекс-методом, и анализируется результат, если результатом являются целые числа, то на этом решение заканчивается, а если дробные, то производят следующие операции:
2. В оптимальном плане (симплекс-таблице) выбирают строку, в которой целая часть дробного(!) свободного члена (P0) принимает наибольшее значение.
3.Построение для найденной компоненты условия отсечения.
Исходя из уравнения по данной строке xr=P0r - ar,1*x1 - … - ar,n*xn в систему ограничений добавляем неравенство, в котором коэффициенты будут дробными частями коэффициентов данного уравнения:
{P0r} –{ar,1}*x1 - … -{ar,n}*xn ≤ 0.
Переводим к каноническому виду добавляя новую переменную xn+1, получим:
{P0r} –{ ar,1}*x1 - … - {ar,n}*xn+xn+1= 0
И соответственно добавляем в симплекс-таблицу новый базисный вектор по новой переменной xn+1.
4.Переход на начало следующей большой итерации.
Замечание:
При добавлении в симплекс-таблицу нового базисного вектора по новой переменной xn+1 мы получаем недопустимое (отрицательное) решение. Для того, чтобы избавиться от недопустимого решения выбираем столбец замещения так, чтобы строкой замещения стала новая добавленная строка по переменной xn+1. Продолжаем пересчет симплекс-таблицы. Если снова получаем дробное решение, то еще вводим дополнительный базисный вектор, и так до получения целочисленного решения. Но следует заметить, что если область допустимых решений очень мала, то она может и не содержать целых значений, это необходимо проверить графически. Если область допустимых решений не содержит целочисленного решения, то в применении метода Гомори нет необходимости, целого решения не будет!
2.2 Целочисленное линейное программирование - метод ветвей и границ
Метод ветвей и границ — общий алгоритмический метод для нахождения оптимальных решений различных задач оптимизации, особенно дискретной и комбинаторной оптимизации. По существу, метод является комбинаторным (алгоритм перебора) с отсевом подмножеств множества допустимых решений, не содержащих оптимальных решений. Его суть заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.
Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.
Метод был впервые предложен Ленд и Дойг в 1960 г. для решения задач целочисленного линейного программирования.
Общая идея метода может быть описана на примере поиска минимума и максимума функции f(x) на множестве допустимых значений x. Функция f и x могут быть произвольной природы. Для метода ветвей и границ необходимы две процедуры: ветвление и нахождение оценок (границ).
Процедура ветвления состоит в разбиении области допустимых решений на подобласти меньших размеров. Процедуру можно рекурсивно применять к подобластям. Полученные подобласти образуют дерево, называемое деревом поиска или деревом ветвей и границ. Узлами этого дерева являются построенные подобласти.
Процедура нахождения оценок заключается в поиске верхних и нижних границ для оптимального значения на подобласти допустимых решений.
В основе метода ветвей и границ лежит следующая идея (для задачи минимизации): если нижняя граница для подобласти A дерева поиска больше, чем верхняя граница какой-либо ранее просмотренной подобласти B, то A может быть исключена из дальнейшего рассмотрения (правило отсева). Обычно, минимальную из полученных верхних оценок записывают в глобальную переменную m; любой узел дерева поиска, нижняя граница которого больше значения m, может быть исключен из дальнейшего рассмотрения.
Если нижняя граница для узла дерева совпадает с верхней границей, то это значение является минимумом функции и достигается на соответствующей подобласти.
Метод используется для решения некоторых NP-трудных задач, такие как:
Задача коммивояжера
Задача о ранце
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Пусть им является план X0. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи и Fmax = F(Xo).
Если же среди компонент плана X0 имеются дробные числа, то X0 не удовлетворяет условию целочисленности и необходимо осуществить упорядоченный переход к новым планам, пока не будет найдено решение задачи. Покажем, как это можно сделать, предварительно отметив, что F(X0) ³ F(X) для всякого последующего плана X.
Предполагая, что найденный оптимальный план X0 не удовлетворяет условию целочисленности переменных, тем самым считаем, что среди его компонент есть дробные числа. Пусть, например, переменная ![]() приняла в плане X0 дробное значение. Тогда в оптимальном целочисленном плане ее значение будет по крайней мере либо меньше или равно ближайшему меньшему целому числу
приняла в плане X0 дробное значение. Тогда в оптимальном целочисленном плане ее значение будет по крайней мере либо меньше или равно ближайшему меньшему целому числу ![]() , либо больше или равно ближайшему большему целому числу
, либо больше или равно ближайшему большему целому числу ![]() +1. Определяя эти числа, находим симплексным методом решение двух задач линейного программирования:
+1. Определяя эти числа, находим симплексным методом решение двух задач линейного программирования:
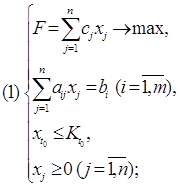
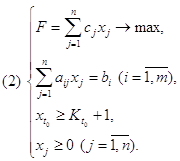
Найдем решение задач линейного программирования (I) и (II). Очевидно, здесь возможен один из следующих четырех случаев:
1. Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции на нем и дают решение исходной задачи.
2. Одна из задач неразрешима, а другая имеет оптимальный план, среди компонент которого есть дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу, и строим две задачи, аналогичные задачам (I) и (II).
3. Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на этих планах и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и он вместе со значением целевой функции на нем дает искомое решение.
Если же значение целевой функции больше на плане, среди компонент которого есть дробные числа, то следует взять одно из таких чисел и для задачи, план которой рассматривается, необходимо построить две задачи, аналогичные (I) и (II).
4. Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем значение целевой функции на данных оптимальных планах и рассматриваем ту из задач, для которой значение целевой функции является наибольшим. В оптимальном плане этой задачи выбираем одну из компонент, значение которой является дробным числом, и строим две задачи, аналогичные (I) и (II).
Таким образом, описанный выше итерационный процесс может быть представлен в виде некоторого дерева, на котором исходная вершина отвечает оптимальному плану Х0 задачи (1)-(3), а каждая соединенная с ней ветвью вершина отвечает оптимальным планам задач (I) и (II). Каждая из этих вершин имеет свои ветвления. При этом на каждом шаге выбирается та вершина, для которой значение функции является наибольшим. Если на некотором шаге будет получен план, имеющий целочисленные компоненты, и значение функции на нем окажется больше или равно, чем значение функции в других возможных для ветвления вершинах, то данный план является оптимальным планом исходной задачи целочисленного программирования и значение целевой функции на нем является максимальным.
Итак, процесс нахождения решения задачи целочисленного программирования (1)-(4) методом ветвей и границ включает следующие основные этапы:
1). Находят решение задачи линейного программирования (1)-(3).
2). Составляют дополнительные ограничения для одной из переменных, значение которой в оптимальном плане задачи (1)-(3) является дробным числом.
3). Находят решение задач (I) и (II), которые получаются из задачи (1)-(3) в результате присоединения дополнительных ограничений.
4). В случае необходимости составляют дополнительные ограничения для переменной, значение которой является дробным, формулируют задачи, аналогичные задачам (I) и (II), и находят их решение.
Итерационный процесс продолжают до тех пор, пока не будет найдена вершина, соответствующая целочисленному плану задачи (1)-(3) и такая, что значение функции в этой вершине больше или равно значению функции в других возможных для ветвления вершинах.
Описанный выше метод ветвей и границ имеет более простую логическую схему расчетов, чем метод Гомори.
В узлах метода ветвей и границ используется симплекс-метод.
Главный недостаток алгоритма метода ветвей и границ заключается в необходимости полностью решать задачи линейного программирования, ассоциированные с каждой из вершин многогранника допустимых решений. Для задач большой размерности это требует значительных и, в известной степени, неоправданных с практической точки зрения затрат времени.
Задачи линейного программирования в канонической форме широко распространены в инженерной практике, и для их решения разработана большая группа методов, основной из которых — симплекс-метод. Рассмотрим постановку и решение задачи линейного программирования в канонической форме.
Задача будет рассматриваться в форме, которая называется канонической. Известно, что путем введения дополнительных ограничений и переменных можно свести к канонической форме задачу линейного программирования, представленную в любой форме, в частности в естественной форме.
2.3.2 Алгоритм симплекс-метода
2.3.2.1 Усиленная постановка задачи
Задачи линейного программирования имеет следующий вид:
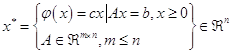
с помощью конечно-сходящейся вычислительной процедуры симплекс-метода, заданной оператором
![]()
В операторе векторы ![]() и
и ![]() — оптимальное решение задачи и начальное приближение для симплекс-метода, которые в симплекс-методе являются базисными решениями, определяемыми ниже. Векторы
— оптимальное решение задачи и начальное приближение для симплекс-метода, которые в симплекс-методе являются базисными решениями, определяемыми ниже. Векторы ![]() и
и ![]() представляют собой последующее и предыдущее решения в симплекс-методе.
представляют собой последующее и предыдущее решения в симплекс-методе.
Алгоритм симплекс-метода формулируется для задачи линейного программирования следующим образом:
Шаг 1. Формулировка задачи линейного программирования в канонической форме на основе метода искусственного базиса, так чтобы в матрице ограничений существовала единичная базисная матрица. Для этого необходимо дополнить матрицу ограничений единичными столбцами, которые должны в совокупности с исходными столбцами матрицы ограничений обеспечивать существование единичной базисной матрицы. При этом естественным образом должны быть введены соответствующие искусственные переменные, которые включаются в целевую функцию с большими положительными весовыми коэффициентами для задачи на минимум. В результате запишем исходную матрицу ограничений ![]() . в симплекс-таблицу(*), а коэффициенты целевой функции
. в симплекс-таблицу(*), а коэффициенты целевой функции ![]() запишем в строку этой таблицы. В таблицу(*) также включим компоненты исходного базисного решения, определяемого вектором
запишем в строку этой таблицы. В таблицу(*) также включим компоненты исходного базисного решения, определяемого вектором ![]()
Таблица (*)
| #№ | Базисные столбцы | Bs | Базисное решение Xs | C1 | C2 | … | Cm | Cm+1 | … | Ck | … | Cn |
| A1 | A2 | … | Am | Am+1 | … | Ak | … | An | ||||
| 1 | A1 |
|
| 1 | 0 | … | 0 |
| … |
| … |
|
| 2 | A2 |
|
| 0 | 1 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| l | Al |
|
| 0 | 0 | … | 0 |
| … |
| … |
|
| … | … | … | … | … | … | … | … | … | … | … | … | … |
| m | Am |
|
| 0 | 0 | … | 1 |
| … |
| … |
|
| Оценки |
|
| … |
|
| … |
| … |
|
Шаг 2. Вычисление характеристических разностей (оценок) по формулам и запись оценок в ![]() -ю строку симплекс-таблицы.
-ю строку симплекс-таблицы.
Шаг 3. Вычисление оценки ![]() , удовлетворяющей условию:
, удовлетворяющей условию:
Если все ![]() , то в соответствии с выполнением критерия оптимальности вектор
, то в соответствии с выполнением критерия оптимальности вектор ![]() — оптимальное решение, и далее следует перейти к шагу 9, иначе — к шагу 4.
— оптимальное решение, и далее следует перейти к шагу 9, иначе — к шагу 4.
Шаг 4. Вычисление нового базисного решения ![]() из условия:
из условия:
![]()
Шаг 5. Вычисление компонент нового базисного решения ![]() по формулам:
по формулам:
![]()
Шаг 6. Вычисление элементов новой симплекс-таблицы для ![]() -й итерации метода по формулам:
-й итерации метода по формулам:
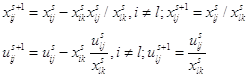
Шаг 7. Корректировка симплекс-таблицы с учетом изменений коэффициентов целевой функции, соответствующих новому базисному решению. Формируем таблицу (**).
Таблица (**)
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

