Рівняння регресії і побудова економетричних моделей
ЗМІСТ
Завдання 1. Побудова економетричної моделі парної регресії 2
Завдання 2. Побудова економетричної моделі множинної регресії 2
Розв’язання завдання 1. 3
Розв’язання завдання 2. 8
3. Регресійний аналіз. 8
Завдання 1. Побудова економетричної моделі парної регресії
На основі даних про витрати обігу (залежна змінна) і вантажообігу (незалежна змінна) побудувати економетричну модель:
· оцінити параметри моделі за методом найменших квадратів;
· визначити коефіцієнти кореляції та детермінації;
· оцінити значимість регресійної моделі за критерієм Фішера;
· оцінити значимість параметрів моделі регресії;
· виконати точкове прогнозування yn+1 для ![]() , де р = 0,95;
, де р = 0,95;
· обчислити інтервали довіри для залежної змінної при α = 0,05;
· зробити висновок.
Таблиця 1. Вихідні дані для розрахунку (варіант 9)
| Х (незалежна змінна) | У (залежна змінна) |
| 0,15 | 1,35 |
| 0,34 | 1,39 |
| 0,09 | 1,27 |
| 0,05 | 1,10 |
| 0,48 | 1,23 |
| 0,41 | 1,39 |
| 0,62 | 1,38 |
| 0,50 | 1,35 |
| 1,2 | 1,24 |
| 0,21 | 1,40 |
Завдання 2. Побудова економетричної моделі множинної регресії
На основі даних таблиці (таблиця 2) спостережень побудувати найкраще рівняння регресії:
· побудувати кореляційну матрицю, використовуючи процедуру Кореляція;
· визначити наявність мультиколінеарності;
· провести регресійний аналіз, використовуючи процедуру Регресія;
· побудувати рівняння регресії і оцінити статистичні характеристики;
· визначити найкраще рівняння регресії.
Таблиця 2
Вихідні дані для розрахунку (варіант 9)
| У | Х1 | Х2 | Х3 |
| 9,4 | 0,23 | 1,35 | 173,9 |
| 9,9 | 0,43 | 1,39 | 162,3 |
| 9,1 | 0,26 | 1,27 | 101,2 |
| 5,5 | 0,43 | 1,10 | 177,8 |
| 6,6 | 0,38 | 1,23 | 93,2 |
| 4,3 | 0,42 | 1,39 | 126,7 |
| 7,4 | 0,30 | 1,38 | 91,8 |
| 6,6 | 0,37 | 1,35 | 70,6 |
| 5,5 | 0,34 | 1,24 | 97,2 |
| 9,4 | 0,23 | 1,40 | 80,3 |
Розв’язання завдання 1.
Рівняння регресії має наступний вигляд: ŷ![]() . Розрахуємо необхідні для оцінки методом найменших квадратів коефіцієнти b0 і b1. Проміжні розрахунки наведено в Додатку 1.
. Розрахуємо необхідні для оцінки методом найменших квадратів коефіцієнти b0 і b1. Проміжні розрахунки наведено в Додатку 1.
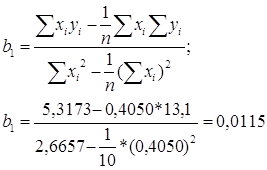
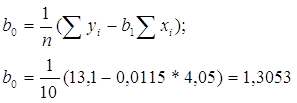
Отже, відповідно до методу найменших квадратів, рівняння регресії має вигляд: ŷ ![]()
Визначимо коефіцієнти кореляції та детермінації.
Коефіцієнт парної детермінації
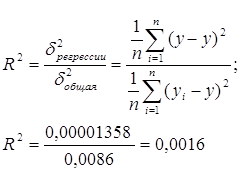
Висновок: коефіцієнт парної детермінації R2 складає 0,0016. Це означає, що тільки 0,16% змін змінної у визначається лінійною залежністю від змінної х. Такий зв’язок дуже малий для подальшого аналізу і не здатний надати точних результатів для подальшого прогнозування.
Для перевірки коефіцієнту детермінації висуваємо гіпотези:
Н0: R2 = 0 (лінійної залежності немає).
Н1: R2 ≠ 0 (лінійна залежність є).
Обираємо рівень значущості α – за умовами він дорівнює 0,05.
α = 0,05.
Визначаємо ступінь свободи k:
k1 = m = 1
k2 = n – 2 = 10 – 2 = 8
n – кількість спостережень; m – кількість пояснювальних змінних.
Скориставшись таблицею Фішера, визначимо, що F0,05 = 5,32.
Определим F-статистику:
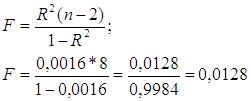
F < F0,05. Отже, гіпотезу R2 ≠ 0 відкидаємо з п’ятивідсотковим ризиком помилитись і приймаємо гіпотезу Н0: R2 = 0. Таким чином, з імовірністю більше 95% можна стверджувати, що між змінними х та у не існує лінійної залежності.
Коефіцієнт кореляції rxy:
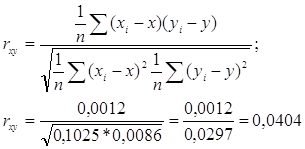
Повинна виконуватись умова ![]() .
.
У нашому випадку (0,0404) 2 ≈ 0,0016 ≈ R2. Приблизна рівність означає, що розрахунки проведено вірно.
Висновок: коефіцієнт кореляції rxy складає 0,0404. Це означає, що між змінними х та у існує дуже слабка лінійна залежність.
Для перевірки надійності коефіцієнту кореляції визначимо t-статистику:
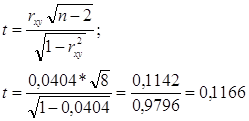
Повинна виконуватись умова ![]() .
.
В нашому випадку (0,1166) 2 ≈ 0,0136 ≈ F. Приблизна рівність (F = 0,0128) означає, що в розрахунках були погрішності, але через їхню незначущість ними можна зневажати.
3. Оцінка значущості параметрів моделі. Побудування інтервалів довіри.
I. Оцінімо параметр b0. Для цього розрахуємо коефіцієнт статистику t0.
b0 = 1,3053
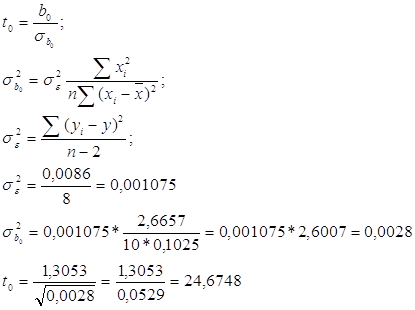
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
Рівень значущості α = 0,05
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
![]()
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за95% оцінка b0 є статистично значущою, що потребує розрахунку інтервалу довіри.
β0 = b0 ± t0,05*σb0 = 1,3053 ± 2,31*0,0529 = 1,3053 ± 0,122199
Р(1,183101< β0 < 1,427499) = (1 – α) *100% = 95%
Таким чином, в генеральній сукупності β0 з імовірністю 95% знаходиться в інтервалі (1,183101; 1,427499).
II. Оцінімо параметр b1.
b1 = 0,0115
Визначимо t-статистику для b1:
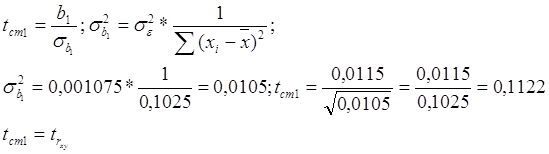
В нашому випадку tст1 ≈ trxy. Приблизна рівність допустима (trxy = 0,1166) і означає, що в розрахунках були погрішності, якими можна зневажати.
Висуваємо гіпотези:
H0: β0 = 0
H1: β0 ≠ 0
tст1 = 0,1122
Рівень значущості α = 0,05.
Кількість ступенів свободи k = n – 2; k = 10 – 2 = 8.
За допомогою таблиці теста Стьюдента визначимо, що t0,05 = 2,31.
tст1< t0,05.
Висновок: за п’ятивідсоткового рівня значущості можна стверджувати, що з імовірністю, більшою за 95%, оцінка параметра b1 не є статистично значущою, звідки робимо висновок, що інтервал довіри не розраховується.
4. Точкове прогнозування yn+1 для ![]() , де р = 0,95.
, де р = 0,95.
ŷn+1 = b0 + b1*xn+1
ŷn+1 = 1,3053 + 0,0115*11 = 1,4318.
Висновок: отже, за прогнозними даними в 11-му періоді значення залежної змінної дорівнюватиме 1,4318. Але, як було вказано раніше, ці прогнозні значення навряд чи можна вважати достовірними, тому що коефіцієнти детермінації та кореляції відповідають дуже слабкому рівню зв’язку між змінними.
Розв’язання завдання 2
1. Кореляційна матриця.
За допомогою Пакету аналізу Excel побудуємо кореляційну матрицю, використовуючи операцію Кореляція (рис.1).
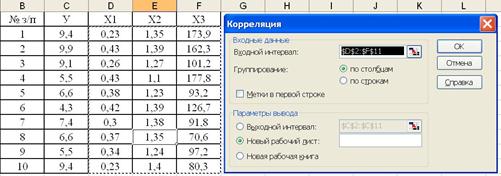
Рис.1. Процес побудови кореляційної матриці.
Таблиця 1. Кореляційна матриця Excel
| Стовпчик 1 | Стовпчик 2 | Стовпчик 3 | |
| Стовпчик 1 | 1 | ||
| Стовпчик 2 | -0,30202801 | 1 | |
| Стовпчик 3 | 0,279578475 | -0,25820294 | 1 |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Рішення систем нелінійних рівнянь. Метод ітерацій. Метод Ньютона–Канторовича
ОБЛАСНИЙ КОМУНАЛЬНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД "ІНСТИТУТ ПІДПРИЄМНИЦТВА "СТРАТЕГІЯ"КАФЕДРА ЕКОНОМІЧНОЇ КІБЕРНЕТИКИКурсова роботаЗ дисц
- Розв'язок задач лінійного програмування. Задача планування виробництва
Розв'язок задач лінійного програмування. Задача планування виробництваМета роботи:Набути навичок складання математичної моделі задач
- Розвиток економетричних моделей та методів в розвинутих країнах та приклади їх застосування в Україні
ЗмістВступ1. Економетрія та прогнозування2. Прикладні економетрічні моделі Франції та США3. Макроеконометричні моделі УкраїниВисновокС
- Розв’язування економетричних задач
Лабораторна робота № 1Тема. Застосування електронних таблиць EXCEL та пакетів прикладних програм для розв’язування економетричних задач
- Структура графа состояний клеточных автоматов определённого типа
Управление образования Московского района г. МинскаГосударственное учреждение образования СШ № 41 г. МинскаСтруктура графа состояний к
- Структура системного анализа
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮГосударственное образовательное учреждение высшего профессионального образованияРОССИЙСКИЙ ГО
- Структура эконометрики
РЕФЕРАТСтруктура современной эконометрикиСтруктура современной эконометрикиЭконометрика – это наука, изучающая конкретные количест
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

