referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Обусловленность матрицы
Министерство образования и науки российской федерации
Федеральное агентство по образованию
Новосибирский государственный технический университет
Бердский филиал
Расчетно-графическая работа
по курсу: «Вычислительная математика»
Выполнила:
Студентка II курса
Булгакова Н.
Группы ВТБ-81
Проверил:
Преподаватель
Голубева Елена Николаевна
г. 362964Бердск,
2010
Задание 1 Обусловленность матрицы
Задание: Дана система уравнений ax=b порядка n. Исследовать зависимость погрешности решения x от погрешностей правой части системы b.
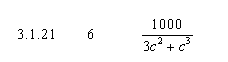
погрешность уравнение координата интерполяция дифференциальный
1. Задать матрицу системы A и вектор правой части b, найти решение x системы Ax=b с помощью метода Гаусса.
2. Принимая решение x, полученное в п.1, за точное, вычислить вектор 
относительных погрешностей решений 
систем 
,где компоненты векторов 
вычисляются по формулам:
(
-произвольная величина погрешности).
3. На основе вычисленного вектора d построить гистограмму. По гистограмме определить компоненту 
, вектора b, которая оказывает наибольшее влияние на погрешность решения.
4. Вычислить число обусловленности cond(A) матрицы A.
5. Оценить теоретически погрешность решения 
по формуле:
Сравнить значение 
со значением практической погрешности 
Объяснить полученные результаты.
Решение
1. Задаём матрицу А.
Для заполнения используем код программы zapolnenie.cpp (см. приложение)
#include
#include
#include
#include
#include
#include
main()
{
double matr(100)(100);
for (int i=1;i<7;i++)
{
for (int j=1;j<7;j++)
matr(i)(j)= 1000/(3*(pow(0.1*21*i*j,2))+pow(0.1*21*i*j,3));
}
for ( int j=1;j<7;j++)
{
for ( int i=1;i<7;i++)
printf("%10.4f",matr(j)(i));
printf("\n");
}
getchar();
}
Результат работы zapolnenie:
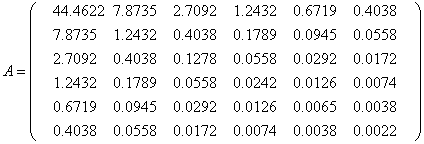
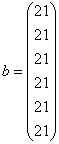
Найдем решение полученной матрицы используя программу gauss.cpp (см приложение)
Исходный код gauss.cpp:
#include
#include
#include
#include
#include
#include
const int sz=6;
double A(sz)(sz)={
{44.4622, 7.8735, 2.7092, 1.2432, 0.6719, 0.4038},
{7.8735, 1.2432, 0.4038, 0.1789, 0.0945, 0.0558},
{2.7092, 0.4038, 0.1278, 0.0558, 0.0292, 0.0172},
{1.2432, 0.1789, 0.0558, 0.0242, 0.0126, 0.0074},
{0.6719, 0.0945, 0.0292, 0.0126, 0.0065, 0.0038},
{0.4038, 0.0558, 0.0172, 0.0074, 0.0038, 0.0022}
} ;
double F(sz)={21.00,21.00,21.00,21.00,21.00,21.00} ;
double X(sz);
double b(sz+1),par;
// функция вывода матрицы на экран
void Viv(double A(sz)(sz))
{
int i,j;
for( i=0;i { for( j=0;j printf(" %.4f ",A(i)(j)); //вывод на экрам исходной матрицы с заданным количеством знаков после запятой (5f) printf(" %.4f ",F(i)); cout< } system("pause"); } /////////////// функция решения методом Гаусса void Resh(double A(sz)(sz),double F(sz),double X(sz)) { int i,j,k; for (k=0;k { // проверяем первый элемент if (A(k)(k)==0) //проверка на неноль { for (i=k;A(i)(k)==0;i++); // находим ненулевой 1й элемент for(j=k;j { par=A(k)(j); //смена строк в матрице A(k)(j)=A(i)(j); //путем записи в par и извлечения из него A(i)(j)=par; } par=F(k); // смена строк в ответе F(k)=F(i); F(i)=par; } // получаем 1й элемент единицу (делим всю первую строку на a1,1 ) par=A(k)(k); //пишем в par первый элемент for(int i=k;i A(k)(i)=A(k)(i)/par; F(k)=F(k)/par; // делим ответ на 1й // нулевой столбец for(int j=k+1;j { for(int i=k;i b(i)=A(k)(i)*A(j)(k); b(sz)= F(k)*A(j)(k); for(int i=k;i A(j)(i)-=b(i); F(j)-=b(sz); } } for(i=sz-1;i>=0;i--) //обратка { par=0; for (j=0;j par+=A(i)(sz-j-1)*X(sz-1-j); X(i)=F(i)-par; } } //функция - точка входа в программу void main() { Viv(A); // выводим матрицу Resh(A,F,X); // решаем матрицу A методом Гаусса for(int i=0;i system("pause"); } Результат работы gauss: ==================================================== точное ==================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 872.15582 X(1)= -16329.24792 X(2)= 10011.59140 X(3)= 111650.80126 X(4)= -26697.87796 X(5)= -144076.29603 Для продолжения нажмите любую клавишу . . . ====================================================== 2. Вычисляем вектор d. Величина погрешности, вносимой в правую часть системы – 1%. Сформируем векторы b (по заданному закону) Для каждого из них найдем решение матрицы, используя gauss С погрешностью в …. компоненте ====================================================== в первой ====================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 20.7900 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 872.07580 X(1)= -16327.25169 X(2)= 10005.24500 X(3)= 111652.84781 X(4)= -26679.82743 X(5)= -144100.68447 Для продолжения нажмите любую клавишу . . . ====================================================== во второй ====================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 20.7900 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 874.15205 X(1)= -16398.19981 X(2)= 10378.69292 X(3)= 111250.49388 X(4)= -27254.14851 X(5)= -143256.57148 Для продолжения нажмите любую клавишу . . . ====================================================== в третьей ====================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 20.7900 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 865.80942 X(1)= -15962.14640 X(2)= 7652.50187 X(3)= 114149.98680 X(4)= -23271.06118 X(5)= -148104.07985 Для продолжения нажмите любую клавишу . . . ====================================================== в четвёртой ====================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 20.7900 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 874.20237 X(1)= -16729.55530 X(2)= 12510.77695 X(3)= 111600.37766 X(4)= -35532.05319 X(5)= -138409.12992 Для продолжения нажмите любую клавишу . . . ====================================================== в пятой ====================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 20.7900 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 21.0000 Для продолжения нажмите любую клавишу . . . X(0)= 890.20635 X(1)= -16885.51847 X(2)= 13438.40819 X(3)= 102816.62603 X(4)= -16375.93145 X(5)= -148185.68530 Для продолжения нажмите любую клавишу . . . ====================================================== в шестой ===================================================== 44.4622 7.8735 2.7092 1.2432 0.6719 0.4038 21.0000 7.8735 1.2432 0.4038 0.1789 0.0945 0.0558 21.0000 2.7092 0.4038 0.1278 0.0558 0.0292 0.0172 21.0000 1.2432 0.1789 0.0558 0.0242 0.0126 0.0074 21.0000 0.6719 0.0945 0.0292 0.0126 0.0065 0.0038 21.0000 0.4038 0.0558 0.0172 0.0074 0.0038 0.0022 20.7900 Для продолжения нажмите любую клавишу . . . X(0)= 847.76738 X(1)= -15509.52337 X(2)= 5983.80758 X(3)= 117317.96737 X(4)= -30807.26724 X(5)= -140960.86219 Для продолжения нажмите любую клавишу . . .b1 b2 b3 b4 b5 b6 20,79 21 21 21 21 21 21 20,79 21 21 21 21 21 21 20,79 21 21 21 21 21 21 20,79 21 21 21 21 21 21 20,79 21 21 21 21 21 21 20,79