Полином Жегалкина
Теоретическая часть
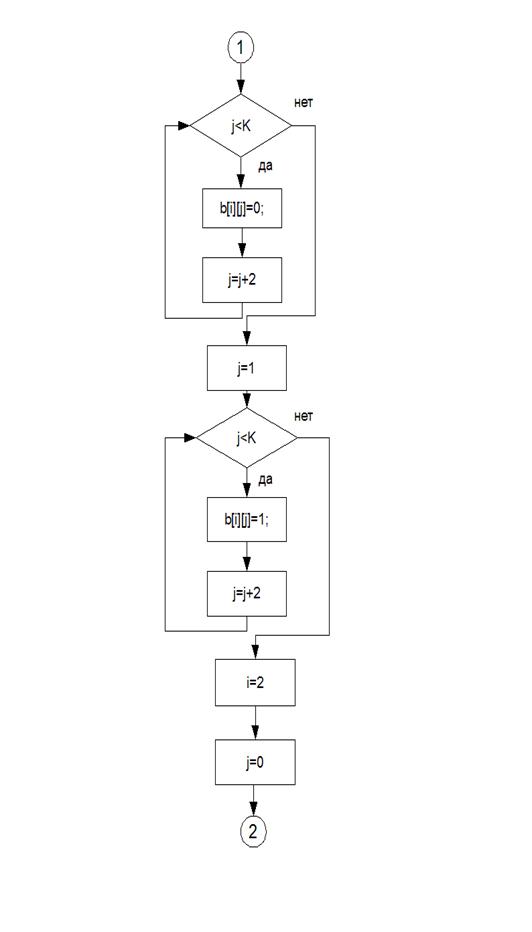
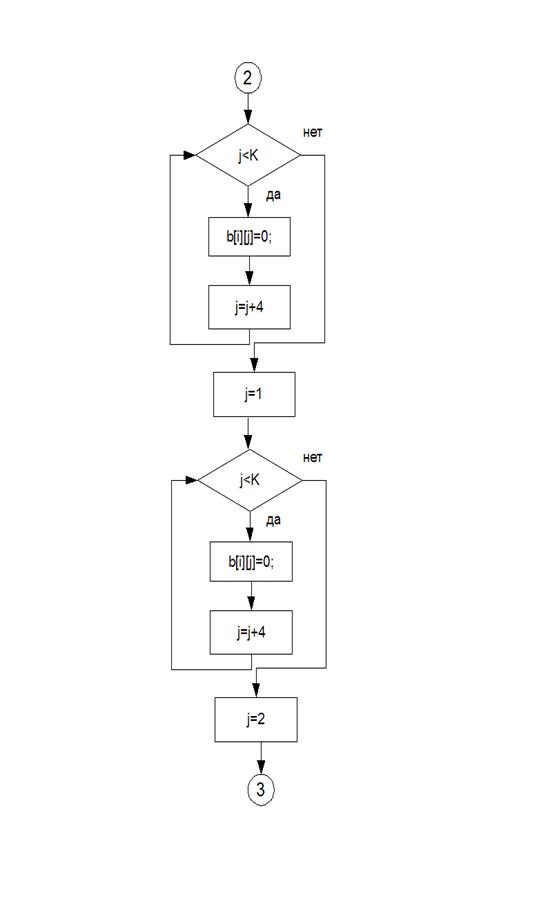
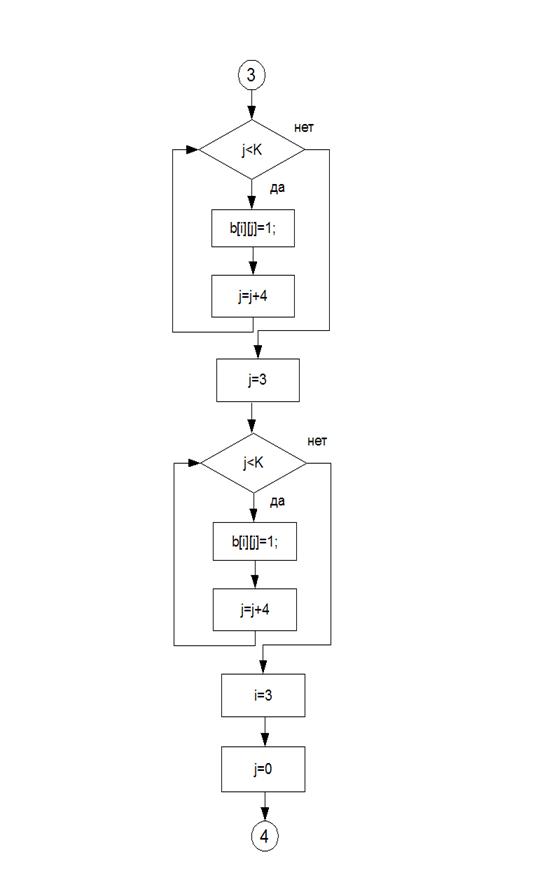
Алгоритм
Блок-схемы
Листинг программы
Тестирование программы
Заключение
Список использованной литературы:
Цель работы
Целью данной работы является изучение булевых функций, разработка алгоритма их представления в виде полинома Жегалкина и написания программы, реализующей этот алгоритм.
Введение
В курсе дискретной математики изучаются функции, область определения которых – дискретное множество. Простейшим (но нетривиальным) таким множеством является множество, состоящее из двух элементов.
Теоретическая часть
Полнота и замкнутость
Определение 1: Система функций ![]() из P2 (множества всех булевых функций) называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы.
из P2 (множества всех булевых функций) называется функционально полной, если любая булева функция может быть записана в виде формулы через функции этой системы.
Пример:
1) Само множество ![]() ;
;
2)![]() ;
;
3)![]() - не полна.
- не полна.
Теорема 1. Пусть даны две системы функций из ![]()
![]() , (I)
, (I)
![]() . (II)
. (II)
Известно, что система I полная и каждая функция системы I выражается через функции системы II. Тогда система II является полной.
Доказательство: Пусть ![]() . В силу полноты системы I , функцию h можно выразить в виде формулы
. В силу полноты системы I , функцию h можно выразить в виде формулы ![]() .
.
По условию теоремы
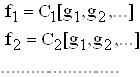
Поэтому
![]() ч. т. д.
ч. т. д.
Примеры:
1) ![]() - полная.
- полная.
2) ![]() - тоже полная, так как
- тоже полная, так как ![]() .
.
3) ![]() - тоже полная.
- тоже полная.
4) ![]() - тоже полная, так как
- тоже полная, так как
![]() ,
,
![]() ,
,
![]() . ((2) – I)
. ((2) – I)
5) ![]() - неполная.
- неполная.
Докажем это от противного.
Предположим, что ![]() .
.
Но ![]() .
.
Противоречие.
6) ![]() - неполная (сохраняет константу 0).
- неполная (сохраняет константу 0).
6’) ![]() - полная.
- полная.
7) ![]() - неполная (сохраняет константу 1).
- неполная (сохраняет константу 1).
8) ![]()
![]()
![]() тогда взяв в качестве системы I систему 2) можно заключить, система функций 8) – полная. Тем самым, справедлива
тогда взяв в качестве системы I систему 2) можно заключить, система функций 8) – полная. Тем самым, справедлива
Теорема Жегалкина. Каждая функция из ![]() может быть выражена при помощи полинома по модулю 2 – (полинома Жегалкина):
может быть выражена при помощи полинома по модулю 2 – (полинома Жегалкина):
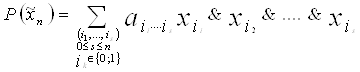 ,
,
где ![]() . (1)
. (1)
Имеем: число разных сочетаний ![]() равно числу подмножеств множества из n элементов. Каждое aik может принимать одно из 2-х значений {0,1}. Тогда число разных полиномов Жегалкина равно
равно числу подмножеств множества из n элементов. Каждое aik может принимать одно из 2-х значений {0,1}. Тогда число разных полиномов Жегалкина равно ![]() , т.е. равно числу различных булевых функций.
, т.е. равно числу различных булевых функций.
Т. о. получаем единственность представления функций через полином Жегалкина.
Способы представления функции в виде полинома Жегалкина
1) Алгебраические преобразования
![]() .
.
Пример:
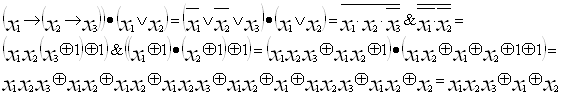
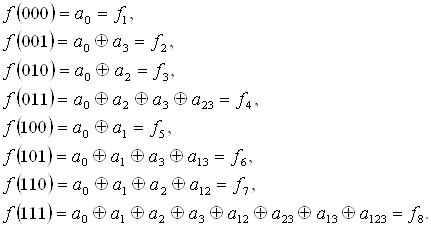
2) Метод неопределенных коэффициентов
![]() - искомый полином Жегалкина (реализующий функцию
- искомый полином Жегалкина (реализующий функцию ![]() ).
).
Вектор ![]() из формулы (1) будем называть вектором коэффициентов полинома
из формулы (1) будем называть вектором коэффициентов полинома ![]() .
.
Нам нужно найти неизвестные коэффициенты ![]() .
.
Поступаем так. Для каждого составим ![]() уравнение
уравнение ![]() , где
, где ![]() - выражение, получаемое из (1) при
- выражение, получаемое из (1) при ![]() . Это дает систему из
. Это дает систему из ![]() уравнений с
уравнений с ![]() неизвестными, она имеет единственное решение. Решив систему, находим коэффициенты полинома
неизвестными, она имеет единственное решение. Решив систему, находим коэффициенты полинома ![]() .
.
3) Метод, базирующийся на преобразовании вектора значения функции
Пусть ![]() - вектор значений функции.
- вектор значений функции.
Разбиваем вектор ![]() на двумерные наборы:
на двумерные наборы:
![]() .
.
Операция T определена следующим образом:
![]() .
.
Применяем операцию Т к двумерным наборам:

Используя построенные наборы, конструируем четырехмерные наборы, которые получаются в результате применения операции Т к четырехмерным наборам, выделяемым из ![]() .
.
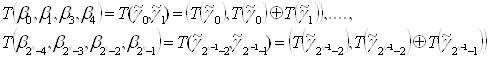
Затем от четырехмерных наборов переходим (аналогично) к восьмимерным и т.д., пока не построим ![]() - мерный набор. Он и будет искомым вектором коэффициентов полинома
- мерный набор. Он и будет искомым вектором коэффициентов полинома ![]() .
.
Пример:
Пусть вектор значений функций ![]() = (0,0,0,1,0,1,1,1)
= (0,0,0,1,0,1,1,1)

Полученный вектор является искомым векторов коэффициентов полинома ![]() .
.
Определение 2: Пусть M – некоторое подмножество функций из P2. Замыканием M называется множество всех булевых функций, представимых в виде формул через функции множества M. Обозначается (M).
Замечание. Замыкание инвариантно относительно операций введения и удаления фиктивных переменных.
Примеры.
1) M=P2, (M)=P2.
2) M={1,x1Åx2}, (M) – множество L всех линейных функций вида
![]() , (ciÎ{0,1}).
, (ciÎ{0,1}).
Свойства замыкания:
1) Если М замкнуто, то (M)=M;
2) ((M))=(M);
3) M1ÍM2 Þ (M1)Í(M2);
4) (M1ÈM2)Ê(M1)È(M1).
Определение 3. Класс (множество) M называется (функционально) замкнутым, если (M)=M.
Примеры.
1) Класс M=P2 функционально замкнут;
2) Класс {1,x1Åx2} не замкнут;
3) Класс L замкнут (линейное выражение, составленное из линейных выражений линейно).
Новое определение полноты. M – полная система, если (M)=P2.
булевой функция полином жигалкин
В данной программе был реализован метод неопределенных коэффициентов для построения полинома Жегалкина.
1. Получить таблицу истинности для определенного количества переменных;
2. Заполнить значения функции для каждого из наборов таблицы истинности;
3. Последовательно вычислить неизвестные коэффициенты;
4. Записать функцию в виде полинома Жегалкина с вычисленными коэффициентами.
| x1 | x2 | x3 | f |
| 0 | 0 | 0 | f1 |
| 0 | 0 | 1 | f2 |
| 0 | 1 | 0 | f3 |
| 0 | 1 | 1 | f4 |
| 1 | 0 | 0 | f5 |
| 1 | 0 | 1 | f6 |
| 1 | 1 | 0 | f7 |
| 1 | 1 | 1 | f8 |
![]() .
.
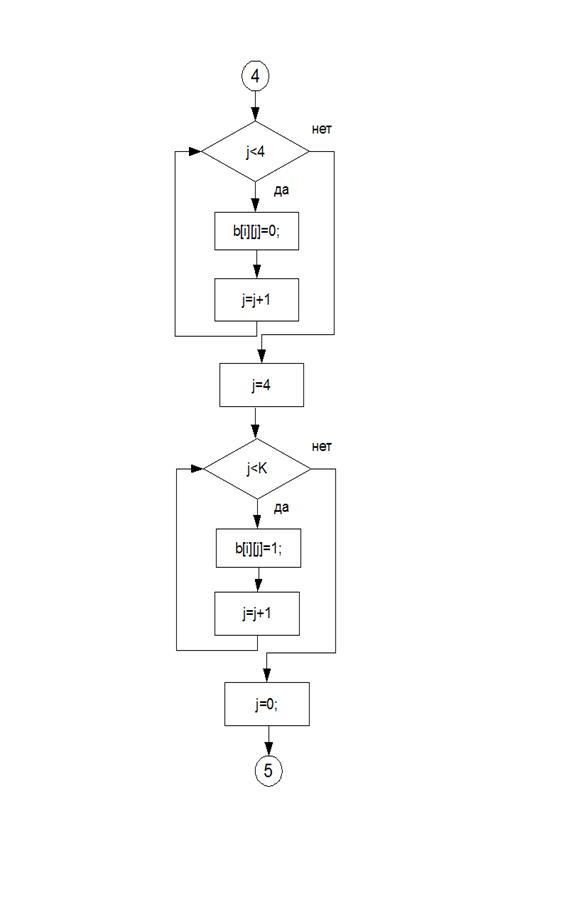
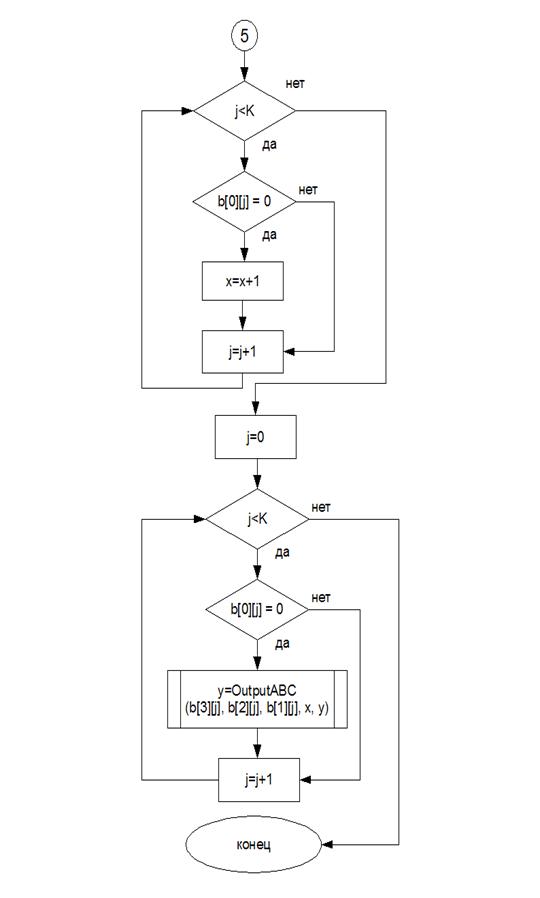
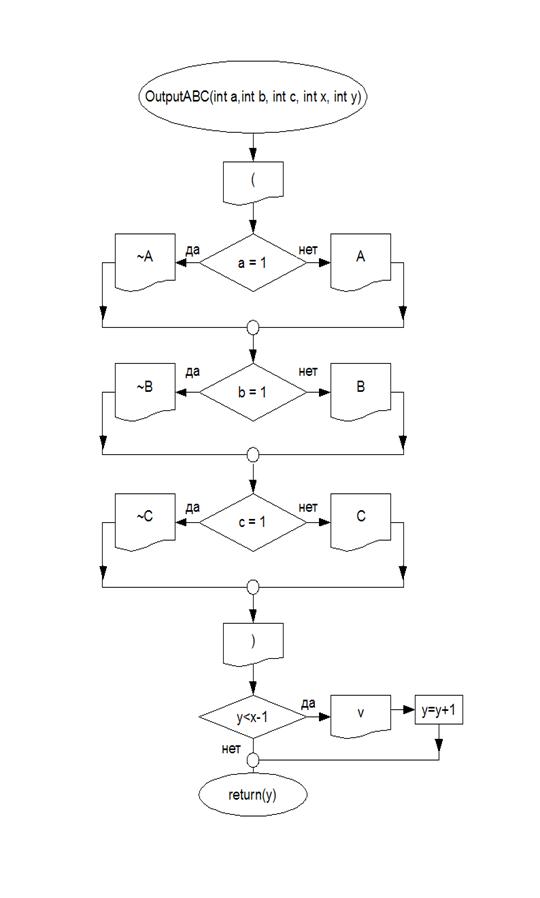
Листинг программы:
#include
#include
int FuncVolume (int &f)
{
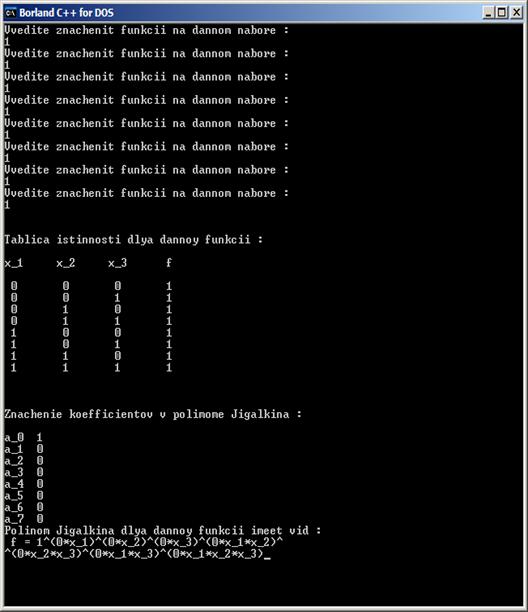
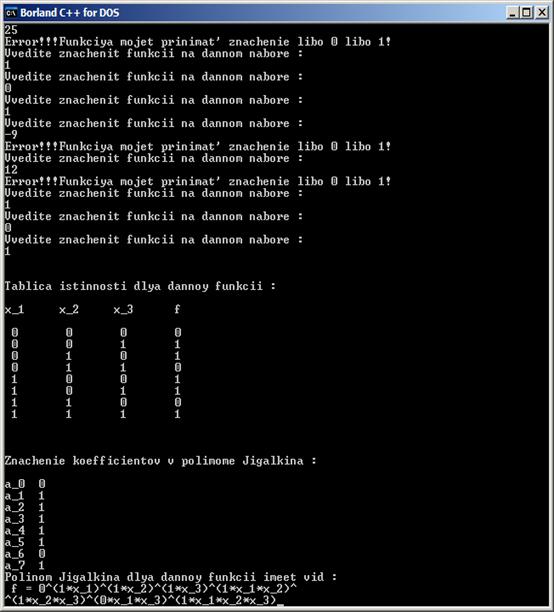
do {cout <<"Vvedite znachenit funkcii na dannom nabore :"< cin>>f; if ((f!=0)&&(f!=1)) cout<<"Error!!!Funkciya mojet prinimat' znachenie libo 0 libo 1!\n"; } while ((f!=0)&&(f!=1)); return f; } void main() { clrscr(); const N=8; int m(5); int f(N),a(N); for (int i =0; i { FuncVolume (f(i)); } a(0)= f(0); a(3)=f(0)^f(1); a(2)=f(0)^f(2); a(1)=f(0)^f(4); m(0)=f(1)^a(2)^a(3); a(5)=m(0)^f(3); m(1)=f(1)^a(1)^a(3); a(6)=m(1)^f(5); m(2)=f(1)^a(1)^a(2); a(4)=m(2)^f(6); m(3)=a(3)^a(4)^a(5); m(4)=m(2)^m(3)^a(6); a(7)=m(4)^f(7); cout<<"\n\nTablica istinnosti dlya dannoy funkcii : \n\n"; cout<<"x_1 x_2 x_3 f\n\n"; cout<<" 0 0 0 "< <<"\n 0 0 1 "< <<"\n 0 1 0 "< <<"\n 0 1 1 "< <<"\n 1 0 0 "< <<"\n 1 0 1 "< <<"\n 1 1 0 "< <<"\n 1 1 1 "< cout<<"\n\nZnachenie koefficientov v polimome Jigalkina : \n\n" ; for (i=0; i { cout<<"a_"< cout<<"Polinom Jigalkina dlya dannoy funkcii imeet vid : \n f = "< <<"^("< < getch(); } Тестирование программы: На каждом наборе вводятся единицы, то есть функция является тождественной единицей. Простейшая проверка на правильность работы программы: Так же реализована проверка на правильный ввод данных: Заключение В курсовой работе был реализован метод неопределенных коэффициентов для представления функции в виде полинома Жегалкина. По данному алгоритму на языке С++ была написана программа, результат которой был продемонстрирован. Список использованной литературы 1. Яблонский С.В. Введение в дискретную математику. — М.: Наука. — 1986 2. Н.А.Ахметова, З.М.Усманова Дискретная Математика. Функции алгебры логики учебное электронное издание – Уфа – 2004 3. Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учебное пособие. – 3-е изд., перераб. – М.: ФИЗМАТЛИТ, 2005.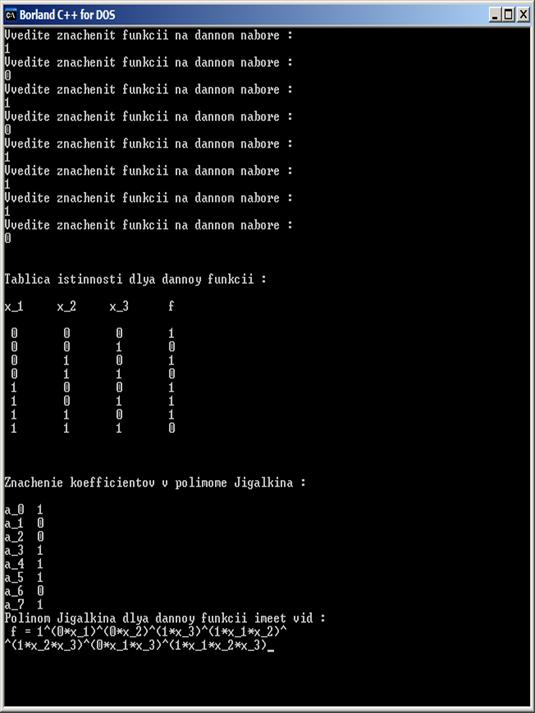
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Построение матрицы достижимости
- Построение минимального остовного дерева графа методом Прима
Пояснительная запискак курсовому проектутема: Построение минимального остовного дерева графа методом ПримаВведениеПри проектирован
- Представление бинарного дерева в виде массива
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТАФедеральное государственное образовательное учреждение высшего профессионально
- Представление булевых функций в СКНФ
Курсовая работа«Представление булевых функций в СКНФ»ВведениеВ курсе дискретной математики изучаются функции, область определения к
- Приближенное решение интегрального уравнения
В данной работе требуется с помощью методов конечно-разностных, центрально-разностных отношений и метода прогонки найти приближенное
- Приложение интегрального и дифференциального исчисления к решению прикладных задач
Федеральное Агентство по образованиюГосударственное образовательное учреждение высшего профессионального образованияМосковский Г
- Синтез дискретно-логического устройства управления электронных часов
МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИУФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТФИЛИАЛ В Г. ИШИМБА
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

