referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Построение матрицы достижимости
Цель работы:
Разработать программу на языке TURBO PASCAL, осуществляющую вычисление матрицы достижимости.
Постановка задачи:
Составить программу определения матрицы достижимости. Теоретически объяснить принцип вычисления матрицы достижимости. Представить текст программы с комментариями, а также показать ее схематически (в виде блок – схем). Проверить правильность работы программы, тем самым показать результаты тестирования. В итоге сделать выводы по проделанной работе.
Матрицы достижимости и связности
Пусть A(D) – матрица смежности ориентированного псевдографа D=(V,X) (или псевдографа G=(V,X)), где V={v1,…, vn}. Обозначим через Ak=(a(k)ij) k-ю степень матрицы смежности A(D).
Утверждение. Элемент a(k)ij матрицы Ak ориентированного псевдографа D=(V,X) (псевдографа G=(V,X)) равен числу всех путей (маршрутов) длины k из vi в vj.
Доказательство:
Для k=1 очевидно в силу построения матрицы A(D).
Пусть это справедливо для n=k-1. Т.е. в матрице Ak-1 в i-той строке на l-том месте стоит число, означающее кол-во маршрутов из vi в vl длины k−1. Столбец под номером j матрицы A содержит числа, означающие кол-во дуг (ребер) из vl в vj (l-номер строки). Тогда скалярное произведение i-той строки матрицы Ak-1 на j-тый столбец матрицы A равен сумме произведений. Каждое произведение означает кол-во путей из vi в vj, проходящих через vl на предпоследнем шаге. В сумме получается общее кол-во.
Утверждение. Для того, чтобы n-вершинный орграф D с матрицей смежности A=A(D) имел хотя бы один контур, ó чтобы матрица K=A2+A3+… An имела ненулевые диагональные элементы (следствие предыдущего).
Пусть ρ-отношение достижимости на множестве V всех вершин (неориентированного) графа G. (либо v=w, либо существует маршрут, соединяющий v и w).
Тогда
1) ρ-отношение эквивалентности;
2) vρw ó вершины v,w принадлежат одной компоненте связности;
3) для любого класса эквивалентности V1 псевдограф G1, порожденный множеством V1, является компонентой связности псевдографа G. Для орграфа: Пусть 1-отношение достижимости на множестве V всех вершин ориентированного псевдографа D. Пусть ρ2-отношение двусторонней достижимости на множестве V. (ρ2=ρ1∩ρ1-1). Тогда
1) ρ1 - рефлексивно, транзитивно;
2) ρ2 – эквивалентность на V;
3) vρ2w ó когда вершины v,w принадлежат одной компоненте сильной связности;
4) для любого класса эквивалентности V1 ориент. псевдограф D1, порожденный множеством V1, является компонентой связности ор. псевдографа G.
Число компонент связности орграфа D обозначается P(D). (для неор. - P(G).
Определение. Под операцией удаления вершины из графа (орграфа) будем понимать операцию, заключающуюся в удалении некоторой вершины вместе с с инцидентными ей ребрами (дугами).
Определение. Вершина графа, удаление которой увеличивает число компонент связности, называется точкой сочленения.
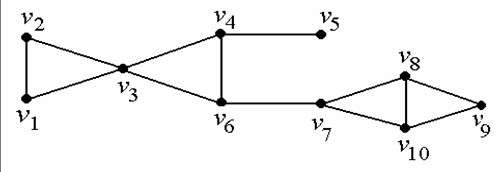
Утверждение. Если D' – орграф, полученный в результате удаления нескольких вершин из орграфа D, то A(D') получается из A(D) в результате удаления строк и столбцов, соответствующих удаленным вершинам. (Для неор. графа то же самое).
Определение. Матрицей достижимости орграфа D называется квадратная матрица T(D)=(tij) порядка n, элементы которой равны
- tij=1, если vj достижима из vi,
- tij=0, в противном случае.
Определение. Матрицей сильной связности орграфа D называется квадратная матрица S(D)=(sij) порядка n, элементы которой равны
- sij=1, если vj достижима из vi и vi достижима из vj,
- sij=0, в противном случае.
Определение. Матрицей связности графа G называется квадратная матрица S(G)=(sij) порядка n, элементы которой равны
- sij=1, если существует маршрут, соединяющий vj и vi ,
- sij=0, в противном случае.
Утверждение
Пусть G=(V,X) – граф, V={v1,…, vn}, A(G) – его матрица смежности. Тогда
S(G)=sign(E+A+A2+A3+… An-1) (E- единичная матрица порядка n). (Следует из предыдущего).
Алгоритм выделения компонент сильной связности
1. Присваиваем p=1, S1=S(D).
2. Включаем в множество вершин Vp компоненты сильной связности Dp вершины, соответствующие единицам первой строки матрицы Sp. В качестве матрицы A(Dp) возьмем подматрицу матрицы A(D), состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из Vp.
3. Вычеркиваем из Sp строки и столбцы, соответствующие вершинам из Vp. Если не остается ни одной строки (и столбца), то p- кол-во компонент сильной связности. В противном случае обозначим оставшуюся после вычеркивания срок и столбцов матрицу Sp+1, присваиваем p:=p+1 и переходим к п. 2.
Текст программы (с комментариями)
PROGRAM G_r_a_p_h;
Uses CRT;
const MaxNodes = 5; { Количество вершин в графе }
type NodePtr = 1..MaxNodes;
Element = 0..1;
AdjMatrix = Array (NodePtr,NodePtr) of Element;
var Adj : AdjMatrix; { Матрица смежностей }
Path: AdjMatrix; { Матрица достижимости }
i,j : NodePtr;
PROCEDURE P_r_o_d (A,B: AdjMatrix; var C: AdjMatrix);
{ Матрица C получает значение булевского }
{ произведения матриц A и B }
var Val : Element;
i,j,k: Integer;
BEGIN
For i:=1 to MaxNodes do
For j:=1 to MaxNodes do begin
Val:=0;
For k:=1 to MaxNodes do
Val:=Val OR (A(i,k) AND B(k,j));
C(i,j):=Val end
END;
PROCEDURE T_r_a_n_s_C_l_o_s_e (Adj: AdjMatrix; var Path: AdjMatrix);
{ Вычислени матрицы достижимости Path по }
{ заданной матрицы смежностей Adj }
var i,j,k : NodePtr;
NewProd: AdjMatrix;
AdjProd: AdjMatrix; BEGIN
AdjProd:=Adj; Path:=Adj;
For i:=1 to MaxNodes-1 do begin
P_r_o_d (AdjProd,Adj,NewProd);
For j:=1 to MaxNodes do For k:=1 to MaxNodes do
Path(j,k):=Path(j,k) OR NewProd(j,k);
AdjProd:=NewProd
end
END;
BEGIN
clrscr;
{ Ввод матрицы смежностей заданного графа }
WriteLn ('Вводите элементы матрицы смежностей по строкам:');
For i:=1 to MaxNodes do
For j:=1 to MaxNodes do begin
Write ('‚Введите Adj(',i,',',j, '): '); ReadLn (Adj(i,j)) end;
{ Вычисление и вывод матрицы достижимости }
T_r_a_n_s_C_l_o_s_e (Adj,Path);
WriteLn ('Матрица достижимости: ');
For i:=1 to MaxNodes do begin For j:=1 to MaxNodes do if i=j then Path(i,j):=1; end;
For i:=1 to MaxNodes do begin For j:=1 to MaxNodes do Write (Path(i,j),' '); WriteLn end;
readkey;
END.
Блок – схемы программы
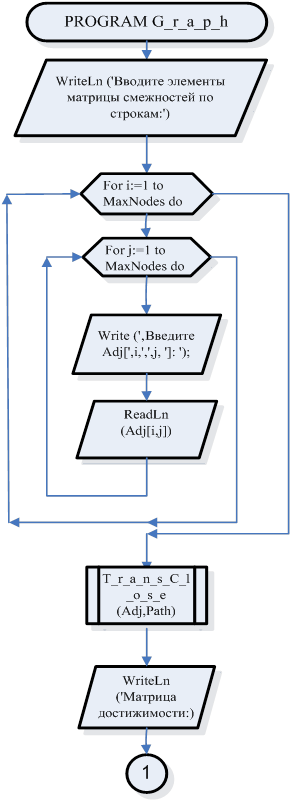
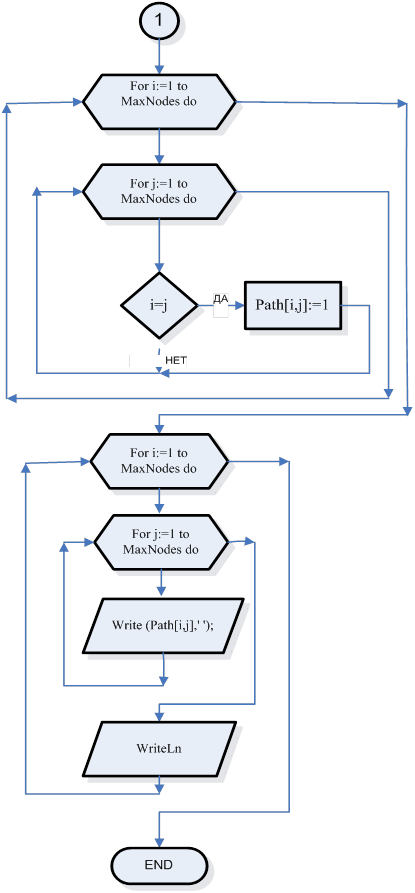
Подпрограмма, где матрица С получает значение булевского произведения матриц А и В.
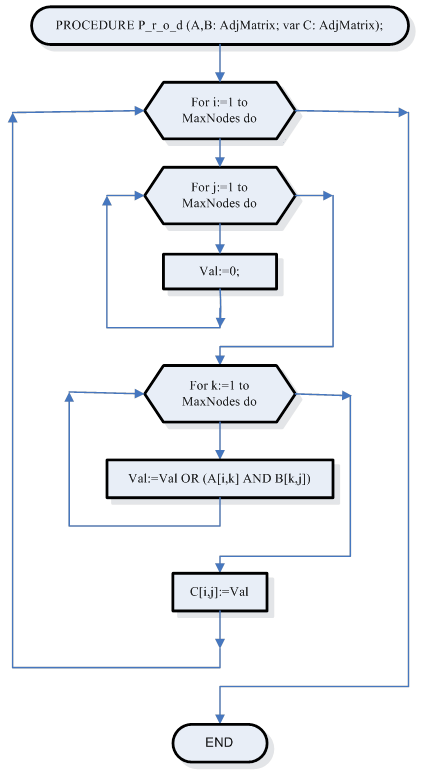
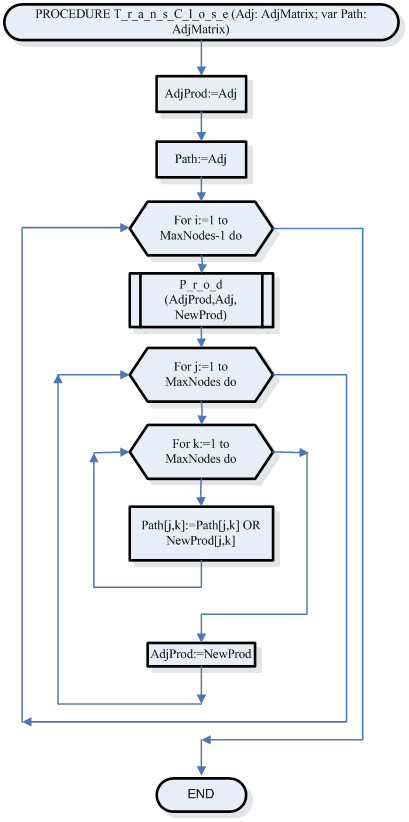
Подпрограмма для вычисления матрицы достижимости Path по заданной матрицы смежности Adj.
Результаты тестирования программы
Тест 1
Вводите элементы матрицы смежностей по строкам:
Введите Adj(1,1): 0
Введите Adj(1,2): 0
Введите Adj(1,3): 1
Введите Adj(1,4): 0
Введите Adj(1,5): 0
Введите Adj(2,1): 0
Введите Adj(2,2): 0
Введите Adj(2,3): 0
Введите Adj(2,4): 0
Введите Adj(2,5): 0
Введите Adj(3,1): 0
Введите Adj(3,2): 1
Введите Adj(3,3): 0
Введите Adj(3,4): 1
Введите Adj(3,5): 1
Введите Adj(4,1): 0
Введите Adj(4,2): 1
Введите Adj(4,3): 0
Введите Adj(4,4): 0
Введите Adj(4,5): 0
Введите Adj(5,1): 1
Введите Adj(5,2): 0
Введите Adj(5,3): 0
Введите Adj(5,4): 1
Введите Adj(5,5): 0
Матрица достижимости:
1 1 1 1 1
0 1 0 0 0
1 1 1 1 1
0 1 0 1 0
1 1 1 1 1
Тест 2
Вводите элементы матрицы смежностей по стро-кам:
Введите Adj(1,1): 0
Введите Adj(1,2): 1
Введите Adj(1,3): 0
Введите Adj(1,4): 1
Введите Adj(1,5): 0
Введите Adj(2,1): 0
Введите Adj(2,2): 0
Введите Adj(2,3): 0
Введите Adj(2,4): 0
Введите Adj(2,5): 0
Введите Adj(3,1): 1
Введите Adj(3,2): 1
Введите Adj(3,3): 0
Введите Adj(3,4): 0
Введите Adj(3,5): 0
Введите Adj(4,1): 0
Введите Adj(4,2): 0
Введите Adj(4,3): 1
Введите Adj(4,4): 0
Введите Adj(4,5): 0
Введите Adj(5,1): 1
Введите Adj(5,2): 0
Введите Adj(5,3): 0
Введите Adj(5,4): 1
Введите Adj(5,5): 0
Матрица достижимости:
1 1 1 1 0
0 1 0 0 0
1 1 1 1 0
1 1 1 1 0
1 1 1 1 1
Заключение
В результате выполнения курсовой работы была разработана программа для вычисления матрицы достижимости. В работе были решены все поставленные перед нами задачи: теоретическое объяснение принципа вычисления матрицы достижимости; представление текста программы с комментариями, а также представления ее в виде блок – схем; проверка правильности работы программы то есть представление результатов тестирования.
Программа написана на языке TURBO PASCAL, однако может быть легко переписана на любой из современных языков программирования, так как приведены довольно простые алгоритмы. Были максимально предусмотрены все возможные ошибки, которые могут возникнуть при использовании данной программы.
Список использованной литературы
1. Нефедов В.Н., Осипова В.А. // Курс дискретной математики. // М.: МАИ, 1992.
2. Кузнецов О.П., Адельсон-Вельский Г.М. // Дискретная математика для инженера. // М.: Энергоатомиздат, 1988.
3. Кук Д., Бейз Г. // Компьютерная математика. // М. Наука, 1990.
4. Бронштейн Е.М. // Множества и функции. // Методические указания. Уфа: УГАТУ. 1988.
5. Житников В. П. // Конспект лекции по дискретной математике. // Уфа: УГАТУ. 2007.
6. Павловская Т. А. Щупак Ю. А. // Учебник по практическому программированию (Бейсик, С, Паскаль). // Санкт-Петербург. 2005.