Лекции (1-18) по мат. анализу 1 семестр
По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик
van_mo_mail@mtu-net.ruили на сотовый:
8-901-7271056 спросить Ваню
екция №1Ведущая: Голубева Зоя Николаевна
Дата: вторник, 5 сентября 2000 г.
Тема: Введение
Условные обозначения:
: - так, что def – по определению
– включает ’’’ – (dnf(x))/dxn=(d/dx)((dn-1f(x))/dxn)
- следует, выполняется
- тогда и только тогда
- любой
- существует
) – пусть
! – единственный
(x) – целая часть
~ - эквивалентно
о - малое
Все R представляют десятичной дробью.
Все Q представляют конечной дробью, либо периодичной дробью.
Все иррациональные числа представляют бесконечной десятичной дробью ( не периодичной).
Рассмотрим числовую ось. Числовая ось – направленная прямая с отмеченной точкой и отмеченным масштабом.
x
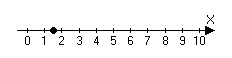
0 – отвечает за ноль.
Отрезок (0;1) отвечает за единицу
Единица за единицу.
Каждой точки х на числовой прямой отвечает некоторое действительное число. Если длинны отрезков (0;x) из заданного масштаба соизмеримы, тогда числу х отвечает рациональное число. Если не соизмеримы, то иррациональны.
Каждому R отвечает точка на числовой прямой и наоборот, каждой точке отвечает R.
Основные числовые множества.
x
![]() Отрезок: (/////////) x
Отрезок: (/////////) x
a b
Обозначается (a;b) ab
Частный случай отрезка точка
Или axb – в виде неравенства.
х
![]() Интервал: (/////////) x – множество точек на числовой прямой.
Интервал: (/////////) x – множество точек на числовой прямой.
a b
Обозначается (a;b) или в виде неравенства a x a b x a b Обозначается: (a;b) axb (a;b) a Всё это числовые промежутки. Замечание: один из концов ( а или b) может быть символом . x x Вся числовая прямая – R=(-;+) Окрестности. Определение: ε –окрестностью числа а называется множество чисел х удовлетворяющие неравенству ε>0 а-ε а а+ε Оε(а)={xR:x-a<ε} Проколотая ε окрестность – Оε(а) это множество таких чисел включающих R, и отстаёт от точки на ε и не принадлежит а. Оε(а)={xR:0<x-a<ε} а-ε а а+ε Правая ε поло окрестность точки а: О+ε(а)={xR:ax a a+ε Проколотая правая ε поло окрестность точки а: Оε(а)={xR:a Левая ε поло окрестность точки а: O-ε(a)={xR:a-ε a-ε a Проколотая, левая ε поло окрестность точки а: О-ε(а)={xR:a-ε Модуль и основные неравенства. х= 0; x=0 -x; x<0 |x| h>0 x<-h а,b R: |ab|a|+|b| а,b R: |a-b|||a|-|b|| Можно рассматривать окрестности бесконечности: О ε>0 ε О ε>0 -ε 0 О x>ε;x<-ε -ε ε Функция. Монотонность. Ограниченность. х – называется независимой переменной. у – зависимой. Функцию можно задавать равенством (у=х2) Таблицей Х1 Х2 Х3 Х4 У1 У2 У3 У4 Графиком, то есть множеством точек с координатами (x,f(x)) на плоскости: Определение f(x) монотонности: Пусть Х принадлежит области определение D ( )xD) Пусть Х подмножество в области определения в f(x). Функция у=f(x) называется: Возрастающая на Х, если для любого х1;х2 принадлежащие Х: х1 Убывающий на Х, если для любого х1;х2 принадлежащие Х: х1 3) Не убывающий на Х, если для любого х1;х2 принадлежащие Х: х1 Не возрастающая на Х, если для любого х1;х2 принадлежащие Х: х1 Определение: Ограниченность. Пусть Х включает D y=f(x) называется: Ограниченной сверху на Х если существует В, так что для любого х принадлежащего Х выполняется xR Ограниченной снизу на Х если существует А, так что для любого х принадлежащего Х выполняется Ах Ограниченной и сверху и снизу на Х если существует А,В, так что для любого х принадлежащего Х выполняется АхВ, или существует С, так что для любого х принадлежащего Х выполняется хС Лекция №2 Ведущая: Голубева Зоя Николаевна Дата: вторник, 12 сентября 2000 г. Тема: Функции Определение (сложная функция): Пусть задано D,E,G,C,R На D: y=f(x) с областью значения E На E: z=g(y) с областью значения G Тогда на множестве D определена сложная функция z=g(f(x)) с областью значения G. Тогда говорят, что g(f(x)) есть суперпозиция функций g,f. Пример: Пример z=sin ex w=arctgcos exx-lnx y=ex=f(x) z=sin y=g(y) D=R E=R+ G=(-1;1) Определение (обратной функции): Пусть существует D,E,C,R На D: y=f(x) с областью значений Е. Если для каждого у из y=f(x) найдётся единственный х, то говорят, что на множестве Е задана функция обратная к функции f(x), с областью значений D. Иными словами две функции y=f(x) и x=g(y) являются взаимно обратными если выполняется тождества: y=f(g(y)), yE y=f(g(y)), для любого уЕ x=g(f(x)), xD x=g(f(x)), для любого хD П 1)y=x3 x=3y D=R E=R 2 D=R+{0}=(0;+) E=(0;+) D=R-{0}=(-;0) E=(0;) x=-y 3 D=(-/2;/2) E=(-1;1) x=arcsiny y(-1;1); x(-/2;/2) Пусть y=f(x) D=(a;b) E=(A;B) Определение: y=f(x), nN a1=f(1) a2=f(2) an=f(n) {an} – множество значений силовой последовательности nN или аn { аn=1/n {аn}={sin1;sin2;sinn} аn=sinn аn=(-1)n/n {(-1)n}={-1;1;-1;1;-1;1…} Ограниченные последовательности. Ограниченная сверху, то есть существует В так что аnВ, для любого nN Ограниченная снизу, то есть существует А так что Аbn, для любого nN Ограниченная, то есть существует А,В так что АаnВ, для любого nN существует С>0 так что аnС, для любого nN. возрастающая an убывающая an>an+1, nN не возрастающая anan+1, nN не убывающая anan+1, nN Пределы последовательности. Определение: числа а , называется пределом числовой последовательности аn, если для любого сколь угодно малого числа ε>0, найдётся натуральный номер N такой, что для всех чисел nN выполняется модуль разности an-a<ε ε>0 N : nN an-a<ε. Lim an=0 n Примеры: Доказать, что ln(-1)2/n=0 Зададим любое ε>0, хотим чтобы (-1)n-0<ε, начиная с некоторого номера N, 1/n<ε n>1/ε N=(1/ε)+1 ε=0.01 N=(1/0.01)+1=101 |an|<0.01, если n101 * * * an=1-1/n2 lim(1-1/n2)=1 n+ Для любого ε>0 (1-1/n2)-1<ε -1/n2<ε 1/n2<ε n2>1/ε n>1/ε N=(1/ε)+1 Лекция №3 Ведущая: Голубева Зоя Николаевна Дата: среда, 13 сентября 2000 г. Тема: Последовательности Последовательность аn называется бесконечно малой , это означает, что предел этой последовательности после равен 0. an – бесконечно малая lim an=0 то есть для любого ε>0 существует N, такое что для любого n>N выполняется n+ an<ε Важные примеры бесконечно малой последовательности: 1)n=1/n Докажем, что для любого ε>0 1/n<ε 1/n<ε n>1/ε N(1/ε)+1 Докажем, что lim1/n=0 n+ 2) n= sin(1/n). Докажем, что для любого ε>0 sin(1/n)<ε, заметим, что 1/n принадлежит первой четверти, следовательно 1sin(1/n)>0, следовательно sin(1/n)<ε Следовательно 1/n 3) n=ln(1+1/n) n0; 1/n; 1+1/n1 lim ln(1+1/n)=0 n+ Докажем ln(1+1/n)<ε ln(1+1/n)<ε 1+1/n 1/n n>1/eε-1 N=(1/eε-1)+1 n=1-cos(1/n) lim(1-cos(1/n))=0 n+ Докажем ε>0 1-cos(1/n)<ε 1/n первой четверти cos первой четверти положительный 0 cos(1/n)>1-ε (считаем, что 0<ε<1) 1/n N=(1/arcos(1-ε))+1 Свойства бесконечно малой последовательности. Теорема. Сумма бесконечно малой есть бесконечно малое. nnбесконечно малое n+n – бесконечно малое. Доказательство. Дано: n- бесконечно малое ε>0 N1:n>N1n<ε n- бесконечно малое ε>0 N2:n>N2n<ε Положим N=max{N1,N2}, тогда для любого n>N одновременно выполняется оба неравенства: n<ε n+nn+n<ε+ε=2ε=ε1n>N n<ε Зададим ε1>0, положим ε=ε1/2. Тогда для любого ε1>0 N=maxN1N2 : n>N n+n<ε1 lim(n+n)=0, то n есть n+n – бесконечно малое. Теорема Произведение бесконечно малого есть бесконечно малое. n,n – бесконечно малое nn – бесконечно малое. Докозательство: Зададим ε1>0, положим ε=ε1, так как n и n – бесконечно малое для этого ε>0, то найдётся N1: n>N n<ε Возьмем N=max {N1;N2}, тогда n>N = n<ε n<ε nn=nn<ε2=ε1 ε1>0 N:n>N nn<ε2=ε1 lim nn=0 nn – бесконечно малое, что и требовалось доказать. n Теорема Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность аn – ограниченная последовательность n –бесконечно малая последовательность ann – бесконечно малая последовательность. Доказательство: Так как аn – ограниченная С>0: nNanC Зададим ε1>0; положим ε=ε1/C; так как n – бесконечно малая, то ε>0 N:n>Nn<εann=ann ε1>0 N: n>N ann=Cε=ε1 lim ann=0 ann – бесконечно малое n Замечание: в качестве ограниченной последовательности можно рассматривать const произведение постоянно. Теорема о представление последовательности имеющий конечный предел. lim an=a an=a+n n+ Последовательность an имеет конечный предел а тогда и только тогда, когда она представлена в виде an=a+n где n– бесконечно малая. Доказательство: lim an ε>0 N:n>N an-a<ε. Положим an-a=nn<ε, n>N, то есть n - бесконечно малая n+ an=a+n что и требовалось доказать Доказательство (обратное): пусть an=a+n, n – бесконечно малая, то есть n=an-a ε>0 N: n>N n=an-a<ε, то есть lim an-а n+ Теоремы о пределах числовых последовательностей. Теорема о пределе суммы: Пусть lim an=a lim bn=b lim an+n=a+b n+ n+ n+ Докозательство: an=a+n bn=b+n Сложим an+bn=a+b+n+n=a+b+nlim an+bn=a+b n+ 2) Теорема о произведение пределов: Пусть lim an=a lim bn=b lim anbn=ab n+ n+ n+ Доказательство: an=a+n bn=b+n anbn=(a+n)(b+n) anbn=ab+an+bn+nn=ab+n lim anbn=ab что и n+ требовалось доказать. Теорема о пределе частного Пусть lim an=a lim bn=b b0 lim an/bn=a/b n+ n+ n+ Доказательство: an=a+n bn=b+n так как b0, то N1: n>N1bn0 bn an/bn=an/bn-a/b+a/b=a/b+(ban-abn)/bbn=a/b+(b(a+n)-a(b+n))/b(b+n)=a/b+n/b(1+bn/b) lim an/bn=a/b n+ Лекция №4 Ведущая: Голубева Зоя Николаевна Дата: понедельник, 19 сентября 2000 г. Тема: Бесконечно большие последовательности. аn=(-1)n– не имеет предел. {bn}={1,1…} {an}={-1;1;-1;1…} – предел не существует. Бесконечно большие последовательности. an=2n N:n>N an>ε bn=(-1)n2n N:n>N bn>ε cn=-2n N:n>N cn<-ε Определение (бесконечно большие последовательности) 1) lim an=+, если ε>0N:n>N an>ε где ε- сколь угодно малое. n 2)lim an=-, если ε>0 N:n>N an<-ε n+ 3) lim an=ε>0 N:n>N an>ε n+ Последовательностью имеющий конечный пределназывают сходящимися. В противном случае последовательность называют расходящимися. Среди них есть последовательности, которые расходятся в бесконечность. О них мы говорим, что они имеют бесконечный предел. Доказательство: an=2n Берём ε>0; хотим 2n>ε n>log2ε N=(log2ε)+1 Правило формирования обратного утверждения: нужно поменять местами значки и , а знак неравенства на дополнительный. Пример: Утверждение lim an=a<aRε>0 NN:n>Nan-a<ε n Обратное утверждение aRε>0 NN: n>Nan-a<ε Всякая бесконечно большая не ограниченная. Обратное утверждение неверно. bn{2;0;2n;0;23;0….} Теорема (об ограниченной сходящейся последовательности) Пусть lim an=a< an - ограниченная n+ Доказательство: Дано: ε>0N:n>N an-a<ε Раз ε>0 возьмем ε=1 N:n>N an-a<1 a-1 Этому неравенству может быть не удовлетворять только первые N члены последовательности. N1=max{a1;a2;…an;1+a;a-1} anc, n>N Теорема (о единстве предела сходящейся последовательности). Если lim an=a <, то а- единственное. n+ Доказательство:(от противного) Предположим, что b: lim an=b и ba ε=b-a/2>0 для определенности пусть b>a N1:n>N1an-a<ε n+ N2:n>N2an-b<ε N=max{N1;N2}, тогда оба неравенства выполняются одновременно -(b-a)/2 -(b-a)/2 an-a<(b-a)/2 - b-a 0<0 – противоречие предположение, что b>a неверно. Аналогично доказывается, что b Связь между бесконечно большими и бесконечно малыми величинами. Теорема: 1)an- бесконечно большая 1/an – бесконечно малая 2)т – бесконечно малая, n0 (n>N0) 1/n – бесконечно большая Доказательство: 1)an- бесконечно большая lim an= для достаточно больших номеров n an0. Зададим любое сколько n+ угодно малое ε>0, положим ε=1/ε>0 Для ε N1:n>N1an>ε, то есть an>1/ε N=max{N1;N0} Тогда n>N 1/an<ε, то есть lim 1/an=0, то есть 1/an – бесконечно малое n+ 2)n – бесконечно малое lim n=0 n+ Дано: n0, n>N0 зададим ε>0 положим ε=1/ε>0 N1:n>N1n<ε=1/ε N=max{N0;N1}: n>N 1/n=, то есть 1/n – бесконечно большая. Основные теоремы о существование предела последовательности. Теорема Вейрштрасса: Пусть an- ограниченная и моннатонна. Тогда lim an=а< n+ Лемма. Среднее арифметическое чисел больше среднего геометрического. Равенство достигается только если все числа равны. Л По всем вопросам и по дальнейшему пополнению лекций обращаться на ящик van_mo_mail@mtu-net.ruили на сотовый: 8-901-7271056 спросить Ваню Ведущая: Голубева Зоя Николаевна Дата: вторник, 25 сентября 2000 г. Тема: Бесконечно большие последовательности Теорема: lim(1-1/n)n=1/e e=2,7183 n+ 0an=1-1/n1 nN, то есть an=(1-1/n)n- ограниченна. n+1an=n+1(1-1/n)n1=n+1(1-1/n)(1-1/n)…(1-1/n)1<(1+(1-1/n)+…+(1-1/n))/n+1=(n+1-n1/n)/n+1=n/n+1=1-1/n+1 n+1(1-1/n)n<1-1/n+1 (1-1/n)n<(1-1/n+1)n+1 an (1-1/n)n – имеет конечный предел lim(1-1/n)n=1/e n+ lim(1+1/n)n=e n+ lim1/(1+1/n)n=(n/n+1)n=(1-1/(n+1))n+1/ (1-1/(n+1))=(1/e)/1=1/e n+ lim(1/(1+1/n)n)=1/e n+ lim(1+1/n)n=e n+ Пусть дана an зададим произвольный набор натуральных чисел таких, что n1 an1,an2,…,ank,… Полученная последовательность называется под последовательностью и сходной последовательности. an=(-1)n {an}={-1;1;-1;1….} n1=2;n2=4,….,nk=2k {ank}={1,1,1,1…} Пусть последовательность an сходится, тогда последовательности lim an=a {ank} – гас и lim n+ lim ank=0 n+ Доказательство так как an – сходиться, то ε>0 N: n>N an-a<ε ank; nk>Nто есть ank-a<ε an=(-1)n – не имеет предела {a2n}={1,…,1,…,} {a2n-1}={-1,….,-1,…} имели бы тот же самый предел. Предел функции. Пусть y=f(x) определена в O(x0). Мы говорим, что функция f(x) имеет предел в при хх0 если ε>0 >0 x:0<x-x0<f(x)-b<ε lim f(x)=b xx Через окрестности это определение записывается следующим образом ε>0 >0 x0(x0)f(x)0ε(b) Если lim f(x)=0, то f(x) наз бесконечно малой при xx0. xx Замечание. Необходимо указать в каком именно процессе f(x) бесконечно малое. Надо указать к какому числу а. f(x)=x-1 1.x1 lim(x-1)=0, то есть y=x-1 бесконечно малое при x1 x1 2 x1 Пример f(x)=2x+1 x1 Докажем lim(2x+1)=3 x1 ε>0 >0 x:0<x-1<(2x+1)-3<ε (2x+1)-3<ε |x-1<ε/2 x1 Положим =ε/2 Теорема о бесконечно малом 1)(x);(x) – бесконечно малое xx0(x)+(x) – бесконечно малое при xx0 2)(x);(x) – бесконечно малое при xx0 3)Если f(x) – ограниченна в O(x0) и (x) – бесконечно малое при xx0, то f(x);(x) – бесконечно малое при xx0 Доказательство (3) Так как f(x) – ограниченна в O(x0), то С>0: xO(x0)|f(x)C; Так как (x) – бесконечно малое при хх0, то ε>0 >0 x: 0<x-x0<(x)<ε ε1>0 Положим ε=ε1/c >0 x: 0<x-x0|<f(x)(x)=f(x)a(x) x![]() Полуинтервал: (/////////) x
Полуинтервал: (/////////) x![]() (/////////) x
(/////////) x![]() ///////////////) x (-;b) или -
///////////////) x (-;b) или -![]() ///////////////) x (-;b) или -
///////////////) x (-;b) или -![]() a-ε
a-ε![]() (////////) x
(////////) x ![]() ///////) x
///////) x![]() (//////// x
(//////// x![]() x; x>0
x; x>0![]()
![]() ε(+)={xR:x>ε} (////////// x
ε(+)={xR:x>ε} (////////// x![]() ε(-)={xR:x<-ε} ///////////) x
ε(-)={xR:x<-ε} ///////////) x![]() ε()={xR:x>ε} \\\\\\) (////// x
ε()={xR:x>ε} \\\\\\) (////// xХ У 
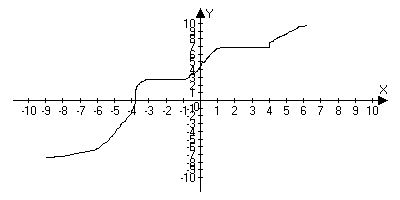
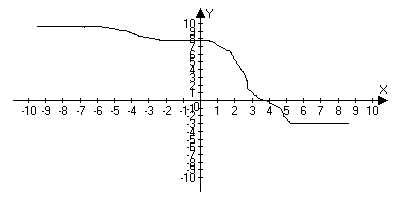
![]()
![]()
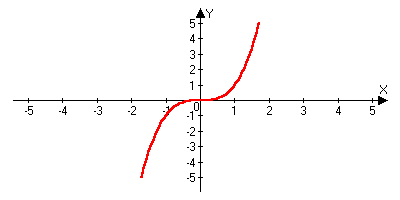 римеры:
римеры: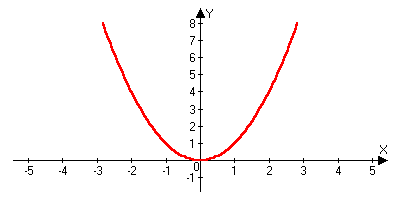 )y=x2 x=y
)y=x2 x=y 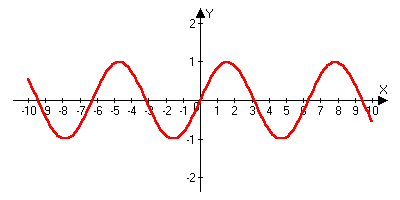 )y=sinx
)y=sinx 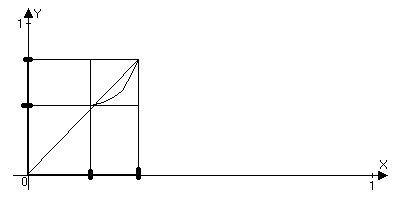
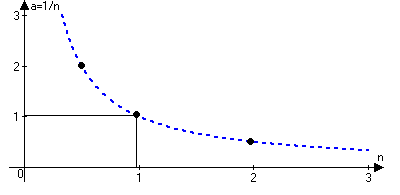 аn}={1,1/2,1/3,…,1/n,…}
аn}={1,1/2,1/3,…,1/n,…}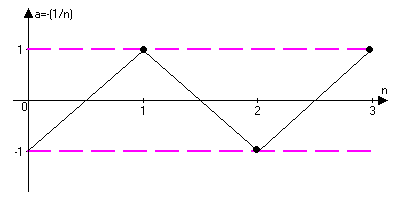
Монотонные последовательности
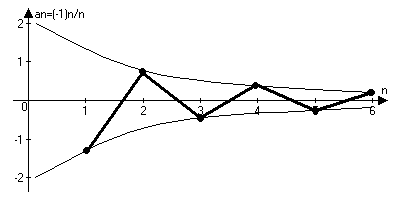 Начиная с этого номера N все числа этой последовательности попадают в ε окрестность числа а. Другими словами начиная с номера N вне интервала а-ε;а+ε может находиться не более конечного числа членов последовательности.
Начиная с этого номера N все числа этой последовательности попадают в ε окрестность числа а. Другими словами начиная с номера N вне интервала а-ε;а+ε может находиться не более конечного числа членов последовательности.Бесконечно малые последовательности
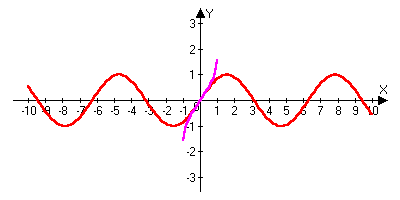
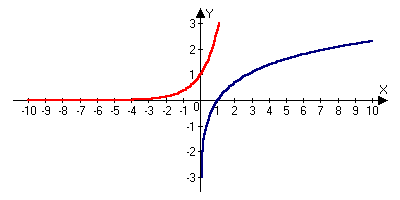 n+
n+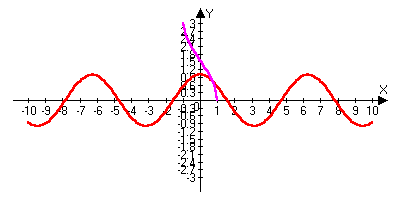
![]()
![]() N2: n>N2n<ε
N2: n>N2n<ε![]() 0(////////b/////////) x
0(////////b/////////) x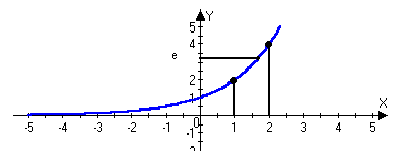
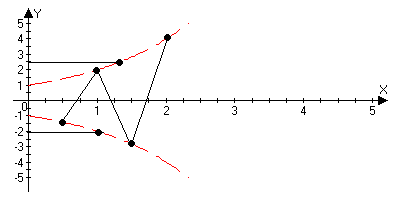
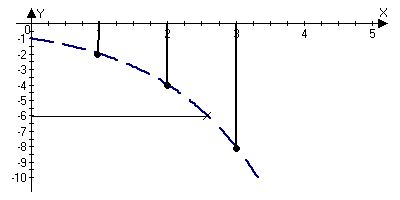

![]() an-b>-(b-a)/2
an-b>-(b-a)/2Следствие
Определение под последовательности
Теорема
Пример
Определение
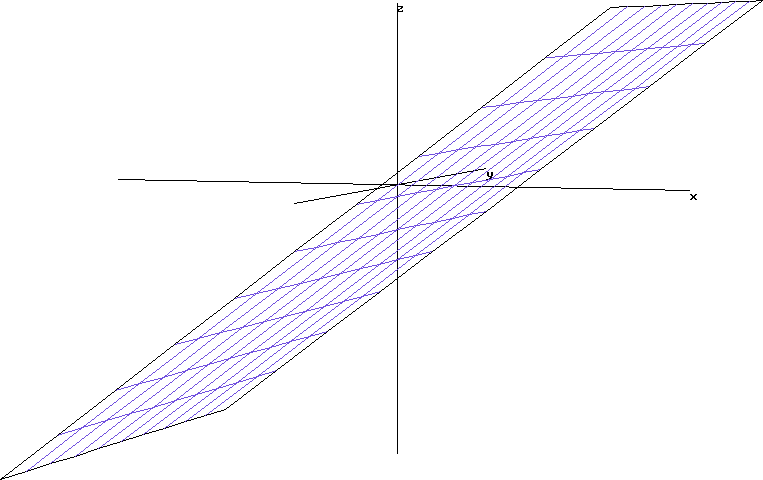
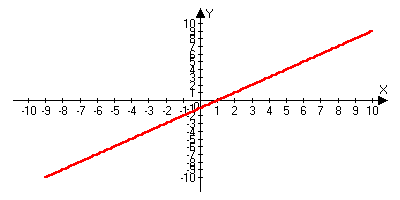
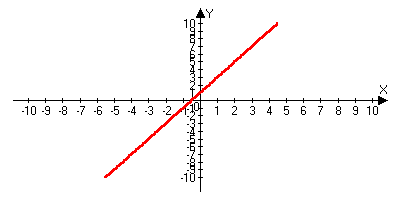 .x2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x2
.x2 lim(x-1)=1, то есть y=x-1 не является бесконечно малой при x2
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Лекции переходящие в шпоры Алгебра и геометрия
- Лекции по Математическому анализу
Аксиоматика вещественных чисел. Алгебраические свойства вещественных чисел. На множестве вещественных чисел определена операция слож
- Лекции по матану (III семестр) переходящие в шпоры
1 Двойной интегралРассмотрим в плоскости Оху замкнутую область D, ограниченную линией Г, являющейся замкнутой непрерывной кривой. z = l(P) =
- Линейное и динамическое программирование
Линейное программирование.Задача линейного оптимального планирования - один из важнейших математических инструментов, используемых в
- Линейное программирование: постановка задач и графическое решение
- Лобачевский и неевклидова геометрия
Сигулдская средняя школа N2Кронвальда 7, Сигулда, ЛатвияНеевклидова геометрия.Проект ученика 11а класса Чиркова АндреяКонсультант: Степу
- Матанализ
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

