Скачать

Сечение многогранников

Важнейшей задачей педагогической науки является совершенствование планирования процесса обучения в целом и повышение эффективности управления познавательной деятельностью учащихся.

Поиски оптимальных путей управления обучением вылились в создание новой системы учебной работы, названной программированным обучением, одними из составляющих которого являются наглядность и интерактивность обучающих программ. В настоящей курсовой работе мы рассмотрим возможность применения программированного обучения при изучении стереометрии, а именно сечения пространственных тел.

Но прежде всего необходимо отметить актуальность проблемы применения программированного (компьютерного) обучения.

В настоящее время наука и техника развиваются настолько быстро, что своевременное обобщение потока научной информации без применения кибернетических средств, представляет значительную трудность.

Не менее сложным является сообщение учащимся знаний, так как их объем из года в год увеличивается, тогда как сроки и методы обучения остаются неизменными. В связи с этим все большее число преподавателей приходит к выводу о недостаточности традиционных способов обучения и необходимости их совершенствования на основе новейших достижений науки и техники.

В школах уже появились компьютеры, но этого недостаточно. Самый лучший вариант – оснастить подобным оборудованием каждый кабинет и включить элементы работы на компьютере в учебные программы по всем предметам. Но для этого необходима техническая база. Особо надо отметить содержание самих обучающих программ, применение которых должно быть эффективным, а для этого необходимо разработать дидактический материал с учетом психолого-педагогических особенностей обучения геометрии.

В настоящее время возможно использовать элементы программированного обучения в курсе геометрии, так как большинство способов решения задач требует наглядного представления, которое можно реализовать с помощью обучающих программ. Для развития у школьников стереометрического (пространственного) представления, плоских чертежей, представляющих собой проективное изображение пространственных фигур, недостаточно необходимо создать инструмент, позволяющий интерактивно изучать стереометрию. В данном проекте мы остановимся на теме сечения пространственных тел.

Задачи проекта:

1. Изучение теоретического материала по теме проекта;

2. Создание компьютерного приложения позволяющего изучать сечения пространственных тел;

3. Оценка проделанной работы и выявление дальнейших путей развития данной темы.

Основная цель проекта: создание инструмента, позволяющего наглядно и интерактивно изучать пространственные тела и их сечения.

Промежуточные цели:

1. Разработать способ представления пространственных тел в памяти компьютера.

2. Разработать способ визуализации пространственных тел.

3. Создать алгоритм построения сечения пространственных тел.

4. Рассмотреть использование и реализацию интерактивности создаваемого приложения.

5. Разработка удобного, простого в обращении и достаточного полного интерфейса, создаваемого компьютерного приложения.

Программное обеспечение: среда программирования Delphi 7, текстовые редакторы Блокнот и MS Word, графический редактор Paint.

Глава I. Пространственные тела

1.1 Точка, прямая и плоскость в пространстве. Векторы

Понятие точка является определяющим понятием пространства, любая фигура пространства состоит из множества точек. Хранение в памяти компьютера информации о элементах пространства будем осуществлять с помощью хранения координат точек определяющих данный элемент пространства. Так для хранения информации о прямой достаточно всего двух различных точек принадлежащих этой прямой. По двум точкам задающим прямую можно составить каноническое уравнение прямой и далее оперировать этим уравнением:

, (1′)

где точки и принадлежат данной прямой. Или если использовать вектор т.е. , получим следующее уравнение прямой:

. (1′′)

Аналогично прямой, плоскость определяется тремя точками:

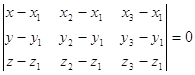, (2′)

где точки , , принадлежат данной плоскости из этой матрицы можно получить уравнение плоскости:

, (2′′)

где коэффициенты ,,, определяются следующим способом:

;

;

;

.

Причем из этих формул полезно знать, что координатами вектора нормального к данной плоскости являются соответственно коэффициенты ,,. Этот вектор направлен в полупространство правого обхода точек.

Решая совместно уравнения (1′′) и (2′′) найдем координаты точки пересечения прямой и плоскости, при условии, что прямая пересекает плоскость. Пусть плоскость задана тремя точками: , , , а прямая задана двумя точками: и , тогда координаты точки пересечения находятся по формулам:

,

где , причем если , то ; (1x)

,

где , причем если , то ; (1y)

,

где , причем если , то . (1z)

В этих формулах координаты вектора для прямой вычисляется следующим образом: .

1.2 Преобразования пространства

Для реализации интерактивности изучения пространственных тел необходимо реализовать возможность перемещения, поворота и масштабирования, а для этого необходимо изменять координаты точек фигур по соответствующему закону. Рассмотрим три преобразования которые переводят каждую точку в точку :

1. Перемещение (параллельный перенос на вектор ).

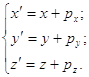(1p)

2. Поворот вокруг прямой на угол . Поворот будем осуществлять вокруг одной из осей координат.

а) вокруг оси OX:

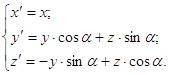(2px)

б) вокруг оси OY:

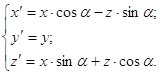(2py)

в) вокруг оси OZ:

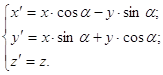(2pz)

3. Масштабирование с коэффициентом .

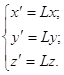(3p)

1.3 Пространственные тела

Как уже говорилось, в памяти компьютера пространственные тела будем хранить в виде координат точек определяющих эти тела. Рассмотрим далее, как хранить те или иные виды пространственных тел и рассмотрим основные способы создания фигур. При описании многогранников необходимо задание координат всех вершин многогранников, а также описание порядка обхода каждой грани. Удобно описывать обход граней почасовой стрелке наблюдая многогранник из вне, тогда нормальный вектор к грани, заданный тройкой следующих подряд вершин, будет направлен из многогранника. Это свойство удобно использовать при визуализации выпуклых многогранников, об этом будет рассказано позднее. С многогранниками все понятно, а как описывать поверхности второго порядка (поверхности вращения, конические поверхности, цилиндрические поверхности, эллипсоид, гиперболоид, параболоид). Их можно представить в виде многогранника с большим количеством граней, и чем больше количество граней, тем точнее приближение. Этот метод является универсальным, он позволяет описывать комбинированные пространственные тела, но не позволяет изучать алгебраические кривые, которые получаются при построении сечений. Приведем общую структуру файла, описывающего многогранник. Файл представляет собой обычный текстовый документ.