Расчет параметров ступенчатого p-n перехода (zip 860 kb)
Министерство образования Российской Федерации
Орловский Государственный Технический Университет
Кафедра физики
КУРСОВАЯ РАБОТА
на тему: «Расчет параметров ступенчатого
p-n перехода»
Дисциплина: «Физические основы микроэлектроники»
Выполнил студент группы 3–4
Сенаторов Д.Г.
Руководитель:
Оценка:
Орел. 2000
Орловский Государственный Технический Университет
Кафедра: «Физика»
ЗАДАНИЕ НА курсовую работу
Студент: Сенаторов Д.Г. группа 3–4
Тема: «Расчет параметров ступенчатого p-n перехода»
Задание: Рассчитать контактную разность потенциалов jk в p-n-переходе.
Исходные данные для расчета приведены в таблице №1.
Таблица 1. Исходные данные.
| Наименование параметра | Единицы измерения. | Условное обозначение | Значение в единицах системы СИ |
| Абсолютная величина результирующей примеси в эмиттере | м-3 | NЭ | 1,5 |
| Абсолютная величина результирующей примеси в базе | м-3 | NБ | 1,8 |
| Диэлектрическая постоянная воздуха | Ф/м | e0 | 8,85 |
| Заряд электрона | Кл | e | 1,6 |
| Относительная диэлектрическая проницаемость полупроводника | Ф/м | e | 16 |
| Постоянная Больцмана | Дж/К | k | 1,38 |
| Равновесная концентрация дырок в n-области | м-3 | pn0 | 1010 |
| Равновесная концентрация дырок в p-области | м-3 | np0 | 1,1 |
| Собственная концентрация носителей заряда | м-3 | ni | 5 |
| Температура окружающей среды | K | T | 290 |
ОГЛАВЛЕНИЕ.
ВВЕДЕНИЕ 4.
ЧАСТЬ I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 6.
1.1 Понятие о p-n переходе 6.
1.2 Структура p-n перехода 10.
1.3 Методы создания p-n переходов 15.
1.3.1 Точечные переходы 15.
1.3.2 Сплавные переходы 16.
1.3.3 Диффузионные переходы 17.
1.3.4 Эпитаксиальные переходы 18.
1.4 Энергетическая диаграмма p-n перехода в равновесном
состоянии 20.
1.5 Токи через p-n переход в равновесном состоянии 23.
1.6 Методика расчета параметров p-n перехода 26.
1.7 Расчет параметров ступенчатого p-n перехода 29.
ЧАСТЬ II. Расчет контактной разности потенциалов jk в p-n-переходе 31.
ЗАКЛЮЧЕНИЕ 32.
ПРИЛОЖЕНИЕ 33.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 35.
ВВЕДЕНИЕ.
Полупроводники могут находиться в контакте с металлами и некоторыми другими материалами. Наибольший интерес представляет контакт полупроводника с полупроводником. Этот интерес вызван следующими двумя обстоятельствами. В случае контакта метал–полупроводник выпрямляющими свойствами контакта можно управлять с помощью только одной из половин контакта, а именно, со стороны полупроводника. Это видно хотя бы из того факта, что весь запирающий (или антизапирающий(1)) слой лежит в полупроводниковой области и его толщину, а значит, и ток можно регулировать концентрацией носителей n0, т.е. выбором типа кристалла, легированием полупроводника, температурой, освещением и т.д. Второе обстоятельство заключается в том, что практически поверхности металла и полупроводника никогда не образуют идеального контакта друг с другом. Всегда между ними находятся адсорбированные атомы или ионы посторонних веществ. Адсорбированные слои экранируют внутреннюю часть полупроводника так, что фактически они определяют свойства выпрямляющих контактов или, во всяком случае, существенно влияют на них.
В случае контакта полупроводник–полупроводник, оба недостатка отсутствуют т.к. в большинстве случаев контакт осуществляют в пределах одного монокристалла, в котором половина легирована донорной примесью, другая половина – акцепторной. Существуют и другие технологические методы создания электронно-дырочного перехода, которые будут рассмотрены в данной курсовой работе. Кроме того, целью предпринимаемого исследования является определение основных параметров и характеристик, а также физических процессов, лежащих в основе образования и функционирования p-n-перехода для ответа на основной вопрос данной работы: «Какова ширина p-n-перехода?» при заданных исходных параметрах.
В третьей части данной работы будет предпринята попытка объяснить особенности поведения электрона с учетом спина во внешнем электрическом поле, введено понятие тонкой структуры.
ЧАСТЬ I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ.
1.1 Понятие о p-n переходе.
Основным элементом большой группы полупроводниковых приборов является электронно-дырочный переход. Такой переход представляет собой область между двумя полупроводниками разного типа проводимости, объединенную основными носителями заряда. В зависимости от характера распределения концентрации примеси в объединенном p-n слое переходы бывают ступенчатыми (резкими) и плавными.
В плавных p-n-переходах изменение концентрации донорных (Nd), и акцепторных (Na) примесных атомов происходит на расстоянии, сравнимом с шириной обеднённого слоя или превышающем её. В резких p-n-переходах изменение концентрации примесных атомов от Nd до Na происходит на расстоянии, меньшем ширины обеднённого слоя (8). Резкость границы играет существенную роль, т.к. в плавном p-n-переходе трудно получить те вентильные свойства, которые необходимы для работы диодов и транзисторов (4).
На рис. 1.1 представлено распределение зарядов в полупроводниках при плавном и резком изменении типа проводимости.
При плавном изменении типа проводимости (рис. 1.1.а) градиент концентрации(2) результирующей примеси ![]() мал, соответственно малы и диффузионные токи(3) электронов и дырок.
мал, соответственно малы и диффузионные токи(3) электронов и дырок.
Эти токи компенсируются дрейфовыми токами(4), которые вызваны электрическим полем связанным с нарушением условия электрической нейтральности:
n + Na = p + Nd, (1.1.1)
где n и p – концентрация электронов и дырок в полупроводнике:
Na, Nd – концентрация ионов акцепторной и донорной примесей.
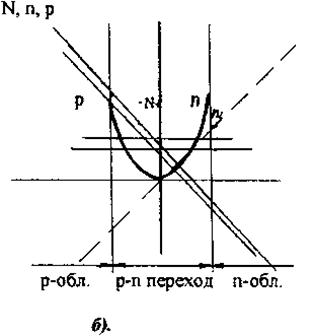
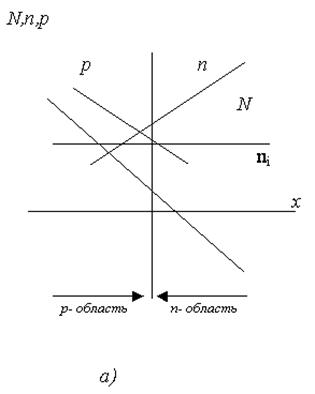
Рисунок 1.1 Распределение примеси и носителей заряда в полупроводнике при изменении типа проводимости: (а) плавное изменение типа проводимости; (б) резкое изменение типа проводимости.
Для компенсации диффузионных токов достаточно незначительного нарушения нейтральности, и условие (1.1.1) можно считать приближенно выполненным.
Условие электронейтральности свидетельствует о том, что в однородном полупроводнике независимо от характера и скорости образования носителей заряда в условиях как равновесной, так и не равновесной концентрации не могут иметь место существенные объемные заряды в течении времени, большего (3-5)τε (τε≈10-12 с), за исключением участков малой протяжённости:
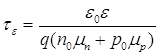
где τε – время диэлектрической релаксации; ε0 – диэлектрическая постоянная воздуха; ε – относительная диэлектрическая проницаемость полупроводника; q – заряд носителя заряда (электрона); n0, p0 – равновесные концентрации электронов и дырок в полупроводнике; μn, μp – подвижность электронов и дырок в полупроводнике.
При резком изменении типа проводимости (рис. 1.1.б) диффузионные токи велики, и для их компенсации необходимо существенное нарушение электронейтральности (1.1.1).
Изменение потенциала по глубине x полупроводника происходит по экспоненциальному закону: 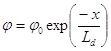 . Глубина проникновения электрического поля в полупроводник, Ld, называется дебаевской длиной и определяется из уравнения:
. Глубина проникновения электрического поля в полупроводник, Ld, называется дебаевской длиной и определяется из уравнения:
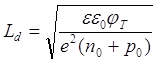 ,
,
где ![]() - температурный потенциал.
- температурный потенциал.
При этом электрическая нейтральность существенно нарушается, если на дебаевской длине изменение результирующей концентрации примеси велико.
Таким образом нейтральность нарушается при условии:
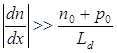 (1.1.2)
(1.1.2)
В состоянии термодинамического равновесия при отсутствии вырождения(5) справедлив закон действующих масс:
![]() (1.1.3)
(1.1.3)
При условии (1.1.3) правая часть (1.1.2) достигает минимума при ![]() поэтому условие существования перехода (условие существенного нарушения нейтральности) имеет вид:
поэтому условие существования перехода (условие существенного нарушения нейтральности) имеет вид:
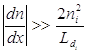 , (1.1.4)
, (1.1.4)
где 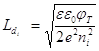 –дебаевская длина в собственном полупроводнике.
–дебаевская длина в собственном полупроводнике.
Переходы, в которых изменение концентрации примеси на границе слоев p- и n-типа могут считаться скачкообразными ![]() называются ступенчатыми.
называются ступенчатыми.
В плавных переходах градиент концентрации примеси конечен, но удовлетворяет неравенству(1.1.4).
Практически ступенчатыми могут считаться p-n-переходы, в которых изменение концентрации примеси существенно меняется на отрезке меньшем Ld.
Такие переходы могут быть полученными путем сплавления, эпитаксии.
По отношению к концентрации основных носителей в слоях p- и n-типа переходы делятся на симметричные и несимметричные.
Симметричные переходы имеют одинаковую концентрацию основных носителей в слоях (pp ≈ nn). В несимметричных p-n-переходах имеет место различная концентрация основных носителей в слоях (pp >> nn или nn >> pp), различающаяся в 100–1000 раз (3).
1.2 Структура p-n-перехода.
Наиболее просто поддаются анализу ступенчатые переходы. Структура ступенчатого перехода представлена на рис. 1.2. Практически все концентрации примесей в p- и n-областях превышают собственную концентрацию носителей заряда ni. Для определения будем полагать, что эмиттером является p–область, а базой n–область. В большинстве практических случаев выполняется неравенство
![]()
где ![]() и
и ![]() -результирующие концентрации примеси в эмиттере и базе.
-результирующие концентрации примеси в эмиттере и базе.
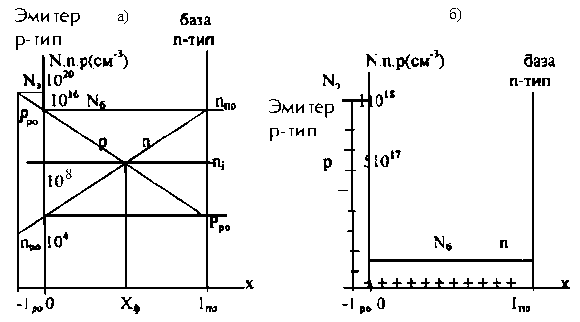 |
Рисунок 1.2 соответствует кремниевому переходу (ni ≈ 1010 см-3 ) при комнатной температуре (Т=290К) с концентрацией примеси
Рисунок 1.2 Распределение примеси и носителей заряда в ступенчатом P-N переходе: (а)- полулогарифмический масштаб; (б)- линейный масштаб.
В глубине эмиттера и базы концентрация основных носителей заряда практически совпадает с результирующей концентрацией примеси:
pро =Nэ, nnо=NБ, (1.2.1)
а концентрация не основных носителей определяется законом действующих масс:
nр0=ni/pр0=ni/Nэ (1.2.2.а)
pn0=ni/nn0=ni/NБ (1.2.2.б)
Индексы «p» и «n» соответствуют p- и n-областям, а индекс «0» соответствует состоянию термодинамического равновесия. Следует отметить, что концентрация не основных носителей в базе больше чем в эмиттере (а при Nэ>>NБ много больше). На рис. 1.2.а распределение примесей и носителей заряда представлено в полулогарифмическом масштабе.
Переход занимает область –lр0 < x < ln0. Конечно границы перехода x=-lp0 и x=ln0 определены в некоторой степени условно, так как концентрация основных носителей изменяется плавно. Тем не менее, из рисунка видно, что уже на небольшом расстоянии от границ внутри перехода выполняется равенство:
P<
n<
Неравенства (1.2.3) выполняется во всем p-n-переходе.
На рис. 1.2.б распределение концентрации носителей и примесей заряда изображены в линейном масштабе. Из рисунка видно, что в эмиттерной области перехода (-lp0 рэ = -lNэ. В базовой области перехода (0 pБ=lNб. Для n-области основными носителями являются электроны, для p-области дырки. Основные носители возникают почти целиком вследствие ионизации донорных и акцепторных примесей. Помимо основных носителей эти области содержат неосновные носители: n-область - дырки (pno), p-область –электроны (nро). Их концентрацию можно определить, пользуясь законом действующих масс: nno∙Pno=pno∙nno=ni2. При nno=ppo=1022 м-3 и ni=1019 м-3 (для Ge) получаем pno=nро=1016 м. Таким образом, концентрация дырок в p-области на шесть порядков выше концентрации их в n-области, точно также концентрация электронов в n-области на шесть порядков выше их концентрации в p-области. Т.к. концентрация дырок в области p выше, чем в области n, то часть дырок в результате диффузии перейдет в n- область, где в близи границы окажутся избыточные дырки, которые будут рекомбинировать с электронами. Соответственно в этой зоне уменьшается концентрация свободных электронов, и образуются области нескомпенсированных положительных ионов донорных примесей. В p-области уход дырок из граничного слоя способствует образованию областей с нескомпенсированными отрицательными зарядами акцепторных примесей, созданными ионами. Подобным же образом происходит диффузионное перемещение электронов из n-слоя в p-слой. Однако в связи с малой концентрацией электронов по сравнению с концентрацией дырок перемещением основных носителей заряда высокоомной области в первом приближении пренебрегают. Перемещение происходит до тех пор, пока уровни Ферми обоих слоев не уравняются (4). б) в) Рисунок 1.3 Физические процессы в полупроводнике: (а) – плоскость физического перехода; (б) – распределение концентрации акцепторной и донорной примеси в полупроводнике; (в) – объёмный заряд. На рис. 1.3.б, показано изменение концентрации акцепторных и донорных атомов при перемещении вдоль оси Х перпендикулярной плоскости. Неподвижные объемные заряды создают в p-n-переходе контактное электрическое поле с разностью потенциалов, локализованное в области перехода и практически не выходящее за его пределы. Поэтому вне этого слоя, где поля нет, свободные носители заряда перемещаются хаотично и число носителей, ежесекундно наталкивающихся на слой объемного заряда, зависит только от их концентрации и скорости их теплового движения, которое подчиняется классической статистики Максвелла-Больцмана. На рис. 1.3.в показаны неподвижные объемные заряды, образовавшиеся в p-n-переходе. Неосновные носители - электроны из p-области и дырки из n-области, попадая в слой объемного заряда подхватываются контактными полем Vк и переносятся через p-n переход. Другие условия складываются для основных носителей. При переходе из одной области полупроводника в другую они должны преодолевать потенциальный барьер qVк, сформировавшийся в p-n-переходе. Для этого они должны обладать кинетической энергией движения вдоль оси Х, не меньшей qVк. На первых порах, после мысленного приведения p- и n-областей в контакт, потоки основных носителей значительно превосходят потоки неосновных носителей. Но по мере роста объемного заряда увеличивается потенциальный барьер p-n-перехода, и потоки основных носителей резко уменьшаются. В тоже время потоки неосновных носителей не зависят от qVk и остаются неизменными. Поэтому относительно скоро потенциальный барьер достигает такой высоты, при котором потоки основных носителей сравниваются с потоками неосновных носителей. Это соответствует установлению в p-n-переходе состояния динамического равновесия. Из рис. 1.3.а видно, что в некоторой области Х=Хф концентрация электронов и дырок одинакова: n0(Хф) = p0(Хф) = n Эта плоскость называется плоскостью физического перехода в отличие от плоскости металлургического (или технологического) перехода Х=0, где результирующая концентрация примеси равна нулю. В симметричных переходах плоскости физического и металлургического переходов совпадают. Электронно-дырочные переходы в зависимости от технологии изготовления разделяются на точечные, сплавные, диффузионные, эпитаксиальные, планарные и другие.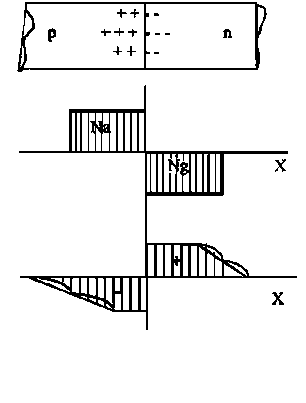 а)
а)
1.3 Методы создания p-n-переходов.
1.3.1 Точечные переходы.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Расчет погрешности вольтметра
- Расчет полевого транзистора
- Расчет полупроводникового выпрямителя с фильтром и транзисторного усилителя
- Расчет радиопередатчика с ЧМ модуляцией
- Расчет радиорелейной линии связи прямой видимости
ЗАДАНИЕ НА КУРСОВУЮ РАБОТУПривести краткую характеристику используемой аппаратуры и основные технические данные.Выбрать число узлов
- Расчет различных электрических цепей
1. РАСЧЁТ ИСТОЧНИКА ОПОРНОГО НАПРЯЖЕНИЯ Исходные данные для расчета приведены в табл. 1.1 Таблица 1.1 Расчётные данные , В, С10.51735 Исходя из
- Расчет силового трансформатора
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

