Разработка пакета программ для расчета фазированной антенной решетки
1. Обзор литературных источников
1.1 Метод наводимых ЭДС
1.2 Метод парциальной диаграммы направленности
1.3 Методы на основе теории бесконечных периодических структур
2. Расчет полевых и импедансных характеристик ФАР
2.1 Входное сопротивление элемента бесконечной периодической линейной решетки
2.2 Расчет взаимного сопротивления полосковых излучателей в составе бесконечной линейной решетки
2.3 Расчет взаимного сопротивления в двумерной плоской ФАР
2.4 Расчет входного сопротивления излучателя с учетом взаимных связей
2.5 Определение полевых характеристик ФАР
3. Программы для расчета характеристик ФАР
3.1 Общие сведения
3.2 Программа для расчета полевых и импедансных характеристик ФАР
3.2.1 Описание применения
3.2.2 Методика испытаний
3.2.3 Руководство пользователя
3.2.4 Описание программы
3.3 Программа для характеристик ФАР в полосе частот
3.3.1 Описание применения
3.3.2 Методика испытаний
3.3.3 Руководство пользователя
3.3.4 Описание программы
3.4 Программа для расчета входного сопротивления изолированного излучателя
3.4.1 Описание применения
3.4.2 Методика испытаний
3.4.3 Руководство пользователя
3.4.4 Описание программы
3.5 Программа для расчета взаимного сопротивления между излучателями
3.5.1 Описание применения
3.5.2 Методика испытаний
3.5.3 Руководство пользователя
3.5.4 Описание программы
4. Результаты расчетов
4.1 Взаимное сопротивление
4.2 Диаграмма направленности ФАР
4.3 Частотные характеристики ФАР
5. Технико-экономическое обоснование дипломной работы
5.1 Краткая характеристика работы
5.2 Определение затрат на создание программы
5.2.1 Расходы по оплате труда разработчиков программы
5.2.2 Среднечасовая оплата разработчика
5.2.3 Затраты по оплате машинного времени
5.2.4 Общие затраты на создание программы
6. Безопасность и экологичность дипломной работы
6.1 Краткая характеристика работы
6.2 Безопасность проекта
6.2.1 Электробезопасность рабочего места
6.2.2 Пожаробезопасность рабочего места
6.2.3 Микроклимат рабочего места
6.2.4 Освещенность рабочего места
6.2.5 Шумы и вибрации на рабочем месте
6.3 Эргономичность проекта
6.3.1 Рабочее место оператора ЭВМ
6.3.2 Оценка качества программных средств
6.4 Экологичность проекта
6.5 Особенности проектирования антенно-фидерных устройств к воздействию сильных электромагнитных излучений. Возможный характер повреждений
6.5.1 Экранирование
6.5.2 Фильтрация
6.5.3 Заземление
Заключение
Приложение 1
Библиографический список
Аннотация
В дипломной работе на основе метода бесконечных периодических структур был разработан пакет программ, позволяющий рассчитать полевые и импедансные характеристики плоской двумерной фазированной антенной решетки (ФАР), выполненной из полосковых вибраторов или резонансных излучателей на многослойном диэлектрической подложке, с учетом и без учета взаимной связи между излучателями как на фиксированной частоте, так и в полосе частот. Кроме того, пакет включает в себя программу для расчета взаимного сопротивления между излучателями и программу для расчета входного сопротивления изолированного излучателя.
Были произведены расчеты зависимости взаимного сопротивления от расстояния между излучателями при различных диэлектриках, характерисик ФАР в полосе частот при различных диэлектриках и количества излучателей в решетке.
Введение
Фазированные антенные решетки (ФАР) благодаря возможности быстрого и гибкого изменения амплитудно-фазового распределения в излучающей структуре нашли широкое применение в радиотехнических системах связи, локации и навигации.
Элементная база современных ФАР весьма разнообразна: это и традиционные вибраторы, и щелевые излучатели, рупоры, спирали, зеркальные антенны и т.д. Особое место в этом перечне занимают полосковые излучатели. Применение интегральной технологии при их изготовлении позволяет удовлетворить весьма жестким требованиям к электродинамическим, аэродинамическим, габаритным, весовым, экономическим, конструктивным и другим параметрам.
Развитие и усложнение ФАР привело к разработке новых и усложнению известных методов расчета основных характеристик. Конструирование и расчет антенн значительно усложнились из-за увеличения числа параметов, определяющих характеристики антенн, а также из-за стремления оптимизировать характеристики или более точно их рассчитать.
В антенных решетках имеет место сложное явление взаимодействия излучателей, проявляющееся в изменении направленности и входного сопротивления излучателя при его включении в ФАР. Взаимная связь вызывает изменение входного сопротивления каждого элемента, что приводит к рассогласованию и отражению энергии в фидерной линии обратно к источнику. Резкое рассогласование может вызвать эффект ослепления, когда практически прекращаются излучение и прием электромагнитных волн. Взаимное влияние приводит также к изменению фазового и амплитудного распределения по антенным элементам. Это в свою очередь приводит к изменению диаграммы направленности, КНД, искажению поляризационных характеристик.
В настоящее время интенсивно разрабатывается теория учета взаимных связей в антенных решетках. Инженерные методы расчета взаимодействия излучателей в составе ФАР известны только для некоторых типов антенн. Учет этого взаимодействия, изменяющегося при управлении фазовым распределением, в значительной мере затрудняет расчет ФАР.
Одним из методов, позволяющих учитывать взаимные связи в антенных решетках, является метод бесконечных периодических структур, рассмотренный в (1, 2). В этом методе сначала рассчитывают входные сопротивления излучателей путем решения интегрального уравнения Фредгольма, ядром которого является тензорная функция Грина областей, частично заполненных диэлектриком. Затем методом Галеркина находятся взаимные сопротивления между излучателями и далее все остальные импедансные и полевые харктеристики ФАР. Однако использование этого метода было ограничено из-за сложности расчетов. В настоящее время при широком распространении ПЭВМ эта задача упростилась.
Целью данной дипломной работы является разработка программы для ПЭВМ, позволяющей использовать вышеописанный метод специалистам, работающим в данной области радиотехники.
1. Обзор литературных источников
Прогресс техники антенных решеток стимулировал рост числа теоретических работ, посвященных ислледованию электродинамических характеристик ФАР. Элементарная теория антенных решеток рассматривается в (3, 4). Здесь полагается, что решетка представляет совокупность независимых индивидуальных излучателей, а характеристики излучения ФАР зависят лишь от пространственного расположения отдельных излучателей, а также от распределения амплитуд и фаз токов, заданных на излучателях.
Наряду с этим, в работах (5, 6, 7) приводятся различные методы учета взаимного влияния между излучателями в антенных решетках. Кратко охарактеризуем эти методы.
Возможны два способа оценки взаимной связи между элементами антенной решетки. Первый способ состоит в оценке изменения входного сопротивления элемента за счет взаимного влияния. Второй способ состоит в оценке изменения диаграммы направленности элемента, изолированного от влияния соседних элементов. Для нахождения взаимных сопротивлений существует множество методов как точных, так и приближенных. Кроме этого, все методы можно рассматривать с точки зрения поэлементного подхода, который полезен при анализе решеток малых размеров и подхода на основе бесконечных периодических структур, применяемого в случае больших решеток.
1.1 Метод наводимых ЭДС
Одним из методов поэлементного подхода является метод наводимых ЭДС, подробно рассмотренный в (5). Систему излучателей представляют эквивалентным четырехполюсником. Например, в простейшем случае, когда рассматривается два связанных вибратора, схема их замещения выглядит как на рис. 1.1.
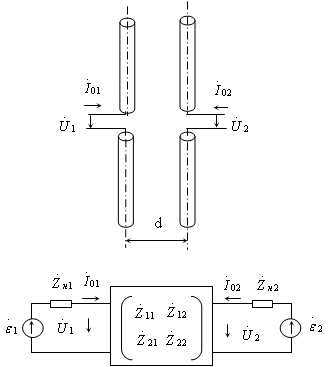
Рис. 1.1 Связанные вибраторы и их схема замещения
Диагональные элементы в матрице сопротивлений ![]() и
и ![]() представляют собственные сопротивления вибраторов. Недиагональные элементы
представляют собственные сопротивления вибраторов. Недиагональные элементы ![]() и
и ![]() являются взаимными сопротивлениями, учитывающими электромагнитную связь между вибраторами. Взаимные сопротивления равны, если среда между излучателями изотропна. Для схемы замещения может быть записано следующая система уравнений Кирхгофа:
являются взаимными сопротивлениями, учитывающими электромагнитную связь между вибраторами. Взаимные сопротивления равны, если среда между излучателями изотропна. Для схемы замещения может быть записано следующая система уравнений Кирхгофа:
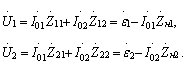 (1.1)
(1.1)
Известно, что если проинтегрировать поток вектора Пойтинга по бесконечно удаленной поверхности, охватывающей все элементы антенной решетки, то это даст возможность вычислить величину активной мощности, излучаемой всеми антеннами, а вместе с тем и активные составляющие собственных сопротивлений каждой антенны антенны и активные составляющие взаимнх сопротивлени между ними. Реактивная составляющая сопротивлений определяется по известной частотной зависимости активной составляющей.
1.2 Метод парциальной диаграммы направленности
Другим методом исследования взаимной связи, который подробно излагается в (7), является метод парциальной диаграммы направленности. Этот метод предполагает исследование диаграмм направленности и коэффициентов усиления излучателей в решетке.
Когда какой-либо излучатель антенной решетки находится в окружении остальных элементов, нагруженных на пассивные сопротивления, невозбужденные элементы также проявляют свое участие в излучении решетки. Измеренная при этом парциальная диаграмма направленности излучателя позволяет:
а) в случае возбуждения всех излучателей антенной решетки больших, но конечных размеров суперпозицией таких диаграмм получить истинную ДН решетки,
б) измеренную парциальную диаграмму можно использовать для вычисления действующего входного сопротивления или соответствующего ему коэффициента отражения, что особенно эффективно при применении к решеткам со сложными излучателями, когда теоретический анализ оказывается затруднительным.
Это метод может оказаться весьма полезным при практическом исследовании взаимного влияния в АР или при проверке теоретически полученных результатов.
1.3 Методы на основе теории бесконечных периодических структур
Для анализа больших эквидистантных АР разработан целый ряд методов, суть которых заключается в том, что АР заменяют бесконечной открытой периодической структурой и анализ поля проводят в единичной периодической ячейке такой структуры. Важным преимуществом такого подхода является то, что решение необходимо искать только для одной периодической ячейки АР, что позволяет найти достаточно точное решение при невысоком порядке решаемых уравнений.
Метод спектрального анализа, рассмотренный подробно в (6), применим в основном для эквидистантных АР, составленных из одинаковых излучателей. Мощным средством теоретического исследования таких периодических структур является аппарат рядов Фурье и дискретного преобразования Фурье (ДПФ).
Основным недостатком следует считать невозможность учета конечных размеров АР и краевых эффектов.
Метод единичной ячейки, рассмотренный в (7), применяется для анализа больших АР, состоящих из идентичных излучателей, возбуждаемых с одинаковой амплитудой и одинаковой разностью фаз между соседними элементами. Суть метода заключается в том, что все пространство АР делится две части: нижнюю, где помещается система питания, и верхнюю, в которую решетка излучает. В верхней части вокруг одного из излучателей образуют единичную ячейку, состоящую из двух электрических и двух магнитных стенок, простирающихся до бесконечности. Стенки располагают таким образом, чтобы выполнялись граничные условия и тем самым не нарушалась структура поля, сформированного под воздействием взаимного влияния элементов. После введения стенок можно пренебречь полем вне единичной ячейки, а саму ячейку можно рассматривать как своего рода волновод. Все взаимные связи между щелями учитываются автоматически. Такой подход позволяет использовать хорошо развитую теорию волноводов.
2. Расчет полевых и импедансных характеристик ФАР
Результаты, полученные на основе модели бесконечных периодических структур, позволяют оценить свойства центральных излучателей больших АР. Часто требуется выполнить расчеты для АР малых размеров, либо исследовать краевые эффекты в больших АР. Расчет взаимных сопротивлений можно выполнять и методами поэлементного подхода, но как правило это сложная электродинамическая задача. Решить данную задачу позволяет процедура, построенная на основе эквивалентности метода поэлементного расчета входных сопротивлений излучателя в бесконечной АР и метода, основанного на теории бесконечных периодических структур (2).
2.1 Входное сопротивление элемента бесконечной периодической линейной решетки
Для линейной решетки полосковых вибраторов, расположенных на многослойной диэлектрической подлжке (рис. 2.1) и имеющих распределение тока
![]() , (2.1)
, (2.1)
где ![]() -единичный вектор, входное сопротивление можно записать в виде (1)
-единичный вектор, входное сопротивление можно записать в виде (1)
![]() , (2.2)
, (2.2)
где J(y) – распределение тока по (2.1);
![]() - скалярная компонента функции Грина при разложении полей по волнам Е и Н.
- скалярная компонента функции Грина при разложении полей по волнам Е и Н.
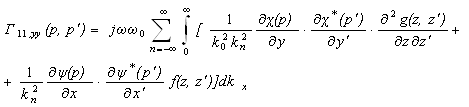 , (2.3)
, (2.3)
где ![]() - собственные функции (1);
- собственные функции (1);
![]() -характеристические части функции Грина.
-характеристические части функции Грина.
Записав выражения для характеристических частей и собственных функций и подставив их в (2.2) и (2.3), получим выражение для расчета входного сопротивления вибратора, имеющего структуру как на рис. 2.1 и находящегося в составе бесконечной решетки с периодом B (1)
где B=nA – период решетки;
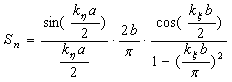 - множитель, учитывающий распределение тока по вибратору;
- множитель, учитывающий распределение тока по вибратору;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
α – угол наклона излучателей в решетке (α=0° – параллельные излучатели, α=90° – коллинеарные излучатели).
Для слоистой структуры, представленной на рис. 2.1, проводимость в сечении ![]() определяется по следующим рекурентным формулам:
определяется по следующим рекурентным формулам:
![]() ;
;
 ;
;
![]() ;
;
![]() ;
;
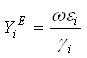 ;
;  ;
;
![]() ;
; ![]() ;
; ![]() .
.
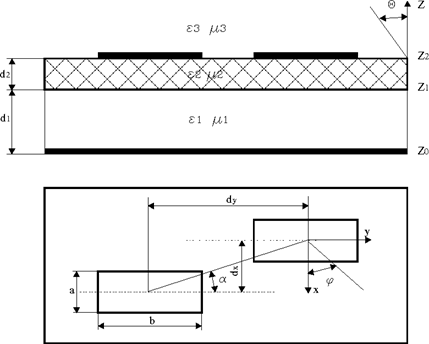
Рис. 2.1 Геометрия полосковых излучателей на многослойной диэлектрической подложке
Выражение для расчета входного сопротивления вибратора, имеющего структуру как на рис. 2.2и находящегося в составе бесконечной решетки с периодом B имеет следующий вид (1)
 , (2.5)
, (2.5)
Для слоистой структуры, представленной на рис. 2.2, проводимость в сечении ![]() определяется по следующим рекурентным формулам:
определяется по следующим рекурентным формулам:
![]() ;
;
![]() ;
;
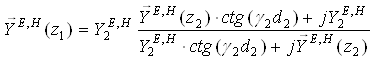 ;
;
![]() ;
;
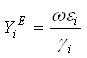 ;
;  ;
;
![]() ;
; ![]() ;
; ![]() .
.
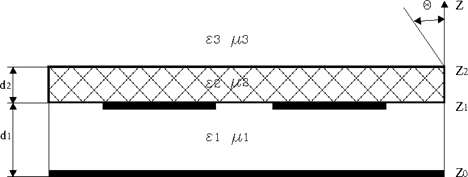
Рис. 2.2 Полосковые излучатели на перевернутой диэлектрической подложке
Разложение функции Грина по волнам Е и Н, используемые в данном случае, позволяет получить компактную и достаточно простую запись выражений для расчета входного сопротивления элемента, находящегося в составе бесконечной периодической линейной решетки.
2.2 Расчет взаимного сопротивления полосковых излучателей в составе бесконечной линейной решетки
При анализе антенных решеток конечных размеров необходимо знать взаимное сопротивление между излучателями. Одним из классических методов расчета взаимных сопротивлений является метод наводимых ЭДС. Для простых типов излучателей, размещенных на воздушной подложке, удается получить либо аналитические, либо легко рализуемые алгоритмы расчета для ЭВМ. Однако, в тех случаях, когда в излучающей структуре располагается слоистый диэлектрик, расчет взаимных сопротивлений между излучателями существенно усложняется, так как кроме пространственных волн на взаимную связь между излучателями оказывают влияние поверхностные волны, направляемы диэлектрическими слоями. Одним из решением проблемы является способ определения взаимных сопротивлений между излучателями, в котором используются результаты численных расчетов входного сопротивления излучателя в составе бесконечной линейной решетки (1, 2).
Рассмотрим бесконечную линейную решетку излучателей, период которой может принимать дискретные значения nA, где n=1,2,3… Входное сопротивление решетки с периодом nA при синфазном и равноамплитудном возбуждении определяется как
взаимное сопротивление между центральным и p – элементом решетки с периодом nA,
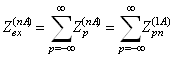 , (2.6)
, (2.6)
где ![]() - взаимные сопротивления между центральным и p‑м элементом (p
- взаимные сопротивления между центральным и p‑м элементом (p![]() 0) решетки с периодом nA, зависящее только от расстояния между излучателями;
0) решетки с периодом nA, зависящее только от расстояния между излучателями;
![]() - собственное сопротивление центрального излучателя.
- собственное сопротивление центрального излучателя.
В силу симметрии задачи (2.6) входное сопротивление можно записать в виде
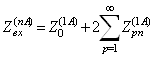 (2.7)
(2.7)
Для того, чтобы определить взаимное сопротивление между центральным излучателем и соседним, находящимся на расстоянии 1A, нужно из входного сопротивления АР с периодом 1А вычитать входное сопротивление АР с другими периодами, кратными 1А так, чтобы при этом компенсировались все взаимные сопротивления кроме одного, интересующего нас. Рассмотрим это более подробно на примерах.
Разность входных сопротивлений центральных элементов решеток с периодом 1А и 2А определяется как ![]() .
.
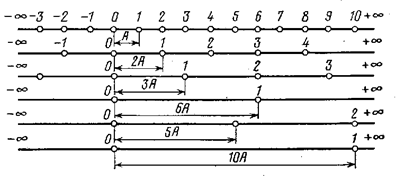
Рис. 2.3 Бесконечные линейные решетки с разными периодами
Так как ![]() (см. рис. 2.3), то эта разность входных сопротивлений равна сумме взаимных сопротивлений центального элемента решетки с периодом 1А со всеми нечетными элементами этой решетки. Далее рассмотрим бесконечные АР с периодом 3А и 6А. Если учесть, что
(см. рис. 2.3), то эта разность входных сопротивлений равна сумме взаимных сопротивлений центального элемента решетки с периодом 1А со всеми нечетными элементами этой решетки. Далее рассмотрим бесконечные АР с периодом 3А и 6А. Если учесть, что ![]() и
и ![]() , то разница между входными сопротивлениями центральных элементов данных решеток
, то разница между входными сопротивлениями центральных элементов данных решеток ![]() будет равна удвоенной сумме взаимных сопротивлений центрального элемента решетки с периодом 1А с элементами этой же решетки, имеющими номера 3 (2p‑1).
будет равна удвоенной сумме взаимных сопротивлений центрального элемента решетки с периодом 1А с элементами этой же решетки, имеющими номера 3 (2p‑1).
Если продолжить аналогичные рассуждения далее, то можно составить процедуру.
В первой сумме n=3,5,7….-простые, во второй сумме ![]() ,
,![]() -простые,
-простые,
Из предыдущих рассуждений ясно, что при вычислении ![]() из входного сопротивления решетки с периодом 1А исключаются собственное сопротивление центрального элемента и взаимные сопротивления между этим элементом и элементами данной решетки с четными номерами. При вычитании из
из входного сопротивления решетки с периодом 1А исключаются собственное сопротивление центрального элемента и взаимные сопротивления между этим элементом и элементами данной решетки с четными номерами. При вычитании из ![]() величины
величины ![]() из рассмотрения исключаются взаимные сопротивления между центральным элементом решетки с периодом 1А и элементами данной решетки с номерами 3 (2p‑1) (p=0, ±1, ±2, ±3.) и т.д.
из рассмотрения исключаются взаимные сопротивления между центральным элементом решетки с периодом 1А и элементами данной решетки с номерами 3 (2p‑1) (p=0, ±1, ±2, ±3.) и т.д.
Следовательно, при N→∞ величина ![]() соответствует значению взаимного сопротивления двух излучателей, разнесенных на расстояние 1A. При расчетах взаимного сопротивления между двумя излучателями с заданной точностью требуется конечное число итераций N в (2.8), которое определяется скоростью сходимости значений входного сопротивления
соответствует значению взаимного сопротивления двух излучателей, разнесенных на расстояние 1A. При расчетах взаимного сопротивления между двумя излучателями с заданной точностью требуется конечное число итераций N в (2.8), которое определяется скоростью сходимости значений входного сопротивления ![]() (n→∞) к значению собственного сопротивления излучателя. При использовании в (2.8) N итераций величина ошибки вычисления взаимного сопротивления будет определяться следующим выражением:
(n→∞) к значению собственного сопротивления излучателя. При использовании в (2.8) N итераций величина ошибки вычисления взаимного сопротивления будет определяться следующим выражением:
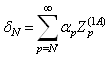 , (2.9)
, (2.9)
где ![]()
p – числовая последовательность, по которой осуществляется суммирование в процедуре (2.8);
![]() - следующее за Nчисло этой числовой последовательности.
- следующее за Nчисло этой числовой последовательности.
Для возбуждения пространственных волн выражение (2.9) можно записать в следующем виде:
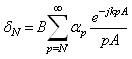 , (2.10)
, (2.10)
где k – волновое число;
B – коэффициент пропорциональности.
В случае возбуждения поверхностных волн выражение (2.9) можно записать в следующем виде:
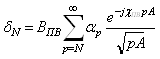 , (2.11)
, (2.11)
где ![]() - волновое число;
- волновое число;
![]() - коэффициент пропорциональности.
- коэффициент пропорциональности.
Ряд (2.10) является абсолютно сходящимся, ряд (2.11) сходится для всех А за исключением значений, кратных длине поверхностной волны.
Следует остановиться на оценке быстродействия данного алгоритма. Время счета одного значения взаимного сопротивления между излучателями складывается из времени счета 2·m значений входного сопротивления излучателя в составе бесконечной АР, где m – число слагаемых в процедуре (2.8).
2.3 Расчет взаимного сопротивления в двумерной плоской ФАР
Изложенный в предыдущем разделе метод определения взаимного сопротивления между излучателями в составе линейной антенной решетки может быть применен и для расчета двумерных плоских ФАР.
Рассмотрим ФАР, изображенную на рис.2.4. Ее можно представить в виде нескольких линейных антенных решеток. Например, излучатели с номерами 0; 0 1; 0 2; 0 3; 0 представляют линейную решетку из параллельных вибраторов (α=90°), а излучатели с номерами 0; 0 0; 1 0; 2 0; 3 – линейную решетку из коллинеарных вибраторов (α=0°), см. рис. 2.5. Для расчета взаимного сопротивления между 0; 0 и 1; 0 излучателем необходимо сначала по (2.4) при фиксированном значении α=90° вычислить несколько значений (N) входного сопротивления излучателя в составе бесконечной решетки, имеющей периоды, которые равны и кратны расстоянию между рассматриваемыми элементами ФАР. Затем согласно процедуре (2.8) следует определить взаимное сопротивление, исходя из полученных N значений входного сопротивления.
Поскольку антенная решетка является эквидистантной, то удобно проводить расчет входного сопротивления по (2.4) не между конкретными парами излучателей, а при фиксированном угловом направлении (например,![]() -см. рис. 2.5), в котором располагается выбранная линейная решетка из нескольких излучателей.
-см. рис. 2.5), в котором располагается выбранная линейная решетка из нескольких излучателей.
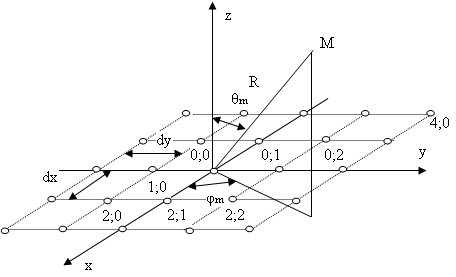
Рис. 2.4 Плоская ФАР
В этом случае создается массив расстояний, в котором исключаются повторяющиеся периоды, что сокращает число вычислений. Например, рассмотрим линейную решетку 0; 0 1; 0 2; 0 3; 0, расстояние между соседними излучателями составляет ![]() . Если рассматривать взаимное сопротивление отдельно между каждой парой излучателей (0; 0 и 0; 1; 0; 0 и 0; 2 и т.д.), то потребовалось бы составить следующие массивы расстояний для каждой пары:
. Если рассматривать взаимное сопротивление отдельно между каждой парой излучателей (0; 0 и 0; 1; 0; 0 и 0; 2 и т.д.), то потребовалось бы составить следующие массивы расстояний для каждой пары:
(![]() , 2
, 2![]() , 3
, 3![]() , 6
, 6![]() …) – массив расстояний для пары 0; 0 и 0; 1,
…) – массив расстояний для пары 0; 0 и 0; 1,
(2![]() , 4
, 4![]() , 6
, 6![]() , 12
, 12![]() …) – массив расстояний для пары 0; 0 и 0; 2,
…) – массив расстояний для пары 0; 0 и 0; 2,
(3![]() , 6
, 6![]() , 9
, 9![]() , 18
, 18![]() …) – массив расстояний для пары 0; 0 и 0; 3.
…) – массив расстояний для пары 0; 0 и 0; 3.
Если же рассматривать излучатели совместно, то потребуется один массив расстояний, в котором будут исключены повторяющиеся периоды:
(![]() , 2
, 2![]() , 3
, 3![]() , 4
, 4![]() ,6
,6![]() , 9
, 9![]() , 18
, 18![]() …) – массив расстояний при фиксированном угловом направлении.
…) – массив расстояний при фиксированном угловом направлении.
Так как излучатели одинаковые, то взаимное сопротивление между 0; 0 и 0; 1 будет равно взаимному сопротивлению между 0; 1 и 0; 2. Взаимное сопротивление между 0; 0 и 0; 2 будет равно взаимному сопротивлению между 0; 1 и 0; 3. Таким образом, при расчете взаимного сопротивления между излучателями ФАР достаточно рассчитать взаимное сопротивление между 0; 0 излучателем и всеми остальными. Взаимное сопротивление между другими парами будет выбираться из ранее рассчитанных значений из условия совпадения угла и расстояния между излучателями.
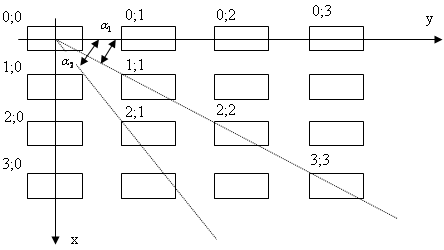
Рис. 2.5 Представление двумерной решетки в виде нескольких линейных решеток
Сделанные выше замечания позволяют создать алгоритм расчета взаимных сопртивлений между излучателями в составе плоской ФАР достаточно универсальным и значительно снижающим вычислительные затраты машинного времени по сравнению с решением задачи напрямую.
2.4 Расчет входного сопротивления излучателя с учетом взаимных связей
Входное сопротивление излучателя в составе антенной решетки и находящегося изолированно от других не равнозначны. Это объясняется наличием взаимной связи между излучателями в составе решетки. При сближении элементов взаимная связь возрастает и уменьшается ток каждого отдельного элемента синфазной антенной решетки при неизменной подводимой к излучателю мощности.
Систему входов АР размера ![]() описывает следующая матрица сопротивлений
описывает следующая матрица сопротивлений
 , (2.12)
, (2.12)
где ![]() - собственные сопротивления излучателей;
- собственные сопротивления излучателей;
![]() - взаимное сопротивление между i и j излучателями.
- взаимное сопротивление между i и j излучателями.
Амплитудное распределение можно представить в виде матрицы-столбца комплексных напряжений
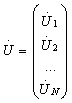 (2.13)
(2.13)
Токи на излучателях можно представить в виде матрицы-столбца комплексных токов
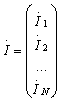 (2.14)
(2.14)
Тогда матрица сопротивлений (Z)однозначно связывает матрицу напряжений (U) и матрицу токов (I), согласно (3)
 (2.15)
(2.15)
Амплитудное распределение в АР задается заранее, матрицу взаимных сопротивлений (Z) можно вычислить, используя методику, описанную в предыдущих разделах работы, тогда матрицу токов (I) на элементах с учетом взаимных связей можно определить через следующее выражение, записанное в матричной форме
где матрица ![]() имеет смысл матрицы проводимости. В этом случае, входное сопротивление для каждого элемента антенной решетки с учетом взаимных связей можно записать в виде (3)
имеет смысл матрицы проводимости. В этом случае, входное сопротивление для каждого элемента антенной решетки с учетом взаимных связей можно записать в виде (3)
где =1…N;
N – общее число излучателей в ФАР.
Например, для ФАР из четырех элементов входное сопротивление первого элемента будет иметь вид
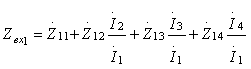 .
.
2.5 Определение полевых характеристик ФАР
В плоской двумерной ФАР, имеющей направление ориентации главного максимума диаграммы направленности ![]() и
и ![]() (рис. 2.4) дискрет фазы между излучателями по оси ОХ и ОY можно представить в следующем виде
(рис. 2.4) дискрет фазы между излучателями по оси ОХ и ОY можно представить в следующем виде
![]()
![]() , (2.18)
, (2.18)
где k – волновое число;
![]() ,
, ![]() - шаг решетки по оси ОХ и ОY соответственно.
- шаг решетки по оси ОХ и ОY соответственно.
В этом случае фаза на излучателях будет определяться выражением (3)
![]() , (2.19)
, (2.19)
где =1..m и q=1..– координаты излучателя по оси ОХ и ОY соответственно;
![]() ;
;![]() - координаты центрального излучателя.
- координаты центрального излучателя.
Разность хода лучей от центра излучения решетки и конкретного излучателя до точки наблюдения с угловыми параметрами θ и φ составит
В силу линейности уравнений Максвелла электромагнитное поле антенной решетки представляет собой сумму полей отдельных элементов. Если эти элемениы имеют равные размеры, характеризуются одним и тем же законом распределения излучающих токов и ориентированы в пространстве одинаковым образом, то электромагнитное поле в дальней зоне может быть представлено в виде произведения векторной диаграммы направленности одиночного элемента на множитель направленности АР (3)
![]() , (2.21)
, (2.21)
где ![]() - амплитудный множитель, зависящий от общей мощности когерентных генераторов, питающих систему излучателей;
- амплитудный множитель, зависящий от общей мощности когерентных генераторов, питающих систему излучателей;
![]() - векторная диаграмма направленности одиночного элемента;
- векторная диаграмма направленности одиночного элемента;
![]() - множитель направленности АР.
- множитель направленности АР.
В главной системе координат ![]() отдельных излучателей различаются на величину
отдельных излучателей различаются на величину ![]() (2.20). Учитывая, что комплексные амплитуды возбуждения отдельных излучателей могут быть различными, получим следующее представление суммарной диаграммы направленности (3)
(2.20). Учитывая, что комплексные амплитуды возбуждения отдельных излучателей могут быть различными, получим следующее представление суммарной диаграммы направленности (3)
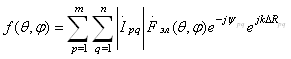 (2.22)
(2.22)
Сравнивая выражение (2.21) и (2.22) можно заметить, что множитель направленности АР имеет вид
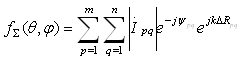 , (2.23)
, (2.23)
где и q– координаты излучателя по оси ОХ и ОY соответственно;
![]() - общее число излучателей в ФАР;
- общее число излучателей в ФАР;
![]() - разность хода лучей;
- разность хода лучей;
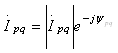 - комплексная амплитуда тока возбуждения на (q) излучателе.
- комплексная амплитуда тока возбуждения на (q) излучателе.
Таким образом, если задано амплитудное распределение, линейные размеры антенной решетки, то определив ![]() по (2.19) и
по (2.19) и ![]() по (2.20) и приняв амплитуду тока
по (2.20) и приняв амплитуду тока ![]() , равной амплитуде напряжения возбуждения, можно найти множитель направленности АР без учета взаимной связи. Для учета взаимной связи вместо расчета фазы возбуждения необходимо рассчитать по (2.16) комплексную амплитуду тока
, равной амплитуде напряжения возбуждения, можно найти множитель направленности АР без учета взаимной связи. Для учета взаимной связи вместо расчета фазы возбуждения необходимо рассчитать по (2.16) комплексную амплитуду тока ![]() и использовать эти значения в (2.23). Тип одиночного излучателя и его геометрия определяют его диаграмму направленности
и использовать эти значения в (2.23). Тип одиночного излучателя и его геометрия определяют его диаграмму направленности ![]() , что позволяет, в конечном счете, рассчитать общую диаграмму направленности ФАР
, что позволяет, в конечном счете, рассчитать общую диаграмму направленности ФАР
3. Программы для расчета характеристик ФАР
3.1 Общие сведения
В результате дипломной работы был создан пакет программ, предназначенный для расчета полевых и импедансных характеристик плоской ФАР, излучатели в составе которой представляют собой полосковые вибраторы или резонаторные излучатели, выполненные на многослойном диэлектрике (см. рис.2.1 и рис.2.2). Для каждого типа диэлектрика разработан собственный пакет. Эти пакеты идентичны, имеют одинаковые алгоритмы расчета и интерфейс, поэтому в дальнейшем будем рассматривать только один из пакетов.
Программный пакет выполнен в рамках математического пакета для инженерных расчетов Mathcad 2001, который благодаря наглядной форме отображения расчетных соотношений и результатов доступен для понимания пользователями. Кроме того, формулы, выходные данные, графики, построенные в данном пакете, могут быть легко импортированы в современные текстовые редакторы, такие как Word, что удобно при создании научных статей, отчетов и других работ.
Пакет, структурная схема пакета приведена на рис. 3.1, включает четыре программы, каждая из которых выполняет определенные функции:
· ФАР_вз_связь.mcd – центральная программа пакета и выполняет расчет определение полевых и импедансных характеристик ФАР с учетом и без учета взаимной связи между излучателями;
· вз_сопрот.mcd– вспомогательная программа пакета и предназначена для исследования зависимости взаимного сопротивления излучателей от расстояния между ними;
· рез_размер.mcd – программа, вычисляющая входное сопротивление излучателя при различной его длине и ширине. Эта программа может быть полезна при определении резонансного размера излучателя bрез;
· ФАР_полоса.mcd – программа выполняющая расчет полевых и импедансных характерисик ФАР в полосе частот по результатам, полученным в программе ФАР_вз_связь.mcd. Эти результаты записаны в файлах данных.
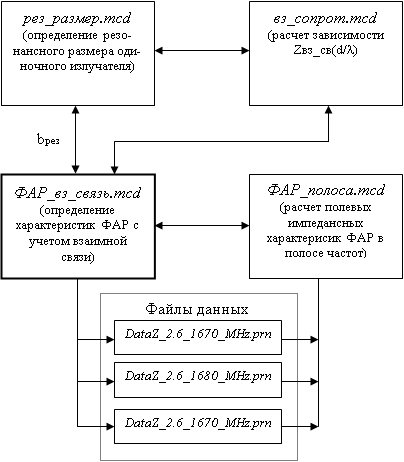
Рис. 3.1 Структурная схема пакета программ
Программы связаны между собой с помощью гиперссылок, изображенные на рис.3.1 в виде стрелок, что позволяет удобно переходить от одной программы к другой не выходя из среды общей Mathcad. Это создает цельность структуры и общность восприятия пакета.
3.2 Программа для расчета полевых и импедансных характеристик ФАР
3.2.1 Описание применения
Программа, имеющая название ФАР_вз_связь.mcdявляется центральной программой разработанного пакета и выполняет расчет характеристик плоской ФАР, выполненной из полосковых вибраторов или резонансных излучателей на многослойном диэлектрической подложке, с учетом и без учета взаимной связи между излучателями. Выходными данными программы являются:
· входное сопротивление одиночного излучателя;
· входное сопротивление каждого илучателя ФАР с учетом взаимной связи, рассчитанное по (2.17);
· входное сопротивление ФАР и КСВ при последовательной схеме питания;
· входное сопротивление ФАР и КСВ при двоично-этажной схеме питания;
· матрица взаимных сопротивлений (2.12);
· диаграмма направленности ФАР с учетом и без учета взаимной связи, рассчитаная по (2.24).
Входные данные задаются пользователем вручную в тексте программы, состав входных данных представлен в разделе 3.2.4.
3.2.2 Методика испытаний
Объектом испытаний является файл с именем ФАР_вз_связь.mcd, который является программой для расчета полевых и импедансных характеристик ФА
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Разработка передатчика для радиовещания в синхронной сети
Министерство Российской Федерации по связи и информатизацииКафедра РПУКурсовой проектпо курсу Радиопередающие устройства"Разработка
- Разработка печатного модуля РЭС с использованием учебных алгоритмов САПР
- Разработка печатного узла шестиуровневого индикатора напряжения аккумулятора
- Разработка прибора присутствия
- Разработка приёмника радиолокационной станции обнаружения
- Разработка программного обеспечения для голосового управления трехмерными моделями функционирования промышленных роботов
- Разработка программы определительных испытаний
Испытанием – это экспериментальное определение количественных и качественных характеристик свойств объекта как результата воздейст
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.


 , (
, (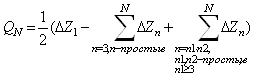 (
(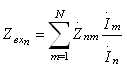 , (
, (