Скачать

Разработка программного обеспечения для голосового управления трехмерными моделями функционирования промышленных роботов

Распознавание человеческой речи является одной из сложных научно-технических задач. В настоящее время пользователями вычислительных машин и средств, оснащенных вычислительными машинами, становятся люди, не являющиеся специалистами в области программирования. Проблема речевого управления возникла, кроме того, в связи с тем, что в некоторых областях применения речь стала единственно возможным средством общения с техникой (в условиях перегрузок, темноты или резкого изменения освещенности, при занятости рук, чрезвычайной сосредоточенности внимания на объекте, который не позволяет отвлечься ни на секунду, и т.д.). Хотя в этой области и достигнуты существенные успехи, тем не менее, системы распознавания еще весьма далеки по своим возможностям от человеческих.

Проблема реализации речевого диалога человека и технических средств - актуальная задача современной кибернетики.

Задача машинного распознавания речи привлекает внимание специалистов уже очень давно. Тем не менее, продвинуться далеко в этом направлении пока не удалось. Чисто формально процесс распознавания речи можно описать буквально в нескольких фразах. Аналоговый сигнал, генерируемый микрофоном, оцифровывается, и далее в речи выделяются так называемые фонемы, то есть элементарные фрагменты, из которых состоят все произносимые слова. Затем определяется, какое слово, какому сочетанию фонем соответствует, и строится соответствующий словарь. Распознать слово - значит найти его в этом словаре по произнесенному сочетанию фонем. По мере развития компьютерных систем становится все более очевидным, что использование этих систем намного расширится, если станет возможным использование человеческой речи при работе непосредственно с компьютером, и в частности станет возможным управление машиной обычным голосом в реальном времени, а также ввод и вывод информации в виде обычной человеческой речи.

В настоящее время всё более актуальным становится управление роботом при помощи голосовых команд. Однако создание программного обеспечения для голосового управления промышленным роботом предусматривает проведение экспериментов во время разработки программы на всех этапах разработки. Проведение таких экспериментов, обеспечивающих устранение недостатков, ошибок программы, является экономически невыгодным в условиях промышленного производства и приводит к повышению стоимости разработки и отладки программного обеспечения. Для уменьшения затрат на создание программного обеспечения целесообразно разработать программу, которая обеспечит трёхмерное моделирование голосового управления промышленным роботом, что приводит к необходимости проведения экспериментов в условиях производства лишь на последнем этапе разработки программного обеспечения.

Темой данного исследования является голосовое управление трёхмерными моделями функционирования промышленных роботов. Его задачами является анализ методов цифровой обработки звуковых сигналов, анализ систем распознавания речи, разработка программного обеспечения для распознавания команд управления промышленным роботом.

1. Цифровая обработка сигналов и её использование в системах распознавания речи

1.1 Дискретные сигналы и методы их преобразования

Акустическое колебание, формируемое в речевом тракте человека, является непрерывно изменяющимся процессом. С математической точки зрения его можно описать функцией непрерывного времени 1. Аналоговые (непрерывные во времени) сигналы будут обозначаться через х_а(1). Речевой сигнал можно представить и последовательностью чисел. Последовательности обозначаются через х(п). Если последовательность чисел представляет собой последовательность мгновенных значений, аналогового сигнала, взятых периодически с интервалом Т, то эта операция дискретизации обозначается через х_а(пТ). На рис. 1.1 показан пример речевого сигнала в аналоговой форме и в виде последовательности отсчетов, взятых с частотой дискретизации 8 кГц.

Рис. 1.1 – Представление речевого сигнала

Для удобства даже при рассмотрении дискретных сигналов иногда на графике будет изображается непрерывная функция, которая может рассматриваться как огибающая последовательности отсчетов. При изучении систем цифровой обработки речи требуется несколько специальных последовательностей. Единичный отсчет или последовательность, состоящая из одного единичного импульса, определяется как

 (1.1)

Последовательность единичного скачка имеет вид

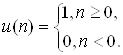
 (1.2)

Экспоненциальная последовательность

 (1.3)

Если а - комплексное число, т. е. , то

 (1.4)

Если z=1 и , х() - комплексная синусоида; если . х() -действительное; если z<1 и , то х() - экспоненциально-затухающая осциллирующая последовательность. Последовательности этого типа часто используются при представлении линейных систем и моделировании речевых сигналов.

Обработка сигналов включает преобразование их в форму, удобную для дальнейшего использования. Таким образом, предметом интерес представляют дискретные системы или, что то же самое, преобразования входной последовательности в выходную. Подобные преобразования далее изображаются на структурных схемах. Многие системы анализа речевых сигналов разработаны для оценивания переменных во времени параметров по последовательности мгновенных значений речевого колебания. Подобные системы имеют многомерный выход, т. е. одномерная последовательность на входе, представляющая собой речевой сигнал, преобразуется в векторную последовательность на выходе.

При обработке речевых сигналов особенно широкое применение находят системы, инвариантные к временному сдвигу. Такие системы полностью описываются откликом на единичный импульс, Сигнал на выходе системы может быть рассчитан по сигналу на входе и отклику на единичный импульс h() с помощью дискретной свертки

 (1.5a)

где символ * обозначает свертку. Эквивалентное выражение имеет вид

 (1.5б)

Линейные системы, инвариантные к временному сдвигу, применяются при фильтрации сигнала и, что более важно, они полезны как модели речеобразования.

Анализ сигналов и расчет систем значительно облегчаются при их описании в частотной области. В этой связи полезно кратко остановиться на представлении сигналов и систем в дискретном времени с использованием преобразования Фурье и z-преобразования (1).

1.1.1 Прямое и обратное г-преобразование

Прямое и обратное г-преобразование последовательности определяется двумя уравнениями:

 (1.6a)

  (1.6б)

Прямое z-преобразование х() определяется уравнением (1.6а). В общем случае Х(z) - бесконечный ряд по степеням z^-1; последовательность х() играет роль коэффициентов ряда. В общем случае подобные степенные ряды сходятся к конечному пределу только для некоторых значений z. Достаточное условие сходимости имеет вид

  (1.7)

Множество значений, для которых ряды сходятся, образует область на комплексной плоскости, известную как область сходимости. В общем случае эта область имеет вид (2)

  (1.8)

1.1.2 Преобразование Фурье

Описание сигнала в дискретном времени с помощью преобразование Фурье задаётся в виде

 (1.9a)

 (1.9б)

Эти уравнения представляют собой частный случай уравнений (1.6а,б).

Преобразование Фурье получается путём вычисления z -преобразования на единичной окружности, т. е. подстановкой . Частота  может быть интерпретирована как угол на z - плоскости. Достаточное условие существования преобразования Фурье можно получить, подставляя в (1.7)

 (1.10)

Важная особенность преобразования Фурье последовательности состоит в том, что оно является периодической функцией со с периодом 2к. С другой стороны, поскольку  представляет собой значение Х(z) на единичной окружности, оно должно повторяться после каждого полного обхода этой окружности, т. е. когда со изменится на  рад (1).

1.1.3 Дискретное преобразование Фурье

Как и в случае аналоговых сигналов, если последовательность периодическая с периодом N, т. е.

 (1.11)

то х() можно представить в виде суммы синусоид, а не в виде интеграла. Преобразование Фурье для периодической последовательности имеет вид

 (1.12а)

 (1.12б)

Это точное представление периодической последовательности. Однако, основное преимущество данного описания заключается в возможности несколько иной интерпретации уравнений (1.12). Рассмотрим последовательность конечной длины х(), равную нулю вне интервала B этом случае z-преобразование имеет вид

 (1.13)

Если записать X(z) в N равноотстоящих точках единичной окружности, т. е. , k= 0, 1,…,N-1, то получим

 (1.14)

Если при этом построить периодическую последовательность в виде бесконечного числа повторений сегмента х(),

 (1.15)

то отсчеты (), как это видно из (1.12а) и (1.14), будут представлять собой коэффициенты Фурье периодической последовательности х() в (1.15). Таким образом, последовательность длиной N можно точно описать с помощью дискретного преобразования Фурье (ДПФ) в виде

 (1.16)

 (1.17)

Следует иметь в виду, что все последовательности при использовании ДПФ ведут себя так, как если бы они были периодическими функциями, т. е. ДПФ является на самом деле представлением периодической функции времени, заданной (1.15). Несколько иной подход при использовании ДПФ заключается в том, что индексы последовательности интерпретируются по модулю N. Это следует из того факта, что если х() имеет длину N, то

Введение двойных обозначений позволяет отразить периодичность, присущую представлению с помощью ДПФ. Эта периодичность существенно отражается на свойствах ДПФ. Очевидно, что задержка последовательности должна рассматриваться по модулю N. Это приводит, например, к некоторым особенностям выполнения дискретной свертки.

Дискретное преобразование Фурье со всеми его особенностями является важным способом описания сигналов по следующим причинам: 1) ДПФ можно рассматривать как дискретизированный вариант z -преобразования (или преобразования Фурье) последовательности конечной длительности; 2) ДПФ очень сходно по своим свойствам (с учетом периодичности) с преобразованием Фурье и z-преобразованием; 3) N значений Х(k) можно вычислить с использованием эффективного (время вычисления пропорционально NlogN) семейства алгоритмов, известных под названием быстрых преобразований Фурье (БПФ).

Дискретное преобразование Фурье широко используется при вычислении корреляционных функций, спектров и при реализации цифровых фильтров, а также часто используется и при обработке речевых сигналов (1-5).

1.1.4 Спектральный анализ

Спектральный анализ – это метод обработки сигналов, который позволяет выявить частотный состав сигнала. Поскольку анализируемые сигналы во многих случаях имеют случайный характер, то важную роль в спектральном анализе играют методы математической статистики. Частотный состав сигналов определяют путем вычисления оценок спектральной плотности мощности (СПМ). Задачами вычисления СПМ являются обнаружение гармонических составляющих в анализируемом сигнале и оценивание их параметров. Для решения указанных задач требуется соответственно высокая разрешающая способность по частоте и высокая статистическая точность оценивания параметров. Эти два требования противоречивы. Аргументы в пользу выбора высокого разрешения или высокой точности оценки СПМ зависят от того, что интересует исследователя: устойчивые оценки в пределах всего диапазона частот или высокая степень обнаруживаемости периодических составляющих.

Все методы цифрового спектрального анализа можно разделить, на две группы (6-7): классические методы, базирующиеся на использовании преобразований Фурье, и методы параметрического моделирования, в которых выбирается некоторая линейная модель формирующего фильтра и оцениваются его параметры. К первой группе относят корреляционный и периодограммные методы. Ко второй группе относят методы оценивания СПМ на основе авторегрессии скользящего среднего и др.

Периодограммный метод обеспечивает вычисление оценки СПМ непосредственно по числовой последовательности х(nТ₀), формируемой путем дискретизации стационарного эргодического случайного процесса x(t). Периодограммная оценка СПМ равна (6-7)

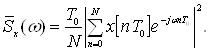 (1.18)

Выражение (1.18) соответствует возможности вычисления СПМ с помощью преобразования Фурье непосредственно по реализации исходного сигнала.

Вычисленная с помощью (1.18) оценка СПМ является несостоятельной, т.е. с увеличением N она не улучшается. Для получения состоятельной оценки ее необходимо сглаживать. Кроме этого, при выполнении преобразования Фурье последовательности х(nТ₀) конечной длины /V происходит «размывание» спектра, которое также оказывает влияние на состоятельность оценки СПМ.

Ограничение последовательности х(nТ₀) конечным числом значений равносильно умножению исходной бесконечной последовательности х₀ (nТ₀) на другую последовательность

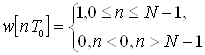
 (1.19)

которую называют прямоугольным окном. Тогда можно записать

 (1.20)

Преобразование Фурье последовательности х(nТ₀) равно свертке преобразований Фурье последовательности х₀ (nТ₀) и прямоугольного окна w(nТ₀)

 (1.21)

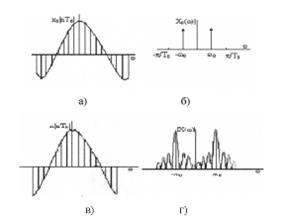
Рисунок 1.2 – Размывание спектра: (а – исходная бесконечная последовательность; б – модуль преобразования Фурье от х₀ (nТ₀); в - последовательность х₀ (nТ₀), умноженная на прямоугольное окно; г - модуль преобразования Фурье последовательности х(nТ₀))

При выборе оконных функций используются следующие параметры: ширина основного лепестка, максимальный уровень боковых лепестков, скорость спадания уровня боковых лепестков (6,7,10).

Здесь ширина основного лепестка определена на уровне 3 дБ ниже его максимума и измерена в единицах разрешения преобразования Фурье, т.е. 2π/N, где N - длина окна.

Для повышения состоятельности оценки (1.18) выполняют её сглаживание. Имеется несколько методов сглаживания: Даньелла, Бартлетта, Уэлча (6,7).

Метод Даньелла основан на осреднении значений СПМ в пределах смежных спектральных частот.

В соответствии с методом Бартлетта состоятельность оценки СПМ повышают усреднением оценок СПМ коротких реализаций, полученных из

одной реализации длиной N отсчетов. Пусть дана реализация длиной N отсчетов. Она разбивается на n_s неперекрывающихся сегментов, длиной N_s=N/s отсчетов. Для каждого сегмента по формуле (1.18) вычисляется выборочная оценка СПМ. Сглаженная оценка СПМ получается путем усреднения по всем , сегментам

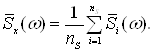 (1.30)

Если последовательность х() представляет нормальный стационарный эргодический процесс, то сглаженная оценка имеет дисперсию обратно пропорциональную числу сегментов .

Спектральное разрешение оценки задается приближенным равенством

 (1.31)

В методе Уэлча подход Бартлетта применяется к перекрывающимся сигментам исходной последовательности х(), и каждый сегмент взвешивается с помощью оконной функции для уменьшения смещения оценок из-за эффекта «просачивания» энергии в боковые лепестки. Цель перекрытия сегментов - увеличить число усредняемых участков при фиксированной длине последовательности и тем самым повысить точность оценок СПМ. Метод Уэлча - один из самых распространенных периодограммных методов (6,7).

Обозначим через  величину сдвига между сегментами, которая должна удовлетворять условию , где - максимальное имя корреляции анализируемого процесса. При выполнении этого условия получим =int((N-N_s)/+l)слабо коррелированных сегментов. Отсчеты каждого сегмента взвешиваются окном w()

 (1.32)

Выборочное значение СПМ сегмента р оценивается по формуле

 (1.33)

где

 (1.34)

 (1.35)

Сглаженная оценка периодограммы Уэлча вычисляется по формуле

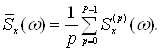 (1.36)

Введение перекрытия сегментов в методе Уэлча позволяет уменьшить изменчивость оценки СПМ, Так же как и в методе Бартлетта, дисперсия оценки СПМ по методу Уэлча обратно пропорциональна числу сегментов, но благодаря большему числу сегментов, значение дисперсии будет меньше.

1.2 Основы цифровой фильтрации

Цифровой фильтр представляет собой систему с постоянными параметрами (инвариантную к сдвигу), работающую в дискретном времени. Напомним, что для таких систем сигнал на входе и выходе связан дискретной сверткой (1.5). Соответствующее соотношение между z-преобразованиями имеет вид

  (1.37)

Прямое z-преобразование отклика на единичный импульс H(z) называется передаточной функцией системы. Преобразование Фурье отклика на единичный импульс называется частотной характеристикой. Обычно  представляет собой комплексную функцию со, которую можно записать в виде

  (1.38)

или через модуль и фазу

  (1.39)

Инвариантная к сдвигу линейная система называется физически реализуемой, если h()=0 при <0. Линейная система устойчива, если для любой ограниченной по уровню входной последовательности выходная последовательность также ограничена. Необходимым и достаточным условием устойчивости линейной системы с постоянными параметрами является

  (1.40)

Это условие аналогично (1.10) и оказывается достаточным для существования .

Сигналы на входе и выходе линейных инвариантных к сдвигу систем, таких, например, как фильтры, связаны дискретной сверткой (1.5) и кроме того, разностным уравнением

 (1.41)

Вычисляя z-преобразование от обеих частей, можно получить

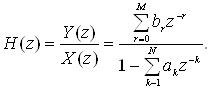 (1.42)

Сравнивая (1.41) и (1.42), полезно отметить следующее. Если задано разностное уравнение вида (1.41), то H(z) можно получить непосредственной подстановкой коэффициентов при входном сигнале в числитель передаточной функции к соответствующим степеням z^-1, а коэффициенты при выходном сигнале - в знаменатель к соответствующим степеням z^-1.

Передаточная функция в общем случае является дробно рациональной. Таким образом, она определяется положением нулей и полюсов на z-плоскости. Это означает, что H(z) можно представить в виде

 (1.43)

При рассмотрении z-преобразования отмечалось, что физически реализуемые системы имеют область сходимости вида |z|>R₁. Если система, кроме того, еще и устойчива, то R₁ должно быть меньше единицы, таким образом единичная окружность входит в область сходимости. Иначе говоря, для устойчивой системы все полюсы H(z) должны лежать внутри единичной окружности.

Достаточно определить два типа линейных систем с постоянными параметрами. Это системы с конечной импульсной характеристикой (КИХ) и системы с бесконечной импульсной характеристикой (БИХ). Эти два класса обладают отличными друг от друга свойствами, которые будут рассмотрены ниже.

Если все коэффициенты а_k. в уравнении (1.22) равны нулю, то разностное уравнение принимает вид

 (1.44)

Сравнивая (1.44) с (1.56), можно отметить, что

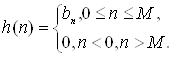 (1.45)

Системы с КИХ обладают рядом важных свойств. Передаточная функция H(z) таких систем представляет собой полином по степеням z^-1 и, таким образом, не имеет ненулевых полюсов, а содержит только нули. Системы с КИХ могут обладать строго линейной фазо-частотной характеристикой (ФЧХ). Если h() удовлетворяет условию

 (1.46)

то

 (1.47)

где  - действительная или чисто мнимая величина в зависимости от знака в (1.48).

Возможность получения строго линейной ФЧХ является очень важным обстоятельством применительно к речевым сигналам в тех случаях, когда требуется сохранить взаимное расположение элементов сигнала. Это свойство систем с КИХ существенно облегчает решение задачи их проектирования, поскольку все внимание можно уделять лишь аппроксимации амплитудно-частотной характеристики (АЧХ). За это достоинство фильтра с линейной ФЧХ, приходится расплачиваться необходимостью аппроксимации протяженной импульсной реакции в случае фильтров с крутыми АЧХ. Хорошо разработаны три метода проектирования КИХ-фильтров с линейными ФЧХ: взвешивания, частотной выборки и проектирования оптимальных фильтров с минимаксной ошибкой (1-3). Второй и третий методы являются оптимизационными и используют итеративный (в отличие от замкнутой формы) подход для определения коэффициентов фильтра. Несмотря на простоту метода взвешивания, широкое применение нашли все три метода. Это обусловлено завершенностью глубоких исследований оптимальных КИХ-фильтров а, кроме того, наличием подробно описанных программ, позволяющих пользователю легко рассчитать любой фильтр (1,2,11).

При рассмотрении вопросов реализации цифровых фильтров полезно изображать их в виде схем. Разностное уравнение (1.25) изображено на рис. 1.4. Подобные схемы, называемые структурными, описывают в графической форме те операции, которые необходимо проделать над входной последовательностью для получения сигнала на выходе.

Для фильтра после подстановки (1.49) в(1.51) и выполнения интегрирования получается

 (1.52)

Импульсная характеристика (1.32) определена при любых целых значениях к и является бесконечной, поэтому ограничивают значения k. Пусть |k|≤К, где К=(N-1)/2 для фильтров с нечётными значениями N и К=N/2 для фильтров с чётными значениями N. Тогда конечная импульсная характеристика, соответствующая (1.52), записывается в виде

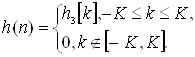 (1.53)

Импульсная характеристика (1.53) является некаузальной, так как имеет ненулевые значения при k<0. Чтоб получить каузальную характеристику, необходимо задержать  на К тактов, т.е.

 (1.54)

Синтезированный таким образом фильтр будет иметь значительные пульсации вблизи частоты среза. Указанные пульсации представляют эффект Гиббса, проявляющийся вблизи точек разрыва заданной частотной характеристики. Эффект Гиббса обусловлен ограничением длительности бесконечной импульсной характеристики .

Конечная импульсная характеристика , получаемая из , может быть также представлена в виде

 (1.55)

где w(k) - прямоугольное весовое окно длиной N отсчётов. Умножение заданной импульсной характеристики на прямоугольное окно приводит к искажению частотной характеристики синтезируемого фильтра. Частотная характеристика, соответствующая (1.55), будет равна свёртке заданной частотной характеристики прямоугольного окна. Таким образом, эффект Гиббса связан с пульсирующим поведением частотной характеристики прямоугольного весового окна.

Для уменьшения отрицательного влияния эффекта Гиббса применяют весовые окна, отличные от прямоугольного. Здесь имеет место аналогия со спектральным анализом, когда для уменьшения утечки энергии в боковые лепестки применяют оконные функции. С целью обеспечения линейности фильтра низких частот указанные оконные функции должны быть симметричными w(k)=w(N-k-1) и определены для значений k, лежащих диапазоне 0≤k≤N-1 (6).

1.3 Особенности акустической фонетики и её учёт при обработке речевых сигналов

1.3.1 Механизм речеобразования

Речь состоит из последовательности звуков. Звуки и переходы между ними служат символическим представлением информации. Порядок следования звуков (символов) определяется правилами языка. Изучение этих правил и их роли в общении между людьми составляет предмет лингвистики, анализ и классификация самих звуков речи — предмет фонетики. При обработке речевых сигналов с целью повышения их информативного содержания либо для выделения содержащейся в сигнале информации полезно располагать как можно большим количеством сведений о структуре сигнала, например, о способе кодирования информации в сигнале (1).

Голосовой тракт начинается с прохода между голосовыми связками,называемого голосовой щелью, и заканчивается у губ. Голосовой тракт, таким образом, состоит из гортани (от пищевода до рта) и рта, или ротовой полости. У взрослого мужчины общая длина голосового тракта составляет примерно 17 см. Площадь поперечного сечения голосового тракта, которая определяется положением языка, губ, челюстей и небной занавески, может изменяться от нуля (тракт полностью перекрыт) до примерно 29 см². Носовая полость начинается у нёбной занавески и заканчивается ноздрями. При опущенной небной занавеске носовая полость акустически соединена с голосовым трактом и участвует в образовании носовых звуков речи. На рис. 1.4 показано подробное схематическое изображение речеобразующей системы. Для полноты в диаграмму включены и такие органы, как легкие, бронхи и трахея, расположенные ниже гортани. Совокупность этих органов и служит источником энергии для образования речи. Речь представляет собой акустическую волну, которая вначале излучается этой системой при выталкивании воздуха из легких и затем преобразуется в голосовом тракте. Основные особенности колебания легко объяснить на основе подробного анализа механизма образования речи. Звуки речи могут быть разделены на три четко выраженные группы по типу возбуждения. Вокализованные звуки образуются проталкиванием воздуха через голосовую щель, при котором периодически напрягаются и расслабляются голосовые связки и возникает квазипериодическая последовательность импульсов потока воздуха, возбуждающая голосовой, тракт.

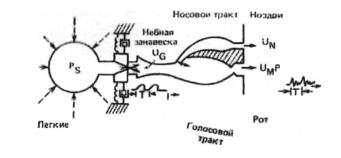
Рисунок 1.4 – Схема речеобразующих органов человека (1,13)

Фрикативные или невокализованные звуки генерируются при сужении голосового тракта в каком-либо месте (обычно в конце рта) и проталкивании воздуха через суженное место со скоростью, достаточно высокой для образования турбулентного воздушного потока. Таким образом, формируется источник широкополосного шума, возбуждающего голосовой тракт.

При произнесении взрывных звуков голосовой тракт полностью закрывается (обычно в начале голосового тракта). За этой смычкой возникает повышенное сжатие воздуха. Затем воздух внезапно высвобождается. Область малого уровня соответствует периоду полного закрытия голосового тракта. Голосовой тракт и носовая полость показаны на рис. 1.4 в виде труб с переменной по продольной оси площадью поперечного сечения. При прохождении звуковых волн через эти трубы их частотный спектр изменяется в соответствии с частотной избирательностью трубы. Этот эффект похож на резонансные явления, происходящие в трубах органов и духовых музыкальных инструментов. При описании речеобразования резонансные частоты трубы голосового тракта называют формантными частотами или просто формантами. Формантные частоты зависят от конфигурации и размеров голосового тракта: произвольная форма тракта может быть описана набором формантных частот. Различные звуки образуются путем изменения формы голосового тракта. Таким образом, спектральные свойства речевого сигнала изменяются во времени в соответствии с изменением формы голосового тракта.

Переменные во времени спектральные характеристики речевого сигнала с помощью звукового спектрографа могут быть высвечены в виде графика. Этот прибор позволяет получить двумерный график, называемый спектрограммой, на которой по вертикальной оси отложена частота, а по горизонтальной – время. Плотность зачернения графика пропорциональна энергии сигнала. Таким образом, резонансные частоты голосового тракта имеют вид затемненных областей на спектрограмме. Вокализованным областям сигнала соответствует появление четко выраженной периодичности временной зависимости, в то время как невокализованные интервалы выглядят почти сплошными (1).

1.3.2 Акустическая фонетика

Многие языки, в том числе и английский, можно описать набором отдельных звуков или фонем. Изучать фонему можно по-разному. Лингвисты, например, изучают отличительные характеристики фонем (1,2). Четыре широких класса звуков образуют гласные, дифтонги, полугласные и согласные. Каждый из классов разбит на подклассы по способу и месту образования звука в голосовом тракте. Каждая фонема может быть отнесена к классу протяжных или кратковременных звуков. Протяжные звуки образуются при фиксированной (инвариантной ко времени) форме голосового тракта, который возбуждается соответствующим источником. К этому классу относятся гласные, фрикативные (вокализованные и невокализованные) носовые согласные. Остальные звуки (дифтонги, полугласные, аффрикаты и взрывные согласные) произносятся при изменяющейся форме голосового тракта. Они образуют класс кратковременных звуков.

Гласные. Гласные образуются при квазипериодическом возбуждении голосового тракта неизменной формы импульсами воздуха, возникающими вследствие колебания голосовых связок. Как будет показано ниже, зависимость площади поперечного сечения голосового тракта от координаты (расстояния) вдоль его продольной оси определяет резонансные частоты тракта (форманты) и характер произносимого звука. Эта зависимость называется функцией площади поперечного сечения. Функция площади поперечного сечения для каждой гласной зависит в первую очередь от положения языка; вместе с тем на характер звука оказывают влияние положения челюстей, губ и, в меньшей степени, небной занавески. Например, при произнесении звука |а|, голосовой тракт открыт в начале, а в его конце тело языка образует сужение. Наоборот, при произнесении звука |и|, язык образует сужение в начале голосового тракта и оставляет его открытым в конце. Таким образом, каждому гласному звуку может быть поставлена в соответствие форма голосового тракта (функция площади поперечного сечения), характерная для его произношения. Очевидно, что это соответствие неоднозначное, так как у разных дикторов голосовые тракты различны; Другим представлением гласного звука является его описание с помощью набора резонансных частот голосового тракта. Это описание также зависит от диктора. Петерсон и Барней (1) провели измерения формантных (резонансных) частот с помощью звукового спектрографа для гласных, произнесенных различными дикторами.

На спектрограммах четко выделяются различные резонансные области, характерные для каждой гласной. Акустические колебания, иллюстрируя периодичность вокализованных звуков, позволяют также путем анализа одного периода выявить грубые спектральные характеристики. Например, акустическое колебание звука |и| состоит из низкочастотного затухающего колебания, на которое накладывается относительно высокочастотная составляющая. Это соответствует низкой частоте первой форманты и высоким частотам второй и третьей формант. Два резонанса, расположенных на близких частотах, расширяют спектр колебания. Наоборот, в акустическом колебании гласной |у| энергия высокочастотных составляющих относительно мала, что соответствует низким частотам первой и второй формант. Подобный анализ может быть проведен для всех гласных.

Дифтонги. Дифтонгом называется участок речи, соответствующий одному слогу, который начинается с одной гласной и затем постепенно переходит в другую. На основе этого определения можно выделить следующие дифтонги: |эй|, |оу|, |ау|, |ой|, |ай|.

Дифтонги образуются путём плавного изменения формы голосового тракта.

Полугласные. Группу звуков, содержащих |в|, |й| описать довольно трудно. Эти звуки называются полугласными, гак как по своим свойствам они напоминают гласные звуки. Обычно их характеризуют плавным изменением функции площади поперечного сечения голосового тракта между смежными фонемами. Таким образом, акустические характеристики этих звуков существенно зависят от произносимого текста. Удобно рассматривать эти звуки как переходные, сходные с гласными. Их структура близка к структуре гласных и дифтонгов.

Носовые звуки (соно