Скачать

Разработка и исследование способа обнаружения аномальных значений

Содержание

Основная часть

Выводы

Библиографический список

аномальное аппаратура оборудование радиосигнал

При регистрации, обработке и обмене данными в современных измерительно-вычислительных и информационных системах потоки сигналов искажены действием помех (шумов), природа возникновения которых различна и зачастую носит случайный характер. Шумовая составляющая может содержать и аномальные значения. Для решения задачи выделения полезной составляющей нестационарного случайного процесса применяются различные классические процедуры фильтрации, результаты которых зависят от наличия в исследуемом процессе аномальных значений.

Аномальными называют значения, резко отличающиеся по величине и статистическим свойствам на фоне основной группы значений реализации процесса. Природа возникновения и источники аномальных значений различны, это может быть импульсная помеха, кратковременные повышения уровня шумов на входах приемников, сбой в работе регистрирующей аппаратуры, отказ оборудования, кратковременное внешнее воздействие на измерительный элемент, «залипание» разряда цифрового счетчика, атмосферные воздействия при передаче радиосигналов, индустриальные помехи и т.д.

До недавнего времени на практике для обнаружения аномальных значений широко применялись ручные способы, основанные на визуальном просмотре зарегистрированных реализаций нестационарных случайных процессов и сравнение их с контрольными реализациями известной формы. Помимо субъективизма в критериях обнаружения аномальных значений, основанных, главным образом, на опыте и интуиции экспериментатора, подобные способы не допускают автоматизации процедур обработки исследуемых реализаций.

Для преодоления отмеченных недостатков, как показано в работах (1, 2), предлагается использовать теорию статистических решений, которая позволяет формализовать алгоритмы проверок и выбрать критерий обнаружения аномальных значений. Возможно применение как параметри-ческих, так и непараметрических методов теории решения. В первом случае необходимо располагать априорными сведениями как о функции полезной составляющей, так и о законе распределения шумовой составляющей, а также и о его параметрах (математическом ожидании, дисперсии, корреляционной функции). Использование непараметрических методов обработки требует значительно меньше априорной информации, но их эффективность определяется параметрами обработки, которые, в свою очередь, зависят от функции полезной и закона распределения шумовой составляющих процесса.

В связи с этим значительный интерес представляет разработка и исследование способа обнаружения аномальных значений при анализе нестационарных случайных процессов, представленных единственной реализацией.

В работах (3, 4) представлен метод выделения полезной составляющей нестационарного случайного процесса, который имеет высокую эффективность в условиях  априорной неопределенности. Суть метода состоит в размножении не самой реализации исходного процесса, а оценок, получаемых определенным образом. Автор работ (3, 4), основываясь на основных принципах метода размножения оценок, предлагает и метод обнаружения аномальных значений при анализе нестационарных случайных процессов. В работах (3, 4, 5, 6 и др.) аналитически определены значения основных параметров метода обнаружения аномальных значений и показана его эффективность при анализе как стационарных, так и нестационарных случайных процессов с аддитивной шумовой составляющей.

К одному из достоинств метода обнаружения аномальных значений можно отнести также следующее: применение двухпорогового критерия принятия решения об аномальности значения процесса позволяет получить результаты,  при которых с увеличением величины аномальных значений, выборочные значения вероятности ошибки первого рода  стремятся к минимальным значениям, в то время как выборочные значения вероятности правильного обнаружения  стремятся к максимальным значениям (4, 5, 6).

Наряду с достоинствами предлагаемого метода обнаружения аномальных значений, представленного в работах (4, 5), выявлено, что он обладает весьма существенными недостатками, одним из которых является зависимость порогового значения от некоторого постоянного коэффициента . Правильный выбор коэффициента  позволит повысить эффективность обнаружения аномальных значений.

Поэтому в данной работе на основе проведенных исследований предлагается модификация уже существующего метода обнаружения аномальных значений, которая заключается в выборе правила определения коэффициента  при задании порогового значения.

Модификация предлагаемого в работе способа обнаружения аномальных значений предполагает введение адаптации порогового значения относительно коэффициента  при априорно фиксированном значении вероятности ошибки первого рода .

Предлагаемый в данной работе способ предполагает наличие единственной дискретной реализации исследуемого нестационарного случайного процесса . Априорная информация об исследуемом процессе заключается в том, что на некоторых интервалах времени полезная составляющая процесса является гладкой функцией (6), т.е. достаточно точно описывается полиномом не выше второй степени:

.                                         (1)

Реализация исследуемого процесса разбивается на интервалы случайной длины, получаемые следующим образом: с помощью генератора случайных чисел, равномерно распределенных в интервале (0;1), получают  чисел . Используя выражение , осуществляется взаимнооднозначное отображение промежутка (0;1) на интервале значений исследуемого нестационарного случайного процесса , получая при этом соответствующее разбиение числами  промежутка  на  непересекающихся интервалов, где

 , .                      (2)

Вводятся обозначения для интервалов разбиения:

,  , …,   .(3)

Каждый интервал разбиения  содержит не менее  отсчетов (минимальная длина интервала разбиения) исходного нестационарного случайного процесса из набора , в противном случае случайные числа, формирующие данный интервал разбиения , отбрасываются и генерируются заново. Наличие этого условия означает, что .

Для получения каждой новой оценки процедура разбиения отрезка  на  интервалов случайной длины (с проверкой выше указанного условия) повторяется. В результате получаем  разбиений временного отрезка  (7) .

   …  

   …   .                                     (4)

   …  

На каждом интервале разбиения , где  и , с помощью метода наименьших квадратов находятся оценки , ,  коэффициентов аппроксимирующего полинома  как решение системы линейных уравнений:

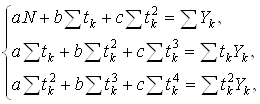            (5)

где символ означает суммирование по всем -м значения, которые принадлежат интервалу разбиения  и , .

Результатом действия способа будет набор определенных на отрезке  сглаживающих функций , где , каждая из которых является «кусочно-квадратичной»:

(6)

где ,  и .

Определяются значения разности  между исходным нестационарным случайным процессом   и оценкой сглаживающих функций :

, .(7)

При оценке параметров разностного процесса  на каждом интервале разбиения  используется один из методов робастного оценивания (8), т.е. оценка параметров  математического ожидания  и среднеквадратического отклонения  производится по -усеченной выборке. Для этого на каждом интервале разбиения  получаем ряд ранжированных значений и  оценку математического ожидания  и среднеквадратического отклонения , которая проводится без учета первого и последнего значения ранжированного ряда. Тогда выражения для оценок математического ожидания  и среднеквадратического отклонения  принимают следующий вид (9):

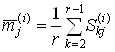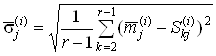 и  ,(8)

где   .Далее на каждом интервале разбиения исследуемого нестационарного случайного процесса устанавливается  пороговое значение

,       (9)

где  – некоторый коэффициент,  и . Превышение значений разностного процесса  на каждом интервале разбиения установленного порогового значения (9) штрафуется, т.е. если выполняется условие:

,                              (10)

то  получает одно штрафное значение. В соответствии с методом размножения оценок (4) вышеизложенная процедура определения штрафов повторяется р раз и для каждого повторения проверяется условие (10) для каждого значения , где ; ;;  – объем выборки исследуемого нестационарного случайного процесса;  – количество интервалов разбиения; – количество повторений процедур (2)–(10).

Таким образом, происходит накопление ряда штрафных значений для элементов исходной реализации исследуемого процесса, т.е.:

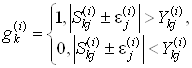,      (11)

где – ряд штрафных значений  и ,.

По окончанию обработки для всех оштрафованных значений исходной реализации определяется суммарное значение штрафов 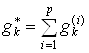 и максимальное значение ряда . Далее проверяется условие:  если

,  (12)

то k-е значение из входной реализации нестационарного случайного процесса  будет трактоваться как аномальное. Условие (12) получено на основе проведения имитационного моделирования при различных моделях полезной и шумовой составляющих нестационарного случайного процесса.

Для случая обнаружения аномальных значений в реализации нестационарного случайного процесса выбирать значение коэффициента  только по оценкам среднеквадратического отклонения шумовой составляющей процесса является нецелесообразным, так как наличие аномальных значений существенно влияет на погрешность оценки полезной составляющей процесса и, как следствие, на оценку среднеквадратического отклонения разностного процесса. Следует также отметить, что на каждом интервале разбиения значение коэффициента  не может быть фиксированным.

В связи с этим предлагается ввести адаптацию порогового значения о назначении штрафов (9) по коэффициенту  относительно априорно фиксированного значения вероятности ошибки первого рода. С этой целью  проведены исследования зависимости  коэффициента  от объема выборки , от значения среднеквадратического отклонения случайного процесса  для различных стационарных процессов при априорно фиксированных значениях вероятности ошибки первого рода .

В результате получены зависимости выборочных значений коэффициента  от объема исследуемой выборки и среднеквадратического отклонения шумовой составляющей процесса, то есть . Входная реализация представляет собой стационарный центрированный гауссовский случайный процесс. Исследования проводились на выборках объемом = 5, 7, 9, 11, 13 и 15 значений и среднеквадратическом отклонении случайного процесса = 0,1–0,5. В результате  проведенных исследований были получены зависимости выборочных значений коэффициента  при различных априорно фиксированных значениях вероятности ошибки первого рода . Усреднение значений  коэффициента  производилось по 1 000 выборок (10, 11, 12).

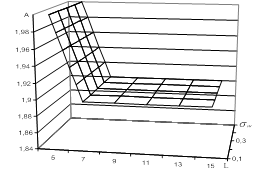
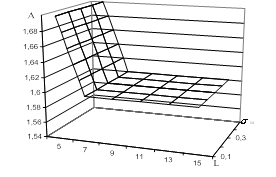
На рис. 1 приведены графики зависимости выборочных значений коэффициента  для объема выборки  и  среднеквадратического отклонения случайного процесса  при априорно фиксированных значениях вероятности ошибки первого рода  (при =0,05 – рис. 1а, при =0,1 – рис. 1б).

а)                                                                     б)

Рис. 1. Зависимость  для гауссовского закона плотности распределения вероятности случайного процесса: а – при ; б – при

Из анализа полученных зависимостей, представленных на рис. 1, следует, что при различных фиксированных значениях вероятности ошибки первого рода  с увеличением объема выборки  выборочные значения коэффициента  стремится к некоторому постоянному значению и практически не зависит от значения среднеквадратического отклонения случайного процесса. Выборочные значения коэффициента  для  выборок  возрастают в среднем на 5 %.

Также приведены результаты  исследований зависимости коэффициента  от объема выборки  и среднеквадратического отклонения , когда стационарный случайный процесс представлен равномерным и рэлеевским законами распределения. Результаты полученных зависимостей представлены на рис. 2а – для равномерного и на рис. 2б – для рэлеевского законов плотности распределения вероятности случайного процесса, при априорно фиксированном значении ошибки первого рода =0,05.

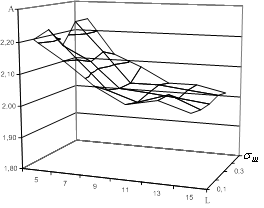
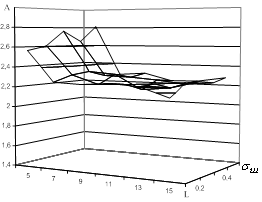
а)                                                                 б)

Рис. 2. Зависимость  при  :

а – для равномерного закона;

б – для рэлеевского законов плотности распределения вероятности случайных процессов

Из анализа графиков, представленных на рис. 2а и б, видно, что выборочные значения коэффициента  практически не зависят от среднеквадратического отклонения стационарного случайного процесса  и незначительно зависит от объема исследуемой выборки .

Таким образом, проведенные исследования показывают, что выборочные значения коэффициента  для рассмотренных законов распределения случайных процессов практически не зависят от объема исследуемой выборки  и среднеквадратического отклонения стационарного случайного процесса , а зависят только от априорно задаваемого значения вероятности ошибки первого рода  (10, 11, 12). В связи с этим исследуются зависимости выборочных значений коэффициента  от априорно фиксированного значения вероятности ошибки первого рода , т.е. , для различных законов плотности распределения вероятности стационарных случайных процессов (гауссовского, равномерного, рэлеевского) при значении . Результаты, которые представлены на рис. 3, получены при ,  и .

На рис. 3 приведены зависимости значения оценок коэффициента  от вероятности ошибки первого рода : график 1 – рэлеевский; график 2 – равномерный и график 3 – гауссовский законы плотности распределения вероятности стационарного случайного процесса.

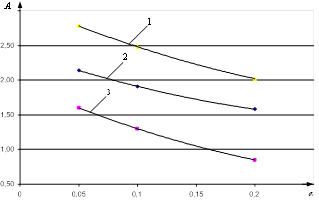
Рис. 3. Зависимость  для различных законов распределения случайных процессов

Из анализа графиков, представленных на рис. 3, следует, что выборочные значения коэффициента  для всех представленных законов распределения стационарного случайного процесса существенно зависят от априорно задаваемых значений вероятности ошибки первого рода .

На рис. 4 представлен усредненный график зависимости   для исследуемых стационарных случайных процессов.

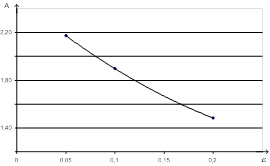
Рис. 4. Усредненная зависимость  для рассмотренных стационарных случайных процессов

Графическая зависимость, представленная на рис. 4, может быть аппроксимирована полиномом второй степени вида (6, 7):

.                           (13)

Полученные результаты исследования зависимости коэффициента   позволяют при адаптации порогового значения (9) вместо постоянного значения коэффициента  использовать его значение, которое вычисляется в соответствии с (13). Использование уравнения (13) в оценке порогового значения (9) позволяет использовать предложенный способ обнаружения аномальных значений при фиксированном значении вероятности ошибки первого рода .

Для исследования эффективности способа обнаружения аномальных значений с адаптацией порогового значения проводится сравнительный  анализ предлагаемого способа и способа обнаружения аномальных значений без адаптации порогового значения.

Критерием эффективности предлагаемого в данной работе способа обнаружения аномальных значений в реализации нестационарного случайного процесса выступают выборочные значения вероятности правильного обнаружения  и вероятности ошибки первого рода . Вероятность ошибки первого рода  (вероятность ложной тревоги) определяет вероятность принятия значения процесса за аномальное значение. Вероятность правильного обнаружения  определяет вероятность правильного решения о наличии аномального значения в исходной реализации нестационарного случайного процесса. Использование вышесказанного критерия для оценки эффективности предлагаемых  в работе способа осуществляются по усредненным значениям, т.е. в качестве выборочных значений вероятности правильного обнаружения , и вероятности ошибки первого рода  рассмотрены их средние значения, полученные по множеству реализаций (порядка 1 000).

В данной работе исследуются модели нестационарных процессов, которые представляют собой единственную реализацию дискретного процесса , полученного в равноотстоящие моменты времени , где  и , т.е. модели вида (3):

,                                          (14)

,                                           (15)

где ,, ,  – полезная, аддитивная, мультипликативная шумовая и аномальная составляющие входного процесса соответственно, где , – объем выборки исследуемого процесса.

Исследование для нестационарных случайных процессов проводятся, когда полезная составляющая процесса  представлена простыми моделями функций: гармонической, экспоненциальй, полиномиальными, а также составной и сложной моделями. Составная модель функции исследуемого процесса состоит из  параболы, синусоиды, константы и экспоненты – модель огибающая радиоимпульса на выходе резонансного усилителя при расстройке относительно резонансной частоты. Модель сложной функции представляет собой сумму некоторой константы и синусоиды.

Шумовая составляющая процесса представлена гауссовским, равномерным  и рэлееевским законами плотности распределения вероятности.   В качестве аномальной составляющей процесса рассматривались одиночные аномального значения  с различной  величиной  и местом расположения в выборке исследуемого нестационарного случайного процесса.

На основе имитационного моделирования в работах (3, 4) при анализе нестационарных случайных процессов получены зависимости выборочных значений вероятности ошибки первого рода  и вероятности правильного обнаружения  для способа обнаружения аномальных значений без адаптации, т.е. когда значение коэффициента  в пороговом значении (9) задается фиксированным , и с адаптацией порогового значения (9), т.е. когда значение коэффициента  определяется выражением  (13) (4).

Исследования эффективности предлагаемого способа проводятся для случая, когда модель нестационарного случайного процесса является аддитивной (14). Аддитивная  шумовая составляющая процесса  имеет гауссовский закон плотности распределения вероятности. Одиночные аномальные значения распределены равномерно по всей реализации нестационарного случайного процесса  и составляют 5 % от выборки N. Исследования проводятся для различных значений величины аномальных значений , т.е.: ,,,,,  – среднеквадратическое отклонение аддитивной шумовой составляющей. Значения вероятности ошибки первого рода для способа с адаптацией порогового значения априорно фиксируется .

В результате проведенных исследований для нестационарных случайных  процессов получены зависимости выборочных значений вероятности правильного обнаружения . Для случая, когда не используется адаптация порогового значения, – графики  , , , ,  и с применением  адаптация порогового значения – графики 1, 2, 3, 4, 5 (рис. 5).

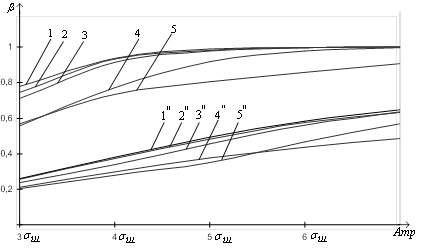
Рис. 5. Зависимость выборочных значений вероятности правильного обнаружения   для способа без адаптации и способа с адаптацией порогового значения при

Зависимости  на рис. 5 представлены  для различных моделей функций полезной составляющей : графики 1,  – экспоненциальной; графики 2,  – параболической; графики 3,  – гармонической; графики 4,  – составной и графики 5,  –  сложной функции.

Анализ результатов, представленных на рис. 5, показывает, что при введении адаптации порогового значения выборочные значения вероятности правильного обнаружения  возрастают для всех рассмотренных функций полезной составляющей . Причем для параболической, гармонической и экспоненциальной модели функций, при величине аномальных значений порядка , выборочные значения вероятности правильного обнаружения  возрастают примерно на 66 %. С увеличением величины аномальных значений () выборочные значения вероятности правильного обнаружения  увеличиваются примерно на 54 %. Из анализа зависимостей  также следует, что при использовании адаптации порогового значения, с увеличением величины аномальных значений , вероятность правильного обнаружения  асимптотически стремится к единице независимо от модели функции полезной составляющей  (4, 5).

Применяя адаптацию порогового значения, также получены зависимости выборочных значений вероятности ошибки первого рода , которые представлены на рис. 6.

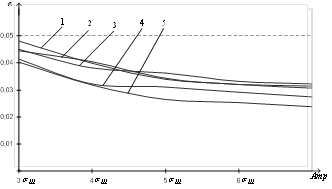
Рис. 6. Зависимость выборочных значений ошибки первого рода  для способа с адаптацией порогового значения  при

Зависимости  на рис. 6  представлены  для следующих моделей функций полезной составляющей сигнала : график 1 – параболической; график 2  –  составной; график 3 – экспоненциальной; график 4 – гармонической; график 5 –  сложной.

Из анализа полученных зависимостей  следует, что при использовании адаптации порогового значения выборочные значения вероятности ошибки первого рода  практически не превосходят априорно задаваемого значения, т.е. , для всех исследуемых нестационарных случайных процессов (рис. 6).

В данной работе также исследуется эффективность адаптивного способа обнаружения аномальных значений  в зависимости от места расположения аномальных значений в выборке нестационарного случайного процесса.

Рассматривается модель с аддитивной шумовой составляющей , закон плотности распределения вероятности которой является центрированным гауссовским случайным процессом со среднеквадратическим отклонением . В качестве модели функции полезной составляющей  используются следующие нормированные функции: экспоненциальная, гармоническая, составная.

Аномальные значения с фиксированной величиной  составляют 5 % от объема исследуемой выборки . Рассматриваются случаи, когда аномальные значения располагаются в начале выборки, в середине выборки, в конце выборки и равномерно по всей выборке нестационарного случайного процесса  , где .

В результате проведенных исследований получены выборочные значения вероятности правильного обнаружения  для случая без адаптации и с адаптацией порогового значения, которые представлены в табл. 1.

Таблица 1

Выборочные значения вероятности правильного обнаружения