Прогнозирование урожайности различными методами
Содержание
1. Задание
2. Аналитическое выравнивание
3. Метод экспоненциального сглаживания
4. Метод скользящих средних
5. Выравнивание при помощи рядов Фурье
Выводы
1. Задание
По имеющимся исходным данным урожайности озимой пшеницы в Волгоградский области провести расчеты прогнозных значений на последующие шесть лет для выявления закономерных или случайных изменений.
Исходные данные урожайности:
| 1947 | 1948 | 1949 | 1950 | 1951 | 1952 | 1953 | 1954 | 1955 | 1956 | 1957 | 1958 |
| 3,5 | 5,2 | 2,2 | 3,6 | 7,1 | 6,9 | 4,1 | 5,3 | 10,1 | 4,8 | 7,7 | 16,8 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1959 | 1960 | 1961 | 1962 | 1963 | 1964 | 1965 | 1966 | 1967 | 1968 | 1969 |
| 9,8 | 14,5 | 13,7 | 19,0 | 5,0 | 12,0 | 11,3 | 17,5 | 13,1 | 17,9 | 9,6 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
2. Аналитическое выравнивание
Выберем в качестве функций регрессии – линейную, параболическую, гиперболическую и показательную:
![]()
![]() .
.
Гиперболическую и показательную можно линеаризовать и применить МНК к этим функциям как к линейным. Для гиперболической функции введем новую переменную:
![]() .
.
Тогда получим:
![]() ,
,
где
![]() .
.
Для показательной функции проведем следующие преобразования. Прологарифмируем обе части уравнения: ![]() . Сделаем замены:
. Сделаем замены:
![]() ,
, ![]() ,
, ![]() .
.
Получим:
![]() ,
,
откуда найдем: ![]() ,
, ![]() ,
, ![]() .
.
Применим ПО MS Excel 2003 и Stata 7.0. Посчитаем коэффициент корреляции:

Коэффициент корреляции значим.
Построим линейную регрессию
| Регрессионная статистика | ||||||
| Множественный R | 0,717687 | |||||
| R-квадрат | 0,515074 | |||||
| Нормированный R-квадрат | 0,491982 | |||||
| Стандартная ошибка | 3,693991 | |||||
| Наблюдения | 23 | |||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 1 | 304,3725 | 304,3725 | 22,30559 | 0,000116 | |
| Остаток | 21 | 286,557 | 13,64557 | |||
| Итого | 22 | 590,9296 | ||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 3,014625 | 1,592152 | 1,893427 | 0,072162 | -0,29644 | 6,325686 |
| Переменная X 1 | 0,548419 | 0,11612 | 4,722879 | 0,000116 | 0,306935 | 0,789903 |
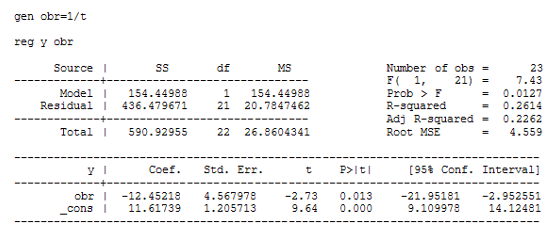
Регрессия для гиперболической функции:
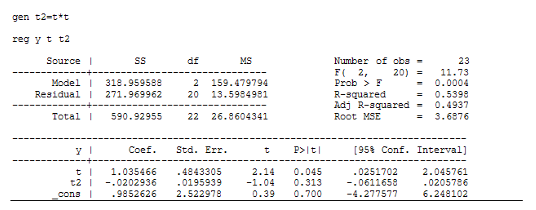
Регрессия для параболической функции:
Регрессия для показательной функции:
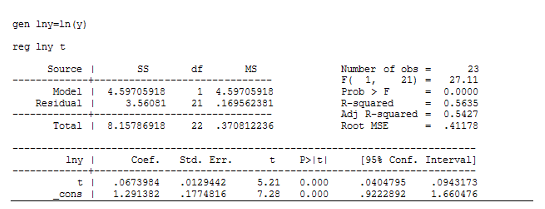
Как видно из этих данных, коэффициент детерминации у регрессии для гиперболической функции значительно хуже, чем у других моделей. А константа и коэффициент при переменной ![]() в модели параболической регрессии не значимы согласно t-критерию Стьюдента.
в модели параболической регрессии не значимы согласно t-критерию Стьюдента.
Коэффициенты детерминации для моделей линейной и показательной регрессий примерно одиноковы, причем R-квадрат больше у показательной регрессии. Сравним эти 2 модели по другим показателям. Рассчитаем среднюю квадратическую ошибку уравнения тренда и информационные критерии Акейка и Шварца:
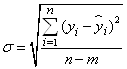 ,
, ![]() ,
, ![]()
Чем меньше значение информационных критериев, тем лучше модель.
Итак, для модели линейной регрессии получим:
AIC=5,131843277
BIC=2,658769213 σ=3,694
Для модели регрессии показательной функции имеем:
AIC= 5,477785725 BIC= 2,831740437 σ=4,028
Все 3 показателя лучше в первом случае.
Применим модель линейной регрессии для аналитического выравнивания исходного ряда. Модель такова:
у=3,01+0,55t;
Значения уровней ряда, полученных по модели, и остатков представлены в следующей таблице:
| Наблюдение | Предсказанное Y | Остатки |
| 1 | 3,563043478 | -0,063043478 |
| 2 | 4,111462451 | 1,088537549 |
| 3 | 4,659881423 | -2,459881423 |
| 4 | 5,208300395 | -1,608300395 |
| 5 | 5,756719368 | 1,343280632 |
| 6 | 6,30513834 | 0,59486166 |
| 7 | 6,853557312 | -2,753557312 |
| 8 | 7,401976285 | -2,101976285 |
| 9 | 7,950395257 | 2,149604743 |
| 10 | 8,498814229 | -3,698814229 |
| 11 | 9,047233202 | -1,347233202 |
| 12 | 9,595652174 | 7,204347826 |
| 13 | 10,14407115 | -0,344071146 |
| 14 | 10,69249012 | 3,807509881 |
| 15 | 11,24090909 | 2,459090909 |
| 16 | 11,78932806 | 7,210671937 |
| 17 | 12,33774704 | -7,337747036 |
| 18 | 12,88616601 | -0,886166008 |
| 19 | 13,43458498 | -2,13458498 |
| 20 | 13,98300395 | 3,516996047 |
| 21 | 14,53142292 | -1,431422925 |
| 22 | 15,0798419 | 2,820158103 |
| 23 | 15,62826087 | -6,02826087 |
Спрогнозируем урожайность озимой пшеницы на последующие 6 лет
| Прогнозные значения | |
| t | y |
| 24 | 16,17667984 |
| 25 | 16,72509881 |
| 26 | 17,27351779 |
| 27 | 17,82193676 |
| 28 | 18,37035573 |
| 29 | 18,9187747 |
Из графика видно, что урожайность с каждым последующим годом будет возрастать и достигнет через шесть лет значения практически в 2 раза большего, чем в 1969 году. Этот результат достигнут в результате существенного роста урожайности зерновых культур.
Проверим наличие автокорреляции в данном динамическом ряду. Для этого составим следующие таблицы:
Расчет коэффициента автокорреляции 1-го порядка
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

