Скачать

Приложения определенного интеграла к решению некоторых задач механики и физики

1. Моменты и центры масс плоских кривых. Если дуга кривой задана уравнением y=f(x), a≤x≤b, и имеет плотность ¹) =(x), то статические моменты этой дуги M_x и M_y относительно координатных осей Ox и Oy равны

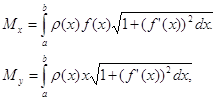
моменты инерции I_Х и I_у относительно тех же осей Ох и Оу вычисляются по формулам

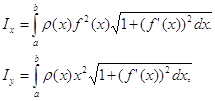
а координаты центра масс  и  — по формулам

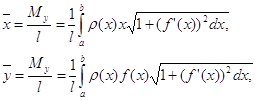
где l— масса дуги, т. е.

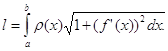
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох

и Оу дуги цепной линии y=chx при 0≤x≤1.

¹) Всюду в задачах, где плотность не указана, предполагается, что кривая однородна и =1.

Имеем: Следовательно,

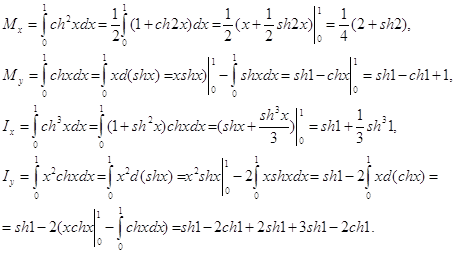
Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти.

Имеем:

Отсюда получаем:

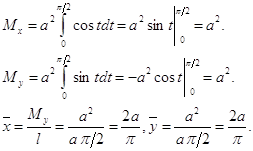
В приложениях часто оказывается полезной следующая

Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.

 Пример 3. Найти координаты центра масс полуокружности

Вследствие симметрии . При вращении полуокружности вокруг оси Ох получается сфера, площадь поверхности которой равна , а длина полуокружности равна па. По теореме Гульдена имеем

Отсюда , т.е. центр масс C имеет координаты C.

2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах 4—7.

Пример 4. Скорость прямолинейного движения тела выражается формулой  (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.

Так как путь, пройденный телом со скоростью (t) за отрезок времени (t₁,t₂), выражается интегралом

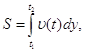
то имеем:

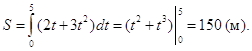
Для подготовки данной работы были использованы материалы с сайта http://www.monax.ru/