Скачать

Полупроводниковый преобразователь тепловой энергии окружающей среды

Анатолий Зерний

Проблема современной энергетики состоит в том, что производство электроэнергии – источник материальных благ человека находится в губительном противостоянии с его средой обитания – природой и как результат этого – неизбежность экологической катастрофы.

Поиск и открытие альтернативных экологически чистых способов получения электроэнергии – актуальнейшая задача человечества.

Одним из источников энергии, является природная окружающая среда: воздух атмосферы, воды морей и океанов, которые содержат огромное количество тепловой энергии, получаемой от Солнца.

Рассмотрим для примера изолированный кристалл собственного полупроводника, который легирован (см. рис.1) донорной примесью вдоль оси X по экспоненциальному закону

N_д(x) = f (e^kx).

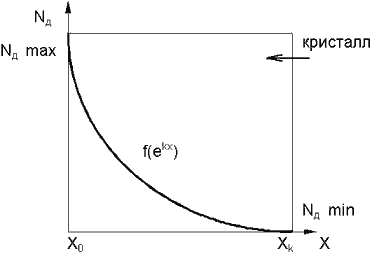
Рис. 1. Кристалл полупроводника легированый донорной примесью

Левая часть кристалла (X₀) легируется до такой концентрации N_дмакс, чтобы уровень Ферми находился у дна зоны проводимости полупроводника, а правая часть кристалла (X_к) легируется до минимально возможной концентрации N_дмин, чтобы уровень Ферми находился посредине запрещенной зоны полупроводника, при заданной температуре.

Основными носителями заряда, в данном случае, являются электроны (n).

Для простоты рассуждений, неосновными носителями – дырками (р) пренебрегаем из-за малой их концентрации.

В некоторый условный начальный момент, когда закон распределения концентрации электронов совпадает с законом распределения донорной примеси (n=N_д), кристалл в целом является электрически нейтральным и в каждом его элементарном объеме выполняется условие np=n_i², а вдоль оси X существует положительный градиент концентрации (см. рис.2) основных носителей – электронов dn/dx>0.

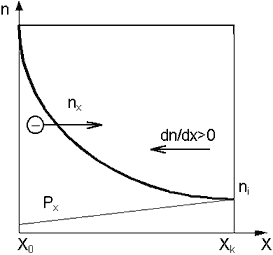
Рис. 2. Закон распределения концентрации основных носителей в кристалле

Под действием сил теплового движения и в результате наличия градиента концентрации, электроны начинают диффундировать в кристалле вдоль оси X из области высокой их концентрации (X₀) в область низкой концентрации (X_к), в результате – электронейтральность кристалла нарушается.

Электроны, движущиеся слева направо, оставляют после себя положительно заряженные ионы донорной примеси N_д⁺.

Эти ионы, жестко связанные с кристаллической решеткой полупроводника, образуют в левой части кристалла неподвижный положительный объемный заряд, а электроны, перешедшие в правую часть кристалла, образуют отрицательный объемный заряд равной величины, в результате чего в объеме кристалла полупроводника вдоль оси X образуется постоянное по величине электрическое поле E_х (см. рис.3).

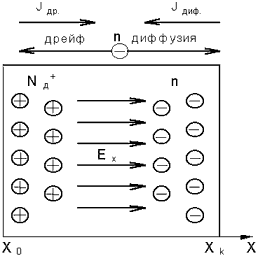
Рис. 3. Распределение объемных зарядов в кристалле

Силы электрического поля будут стремиться возвращать электроны в ту область кристалла, откуда они диффундировали. Те электроны, энергия которых недостаточна для преодоления сил электрического поля, будут возвращаться – дрейфовать в электрическом поле в направлении, противоположном процессу диффузии.

Таким образом, в кристалле полупроводника вдоль оси X текут два встречно направленных тока: J_диф. – ток диффузии, J_др. – ток дрейфа.

В процессе образования электрического поля в кристалле в сторону увеличения его напряженности, диффузионный ток уменьшается вследствие снижения градиента концентрации электронов, а дрейфовый ток увеличивается за счет увеличения количества электронов, возвращаемых растущим полем в обратную сторону, что в конечном итоге приводит к выравниванию этих токов J_диф.=J_др. и установлению в объеме кристалла электрического и термодинамического равновесия.

Плотность тока диффузии: J_диф. = –q_nD(dn/dx).

Плотность тока дрейфа: J_др. = μnq_nE_x .

Суммарный ток в кристалле:

J_k = J_др. + J_диф. = μnq_nE_x – q_nD(dn/dx) = 0.

Исходя из вышеизложенного, напряженность электрического поля в кристалле:

E_x = (kT / q_n) K,

где: k – постоянная Больцмана, T – абсолютная температура кристалла, q_n – заряд основных носителей, K – показатель экспоненты распределения примеси.

Таким образом, неоднородное распределение донорной примеси N_д вдоль оси X кристалла полупроводника по экспоненциальному закону приводит к образованию в объеме кристалла полупроводника постоянного по величине электрического поля, величина напряженности которого E_x не зависит от координаты X, а определяется только величиной абсолютной температуры T кристалла и показателем K экспоненты распределения донорной примеси. При этом один конец полупроводника (X₀) окажется заряженным положительно по отношению к другому концу полупроводника (X_k).

В этом случае, при заданной температуре, диаграмма энергетических зон в полупроводнике вдоль оси X приобретает следующий вид (см. рис.4)

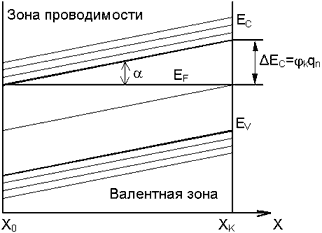
Рис. 4. Диаграмма энергетических зон

ΔE_с – высота потенциального барьера между концами полупроводникового кристалла, φ_k – разность потенциалов между концами полупроводникового кристалла, α – угол наклона энергетических зон.

tgα = q_nE_x .

Это означает, что между противоположными концами полупроводникового кристалла существует разность потенциалов, φ_k а значит, развивается ЭДС (холостого хода).

ЭДС, выраженная в Вольтах будет по величине численно равна половине ширины запрещенной зоны полупроводника:

ЭДС = (E_c – E_v) / 2 (B).

Например, для германия ЭДС_Gе = 0,35В, для кремния ЭДС_Si = 0,55В при температуре 293ºК.

Если замкнуть разноименные концы полупроводникового кристалла металлическим проводником с сопротивлением R, то в цепи потечет электрический ток J_R, и как следствие в кристалле нарушится электрическое и термодинамическое равновесие, а именно: электроны уйдут с правого конца кристалла и перейдут в левый конец кристалла через проводник, чем будет увеличен градиент концентрации электронов, а значит ток диффузии J_диф.. увеличится, а ток дрейфа J_др. уменьшится, так как уменьшится напряженность электрического поля E_х.

Ток J_R в проводнике будет составлять разницу между токами диффузии J_диф. и дрейфа J_др.:

J_R = J_диф. – J_др..

При увеличении тока диффузии электроны будут отбирать тепловую энергию от кристаллической решетки полупроводника, вследствие преодоления ими потенциального барьера ΔЕ_с, в результате чего кристалл будет охлаждаться. Для поддержания постоянного тока в цепи нагрузки необходимо непрерывно подводить к кристаллу теплоту Q от окружающей среды (воздух, вода и т.п., см. рис.5).

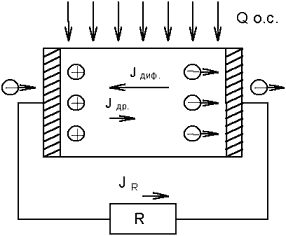
Рис. 5. Электрическая схема полупроводникового преобразователя

Аналогичные рассуждения и выводы можно сделать при легировании кристалла полупроводника акцепторной примесью (N_a) или встречно легировать донорной и акцепторной примесями (N_д – N_a).