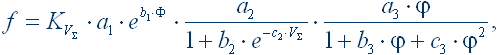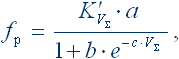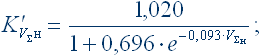Простая формула для определения коэффициента трения в смазываемых дисковых вариаторах
Нурбей Гулиа, Дмитрий Ковчегин, Сергей Юрков, Екатерина Петракова
Одним из важнейших вопросов, возникающих при конструировании смазываемых фрикционных вариаторов, является обоснованный выбор коэффициента трения в рабочих зонах фрикционных контактов. Надо отметить, что трение в этих фрикционных контактах существенно отличается от обычного сухого или граничного трения и лишь условно может быть охарактеризовано как трение.
При нагружении фрикционного контакта силами нормального давления и вращении самих рабочих тел (катков) возникает очень кратковременное, порядка тысячных долей секунды, и существенное давление – до тысяч мегапаскалей, сдавливание жидкого смазочного материала (ЖСМ) в зонах контакта. При таком характере нагружения ЖСМ – минеральное масло, или в еще большей степени специальные высоко-тяговые жидкости (трактанты), переходят в состояние, близкое к упруго-вязкому твердому телу, и начинают передавать существенные тангенциальные нагрузки (1).
Чаще всего коэффициент трения fp определяют по известной формуле О.Г.Ромашкина (2), полученной на основе испытаний вариатора Е.И.Пирожкова:
fp = Км(a/b)–0,2919ρy–0,0631σн0,4865V1–0,4749VΣ–0,3103, | (1) |
где Км – коэффициент, зависящий от типа ЖСМ, заливаемого в вариатор (Км=0,002 для минеральных масел; Км=0,0035 для трактантов); a и b – оси эллипса пятна контакта; ρy – приведенный радиус кривизны фрикционных дисков в направлении вектора скорости качения; σн – контактные напряжения в нижнем и верхнем контактах; V1 – наибольшая в направлении вектора скорости качения скорость геометрического скольжения; VΣ – суммарная скорость качения в контакте.
Однако экспериментальные исследования планетарного дискового вариатора показали, что формула (1) дает расхождения на 50% и выше при низких суммарных скоростях качения VΣ. Это вызвано как особенностями контакта Байера по сравнению с фрикционным контактом вариатора Е.И.Пирожкова, так и тем, что испытания проводились в достаточно узком диапазоне весьма высоких VΣ=36...52м/с. Аппроксимация экспериментальных данных проводилась только для этого диапазона и вне его расхождения получаются существенными.
Н.В.Гулиа и С.А.Юрковым в (3) были предложены формулы для определения коэффициентов УГД-трения, учитывающая большое число факторов, не учитываемых в формуле О.Г.Ромашкина, в частности, влияние фактора верчения. Этот фактор, несколько снижающий коэффициент УГД-трения при малых и больших передаточных отношениях вариатора, особенно характерен для фрикционных контактов Байера в дисковых вариаторах.
Упомянутые формулы для определения коэффициентов УГД-трения представлены ниже:
| (2) |
где KV∑ – поправочный коэффициент, учитывающий влияние суммарных скоростей качения; a1, a2, a3, b1, b2, b3, c1, c2, c3 – коэффициенты; Ф – фактор верчения; φ – относительная скорость геометрического скольжения.
Для минерального масла коэффициент a1=0,045 в нижнем контакте, a1=0,037 в верхнем контакте; b1=–0,7. Остальные коэффициенты приведены в (3).
Поправочный коэффициент KV∑ определяется по формуле:
для нижнего контакта
| (3) |
для верхнего контакта
| (4) |
Но для более точного соответствия эксперименту, причем с учетом физического соответствия реальному процессу передачи крутящего момента вариатором, были приняты следующие допущения.
1. Характер влияния типа ЖСМ, его температуры и контактных напряжений на коэффициент УГД трения в роликовых стендах и в вариаторе достаточно близок друг к другу. Это соответствует мировой практике конструирования вариаторов, где материалы стендовых исследований закладывают в исходные данные при расчете вариаторов.
2. Влияние трения верчения и проскальзывания на коэффициент УГД трения в планетарном дисковом вариаторе в большой степени компенсирует друг друга практически во всем диапазоне передаточных отношений. Это было подтверждено расчетами и, как будет видно в дальнейшем, экспериментов.
В результате для расчета реальных коэффициентов УГД трения получилась простая формула
| (5) |
где a, b, c – коэффициенты влияния суммарной скорости на коэффициент УГД-трения в зависимости от температуры используемого типа ЖСМ и контактных напряжений.
Поправочный коэффициент KV∑ для (5) определяется по формуле:
для нижнего контакта
| (6) |
для верхнего контакта
| (8) |
Коэффициент KVΣ характеризует тип и вид фрикционного контакта (внешний или внутренний), а также влияние скорости VΣ на эти факторы.
В таблице1 приведены значения a, b и с для двух типов ЖСМ – трактанта «Сантотрак-50» и минерального масла при температурах 50°С и 100°С, при контактных напряжениях σн от 782 до 1565МПа. Это наиболее характерные условия работы вариаторов, для которых имеется достаточно большой экспериментальный материал.
Таблица 1
| Тип ЖСМ | Температура ЖСМ T, °С | Контактные напряжения σн, МПа | Коэффициенты | ||
| a | b | c | |||
| Сантотрак-50 | 50 | 782 | 0,0470 | –0,5866 | 0,0235 |
| 1100 | 0,0626 | –0,4943 | 0,0468 | ||
| 1355 | 0,0602 | –1,3563 | 0,0282 | ||
| 1565 | 0,0526 | –0,4280 | 0,0233 | ||
| 100 | 782 | 0,0563 | –0,5790 | 0,0254 | |
| 1100 | 0,0669 | –0,4998 | 0,0436 | ||
| 1355 | 0,0683 | –0,3719 | 0,0596 | ||
| 1565 | 0,0566 | –0,4537 | 0,0307 | ||
| Минеральное масло | 50 | 782 | 0,0309 | –0,7977 | 0,0652 |
| 1100 | 0,0394 | –0,5914 | 0,0444 | ||
| 1355 | 0,0306 | –0,5984 | 0,0240 | ||
| 1565 | 0,0356 | –0,5404 | 0,0235 | ||
| 100 | 782 | 0,0241 | –0,8359 | 0,0191 | |
| 1100 | 0,0283 | –0,7494 | 0,0165 | ||
| 1355 | 0,0351 | –0,6432 | 0,0215 | ||
| 1565 | 0,0404 | –0,5514 | 0,0275 | ||
Промежуточные значения коэффициентов а, b и c могут быть получены интерполированием, например, с помощью соответствующих графиков.
На графиках рис.1 приведены значения fp для внутреннего и внешнего контактов по данным испытаний вариатора (4) для частоты вращения входа n1=1460мин–1 – сплошная линия и по формуле (5) – штриховая линия.
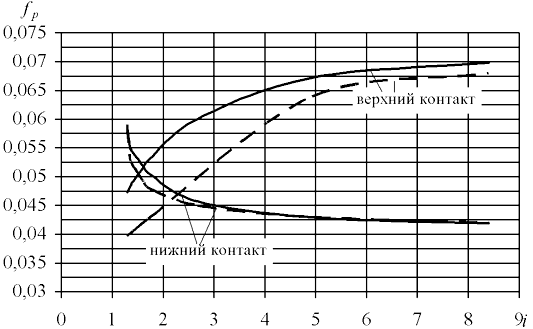
Рис.1. Зависимость коэффициентов трения fp от передаточного отношения i при частоте вращения входа n1=1460мин–1 и смазке минеральным маслом: сплошная линия – по данным испытаний; пунктирная линия – по формуле (5)
На рис.2 – то же для ЖСМ «Сантотрак-50». На рис.3 и 4 приведены те же данные, но для n1=2850мин–1.
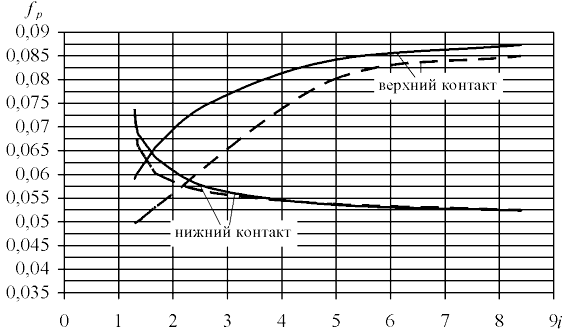
Рис.2. Зависимость коэффициентов трения fp от передаточного отношения i при частоте вращения входа n1=1460мин–1 и смазке трактантом «Сантотрак-50»: сплошная линия – по данным испытаний; пунктирная линия – по формуле (5)
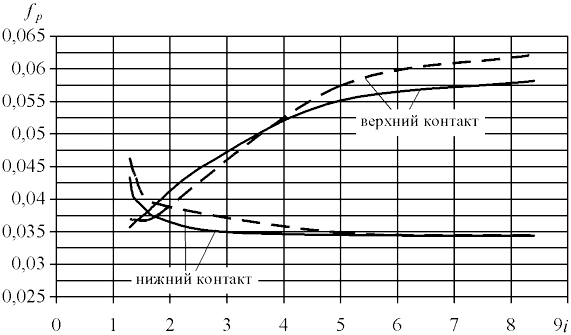
Рис.3. Зависимость коэффициентов трения fp от передаточного отношения i при частоте вращения входа n1=2850мин–1 и смазке минеральным маслом: сплошная линия – по данным испытаний; пунктирная линия – по формуле (5)
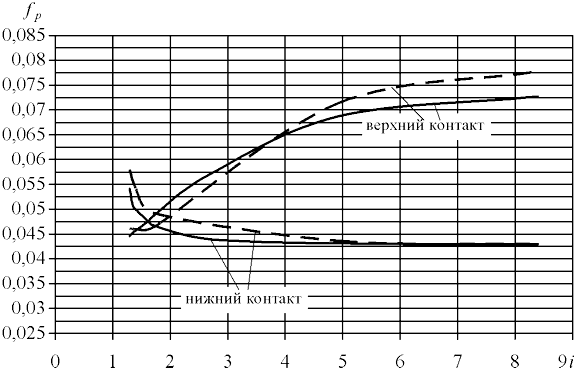
Рис.4. Зависимость коэффициентов трения fp от передаточного отношения i при частоте вращения входа n1=2850мин–1 и смазке трактантом «Сантотрак-50»: сплошная линия – по данным испытаний; пунктирная линия – по формуле (5)
Отметим, что предложенная формула (5) проще всех остальных известных формул для определения коэффициента трения смазываемых вариаторов и достаточно адекватно отражает данные экспериментов. Учитывая, что в экспериментах были получены практически максимальные значения коэффициентов трения fp, значения коэффициентов трения, полученные из (5), как, собственно, и из (1), при использовании их на практике необходимо разделить на величину коэффициента запаса по сцеплению β=1,25...1,5.
Заметим, что для весьма низких скоростей VΣ, которые имеют место в верхнем контакте при малых передаточных отношениях и частотах вращения (рис.1 и 2) могут иметь место случаи граничного трения, повышающие коэффициент трения при испытаниях, но не вполне отражающие картину чистого УГД-трения. С увеличением частоты вращения, а, следовательно, и VΣ, расчетные данные практически совпадают с данными испытаний (рис.3 и 4). Здесь поверхности качения уже полностью разделены пленкой ЖСМ и имеет место чистое УГД-трение.
ЕлмановИ.М., КолесниковВ.И. Термовязкоупругие процессы трибосистем в условиях упругогидродинамического контакта. – Ростов-на-Дону: Центр Высшей школы, 1999. – 173с.
РомашкинО.Г. О влиянии геометрии основного контакта фрикционной бесступенчатой передачи на коэффициент трения // Трение и износ. – 1986. –Т.7. – №5. – С.894...899.
ГулиаН.В., ЮрковС.А. Определение коэффициента упругогидродинамического трения в зонах контактов фрикционных вариаторов при наличии верчения // Тр. МГИУ. – 2001. – С.38...47.
ГулиаН.В., КовчегинД.А., ЮрковС.А. Основные экспериментальные характеристики нового адаптивного вариатора. НиТ, 2002.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Проблема эволюции Вселенной
Борис ЯкушевПроблема эволюции Вселенной является центральной в естествознании. Она привлекает к себе исследователей различных специ
- Применение лазера в опыте Майкельсона – Морли
Валерий ПетровВ своей работе «К электродинамике движущихся сред» А.Эйнштейн указал, что распространению принципа относительности на
- Осторожно, тяжелая вода
М. АджиевТяжелая вода очень дорога и дефицитна. Однако если удастся найти дешевый и практичный способ ее получения, то области применен
- Пассивная адаптивность и «живучесть» фрикционного вариатора
Нурбей Гулиа, Дмитрий Ковчегин, Сергей Юрков, Екатерина ПетраковаИспытания нового планетарного дискового вариатора (пат. РФ№2140028, авто
- В поисках инерцоида
Владимир ОколотинМногие века люди относились к массивным телам как своеобразным складам движения – сколько в них вложишь, столько и в
- Явления, обусловленные движением Земли относительно мирового эфира
Валерий ПетровЭйнштейн предполагал, что все попытки обнаружить движение Земли относительно мирового эфира оказались безуспешными. Бе
- Постчеловеческая цивилизация
Александр БолонкинПринцип возрастания хаоса во ВселеннойВ связи с развитием теплотехники ученые в прошлом веке пришли к простому, но
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.