Оптимальные и адаптивные системы
![]() - корни вещественные
- корни вещественные
![]()
![]()
Сумма двух экспонент представляет собой:
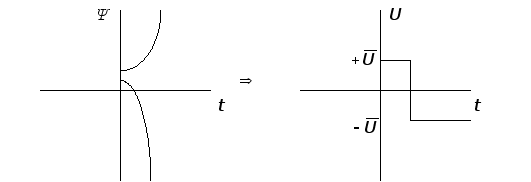
Если ![]() , то корни комплексно-сопряженные и решение будет представлять собой периодическую функцию. В реальной системе, переключений не более 5 - 6.
, то корни комплексно-сопряженные и решение будет представлять собой периодическую функцию. В реальной системе, переключений не более 5 - 6.
Метод поверхности переключений
Данный метод позволяет найти управление функций переменной состояния для случая когда оптимальное управление носит релейный характер
![]() .
.
Таким образом этот метод можно применять при решении задач оптимального быстродействия, для объекта с аддитивным управлением
![]() ,
,
![]() .
.
Суть метода заключается в том, чтобы во всём пространстве состояний выделить точки, где происходит смена знака управления и объединить их в общую поверхность переключений.
![]() ,
,
![]() - поверхность переключений
- поверхность переключений
![]() .
.
Закон управления будет иметь следующий вид
![]() .
.
Для формирования поверхности переключений удобнее рассматривать переход из произвольной начальной точки в начало координат
![]() .
.
Если конечная точка не совпадает с началом координат, то необходимо выбрать новые переменные, для которых это условие будет справедливо.
Имеем объект вида
![]() .
.
Рассматриваем переход ![]() , с критерием оптимальности
, с критерием оптимальности
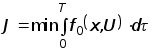 .
.
Этот критерий позволяет найти закон управления такого вида
![]() ,
,
с неизвестным ![]() , начальные условия
, начальные условия ![]() нам также неизвестны.
нам также неизвестны.
Рассматриваем переход:
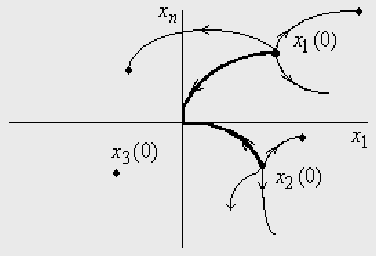
Метод обратного времени
(метод попятного движения)
Этот метод позволяет определить поверхности переключений.
Суть метода заключается в том, что начальная и конечная точки меняются местами, при этом вместо двух совокупностей начальных условий остаётся одна для ![]() .
.
Каждая из этих траекторий будет оптимальна. Сначала находим точки, где управление меняет знак и объединяем их в поверхность, а затем направление движения меняем на противоположное.
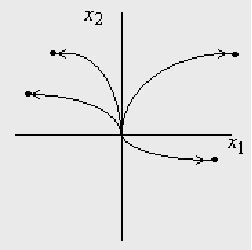
Пример
Передаточная функция объекта имеет вид
![]() .
.
Критерий оптимальности быстродействия
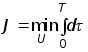
Ограничение на управление ![]() .
.
Рассмотрим переход
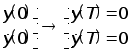 .
.
1)
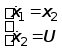 ,
,
2)
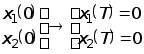 .
.
3)
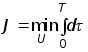
оптимальное управление будет иметь релейный характер
![]() .
.
4) Перейдём в обратное время (т.е. ![]() ). В обратном времени задача будет иметь такой вид
). В обратном времени задача будет иметь такой вид
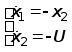 .
.
5) Рассмотрим два случая:
Получим уравнения замкнутой системы
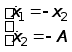 .
.
Воспользуемся методом непосредственного интегрирования, получим зависимость ![]() от
от ![]() и поскольку
и поскольку ![]() -
-![]() , то имеем
, то имеем
![]() ,
,
т.к. начальные и конечные точки поменяли местами, то ![]() ,
, ![]() получим
получим
![]() , (*)
, (*)
аналогично
![]()
![]()
подставив (*), получим
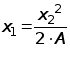 ,
,
отсюда
![]() .
.
Построим получившееся и по методу фазовой плоскости определим направление
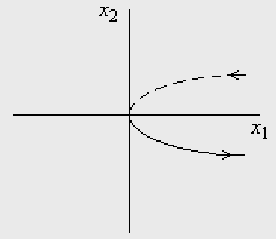
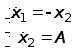
Применив метод непосредственного интегрирования, получим:
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]() .
.
Функция будет иметь вид:
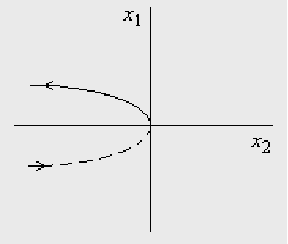
Изменив направление
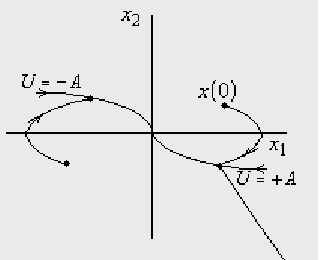
точка смены знака
(точка переключения)
Общее аналитическое выражение:
![]() .
.
Уравнение поверхности:
![]() .
.
Оптимальный закон управления:
![]() ,
,
подставив уравнение поверхности, получим:
![]() .
.
2.5. Субоптимальные системы
Субоптимальные системы - это системы близкие по свойствам к оптимальным
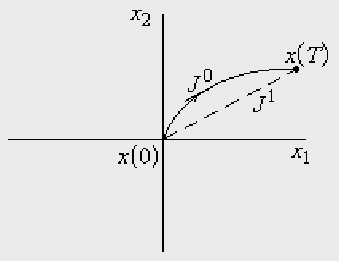
![]() - характеризуется критерием оптимальности.
- характеризуется критерием оптимальности.
![]()
![]() - абсолютная погрешность.
- абсолютная погрешность.
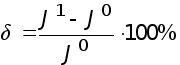 - относительная погрешность.
- относительная погрешность.
Субоптимальным называют процесс близкий к оптимальному с заданной точностью.
Субоптимальная система - система где есть хоть один субоптимальный процесс.
Субоптимальные системы получаются в следующих случаях:
при аппроксимации поверхности переключений (с помощью кусочно-линейной аппроксимации, аппроксимация с помощью сплайнов);
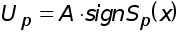
при
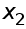 в субоптимальной системе будет возникать оптимальный процесс.
в субоптимальной системе будет возникать оптимальный процесс.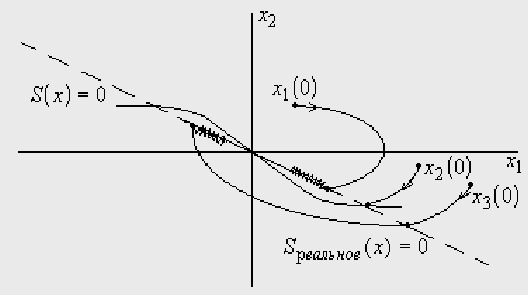
ограничение рабочей области пространства состояний;
![]()
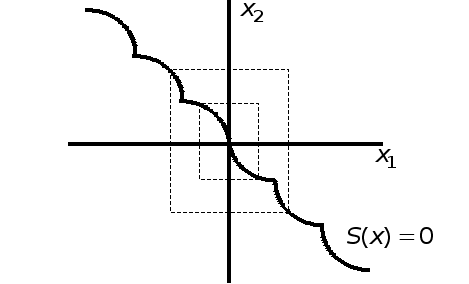
3.АДАПТИВНЫЕ СИСТЕМЫ
3.1.Основные понятия
Адаптивными системами называют такие системы, в которых параметры регулятора меняются вслед за изменением параметров объекта, таким образом, чтобы поведение системы в целом оставалось неизменным и соответствовало желаемому:
![]() ,
,
![]() .
.
Существует два направления в теории адаптивных систем:
адаптивные системы с эталонной моделью (АСЭМ);
адаптивные системы с идентификатором (АСИ).
Адаптивные системы с идентификатором
Идентификатор - устройство оценки параметров объекта (оценка параметров должна осуществляться в реальном времени).

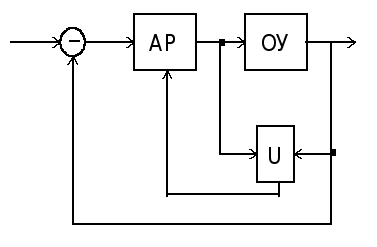
АР - адаптивный регулятор
ОУ - объект управления
U - идентификатор
Часть, которая выделена пунктиром, может быть реализована в цифровом виде.
Рис1. Функциональная схема АСИ
V, U, X - могут быть векторы. Объект может быть многоканальным.
Рассмотрим работу системы.
В случае неизменных параметров объекта, структура и параметры адаптивного регулятора не меняются, действует главная обратная связь, система представляет собой систему стабилизации.
Если параметры объекта меняются, то они оцениваются идентификатором в реальном времени и происходит изменение структуры и параметров адаптивного регулятора так, чтобы поведение системы оставалось неизменным.
Основные требования предъявляются к идентификатору (быстродействие и т.д.) и к самому алгоритму идентификации.
Такой класс систем используют для управления объектами с медленными нестационарностями.
Если мы имеем нестационарный объект общего вида:
![]() ,
,
![]() ,
, ![]() .
.
Простейший адаптивный вид будет следующий:
![]() .
.
Требования, которые предъявляются к системе:
![]() , (*)
, (*)
![]() ,
,
где ![]() и
и ![]() - матрицы постоянных коэффициентов.
- матрицы постоянных коэффициентов.
Реально мы имеем:
![]()
или
![]() (**)
(**)
Если приравнять (*) и (**), то получим соотношение для определения параметров регулятора
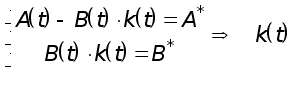
3.3.Адаптивные системы с эталонной моделью
В таких системах существует эталонная модель (ЭМ), которая ставится параллельно объекту.
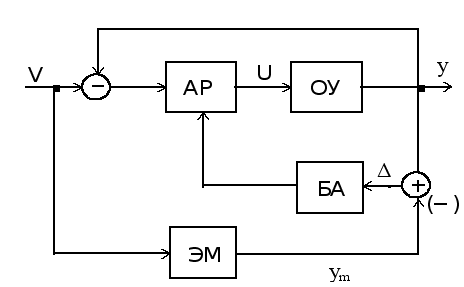
БА - блок адаптации.
Рис2. Функциональная схема АСЭМ
Рассмотрим работу системы.
В том случае, когда параметры объекта не меняются или процессы на выходе соответствуют эталонным, ошибка ![]() , не работает блок адаптации и не перестраивается адаптивный регулятор, в системе действует плавная обратная связь.
, не работает блок адаптации и не перестраивается адаптивный регулятор, в системе действует плавная обратная связь.
Если поведение отлично от эталонного, это происходит при изменении параметров объекта, в этом случае появляется ошибка ![]() , включается блок адаптации, перестраивается структура адаптивного регулятора, таким образом чтобы свести к эталонной модели объекта.
, включается блок адаптации, перестраивается структура адаптивного регулятора, таким образом чтобы свести к эталонной модели объекта.
Блок адаптации должен сводить ошибку к нулю (![]() ).
).
Алгоритм, закладываемый в блок адаптации, формируется различными способами, например, с использованием второго метода Ляпунова:
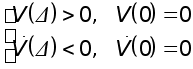 .
.
Если это будет выполняться, то система будет асимптотически устойчива и ![]() .
.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Оптические датчики газового состава
Московский ордена Ленина, ордена Октябрьской Революции и ордена Трудового Красного Знамени ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ и
- Оптические и магнитооптические системы
Государственный Комитет Российской Федерациипо Высшему образованию Красноярский Государственный Технический УниверситетКафедра выч
- Організація ремонту машино-тракторного парка з технологічною розробкою ЦРМ господарства
Тема: ""(Украина) Раздел: Технология Назначение: Курсовая работа, как составляющая часть дипломного проекта Формат: WinWord Автор: Думенко Ко
- Организация и планирование монтажа систем ТГСВ (монтаж наружных тепловых сетей)
- Организация и технология процесса в розничной торговой сети
Устройство и технологическая планировка магазинов и их влияние на результат хозяйственной деятельности торгового предприятия.УСТРОЙС
- Организация конструкторской подготовки производства
Основныезадачи, стадиииэтапы проектно-конструкторскойподготовкиОсновной задачей проектно-конструкторской подготовки производства я
- Организация производства на основе выбора ассортимента
Министерство общего и профессионального образования Российской Федерации Московская Государственная Текстильная Академия им. А.Н.Кос
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

