Скачать

Определитель произведения прямоугольных матриц. Теорема Коши-Бине

Курсовая работа

Выполнила студентка II курса группы ПМИ Решоткина Наталья Николаевна

Мурманский Государственный Педагогический Университет

Мурманск 2007

Введение

При решении различных задач математики очень часто приходится иметь дело с таблицами чисел, называемых матрицами. С помощью матриц удобно решать системы линейных уравнений, выполнять многие операции с векторами, решать различные задачи компьютерной графики и другие инженерные задачи.

Цель данной работы: теоретическое обоснование и необходимость практического применения теоремы Коши-Бине:

Пусть , - и -матрицы соответственно, и

Тогда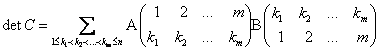

Другими словами, при определитель матрицы является суммой произведений всевозможных миноров порядка в на соответствующие миноры матрицы того же самого порядка

Работа состоит из четырех глав, содержит заключение, список литературы и приложение программы для теоремы Коши-Бине. В главе I рассматриваются элементы линейной алгебры – матрицы, операции над матрицами и свойства сложения матриц, и умножения на скаляр. Глава II посвящается умножению матриц и его свойств, а также транспонирование произведения двух матриц. В главе III рассматриваются обратимые и элементарные матрицы. В главе IV вводиться понятие определителя квадратной матрицы, рассматриваются свойства и теоремы об определителях, а также приводится доказательство теоремы Коши-Бине, что является целью моей работы. В дополнение прилагается программа показывающая механизм нахождения определителя произведения двух матриц.

Глава I

§ 1 Определение, обозначения и типы матриц

Мы определяем матрицу как прямоугольную таблицу чисел:

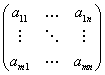
Где элементы матрицы aij (1≤i≤m, 1≤j≤n)-числа из поля .Для наших целей поле будет либо множеством всех вещественных чисел, либо множеством всех комплексных. Размер матрицы , где m-число строк, n-число столбцов. Если m=n, то говорят, что матрица квадратная, порядка n. В общем случаем матрица называется прямоугольной.

Каждой матрице с элементами aij соответствует n×m матрица с элементами aji . Она называется транспонированной к и обозначается через. Видно, что =. Строки матрицы становятся столбцами в и столбцы матрицы становятся строками в.

Матрица называется нулевой если все элементы равны 0:

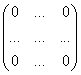
Матрица называется треугольной если все ее элементы, расположенные ниже главной диагонали равны 0

Треугольная матрица называется диагональной, если все элементы расположенные вне главной диагонали равны 0

Диагональной матрица называется единичной, если все элементы расположенные на главной диагонали равны 1

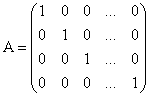
Матрица, составленная из элементов, находящихся на пересечении нескольких выбранных строк матрицы и нескольких выбранных столбцов, называется субматрицей для матрицы . Если -номера выбранных строк и -номера выбранных столбцов, то субматрица это

В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.

§2 Операции над матрицами

Определим следующие операции:

Сумма двух матриц , и с элементами и есть матрица С с элементами , запишем это как

Произведение матрицы на число поля есть матрица С с элементами , запишем как .

Произведение матрицы на матрицу есть матрица С с элементами , запишем

поле скаляров, рассмотрим 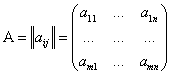, где элемент матрицы , расположенный в -строке , -столбце . Размерность матрицы .Если , то -квадратная матрица порядка . Множество -это множество всех матриц над полем .

Опр. Две матрицы равны, если они имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы. Другими словами: равна матрице , т.е

Опр. Пусть -это матрицы одинаковой размерности . Суммой матриц и называется матрица у которой в строке, столбце расположен элемент , т.е. . Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:

Пример:

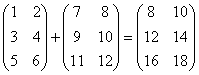
Опр. Пусть , , . Произведение скаляра на матрицу называется у которой в строке, столбце расположен элемент . Другими словами: Чтобы скаляр умножить на матрицу нужно все элементы матрицы умножить на скаляр .

Определение. Противоположной к матрице называется матрица

Свойства сложения и умножения матриц на скаляры:

-абелева группа

1) Сложение матриц ассоциативно и коммутативно.

2)

3)

а)

б)

4)

Глава II

§1 Умножение матриц

,

,

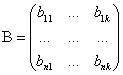
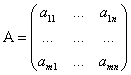Опр. Произведением матрицы на матрицу называется матрица . , где

, где

Говорят, что есть скалярное произведение -строки матрицы на -столбец матрицы .

, где

Пример:

§2 Свойства умножения матриц

Умножение матриц ассоциативно:

1) , если определены произведения матриц и

Доказательство:

Пусть , так как определено , то и определено , то

Определим матрицы:

а)

б)

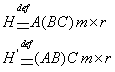(1) матрицы, тогда имеют одинаковую размерность

2) Покажем, что на одинаковых местах в матрицах расположены одинаковые элементы

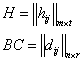из равенства (1) (2), (3). Подставляя (3) в (2) получим:

, тогда (4), (5). Подставляя (5) в (4) получим:

Вывод: Матрицы имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы.

Умножение матриц дистрибутивно :

Доказательство:

так как определено , то и определено , то

размерности

размерности

Матрицы имеют одинаковую размерность, покажем расположение одинаковых элементов:

,

,

Вывод: На одинаковых местах расположены одинаковые элементы.

3. , . Если определены матрицы, то доказательство проводим аналогично свойству 2.

4. , : , если определена матрица

Доказательство:

. Пусть ,

, ,

5. Умножение матриц в общем случае не коммутативно. Рассмотрим это на примере:

, тогда

§3 Техника матричного умножения

поле скаляров, ,

Свойства:

Произведение можно рассматривать, как результат умножения столбцов матрицы на слева и как результат умножения строк матрицы на справа.

Пусть матрица , -линейная комбинация столбцов матрицы коэффициенты которой служат элементы матрицы

Пример

Пусть -матрица , тогда -линейная комбинация строк матрицы коэффициенты которой служат элементы матрицы

Пример:

Столбцы матрицы -линейная комбинация столбцов матрицы . Строки -линейная комбинация строк матрицы .

§4 Транспонирование произведения матриц

поле скаляров, , , ,

Теорема

если , то . Обозначим: ,

Доказательство:

1) Пусть ,

- размерности ,- размерности , тогда и имеют одинаковую размерность

2) , -элемента расположенный в -строке, -столбце матрицы т.е

, -произведение -строки транспонированной на столбец ,

Глава III

§1 Обратимые матрицы

поле скаляров, множество матриц порядка

Определение. Квадратная матрица порядка называется единичной матрицей ,

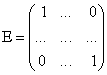
Пусть ,

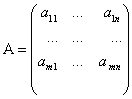
Теорема 1

, то для выполняется

Доказательство:

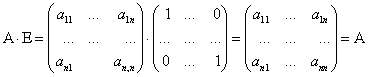
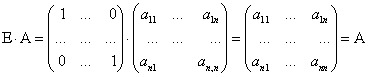
Из этого следует . Матрица является единичной матрицей. Она выполняет роль единицы при умножении матриц.

Определение. Квадратная матрица называется обратимой если существует так, что выполняются условия

Матрица называется обратной к и обозначается , тогда если -это обратная к , то обратная к -это взаимообратные матрицы т.е.

Теорема 2

Если -обратима, то существует только одна матрица обратная к

Доказательство:

Пусть дана матрица , которая обратима и пусть существуют матрицы обратные к т.е. . Имеем