Скачать

Теория Вероятностей

Оглавление

Введение

1.Алгебра событий

2.Вероятность

3.Формула Бейеса

4.Формула полной вероятности

5.Пример задачи для формулы полной вероятности

6.Пример задачи для формулы Бейеса

7.Геометрические вероятности

Введение

Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля. Позднее развитие теории вероятностей определились в работах многих ученых. Большой вклад в теорию вероятностей внесли ученые нашей страны: П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.

Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей. Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.

1.Алгебра событий.

В теории вероятностей под событием понимают то, относительно чего после некоторого момента времени можно сказать одно и только одно из двух: Да, оно произошло.

Нет, оно не произошло.

Например, у меня есть лотерейный билет. После опубликования результатов розыгрыша лотереи интересующее меня событие – выигрыш тысячи рублей либо происходит, либо не происходит.

События принято обозначать заглавными латинскими буквами: A,B,C,…. С событиями можно совершать операции. Эти операции являются основой алгебры событий. Объединением двух событий С=АВ называется событие С, которое происходит тогда и только тогда, когда происходит хотя бы одно из этих событий А и В. Пересечением двух событий D=АВ называется событие, которое происходит тогда и только тогда, когда происходят и А и В. Противоположным событием А* к событию А называется такое событие, которое происходит тогда и только тогда, когда не происходит событие А. Объединением C событий A1,A2,…Ak называется событие C=Ai, которое осуществляется тогда и только тогда, когда осуществляется хотя бы одно из событий Ai,i=1,…,k. Пересечением D событий A1,…,Ak называется событие D=∩Ai, которое осуществляется тогда и только тогда, когда осуществляются все события Ai,i=1,…,k. Разностью событий G=AB называется событие, которое происходит тогда и только тогда, когда происходит событие А, но не происходит событие В.

Среди событий особое место занимают невозможное событие и достоверное событие. Невозможное событие – это такое событие, о котором заранее известно, что оно произойти не может. Его обозначают символом . Достоверное событие – это такое событие, о котором заранее известно, что оно произойдет. Его обозначают буквой Ω.

События A и B называются не пересекающимися, если одновременно не могут осуществиться и событие A и событие B. В таких случаях также говорят, что пересечение A∩B есть невозможное событие .

Некоторую совокупность L событий называют алгеброй событий, если она удовлетворяет следующим условиям. Эта совокупность L содержит невозможное событие и достоверное событие . Если L содержит некоторое событие А, то она содержит и противоположное событие А*. Если совокупность L содержит некоторые события A1,A2,…,Ak, то она содержит и объединение С=Ai и пересечение D=∩Аi этих событий.

Например, алгеброй событий L является самая скудная такая алгебра, которая состоит всего из двух событий: из невозможного события и достоверного события . В самом деле, сколько бы мы ни составляли объединений и пересечений из этих событий, и сколько бы мы ни брали противоположных событий, мы не получим ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,.

2.Вероятность.

Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только после этого момента реализуется определенность: Да, событие А произошло, или наоборот Нет, событие А не произошло, т.е. произошло событие А*.

Каждому из рассматриваемых случайных событий приписывается число P,0≤P≤1(P(A),P(B),P(C),…), которое называется его вероятностью. Это число характеризует шансы, что соответствующее событие произойдет. На практике для интересующих событий числа P назначаются, исходя из опыта и здравого смысла. Когда говорят о событиях, оговаривают обстоятельства, при которых рассматриваются эти события.

Принимают, что Р(Ω)=1, Р()=0. Если события A1,A2,…,Ak попарно не пересекаются, то полагают Р(Ai)=Р(A1)+Р(A2)+…+Р(Ak). Поэтому Р(A)+Р(A*)=1.

Например, если подбрасывается хорошо сбалансированная монета, то вероятность того события A, что она упадет орлом вверх принимается равной 1/2, а вероятность противоположного события A*, то есть того, что она упадет решкой вверх, принимается тоже равной 1/2. При этом событие, состоящее в том, что монета встанет и останется стоять на ребре, принимается за невозможное. Если бросают игральную кость, то вероятность того, что выпадет, например, четыре очка, принимается равной 1/6. Вероятность противоположного события, то есть того, что выпадет какое-либо число очков, не равное четырем, принимается равной 5/6. Если из хорошо перетасованной колоды в пятьдесят две карты вынимают наугад одну карту, то вероятность того, что вынут короля, равна 4/52=1/13 и т. д.

Говорят, что некоторое событие B благоприятствует событию A, если всякий раз как происходит событие B, происходит и событие A. Принимают следующее соглашение. Если из n всех возможных непересекающихся равновозможных событий, то есть таких, для которых вероятности полагаются равными, некоторому событию A благоприятствует m из таких равновозможных случаев, то принимают

Р(A)=m/n.(2.1)

В приведенном выше примере с колодой карт имеется n=52 равновозможных события: вынут одну какую-нибудь карту. Событию A–тому, что вынут короля, благоприятствуют m=4 события: B1–вынут короля пик, B2–короля треф, B3–короля бубен, B4–короля червей. И только такие события Bi благоприятствуют событию A. При этом A есть объединение событий Bi: A=UBi и события Bi и Bj не пересекаются: Bi∩Bj=,i≠j. Поэтому и принимают Р(А)=m/n=4/52=1/13.

Данное определение вероятности через благоприятствующие равновозможные непересекающиеся события называют часто классическим определением вероятности. Оно подтверждается на практике в виде закона больших чисел. Он проявляется следующим образом. Если сделать большое число n* испытаний, в каждом из которых может появиться событие A, то в результате оказывается, что число m* появлений события A оказывается как правило очень близким к величине Р(A), то есть выполняется с вероятностью очень близкой к единице – практически обязательно, с большой степенью точности приближенное равенство

m*/n* ≈ m/n=Р(A)(2.2)

Условной вероятностью события А по событию В называют величину Р(А|В), которая дает равенство Р(А∩В)=Р(A|B)·P(B). Смысл этого определения таков. Условная вероятность оценивает шансы осуществления события А, когда известно, что произошло событие В.

События А и В называются независимыми, если Р(A|B)=P(A). Тогда Р(А∩В)=Р(A)·P(B). Иначе говоря, события А и В независимы, когда вероятность осуществления события А не зависит от того, осуществилось или нет событие В. И наоборот, вероятность осуществления события В не зависит от осуществления события А.

Например, пусть бросают две не связанные друг с другом игральные кости. Пусть событие А–на первой кости выпало 4 очка. Событие В–на второй кости выпало 2 очка. Тогда Р(А)=1/6,Р(В)=1/6. События А и В естественно полагать независимыми. Стало быть, полагаем Р(А|B)=P(A), P(B|A)=P(B) и P(А∩В)=P(A)·P(B)=1/6·1/6=1/36. То есть вероятность события С=А∩В – на первой кости выпало 2 очка и при этом на второй кости выпало 4 очка равна 1/36.

Несколько событий A1,A2,…,Ak называются независимыми в совокупности, если Р(∩Ai)=Р(A1)·Р(A2)·…·Р(Ak). Важно заметить, что из попарной независимости всех событий Аi и Aj, i=1,…,k, j=1,…,k, ij, вообще говоря, не следует независимость событий A1,A2,…,Ak в совокупности. В этом можно убедиться на конкретном примере.

Подчеркнем еще раз, что физической основой для теории вероятностей является следующее статистическое свойство устойчивости частот. Буквой Аобозначим случайное событие, связанное с некоторым повторяющимся опытом. Пусть опыт повторяется n*раз при одинаковых условиях. Пусть *–число появлений событий А. Относительная частота появления событий А определяется формулой

(2.3)

Если неограниченно увеличивать число повторений опыта , то относительная частота будет устойчиво приближаться к некоторой фиксированной величине Р(А) и отклоняться от нее тем меньше и реже, чем больше n*. Эта величина и является вероятностью P события А. Если в теории вероятность Р(А) определена правильно, то оказывается, что теоретическое число Р(А) совпадает с описанным выше практическим пределом. Это обстоятельство и позволяет численно оценивать вероятность случайного события в теории.

3.Формула Бейеса.

Пусть мы знаем вероятности событий А и В: Р(А) и Р(В). И пусть мы знаем условную вероятность события А по В: Р(A|B). Как найти условную вероятность P(B|A). На этот вопрос отвечает формула Бейеса.

Р(B|A)=P(A|B)·P(B)/P(A)(3.1)

Разумеется этой формулой можно пользоваться только при условии, что Р(А)0.

Формула Бейеса выводится из следующих равенств

Р(ВА)=Р(В|A)·P(A)(3.2)

Р(AB)=Р(A|B)·P(B)(3.3)

причем

Р(ВА)=Р(AB)(3.4)

так как пересечение событий В и А очевидно не зависит от порядка, в котором записаны А и В, т.е. ВА=AB. В случае Р(А)=0 принимаю обычно, что Р(В|A) есть величина неопределенная.

4.Формула полной вероятности.

Пусть имеем полную группу из n попарно непересекающихся событий . То есть

, (4.1) , , (4.2)

Пусть мы знаем условные вероятности некоторого события А по Еi: Р(А|Ei) и вероятности Р(Ei), i=1,…,n. Справедлива следующая формула полной вероятности для события А

Р(А)=Р(A|E1)·P(E1)+…+P(A|En)·P(En)(4.3)

Доказательство этой формулы вытекает из следующих равенств

P(A)=P()=P(A(Ei))=P(AE1)+…+P(AEn)=

=Р(A|E1)·P(E1)+…+P(A|En)·P(En)(4.4)

Из элементарной формулы Бейеса (3.1) и формулы полной вероятности (4.3) вытекает следующая более полная формула Бейеса

Р(Еi|A)=P(A|Ei)·P(Ei)/(Р(A|E1)·P(E1)+…+P(A|En)·P(En))(4.5)

5.Пример задачи для формулы полной вероятности.

Задача 5.1.

Пусть имеем три урны с шарами. В первой урне 7 белых и 3 черных шара. Во второй урне 7 белых и 7 черных шаров. В третьей урне 3 белых и 7 черных шаров. Наугад выбрали одну урну. Из этой урны наугад вынули шар.

Какова вероятность, что вынули белый шар?

Решение:

Пусть событие А – вынули белый шар, событие Ei – вынули шар из i-той урны, i=1,2,3. Вероятности P(Ei) полагаем равными, т.е. Р(Ei)=1/3. Вероятность Р(A|E1)=7/10, вероятность Р(А|E2)=7/14=1/2, вероятность Р(А|E3)=3/10. Таким образом по формуле полной вероятности (4.3) имеем

Р(А)=Р(A|E1)·Р(E1)+Р(A|E2)·Р(E2)+Р(A|E3)·Р(E3)=

=(1/3)·(7/10+5/10+3/10)=(1/3)·15/10=1/2(5.1)

Ответ:Вероятность вынуть белый шар равна Ѕ.

6.Пример задачи для формулы Бейеса.

Задача 6.1.

Пусть имеем те же урны с теми же наборами шаров, как и в задаче (5.1). Снова из выбранной наугад урны выбрали наугад шар. Оказалось, что вынули черный шар.

Какова вероятность, что его вынули из третьей урны?

Решение:

Пусть В – событие, состоящее в том, что вынули черный шар. События Ei те же, что и в решении задачи (5.1). Интересующая нас вероятность есть условная вероятность Р(E3|B). По формуле Бейеса (4.5) имеем

Р(Е3|B)=P(B|E3)·P(E3)/(P(B|E1)·P(E1)+P(B|E2)·P(E2)+P(B|E3)·P(E3)) (6.1)

У нас: Р(Ei)=1/3, i=1,2,3, P(B|E1)=3/10, P(B|E2)=1/2, P(B|E3)=7/10. Таким образом, получаем

Р(Е3|B)=(7/10)·(1/3)/((1/3)·(7/10+5/10+3/10))=(7/10)/(15/10)=7/15 (6.2)

Ответ:Вероятность того, что вынули шар из третьей урны, при условии, что шар оказался черным равна 7/15.

7.Геометрические вероятности.

Как сказано выше, вычисление вероятности на основе несовместимых равновозможных событий по формуле (2.1) называют обычно классическим определением вероятности. Однако применяют и другие способы вычисления вероятностей. Рассмотрим здесь геометрический способ вычисления вероятностей. При этом способе случайные события трактуются, как такие события, которые осуществляются, когда случайная точка попадает в ту или иную область на некоторой прямой или на плоскости или в пространстве. Поясним это подробнее на примере плоскости.

Достоверное событие представляется некоторой областью на плоскости. При этом полагается, что случайная точка обязательно попадает в эту область, т.е. обязательно . Невозможное событие представляется пустым множеством точек, т.е. таким множеством точек, которое не содержит ни одной точки. Т.е. случайная точка никак не может оказаться точкой из этого пустого множества. Каждое случайное событие А из рассматриваемой алгебры событий L представляется некоторой областью , т.е. областью , которая содержится в области . Случайное событие А осуществляется тогда и только тогда, когда случайная точка , т.е. тогда и только тогда, когда точка попадает в область . При такой трактовке объединение событий представляется областью , которая складывается из точек, каждая из которых лежит хотя бы в одной из областей и . Пересечение событий представляется областью , которая является общей частью областей и . Противоположное событие А* представляется областью , которая является дополнением к области до области . См. например фиг.7.1.-7.4.

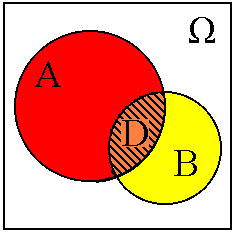
Фиг.7.1.
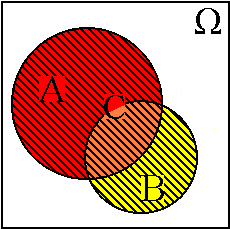
Фиг. 7.2.

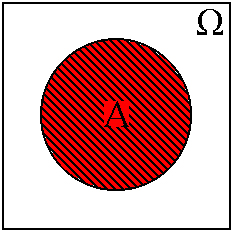
Фиг.7.3.

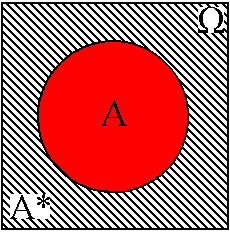
Фиг. 7.4

Предполагая, что для каждой области при любом событии А из алгебры событий L можно определить площадь S этой области полагают вероятность события А равной

Р(А)=S/S(7.1)

Смысл этого определения состоит в том, что для шансов попадания случайной точки в ту или иную точку из области не отдается никакого предпочтения.

Например, пусть область есть квадрат со стороной единица. Событие А состоит в том, что случайная точка попадает в четверть круга с радиусом, равным единице, и вписанного в квадрат . См. фиг.7.5.

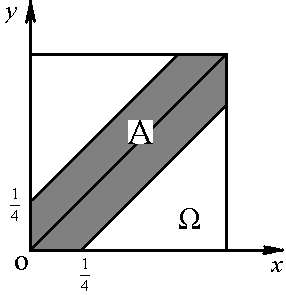
Фиг.7.5.

Тогда по формуле (7.1) получаем

Р(А)=π/4(7.2)

Аналогичные построения делаются, когда за основу берутся области на прямой или области в пространстве. При этом только в случае прямой площади заменяются суммарными длинами соответствующих отрезков, составляющих . А в случае пространства вероятности оцениваются через суммарные объемы соответствующих областей, составляющих .

8.Пример задачи на геометрическую вероятность.

Задача 8.1.

Мария и Иван хотят встретиться в промежутке времени от 0 до 1 часа пополудни. Они люди безалаберные и каждый из них появится на месте встречи в свой случайный момент времени или соответственно из отрезка . Они условились, что каждый пришедший ждет своего товарища в течение 15 минут или до момента времени t=1, если от момента прихода до момента времени t=1 остается меньше 15 минут.

Какова вероятность, что Мария и Иван встретятся?

Решение:

Сделаем следующее построение. Введем прямоугольную систему координат X0Y. Полагаем х=, y=. Тогда точка с координатами х и у соответствует приходу Марии в момент х= и приходу Ивана в момент y=. Достоверному событию соответствует на плоскости ХОУ квадрат : Событию А, которое осуществляется тогда и только тогда, когда Мария и Иван встретятся соответствует область , которая состоит из точек, лежащих в квадрате и к тому же удовлетворяющих условию , т.е. : См. фиг.8.1.

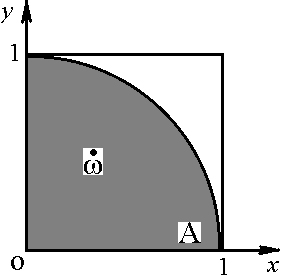
Фиг.8.1.

По формуле (7.1) получаем

Р(А)=S/S=1–2∙(1/2)∙(3/4)=1–9/16=7/16(8.1)

Ответ: Вероятность встречи Марии и Ивана равна 7/16.

9.Случайные величины.

Очень важным в теории вероятностей является понятие случайной величины x. Это величина, для которой тот факт, что она принимает то или иное значение, является случайным событием. Например, когда компьютеру на одной из версий языка Pascal, дается команда x=random(1000)/1000, то компьютер выдает случайным образом значение случайной величины х, 0≤x≤1. При этом вероятность Р(A) события A={α≤x≤β, 0≤α≤β≤1} определяется равенством

Р(А)=Р(α≤x≤β)=β–α (9.1)

Иначе говоря, здесь как раз вероятность того, что случайная величина х принимает то или иное значение в пределах отрезка {α≤x≤β,0≤α≤β≤1}, определяется геометрически через длину этого отрезка.

Рассмотрим случайную величину х, которая может принять конечное число n различных значений с вероятностями РР.

Например, если мы бросаем один раз игральную кость, то случайной величиной х будет выпавшее количество очков, т.е.k=6,, РРР.

10.Математическое ожидание.

Математическим ожиданием E(x) для случайной величины x, которая может принимать значения x и только такие значения с вероятностями Р(x)=Р, называют число, которое определяется равенством

i=k i=k

E(x)=∑xi·Рi, ∑ Рi=1, Рi≥0, i=1,…,k(10.1)

i=1 i=1

Например, в случае с игральной костью математическое ожидание количества очков x, которое выпадет, будет согласно (10.1) числом

E(x)=(1/6)∙(1+2+3+4+5+6)=(1/6)∙21=7/2=(10.2)

Смысл понятия математического ожидания раскрывается в законе больших чисел. Этот закон проявляется следующим образом. Если сделать подряд очень большое число n независимых испытаний при одинаковых условиях, и таких, что каждый раз осуществляется одно из значений рассматриваемой случайной величины х, то с вероятностью очень близкой к единице, то есть практически наверняка и с большой степенью точности будет выполняться приближенное равенство

(x(1)+x(2)+…+x(n))/n ≈ E(x)(10.3)

Здесь x(i)–значение случайной величины x, которое появляется в i-том испытании. Закон больших чисел обоснован теоретически при определенных аксиомах теории вероятностей и многократно подтвержден на практике.

Пусть некоторая случайная величина х* является суммой случайных величин

(10.4)

тогда математическое ожидание E(x*) равно сумме математических ожиданий Е(х)

(10.5) 11.Дисперсия случайной величины.

Дисперсией D(x) случайной величины х называют число, которое определяется по формуле

D(x)=E(x–E(x))(11.1)

Поэтому дисперсия D(x) случайной величины х, которая может принимать значения с вероятностями Р,…Ропределяется, как число i=k i=k j=k

D(x)=∑(x–E(x))∙P=∑(x–)∙P (11.2)

i=1 i=1 j=1

Например, в случае с игральной костью для дисперсии D(x) получаем следующее число

D(x)==(1/6)∙((1-7/2)+(2-7/2)+(3-7/2)+(4-7/2)+(5-7/2)+(6-7/2))=(1/6)∙(25/4+9/4+1/4+1/4+9/4+25/4)=(1/6)∙(35/2)=35/12(11.3)

Пусть некоторая случайная величина х* является суммой (10.4) случайных величин . Пусть эти случайные величины независимы. Это означает, что вероятность, с которой может осуществиться то или иное значение случайной величины не зависит от того, какое значение принимают другие случайные величины . Тогда доказывается, что дисперсия случайной величины х* является суммой дисперсии случайных величин

(11.4)

Важно заметить, что если случайные величины не являются независимыми, то дисперсия их суммы не обязательно равна сумме их дисперсий.

12.Закон больших чисел.

В этом разделе приведу аккуратную формулировку закона больших чисел, которая восходит к замечательному математику нашей страны П.Л.Чебышеву. Пусть имеем некоторую случайную величину х. Выберем какое-нибудь положительное число М. Отберем те значения случайной величины х, для которых выполняется условие

(12.1)

Из выражения для дисперсии (11.2) и из неравенства (12.1) вытекает следующее неравенство

РРР (12.2)

Здесь суммирование в (12.2) выполняется по тем индексам j, для которых выполнено неравенство.

Предположим теперь, что произведено n независимых испытаний. Пусть в i-том испытании осуществляется значение случайной величины . Пусть математические ожидания и дисперсии всех этих независимых случайных величин одинаковы. Тогда согласно материалу из разделов 10,11 для суммы

(12.3)

этих случайных величин и из (12.2) получаем следующее неравенство

Р

·Р (12.4)

Так как случайные величины независимы, то дисперсия их суммы равна сумме их дисперсий. Кроме того, все дисперсии равны друг другу и все математические ожидания тоже равны друг другу . Поэтому из (12.4) получаем неравенство

Р(12.5)

Введем число ε=M/n. Тогда из (12.5) получаем неравенство

Р(12.6)

Отсюда для противоположного события

(12.7)

из (12.6) получаем следующее неравенство П.Л.Чебышева

Р(12.8)

Таким образом, из (12.8) получается закон больших чисел П.Л.Чебышева:

Для любого сколь угодно малого положительного числа ε и числа β<1 найдется такое число N, что при числе испытаний n>N, будет справедливо неравенство

(12.9)

В самом деле, согласно (12.8) достаточно выбрать в качестве числа N наименьшее из натуральных чисел, удовлетворяющих неравенству , то есть

(12.10)

Это означает следующее. Какие бы числа и мы ни выбрали, если сделать количество n независимых испытаний больше, чем число N, то среднее значение случайной величины будет отличаться от математического ожидания меньше, чем на ε с вероятностью большей, чем β. Иначе говоря, при неограниченном увеличении числа независимых испытаний среднее значение случайной величины стремится к математическому ожиданию Е с вероятностью, приближающейся к единице.

13.Испытания по схеме Бернулли.

Так называется следующая серия независимых испытаний. Пусть производится n испытаний. В i-том испытании может осуществиться случайное событие Ai с вероятностью Рi,i=1,…,n. Все события Аi независимы в совокупности. То есть вероятность события Аi не зависит от того, осуществляются или нет события Аj,j=1,…,n, ji. Рассмотрим здесь такой частный случай, когда все вероятности Рi равны друг другу и равны ,0‹‹1. То есть

Р(Аi)=, P(Ai*)=q, q=1-, 0‹‹1, 0‹q‹1, i=1,…,n(13.1)

Например, пусть испытания состоят в том, что случайная точка в i-том испытании обязательно появляется в квадрате со стороной равной единице. Событие Аi состоит в том, что точка оказывается в четверти круга, вписанного в квадрат и имеющего радиус равный единице (см.раздел7). Согласно (7.2) имеем

Р(Ai)==(13.2)

Справедливо следующее утверждение.

Теорема Бернулли: Пусть производится n испытаний по схеме Бернулли. Пусть события Аi осуществились в m испытаниях.

Для любых чисел и найдется такое натуральное число N, что при числе испытаний n>N будет справедливо неравенство

P(|m/n–|<)>(13.3)

В самом деле, свяжем с i-тым испытанием случайную величину . Пусть эта величина принимает значение равное единице, если осуществляется событие Аi, и принимает значение равное нулю, если событие Аi не осуществляется, т.е. осуществляется противоположное событие Аi*. Вычислим математическое ожидание Еi и дисперсию Di случайной величины . Имеем

pq=(13.4)

pppqq∙+p∙q=∙q∙(q+)=∙q∙1=∙q(13.5)

Так как в нашем случае

(13.6)

то из закона больших чисел (12.9),(12.10) получаем неравенство (13.3), если только

(13.7)

Это и доказывает теорему Бернулли.

Например, если мы хотим проверить теорему Бернулли на примере вычисления числа π с точностью до с вероятностью большей, чем , то нам надо сделать испытания по схеме Бернулли в соответствии с разделом 7, т.е. получить согласно текущему разделу неравенство

P(|m/n–π/4|<0.01)>0.99(13.8)

Для этого согласно (13.7) достаточно выбрать число

(13.9)

с большим запасом.

Такое испытание было сделано на компьютере по программе, приведенной в следующем разделе. Получилось

4∙m/n=3.1424 (13.10)

Мы знаем, что число π=3.1415925626…. То есть действительно получилось число с точностью по крайней мере до 0.01.

14.Программа в