Скачать

Моделювання економіки

МІНІСТЕРСТВО НАУКИ І ОСВІТИ УКРАЇНИ

ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ

До друку і в світ дозволяю

Перший проректор

______________В.В.Семенець

"____"__________2004р.

Методичні вказівки

до виконання курсового проекту з ДИСЦИПЛІНИ

"Моделювання економіки"

для студентів усіх форм навчання

спеціальності "Економічна кібернетика"

П.С.Ковтун

Б.П.Косіковська

поз. 4

Харків 2004

Міністерство освіти і науки України

Харківський Національний університет радіоелектроніки

Методичні вказівки

до виконання курсового проекту з ДИСЦИПЛІНИ

"Моделювання економіки"

для студентів усіх форм навчання

спеціальності "Економічна кібернетика"

Затверджено

кафедрою “Економічна кібернетика”

Протокол № 2 від 14.09.04

Харків 2005

Методичні вказівки до виконання курсового проекту з дисципліни "Моделювання економіки" для студентів усіх форм навчання спеціальності "Економічна кібернетика" / Упоряд. Н.Б. Івченко. – Харків: ХНУРЕ, 2005- 28с.

Упорядник Н. Б. Івченко

ЗМІСТ

Вступ ...............................................................................................................5

1 Задачі курсового проектування………………............................................5

2 Тематика курсових проектів......................................................................5

3 Структура та зміст курсового проекту.......................................................6

4 Методичні вказівки до виконання курсового проекту

"Дослідження глобальних моделей виробництва та споживання"................6

4.1 Побудова та опис двогалузевої макроекономічної моделі......................7

4.2 Дослідження виробничих функцій........................................................8

4.3 Дослідження моделі "витрати-випуск" Леонтьєва................................1

4.4 Дослідження моделей міжгалузевих балансів.......................................14

4.5 Дослідження моделі Неймана..............................................................16

4.6 Дослідження моделі Солоу...................................................................18

4.7 Побудова схеми алгоритму...................................................................21

4.8 Опис програми......................................................................................21

4.9 Інструкція користувачу програми.........................................................22

5 Початкові дані..........................................................................................22

6 Вимоги до оформлення курсового проекту.............................................22

7 Організація проектування та захист проекту...........................................24

Рекомендована література.....................................................................................25 Додаток А Завдання до курсового проекту.......................................................26

Додаток Б Зразок титульного аркуша..........................................................27

ВСТУП

Даний курсовий проект виконується з дисципліни "Моделювання економіки". Це дисципліна є одним з головних курсів у процесі підготовки сучасних фахівців з економічноі кібернетики. Курс має одночасно теоретичне, методологічне та прикладне значення.

Для виконання курсового проекту необхідні знання з економіки, матричної алгебри, лінійного програмування. Робота над курсовим проектом передбачає творчий підхід до розв’язання задач.

1 ЗАДАЧІ КУРСОВОГО ПРОЕКТУВАННЯ

Метою курсового проектування є закріплення теоретичних знань про типові економіко-математичні моделі, набуття навичок практичної роботи з ними, програмна реалізація цих моделей. В умовах ринкової економіки використання типових та розробка нових моделей дає змогу правильно оцінити та передбачити різні економічні показники, прийняти оптимальні управлінські рішення. Використання комп'ютерів дозволяє розв'язувати задачі великих розмірів. В курсовій роботі студенти виконують конкретні розрахунки, які необхідні для дослідження типових економіко-математичних моделей.

2 ТЕМАТИКА КУРСОВИХ ПРОЕКТІВ

До виконання пропонуються такі темі курсових проектів:

1. Споживач та його поведінка.

2. Виробник та його поведінка.

3. Моделі економічної взаємодії на простих ринках.

4. Співробітництво та конкуренція двох фірм на ринку одного товару.

5. Моделі ринків.

6. Моделі міжгалузевих зв’язків.

7. Моделі аналізу макроекономічної політики.

8. Дослідження глобальних моделей виробництва та споживання.

Теми 1 - 7 носять реферативний характер. Але вони також вимагають розробки програми за однією із моделей. Розробка програми супроводжується побудовою схеми алгоритму, описом програми та підготовкою інструкції для користувача програми.

За згодою із керівником курсового проекту окремі студенти можуть виконувати роботи, які використовуються в учбовому процесі (лабораторні роботи, ділові ігри тощо).

3 СТРУКТУРА ТА ЗМІСТ КУРСОВОГО ПРОЕКТУ

Курсовий проект описується в пояснювальній записці. У пояснювальній записці мають бути:

Завдання до курсового проекту

ЗМІСТ

Вступ

1 Теоретично-розрахункова частина

2 Програмна реалізація моделі

висновки

Перелік посилань

додаток а Лістінг програми

У вступі розглядається актуальність теми. Теоретично-розрахункова частина містить опис моделей, розрахунки, табличний та графічний матеріали. Розділ “Програмна реалізація моделі” містить побудову схеми алгоритму, опис програми та інструкцію користувачу програми. У висновках підводяться підсумки зробленої роботи, приводяться висновки.

4 МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ КУРСОВОГО ПРОЕКТУ “ДОСЛІДЖЕННЯ ГЛОБАЛЬНИХ МОДЕЛЕЙ ВИРОБНИЦТВА ТА СПОЖИВАННЯ”

В даному курсовому проекті необхідно розглянути декілька глобальних моделей виробництва та споживання.

Розділ “1 Теоретично-розрахункова частина” вміщує підрозділи:

1.1 Побудова та опис двогалузевої макроекономічної моделі

1.2 Дослідження виробничих функцій

1.3 Дослідження моделі "витрати-випуск" Леонтьєва

1.4 Дослідження моделей міжгалузевих зв’язків

1.5 Дослідження моделі Неймана.

1.6 Дослідження моделі Солоу

У розділі “2 Програмна реалізація моделі” розглядаються підрозділи:

2.1 Побудова схеми алгоритму

2.2 Опис програми

2.3 Інструкція користувачу програми

Для здійснення конкретних розрахунків необхідно користуватись початковими даними заданого варіанту.

4.1 Побудова та опис двогалузевої макроекономічної моделі

Розглянемо модель галузі економіки, що є декомпозицією загальної вербальної моделі. Нехай галузь випускає продукцію тільки одного виду. На рис. 4.1. показана схема галузі економіки. Схема включає підсистему виробництва продукції F, блоки розподілення R_X, R_Y, R_I, блок основних виробничих фондів К' та блок V приросту капіталу.

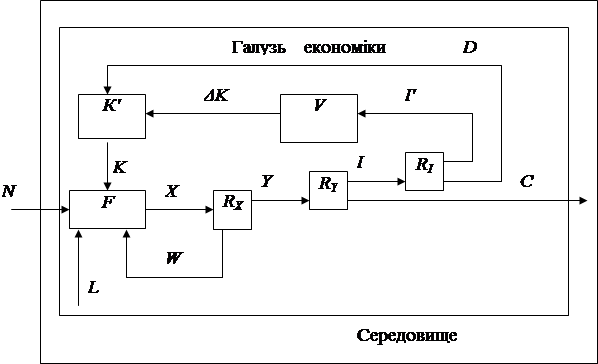
Рисунок 4.1 – Схема галузі економіки

Галузь характеризують такі фактори:

К – основні виробничі фонди або виробничий капітал;

N – природні ресурси;

L – трудові ресурси;

X – валова продукція;

Y – кінцева продукція;

W – проміжна продукція;

I – інвестиції;

C – продукція невиробничого споживання;

I' – чисті інвестиції, які йдуть на розширення основних виробничих фондів;

D – амортизаційні відрахування;

ΔK – приріст виробничого капіталу.

На вхід підсистеми F надходять основні виробничі фактори К, природні ресурси N, трудові ресурси L, проміжна продукція W. Ця продукція у блоці R_x розподіляється на кінцеву продукцію Y та проміжну продукцію W, яка йде на виробниче споживання

X=W+Y.

У блоці R_Yпродукція Y розподіляється на інвестиції I та продукцію невиробничого споживання С

Y=I+C.

У блоці R_I інвестиції I поділяються на амортизаційні відрахування D та чисті інвестиції I' , які йдуть до блоку V на розширення ОВФ.

На підставі цієї моделі побудувати двогалузеву макроекономічну модель та дати її опис. Схему кожної галузі необхідно ідентифікувати та доповнити блоком розподілення R_Wi,. У цьому блоці проміжна продукція W_i,, розподіляється на проміжну продукцію, яка використовується в своїй та іншій галузях (та W₁₂W₁₁- для першої галузі, W₂₂та W₂₁- для другої галузі). Чисті інвестиції I'_i, , також поділяються на чисті інвестиції, які використовуються в своїй та іншій галузях (I'₁₁та I'₁₂ - для першої галузі, I'₂₂ та I'₂₁ - для другої галузі). Міжгалузевими потоками тут будуть W₁₂, W₂₁, I'_12., I'₂₁.Записати математичні вирази для X_i, Y_i, I_i, .

4.2 Дослідження виробничих функцій

Підсистему виробництва продукції F (рис. 4.1) можна описати за допомогою виробничої функції

X=F(K, L).

Тут змінні характеризують такі фактори: K - обсяг виробничих фондів у вартісному або натуральному вигляді (вартість або кількість обладнання), L - обсяг трудових ресурсів (кількість робітників, кількість людино-днів) , X - обсяг продукції (валової) у вартісному або натуральному вигляді.

У даному підрозділі розглядаються виробнича функція Кобба-Дугласа (для першої галузі) та лінійна виробнича функція (для другої галузі). Припускається, що ці функції неперервні та диференційовані.

Виробнича функція Кобба-Дугласа ( CDPF ) належить до найбільш відомих, широко використовуваних функцій. Функція має вигляд

X₁=aK₁^αL₁^1-α,

(a,α,(1-α))>0, α<1,

де (a,α) - параметри моделі.

Параметр a залежить від одиниць вимірювання змінних.

Для функції Кобба-Дугласа виконуються такі вимоги

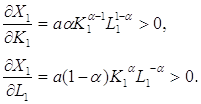
Перша похідна характеризує граничну фондовіддачу. Із виразу видно, що для цієї функції гранична фондовіддача пропорційна середній фондовіддачі та менше її

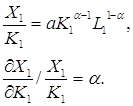
Аналогічно визначається середня та гранична продуктивності праці. Для них також виконується відношення: гранична продуктивність праці пропорційна середній продуктивності та менше її. Знайдемо тепер еластичність продукції за основними фондами

,

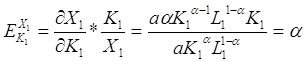та еластичність продукції за трудовими ресурсами

.

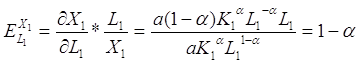Еластичність показує, як зміниться величина Х₁, якщо величина К₁або L₁зміниться на 1%.

Знайдемо також граничні норми заміщення основних фондів трудовими ресурсами

,

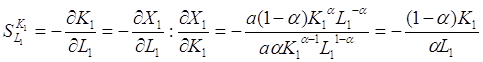та трудових ресурсів основними фондами

.

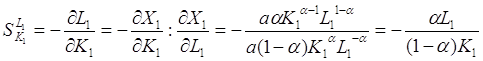Ці норми показують, як при незмінній величині продукції можна змінити співвідношення між факторами.

За значеннями a та α заданого варіанту побудувати виробничу функцію Кобба-Дугласа для першої галузі та визначити основні характеристики:

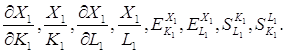
Доказати однорідність першого степеня виробничої функції Кобба-Дугласа.

Для другої галузі необхідно розглянути лінійну виробничу функцію

C₂=b₁K₂+b₂L₂,

b₁=10i, b₂=і,

де і- номер заданого варіанту. Дослідити цю функцію, для цього обчислити характеристики

, , , , .

Доказати однорідність першого степеня лінійної виробничої функції.

4.3 Дослідження моделі "витрати-випуск" Леонтьєва

В моделі Леонтьєва діють підсистема виробництва продукції F та блок розподілу R_X, змінні X,Y,W (рис. 4.1).

Якщо позначити через X_i- валову продукцію і-ї галузі, Y_i - кінцеву продукцію і-ї галузі, W_i – проміжну продукцію і-ї галузі, то можна записати,

X_i-W_i=Yі, .

Тут - кількість галузей. В цій моделі діє припущення, що в кожній галузі виробництво здійснюється одним технологічним способом або галузі випускають однорідну продукцію. Нехай проміжна продукція і-ї галузі дорівнює

,

де X_j - валова продукція j-ї галузі, , А_ij- кількість продукції і-ї галузі, яка витрачається на виробництво одиниці продукції j- ї галузі.

Модель Леонтьєва характеризується виробничою матрицею А

A=(A_ij), ; .

Ця матриця також називається матрицею коефіцієнтів прямих матеріальних витрат.

В матрично-векторній формі модель має вигляд

(I-A)=,

де I – одинична матриця розміром (n×n),

- вектор валової продукції (вектор випуску),

- вектор кінцевої продукції.

Вектор валової продукції можна знайти за формулою

=(I-A)^-1,

G=(I-A)^-1,

=G,

де G - обернена матриця Леонтьєва або мультиплікатор Леонтьєва . Матриця G дорівнює

G=(G_ij), , .

Ця матриця називається матрицею коефіцієнтів повних матеріальних витрат. Елемент G_ijпоказує потребу в валовій продукції і-ї галузі для виробництва одиниці кінцевої продукції j -ї галузі.

Задача планування випуску валової продукції є перетворенням вектора кінцевої продукції за допомогою матриці (I-A)^-1 у вихідний вектор валової продукції

=(I-A)^-1.

Виникає питання відносно умов, за яких існує така матриця (I-A)^-1 , що для будь-якого невід'ємного вектора ,≥0, вектор (I-A)^-1 також невід'ємний. Матриця А в такому разі називається невід'ємною, якщо всі її елементи є невід'ємними. Для економічних систем матриця А завжди невід'ємна.

Умови продуктивності матриці А зв'язані з використанням одного з тверджень:

1) максимальне власне число λ(A) матриці А менше 1;

2) матриця (I-A) має невід'ємну обернену матрицю;

3) матричний ряд

I+A+A²+...+A^r+… = ,

A⁰=I,

(так званий ряд Неймана матриці А) збігається, при цьому його сума дорівнює оберненій матриці (I-A)^-1

=(I-A)^-1,

4) послідовні головні мінори матриці (I-A) додатні.

За даними А та побудувати модель Леонтьєва для двох галузей та знайти вектор валової продукції .

Для цього виконати такі дії:

1) знайти матрицю (I-A), де І – одинична матриця

I=,

2) обчислити визначник матриці |I-A|.

Для обчислення визначника можна скористатись правилом трикутника. Наприклад, для матриці В

В=,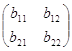

визначник дорівнює:

,

3) знайти мінори для елементів матриці (I-A). Нагадаємо визначення мінору. Мінором M_ik називається визначник (n-1) порядку, який одержуємо після викреслення і - рядка та k- стовпця, ; . Наприклад, мінор М₁₁ дорівнює.

;

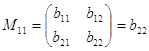4) знайти алгебраїчні доповнення для елементів матриці (I-A).

Позначимо алгебраїчне доповнення ,; . Алгебраїчним доповненням називається мінор, який береться зі знаком (-1)^i+k