Скачать

Моделирование макроэкономических процессов

Макроэкономическая теория объясняет, откуда возникают общие экономические проблемы, как они развиваются и как их можно решить. Главным методом для этого служат макроэкономические модели.

В экономике одновременно действуют многочисленные макроэкономические процессы, они действуют часто в противоположных направлениях. Очень трудно охватить и понять всё это многообразие экономических явлений и процессов, тем более установить зависимости между ними. Для этого используется моделирование макроэкономических процессов, то есть построение макроэкономических моделей. При этом приходится отвлекаться, абстрагироваться, от многих несущественных экономических явлений и процессов. В модели отражается определённая зависимость между макроэкономическими переменными, другими словами формулируется макроэкономическая закономерность.

Макроэкономическая модель в упрощённой форме представляет важнейшие особенности и наиболее существенные черты исследуемых макроэкономических процессов, формулирует важнейшие зависимости между ними.

Необходимо заметить, что макроэкономическая модель может быть представлена не только в математической форме. Модели формулируются разными способами: математическое описание с помощью уравнений, неравенств, графическое изображение, описание с помощью таблицы, словесная формулировка. В дальнейшем нам представится возможность продемонстрировать это при анализе макроэкономических закономерностей развития рыночной экономики.

Примером макроэкономической зависимости может служить важнейшая зависимость между изменением масштабов национального производства (уровнем ВВП), нормой безработицы и инфляцией, действующая в развитой рыночной экономике. В условиях экономического спада, когда ВВП сокращается, норма безработицы увеличивается, темпы инфляции снижаются. Другим примером макроэкономической зависимости может служить зависимость между денежной массой в обращении и уровнем цен. При прочих равных условиях увеличение денежной массы ведёт к росту цен, увеличению темпов инфляции.

Цель данной работы, рассмотреть модели макроэкономических процессов, их разнообразие, выделить особенности каждой при решении экономических задач и обозначить границы их применения и рассмотреть эти примеры на производстве и управлении предприятии.

Актуальность темы курсовой работы, объясняется тем, что если развитие эконометрического анализа привело к использованию моделей на микроэкономическом уровне, то своего бурного расцвета моделирование достигло в применении к макроэкономике, так что модели стали одним из важнейших инструментов прогнозирования и изучения экономической политики. Эволюция техники среднесрочного и краткосрочного прогнозирования произошла под знаком моделирования, которое позволило математи­чески формализовать процесс прогнозирования и использовать при этом практические возможности компьютерного программирования. Таким образом, макроэкономическая модель является упрощенной схемой движения экономики на протяжении определенного периода, схемой, отражающей взаимосвязи множества экономических и финансовых переменных.

Задачи курсовой работы: раскрыть особенность каждой макроэкономической модели.

1. ТЕОРЕТИКО-МЕТОДИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИРОВАНИЯ МАКРОЭКОНОМИЧЕСКИХ ПРОЦЕССОВ И СИСТЕМ

1.1 МОДЕЛЬ ХАРРРОДА - ДОМАРА, КАК ПРИМЕР МОДЕЛИ МАКРОЭКОНОМИЧЕСКОЙ ДИНАМИКИ

Модель описывает динамику дохода Y(t), который рассматривается как сумма потребления C(t) и инвестиций I(t). Экономика считается закрытой, поэтому чистый эк­спорт равен нулю, а государственные расходы в модели не выделя­ются. Основная предпосылка модели роста - формула взаимосвязи между инвестициями и скоростью роста дохода. Предполагается, что скорость роста дохода пропорциональна инвестициям:

I(t) =B,

где В - коэффициент капиталоемкости прироста дохода, или приростной капиталоемкости (соответственно, обратная ему величина — называется приростной капиталоотдачей). Тем самым в модель фактически включаются следующие предпосылки:

· инвестиционный лаг равен нулю: инвестиции мгновенно переходят в прирост капитала. Формально это означает, что ∆ K(t) =I(t), где ∆K(t) - непрерывная функция прироста капитала во времени;

· выбытие капитала отсутствует;

· производственная функция в модели линейна; это вытекает из пропорциональности прироста дохода приросту капитала:

dY(t) =

Линейная производственная функция Y(t)= α L(t) + b K(t)+c

Где , обладает этим свойством в том случае, если либо α=0, либо L(t)=const. . Тем самым следующая предпосылка такова:

· затраты труда постоянны во времени либо выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом;

· модель не учитывает технического прогресса.

Перечисленные предпосылки, конечно, существенно огрубляют описание динамики реальных макроэкономических процессов, делают затруднительным применение данной модели, например, для непосредственного расчета или прогноза величины совокупного выпуска или дохода. Однако данная модель и не предназначена для этого; в то же время ее относительная простота позволяет более глубоко изучить взаимосвязь динамики инвестиций и роста выпуска, получить точные формулы траекторий рассматриваемых параметров при сделанных предпосылках.

Зависимость, связывающая между собой во времени показатели инвестиций, определяемый ими объем основного капитала и уровень выпуска (дохода), является базовой во всех моделях макроэкономической динамики. Кроме того, в этих моделях необходимо определить принципы формирования структуры выпуска (дохода), распределения его между составляющими, прежде всего - между потреблением и накоплением. Эти принципы могут основываться на оптимизационном подходе (обычно это максимизация совокупных объемов потребления в той или иной форме), экстраполяционном, равновесном и других. В рассматриваемой модели предполага­ется, что динамика объема потребления С(t) задается экзогенно. Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом или иметь какую-либо другую динамику (в первых двух случаях более просто получить решение модели).

Простейший вариант модели получается, если считать С(t) = 0. Этот случай совершенно нереалистичен с практической точки зре­ния, однако в нем все ресурсы направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста. В этом случае получаем:

Это – линейное однородное дифференциальное уравнение, и его решение имеет вид

Y(t) =Y(0)·е

(что легко проверить дифференцированием). Непрерывный темп прироста здесь равен. Это максимально возможный (технологический) темп прироста.

Пусть теперь C(t) =С постоянного времени. Получаем неоднородное линейное дифференциальное уравнение Y(t)= BY(t)+C. Его частым решение являются Y(t)=С, и складывая его с общим решение однородного уравнения

Y(t)=A·е, получаем его общее решение

Y(t) = A·е+ C,

откуда, подставив t = 0, имеем

А = Y(0)-C = I(0) и Y(t) = (Y(0) –C)·е+ C.

Непрерывный темп прироста дохода y(t) = в этом решении равен y(t)=(1-). Он составляет (1-) в начальный момент времени (при t = 0) и, возрастая, стремиться к при t → ∞ (что понятно, поскольку доход растет, а постоянный объем потребления составляет все меньшую его долю). Величина в скобках α(t) =(1- ) есть норма накопления в момент времени t, и темп прироста дохода оказывается пропорциональным этой величине, как и показателю приростной капиталоотдачи .

Итак, при прочих равных рост нормы накопления пропорционально увеличивает темпы прироста дохода. В то же время это снижает уровень текущего потребления, и для разрешения проблемы согласования конкурентных целей увеличения темпов роста и уровня текущего благосостояния в модель обычно включают элементы оптимизации. В этом случае решается оптимизационная задача на максимум общего объема потребления за конечный или бесконечный период времени. Для отражения предпочтительности более раннего получения результата в модель включается временное дисконтирование, при котором более ранний результат учитывается в критерии с большим "весом".

Наконец, рассмотрим вариант модели с показателем потребления С(t), растущим с постоянным темпом r. С(t) = С(0) е. Дифференциальное уравнение этой модели имеет вид Y(t)=BY(t)+C(0)·е. Решение этого уравнения (проверьте дифференцированием) таково:

Y(t)=(Y(0) -)·е+()·е

Из общих соображений ясно, что темп прироста потребления г не должен быть больше максимально возможного общего темпа

прироста так как иначе потребление будет занимать все большую и в конце концов – подавляющую часть дохода, что сведет к нулю сначала инвестиции, а затем и доход. Ясно это и из формулы решения модели.

В решении рассматриваемой модели роста при r < многое зависит от соотношения между r и ρ=( в числители стоит =1- - норма накопления в начальный момент времени). Если r = ρ, то темп прироста дохода равен темпу прироста потребления, и решением является Y(t) =Н(0)·е. Норма накопления α(t) в этом случае постоянно во времени и равна , а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоемкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.

Таким образом, если требуется поддерживать постоянный темп прироста потребления r, не превышающий технологического темпа, то для максимизации объема потребления за любой период нужно установить начальную норму накопления = Br.. Более сложен вопрос о том, какой уровень темпа r-более предпочтителен. Большая его величина позволяет обеспечить больший объем потребления за длительный период, но это происходит за счет сокращения потребления на начальном этапе. Таким образом, для выбора значения r-(если оно предполагается постоянным) нужна информация о межвременных предпочтениях лица, принимающего решение.

1.2 МОДЕЛЬ СОЛОУ, КАК ПРИМЕР МАКРОЭКОНОМИЧЕСКОЙ ДИНАМИКИ

Другой тип модели экономического роста представляет модель, предложенная лауреатом Нобелевской премии Р.Солоу. По сравнению с уже рассмотренной моделью роста модель Солоу позволяет более точно описать некоторые особенности макроэкономических процессов. Во-первых, производственная функция в этой модели нелинейна и обладает свойством убывания предельной производительности. Во-вторых, модель учитывает выбытие основного капитала. В-третьих, в модель Солоу включается описание динамики трудовых ресурсов и технического прогресса и их влияние на экономический рост. В-четвертых, здесь ставится и решается задача максимизации уровня потребления на некотором множестве устойчивых траекторий. Все это, конечно, усложняет структуру модели, и получение точных формул для траекторий изменения основных ее показателей становится существенно более сложной задачей. По­этому некоторые другие аспекты описываются в базовой модели Солоу упрощенно: например, считаются постоянными норма сбере­жений и норма выбытия капитала, инвестиционные лаги отсутствуют, а производственная функция имеет постоянную отдачу от масштаба. Кроме того, на начальном уровне анализа модели ищутся не траектории изменения всех ее показателей (как в модели Харрода-Домара), а характеристики состояний устойчивого равновесия, к которым система выходит в долгосрочном периоде. С формальной точки зрения это представляет собой существенно более простую задачу.

Мы не ставим здесь задачу подробно излагать модель Солоу, сформулируем лишь основные ее предпосылки, обозначения и вы­воды.

Предпосылки и обозначения модели Солоу:

· Производственная функция имеет вид Y= F(K,L) (Y – выпуск или доход, К- капитал, L – труд). Отдача от масштаба постоянна :

F(zK, zL) = zF(K,L). Предельная производительность факторов положительна, но убывает:

Y>0; Y>0; Y<0 ; Y<0 ;

· Величина выбытия капитала W пропорциональна его величине K: W=δ·K,

где δ – норма выбытия;

· норма сбережений (инвестиций) α постоянна, и инвестиции I равны α Y;

· доход Y распределяется на потребление и инвестиции Y=C+1

· численность занятых L растет с постоянным темпом n;

· трудосберегающий технический прогресс имеет темп g , то есть число единиц труда с постоянной эффективностью в расчете на одного работающего растет с темпом g

При сделанных предпосылках производственную функцию можно

рассматривать как зависимость производительности труда от

его капиталовооруженности :y =F(k) (здесь L- число единиц труда с постоянной эффективностью (то есть численность занятых при отсутствии трудосберегающего технического прогресса, либо численность условных работников с одинаковой эффективностью - при его наличии). Это вытекает из того, что Y=F(K,L) =L·F(.

Инвестиции приводят к росту капиталовооруженности, а выбытие капитала, рост численности работающих и числа единиц труда с постоянной эффективностью - к ее снижению. Прирост капиталовооруженности k. в результате инвестиций равен i = . Темп снижения капиталовооруженности за счет остальных факторов равен (δ+n+g) (в точности равен, если У,К,L - непрерывные функции времени, и приближенно равен в дискретном случае при малых δ+n+g). Величина снижения капиталовооруженности за счет этих фак­торов равна (δ+n+g)k.

Величина k находится в состоянии устойчивого равновесия, если ее прирост за счет инвестиций равен ее уменьшению за счет других факторов. Поскольку Y=С+I, после деления этого тождества на L имеем y= c+I , где у - доход, с - потребление, а i - инвестиции на одну единицу труда с постоянной эффективностью. Следовательно, величина I равна α f(k). Условие стабильности показателя k,, таким образом, записывается как

(δ+n+g)·k* =α·f(k*)

и величина k* называется устойчивым уровнем капиталовооруженности. На рис. 1 показана устойчивость равновесия при k = k*. Это - точка равновесия для показателя k, поскольку в этой точке величина удельного прироста капиталовооруженности равна величине ее удельного сокращения, и показатель k остается неизменным. Это равновесие устойчиво, поскольку при k< k* , наоборот, удельные инвестиции ниже, чем уменьшение капиталовооруженности, и ее величина падает, пока не достигнет k*. Из рис. 1 можно видеть, что в случае увеличения нормы сбережения а график функции инвестиций пойдет выше и, следовательно пересечет прямую (δ+n+g)k правее. Итак, рост нормы сбережения приводит к увеличению устойчивого уровня капиталовооруженности k*, а, следовательно, и устойчивого уровня дохода на единицу труда y* = f(k*)

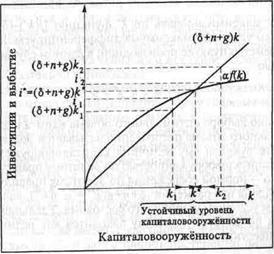
Рис.1

Если численность работающих не растет (или растет медленнее), то есть показатель n равен нулю (или меньше по величине), то прямая (δ+n+g) k имеет меньший наклон и точка k* сдвигается вправо. То же самое происходит при более низком (или нулевом) темпе трудосберегающего технического прогресса g.В устойчивом состоянии темп прироста показателей k,y,c,i равен нулю. Поскольку все это - удельные показатели в расчете на единицу труда с постоянной эффективностью, а эффективность труда одного занятого растет с темпом g, показатели капитала, дохода, потребления и инвестиций в расчете на одного занятого растут с темпом g. При росте численности занятых с темпом n общий объем капитала, дохода, потребления и инвестиций растет в устойчивом состоянии с темпом (n+g). Следовательно, модель Солоу показывает, что единственным источником длительного, устойчивого роста дохода на одного работника, а, следовательно, и душевого потребления, является технический прогресс.

1.3 МОДЕЛЬ МАКРОЭКОНОМИЧЕСКОГО РАВНОВЕСИЯ: ОБЩАЯ МОДЕЛЬ СОВОКУПНОГО СПРОСА – СОВОКУПНОГО ПРЕДЛОЖЕНИЯ

В условиях рыночной экономики центральным звеном экономического механизма является конкурентное ценообразование. В этом механизме действуют две важнейшие стороны - спрос и предложение.

Совокупный спрос (AD) - это объём товаров и услуг в экономике в целом, который потребители, предприятия и правительство готовы купить при определённом уровне цен, другими словами, это величина запланированных расходов на товары и услуги в экономике в целом при данном уровне цен.

важнейшими частями совокупного спроса являются: потребительские расходы домашних хозяйств (С), инвестиционные расходы предприятий (I), государственные расходы (G), расходы иностранцев, или чистый экспорт (NX).

AD = C + I + G + NX

Совокупный спрос и его величина могут быть изображены графически с помощью кривой совокупного спроса. Если мы по вертикали отметим уровень цен (Р), а по горизонтали - выпуск продукции (Y), то есть ВВП, то, принимая различные значения уровня цен и выпуска, можно построить кривую совокупного спроса AD.

Второй определяющей частью в модели AD-AS является совокупное предложение. Также как и в случае с совокупным спросом мы определим сущность совокупного предложения, факторы, влияющие на его величину.

Совокупное предложение - это объём товаров и услуг, производимых в экономике в целом в данном году и предложенных предприятиями на рынке населению, государству и друг другу при данном уровне цен.

Совокупное предложение и его величина могут быть изображены графически с помощью кривой совокупного предложения. Если мы по вертикали отметим уровень цен (Р), а по горизонтали - выпуск продукции (Y), то есть ВВП, то, принимая различные значения уровня цен и выпуска, можно построить кривую совокупного предложения AS .

Равновесие на отдельном товарном рынке - это состояние, когда намерения покупателей и намерения продавцов совпадают, так что ни у кого из экономических субъектов рынка нет стимулов изменить свое хозяйственное поведение. Макроэкономическое равновесие, графически оно будет означать совмещение на одном графике кривых АD и АS. Помня о нашей «синтетической» кривой АS, отражающей компромисс между различными теоретическими школами, увидим, что кривая АD может пересечь кривую АS на трех уже отрезках: горизонтальном, промежуточном или вертикальном (рис. 2).

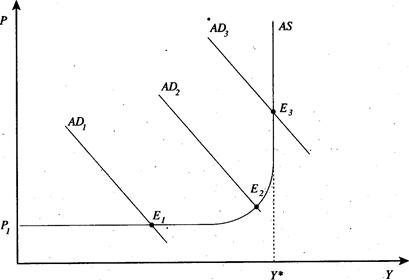
рис. 2 Макроэкономическое равновесие: модель «АD — АS»

На этом графике представлены три варианта возможного макроэкономического равновесия, т.е. такого состояния экономики, когда намерения всех покупателей приобрести созданный ВВП при данном уровне цен совпадают с намерениями всех продавцов предложить объем совокупного выпуска при том же уровне цен. Другими словами, равновесный уровень реального ВВП (Y) — это такой уровень, при котором объем произведенной продукции равен совокупному спросу на нее.

Точка Е1 — это макроэкономическое равновесие при неполной занятости без повышения уровня цен, т.е. без инфляции. Точка Е2 — это равновесие при небольшом повышении уровня цен и со­стоянии, близком к полной занятости. Точка Е3 — это равновесие в условиях полной занятости (Y*), но с инфляцией. В случае отклонения от различных равновесных состояний в точках E1, E2, и E3 приспособление экономики будет происходить по-разному. В экстремальном кейнсианском случае, когда цены и заработная плата жестки, возвращение в точку равновесия Е1 будет осуществляться за счет колебаний в объемах реального ВВП, а не колебаний цен. Фирмы будут сокращать или расширять производ­ство при неизменном уровне цен в стране.

В нормальном кейнсианском случае отклонение от точки Е2 бу­дет сопровождаться приспособлением экономики к равновесному состоянию путем изменения и уровня цен, и объемов выпуска.

В классическом случае отклонение от точки Е3 и возвращение к равновесному состоянию будет происходить только за счет измене­ния гибких цен и заработной платы без каких-либо изменений в объеме реального выпуска, поскольку экономика уже находится на уровне потенциального ВВП.

Итак, можно сделать вывод о том, что в краткосрочном периоде реальный объем ВВП определяется колебаниями совокупного спроса, так как цены и заработная плата негибки. В долгосрочном периоде, напротив, при гибкости ценового механизма реальный ВВП определяется колебаниями совокупного предложения.

1.4 МОДЕЛЬ МАКРОЭКОНОМИЧЕСКОГО РАВНОВЕСИЯ <СОВОКУПНЫЙ ДОХОД – СОВОКУПНЫЕ РАСХОДЫ> ИЛИ КЕНСИАНСКИЙ КРЕСТ

Во-первых, Кейнс, в отличие от классиков, выдвинул положе­ние о том, что не совокупное предложение определяет совокупный спрос, а, наоборот, совокупный спрос определяет уровень экономической активности, т.е. максимально возможный уровень выпуска продукции (совокупное предложение) и занятости.

Во-вторых, как нам уже известно из предыдущей лекции, Кейнс предполагал, что заработная плата и цены не обладают совершен­ной гибкостью.

В-третьих, процентная ставка, также не отличаясь гибкостью,

не уравнивает объемы инвестиций и сбережений, как это представлялось в модели классиков.

В-четвертых, полная занятость не достигается в экономике автоматически и хроническая безработица может носить затяжной характер, что дает основания для государственного вмешательства в экономические процессы.

Совокупный спрос в кейнсианской модели зависит от таких важнейших категорий, как функция потребления и функция сбережения. И потребление, и сбережение являются, по Кейнсу, функциями текущего дохода. Для лучшего понимания идей Кейнса необходимо ввести новые понятия, используемые им в его работе «Общая теория занятости, процента и денег». Во-первых, это отношение между дополнительным потреблением и дополнительным доходом – предельная склонность к потреблению МРС

МРС = ∆С/∆Y

Во-вторых, отношение между дополнительным сбережением и дополнительным доходом — предельная склонность к сбережению МРС

МРС =∆S/∆Y

Так, если дополнительный доход домашнего хозяйства состав­ляет 100 руб., из которых 75 руб. используются на потребление, а ос­тавшиеся 25 руб. — на дополнительные сбережения, то МРС соста­вит 75/100 = 0,75, а МРС - 25/100 = 0,25

Величина предельной склонности к потреблению находится между нулем и единицей: 0 < МРС < 1. Сумма МРС и МРS всегда равна единице. Это нетрудно понять, поскольку дополнительный доход тратится как на потребление, так и на сбережение в опреде­ленной пропорции.

От предельной склонности к потреблению нужно отличать сред­нюю склонность к потреблению АРС, т.е. отношение расходов на по­требление к величине дохода: АРС =С/Y

Соответственно, средняя склонность к сбережению определяется как отношение сбережения к доходу: АРS= S/Y

Для построения модели рассмотрим систему из двух уравнений:

Y= С (графически представлено линией 45°);

С == Сα + мpс Y(график функции потребления)

Например, если МРС '= 0,75, а автономное потребление — 100 млрд руб., то получаем: С = 100 + 0,75 Y. Поскольку Y= С, то, подставив вместо С символ Y, можем записать; Y == 100 + 0,75 Y - Следовательно, равновесный уровень дохода составит 400 млрд руб. Мы получили график. Пересечение линии 45° и графика потребления в точке Е означает уровень нулевого сбережения. Слева от этой точки можно наблюдать затененную область, отражающую отрицательное сбережение (т.е. расходы превышают доходы — «жизнь в долг»), а справа — сбереже­ние положительное ( рис.3).

Равновесие наблюдается в точке Е, так как только здесь доходы

и расходы равны. При уровне дохода, равном, например, 700 млрд. руб., величина потребления С составит: 100 + (0,75 х 700) == 625 млрд руб. Расстояние по вертикали между линией 45° и графиком потребления, обозначенное буквой S, — это величина сбережения, равная 75 млрд руб. (700-625).

График функции сбережения (рис. 4) показывает зависимость

сбережений от размера текущего дохода.

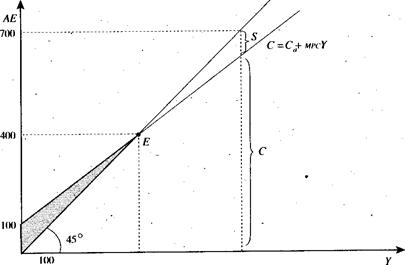
Рис.3 Кейсианский крест

Алгебраически график функции сбережения определяется по формуле:

S =-Cα + мрs Y

Наклон графика сбережений S определяется предельной склонностью к сбережению и составляет в нашем примере 0,25. При уровне дохода 700 млрд. руб. на рис. 3, сбережения составят: —100 + (0,25 х 700) = 75 млрд руб.

То, что на рис. 3 мы назвали отрицательным сбережением, очевидно на рис.4: отрицательные значения вплоть до точки пересечения графика сбережения с осью абсцисс в точке E. Автономное потребление представлено как отрицательное сбережение, при нулевом доходе, т.е. 100 млрд. руб.

Эта модель, отражающую равновесный уровень дохода с учетом только одной составляющей — потребительских расходов. Совокупные расходы включают в себя и другие компоненты. Прежде чем рассмотреть их в кейнсианской модели макроэкономического равновесия, необходимо сделать важное уточнение.

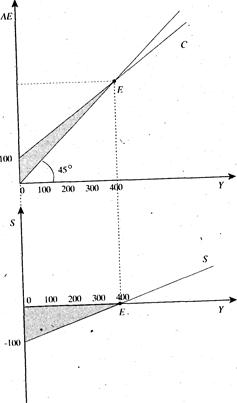
рис. 4. Функция сбережения

1.5 МАКРОЭКОНОМИЧЕСКАЯ МОДЕЛЬ ОБЩЕГО РАВНОВЕСИЯ. МУЛЬТИПЛИКАТОР

Совокупный эффективный спрос определяется как сумма потребления и инвестиций

Доход населения y распадается на одну часть, использованную на потребление , и вторую, помещенную на сбережение

Сбережения населения могут быть единственным финансовым источником инвестиций предприятий, осуществляют которые производители. Кейнс впервые обратил внимание на то, что решение производителей инвестировать может не совпадать с решением потребителей сберегать. Механизм, который обеспечивает выравнивание не обязательно совпадающих планов сбережений населения и инвестиций предприятий, Кейнс назвал мультипликатором.

Предположим, что население расходует на потребление 80% дохода, а остальные 20% сберегает. Тогда потребительская функция имеет вид

Пусть объем инвестиционной деятельности увеличился на денежных единиц. Это вызывает непосредственное увеличение дохода затронутых этим лиц на такую же сумму. В связи с увеличением доходов они увеличивают свои потребительские расходы на сумму , и на увеличиваются их сбережения. Такое увеличение спроса приведет к увеличению дохода какой-то группы лиц на сумму . Эти лица, в свою очередь, повысят свои потребительские расходы на сумму , что увеличит на еще чьи-то доходы и т.д. Общее увеличение дохода составит

.

Таким образом, первоначальное увеличение инвестиций на единиц пос­редством мультипликатора вызывает пятикратное увеличение дохода, что приводит к увеличению потребительских расходов и сбереже­ний населения. Равновесие между сбережениями и инвестициями восста­новлено. Этот процесс можно описать при помощи уравнений (1) и (2).

Равновесный национальный доход , отвечающий равенству спроса и предложения

определяется как решение уравнения

.

Приращение дохода dC

,

Или

,

Откуда

Величина показывает, насколько возрастает национальный доход при заданном росте инвестиций и поэтому называется мультипликатором.

В модель легко ввести фискальную политику государства, учи­тывая, что оно действует:

1) взимая налоги ;

2) расходуя сумму на потребление и вложение в основные фонды общественного пользования. Доход домашних хозяйств теперь

,

а функция потребления

.

Предельная склонность к потреблению

.

Равновесие благ и услуг запишется следующим образом

.

Посмотрим как изменяется в результате фискальной политики государства. Обозначим изменение через h, – вновь созданный бюджетный дефицит. Рост государственных расходов увеличивает бюджетный дефицит на величину , но так же, как и инвестиции I увеличивают национальный доход (при условии неизменности налогов и инвестиций).

Уменьшение налогов T при условии неизменности I и G также повыша­ет национальный доход, но эффект мультипликатора меньше, чем в случае повышения G.

В первом приближении

, где t – норма обложения.

Так как увеличение G приводит к росту y, то автоматически увеличивается величина взимаемого налога при заданной норме обложения t. По этому рост государственных расходов на величину вызывает бюджетный дефицит меньший, чем планируемый.

Уровень равновесия национального дохода не всегда означает хорошее состояние экономики. Главная проблема экономической жизни – это проблема совмещения в каждый момент уровня равновесия товаров и услуг с таким уровнем дохода , который обеспечивает полную занятость. Если инвестиции низки и , то это означает большую безработицу. Избыток совокупного спроса, то есть ситуация когда приводит к повышению цен, следствием которого является стремление про­изводителей больше производить товаров и соответствующего повышения зарплат. Это, в свою очередь, приводит к очередному увеличению спроса. Возникает инфляционная спираль. В этом случае государство уменьшает свои расходы G.

2. ОБЛАСТЬ ПРИМИНЕНИЯ И ОГРАНИЧЕНИЯ ИСПОЛЬЗОВАНИЯ МАКРОЭКОНОМИЧЕСКИХ МОДЕЛЕЙ ПРИ РЕШЕНИИ ЭКОНОМИЧЕСКИХ ЗАДАЧ

В настоящее время трудно назвать области экономики, как теоретической, так и практической, где не применялись бы методы математического моделирования. Анализ функционирования и исследование перспектив развития экономической системы любого уровня – предприятия, отрасли, региона, страны – предполагает построение экономико-математической модели и осуществление соответствующих исследований на ее основе.

Придавая огромное значение исследованию перспектив развития национальных экономик, правительства практически всех стран уже несколько десятилетий используют макроэкономические модели для целей имитационного прогнозирования и планирования. Именно на действующих макроэкономических моделях анализируются последствия различного рода государственных регуляторных воздействий, ожидаемых изменений во внешнем окружении, изменения основных макроэкономических тенденций и т.д. То есть, прежде чем принять решение, чрезвычайно важно проанализировать (просчитать) его последствия.

Особых успехов в применении макроэкономических моделей для целей государственного планирования и прогнозирования развития национальной экономики добились такие страны, как Франция, Япония, США. Использование макроэкономических моделей для планирования экономического развития было характерно и для бывшего Советского Союза. В настоящее время в Украине также используются макроэкономические модели для исследования и прогнозирования экономического развития Украины. Как наиболее перспективные могут быть названы действующие макроэкономические модели, предназначенные для составления среднесрочных прогнозов развития ключевых макроэкономических показателей, разработанные в Институте экономического прогнозирования НАН Украины и Институте кибернетики НАН Украины. Однако, к сожалению, в настоящее время подобные исследования в Украине носят, в основном, научный характер и не являются основой для государственного планирования и регулирования.

Достижения макроэкономикой равновесия во всех аспектах, формах и результатах тождественно понятию оптимальности хозяйственной системы. Теоретические модели макроэкономического равновесия позволяют полнее представить возможные направления воздействия на хозяйственные процессы в целях рационализации использования ресурсов, максимизации доходов, повышения уровня жизни и благосостояния.

Существуют отправные точки анализа макроэкономического равновесия, представленные моделями Л. Вальраса, Д. Кейнса, В. Леонтьева и других авторов. Каждая из моделей имеет свои возможности и пределы понимания равновесия. Поэтому целесообразно их совместное применение, что позволяет разностороннее и содержательнее воспринимать существующие нерешенные проблемы.

Теоретическая идея макроэкономического равновесия находит практическую реализацию в системе национальных счетов. СНС раскрывает фактические показатели, стандартизованные технологии расчета которых дают информационную базу для принятия ответственных решений в области экономической политики.

Эконометрическая модель экономики России.

Предполагаемое назначение модели: сценарные прогнозы на период от квартала до 2-х – 3-х лет. Отличие этой модели от известных подобных будет в ее оснащении специальным «настройщиком», обеспечивающим даже начальное ее применение при минимальном авторском сопровождении. Модель, в частности, даст возможность:

– строить многовариантные точечные и интервальные прогнозы основных показателей экономики (ВВП, выпуски по отраслям, импорт, экспорт и т.д.) при инерционном сценарии ее развития;

– проводить сценарный анализ влияния параметров бюджетно-налоговой и социальной политики, тарифной политики естественных монополий и т.п. на показатели развития экономики;

– прогнозировать последствия от изменений на мировых рынках энергоресурсов, от динамики валютных курсов, от экспортно-импортных политик и т.п.

– выявлять траектории в пространстве параметров бюджетной, кредитно-денежной и социальной политик, позволяющих за ограниченное число тактов времени достичь заданных целей.

Предполагается, что «ядро» модели будет состоять примерно из 100 уравнений.

Модель общего равновесия (CGE-модель-Валовой внутренний продукт).

В основе таких моделей лежит идея стремления субъектов экономики к общему равновесию спроса и предложения на всех рынках взаимодействия. Имея практический опыт построения и применения такого рода моделей (модели RUSEC, RUSEC-GAZPROM, ЦЕНТР-ФЕДЕРАЛЬНЫЕ ОКРУГА) предполагаем, что для Минэкономразвития необходима как базовая модель не менее