Методы приближённого решения матричных игр
«Теория игр – раздел математики, предметом которого является изучение математических моделей принятия оптимальных решений в условиях конфликта...». (17)
Математическая теория игр способна не только указать оптимальный путь к решению некоторых проблем, но и прогнозировать их исход. Матричные игры серьёзно изучаются специалистами, так как они довольно просты и к ним могут быть сведены игры общего вида. Поэтому теория матричных игр хорошо развита, существуют различные методы поиска решения игр.
Но в большинстве случаев решение матричных игр представляет собой трудный и громоздкий процесс. Есть примеры, когда даже для матриц размера 3´3, процесс поиска решения довольно трудоёмкий.
Кроме того, выигрыши игроков в каждой ситуации не всегда определяются точными измерениями. В процессе сбора данных об изучаемом явлении, анализа этих данных и введения при построении модели различных предположений накапливаются ошибки. Они же могут выражаться числами в матрице выигрышей. Поэтому точность в определении значения игры и оптимальных стратегий игроков оправдана не всегда.
А также, следует заметить, что погрешность в оценке игроком своего выигрыша не может привести к практически серьёзным последствиям и небольшое отклонение игрока от оптимальной стратегии не влечёт за собой существенного изменения в его выигрыше.
Поэтому возникает потребность в разработке численных методов решения матричных игр. В настоящее время в теории игр известны несколько способов приближенного решения матричных игр.
Цель выпускной квалификационной работы изучить некоторые методы приближённого решения матричных игр, обосновать их алгоритмы, и, по возможности, реализовать на языке программирования.
Работа состоит из введения, трёх параграфов и приложения, в котором приведена программа на языке Turbo Pascal, позволяющая находить приближённое решение матричной игры.
В первом параграфе приведены основные понятия и утверждения теории матричных игр.
Параграф второй посвящён изложению приближённого решения игры методом Брауна-Робинсона (метод фиктивного разыгрывания) и его обоснованию. Приведён пример применения алгоритма для конкретной матричной игры.
В третьем параграфе рассмотрен ещё один метод – монотонный итеративный алгоритм приближённого решения матричных игр.
§1. Основные понятия
Будем рассматривать только парные антагонистические игры, т. е. игры в которых участвуют только два игрока – две противоборствующие стороны и выигрыш одного из игроков равен проигрышу другого. Кроме того, будем считать, что каждый игрок имеет лишь конечное число стратегий:
U1={a1, a2,..., am} – множество стратегий первого игрока;
U2={b1, b2, ... bn} – множество стратегий второго игрока.
Будем называть эти стратегии чистыми в отличие от смешанных, которые будут введены далее.
Множество U1×U2 – декартово произведение множеств стратегий игроков называется множеством ситуаций в игре. Для каждой ситуации должен быть определён итог игры. Так как игра антагонистическая достаточно определить выигрыш а одного из игроков, скажем первого. Тогда выигрыш второго игрока будет равен (-а). Таким образом, имеем матрицу выигрышей первого игрока ( для второго игрока матрица выигрышей будет -А):
![]() A=
A= 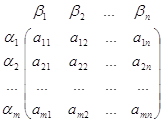
Определение.Система Г={U1, U2, A} называется матричной игрой двух лиц.
Разыгрывание матричной игры сводится к выбору игроком 1 i-ой строчки матрицы выигрышей, а игроком 2 - j-го столбца. После этого игрок 1 получает выигрыш равный аij, а игрок 2 – (-аij).
При правильной игре игрок 1 может всегда гарантировать себе выигрыш, который назовём нижним значением цены игры. Обозначим его: ![]() .
.
В свою очередь, игрок 2 может гарантировать себе проигрыш, который назовём верхним значением цены игры. Обозначим его:
![]() .
.
Чистые стратегии i* и j*, соответствующие ![]() называются максиминной и минимаксной стратегиями.
называются максиминной и минимаксной стратегиями.
Лемма 1.В матричной игре ![]() . (17)
. (17)
Определение.Ситуация (i*, j*) называется ситуацией равновесия, если для iÎ1,2,…,m, jÎ1,2,…,выполняется неравенство:
![]() .
.
Ситуация равновесия это такая ситуация, от которой ни одному из игроков не выгодно отклоняться. В этом случае стратегии i*, j* называют оптимальными стратегиями игроков.
Чтобы такая ситуация существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. ![]() .(17)
.(17)
Определение. Пусть(i*, j*) - ситуацией равновесия в матричной игре. Тогда число ![]() называется значением или ценой игры.
называется значением или ценой игры.
Например, в игре ГА с матрицей А=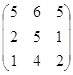 существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
существует не одна ситуация равновесия. В данной игре их две: (1, 1) и (1, 3).
Множество всех ситуаций равновесия в матричной игре обозначим через Z(Г).
Лемма о масштабе 1.Пусть Г и Г/ - две матричные игры с матрицей выигрышей А={aij} и A/={a/ij}, причём А/=А+ a, =const, a=const.
Тогда Z(Г)=Z(Г/) и /= +a (где / - значение цены игры Г/, - значение цены игры Г). (17)
Эта лемма имеет большое практическое значение, так как большинство алгоритмов для решения матричных игр основано на предположении, что матрица игры положительна. В случае, когда матрица имеет неположительные элементы, следует прибавить ко всем элементам матрицы число наибольшее по абсолютной величине, из всех отрицательных элементов.
Существуют игры, в которых ситуации равновесия в чистых стратегиях не существует. Тогда игрокам бывает не выгодно придерживаться своих минимаксных и максиминных стратегий, так как они могут получить больший выигрыш, отклонившись от них. В этом случае игрокам разумно действовать случайно, т. е. выбирать стратегии произвольно и не сообщать о выборе сопернику. Такие стратегии игроков будем называть смешанными.
Определение. Смешанной стратегией игрока называется полный набор вероятностей применения его чистых стратегий.
Так если игрок 1 имеет m чистых стратегий, то его смешанная стратегия x – это набор чисел x=(x1,x2,…,xm), которые удовлетворяют соотношениям ![]() ,
, ![]() =1. Аналогичным образом определяется смешанная стратегия y игрока 2.
=1. Аналогичным образом определяется смешанная стратегия y игрока 2.
Определение.Оптимальными стратегиями игроков называются стратегии, которые при многократном повторении обеспечивают игрокам максимально возможный средний выигрыш (или минимально возможный средний проигрыш).
Таким образом, процесс игры при использовании игроками своих смешанных стратегий превращается в случайное испытание, которое назовём ситуацией в смешанных стратегиях. Она обозначается так (x, y), гдеx и y – смешанные стратегии игроков 1 и 2 соответственно.
Для ситуации в смешанных стратегиях каждый игрок определяет для себя средний выигрыш, который выражается в виде математического ожидания его выигрышей:![]() .
.
От матричной игры пришли к новой игре ![]() ={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
={X, Y, K}, где X, Y – множества смешанных стратегий игроков, а K – функция выигрышей в смешанных стратегиях. Такую игру называют смешанным расширением матричной игры.
Цели игроков остаются прежними: игрок 1 желает получить максимальный выигрыш, а игрок 2 стремится свести свой проигрыш к минимуму. Поэтому для смешанного расширения игры, аналогичным образом определяются верхнее и нижнее значение цены игры, только теперь игроки выбирают свои смешанные стратегии. Обозначим их:
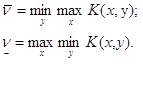
В этом случае остаётся справедливой лемма 1, т. е.![]() .
.
Определение. Ситуация (x*, y*) в игре образует ситуацию равновесия, если для всех xÎX, yÎY выполняется равенство:
K(x, y*)≤K(x*,y*)≤K(x*,y).
Чтобы ситуация равновесия в смешанном расширении игры существовала необходимо и достаточно равенство верхней и нижней цен игры, т. е. ![]() , где n - цена игры.
, где n - цена игры.
Для случая смешанного расширения игры также справедлива лемма о масштабе.
Лемма о масштабе 2.
Пусть ГА и ГА/ - две матричные игры А/=aА+ В, , a=const, В – матрица с одинаковыми элементами , т. е. ij= для всех i, j.
Тогда Z(![]() )=Z(ГА/) и А/= aА+ (где А/ - значение цены игры ГА/, А - значение цены игры ГА). (17)
)=Z(ГА/) и А/= aА+ (где А/ - значение цены игры ГА/, А - значение цены игры ГА). (17)
Теорема. В смешанном расширении матричной игры всегда существует ситуация равновесия. (17)
§2. Итеративный метод Брауна-Робинсона (метод фиктивного разыгрывания)
Часто в практических задачах нет необходимости находить точное решение матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш, близкий к цене игры и приближённые оптимальные стратегии игроков.
Ориентировочное значение цены игры может дать уже простой анализ матрицы выигрышей и определение нижней и верхней цен игры. Если они близки, то поисками точного решения заниматься не обязательно, так как достаточно выбрать чистые минимаксные стратегии. Если же они не близки, можно получить приемлемое для практики решение с помощью численных методов решения игр, из которых рассмотрим метод итераций.
Пусть разыгрывается матричная игра ГА с матрицей А={aij} размера (m´n). Идея метода – многократное фиктивное разыгрывание игры с заданной матрицей. Одно разыгрывание игры будем называть партией, число которых неограниченно.
В 1-ой партии оба игрока выбирают совершенно произвольные чистые стратегии. Пусть игрок 1 выбрал i-ю стратегию, а игрок 2 – j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той своей стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на этот ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия.
С ростом числа шагов процесса смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Этот процесс приближённого нахождения оптимальных стратегий игроков называется итеративным , а его шаги – итерациями.
Итак, предположим, что за первые k разыгрываний игрок 1 использовал i-ю чистую стратегию ![]() ikраз (i=1,…,m), а игрок 2 j-ю чистую стратегию
ikраз (i=1,…,m), а игрок 2 j-ю чистую стратегию ![]() раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы
раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы ![]() .
.
Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. Поэтому в ответ на применение игроком 2 своей смешанной стратегии yk, он будет использовать чистую стратегию ik+1 , которая обеспечит ему лучший результат при разыгрывании (k+1)-ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:
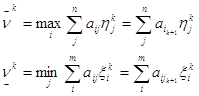
где ![]() - наибольшее значение проигрыша игрока 2 и
- наибольшее значение проигрыша игрока 2 и ![]() - наименьшее значение выигрыша игрока 1.
- наименьшее значение выигрыша игрока 1.
Рассмотрим отношения, которые определяют средние значения проигрыша игрока 2 и выигрыша игрока 1:
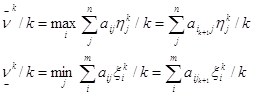
Пусть ν - цена матричной игры ГА. Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т. е.
![]() . (1)
. (1)
Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала
![]() .
.
Сходимость алгоритма гарантируется следующей теоремой.
Теорема.![]() .
.
Схема доказательства.
Лемма. Для всякой матрицы А и "e>0 существует такое k0, что
![]() .
.
При предельном переходе в неравенстве (1) при k®¥ имеем:
![]() . (2)
. (2)
Отсюда получаем оценку разности пределов:
![]() .
.
Из леммы следует, что
![]() .
.
На основании неравенства (1) имеем: 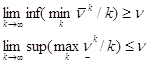 .
.
Следовательно, в силу ограниченности пределов
![]() .
.
Получаем оценку для разности пределов:
![]() для "e>0.
для "e>0.
Можем заключить, что ![]() . Осталось показать равенство пределов . Это следует из неравенства (2).
. Осталось показать равенство пределов . Это следует из неравенства (2).
Итак, ![]() .
.
Пример.Найти приближённое решение игры с матрицей
А=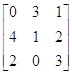 .
.
Пусть игру начнёт игрок 2. Он произвольно выбирает одну из своих чистых стратегий. Предположим, что он выбрал свою 1-ю стратегию, а игрок 1 отвечает своей 2-й стратегией. Занесём данные в таблицу.
но-мер пар тии | стратегия второго игрока | выигрыш игрока 1 при его стратегиях | стратегия первого игрока | проигрыш игрока 2 при его стратегиях | u | w | n | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||||||
| 1 | 1 | 0 | 4 | 2 | 2 | 4 | 1 | 2 | 4 | 1 | 5/2 |
В столбце u находится наибольший средний выигрыш 4 игрока 1, полученный им в первой партии; в столбце w стоит наименьший средний проигрыш 1, полученный игроком 2 в первой партии; в столбце n находится среднее арифметическое n=(u+w)/2=5/2, т. е. приближенное значение цены игры, полученное в результате проигрывания одной партии.
Так как игрок 1 выбрал 2-ю стратегию, то игрок 2 может проиграть:
4, если применит свою 1-ю стратегию;
1, если применит свою 2-ю стратегию;
2, если применит свою 3-ю стратегию.
Поскольку он желает проиграть как можно меньше, то в ответ применит свою 2-ю стратегию.
Тогда первый игрок получит выигрыш равный 3, 1, 0 соответственно при своих 1-й, 2-й, 3-й стратегиях, а его суммарный выигрыш за две партии составит:
0+3=3 при его 1-й стратегии;
4+1=5 при его 2-й стратегии;
2+0=2 при его 3-й стратегии.
Из всех суммарных выигрышей наибольшим является 5, который получается при 2-й стратегии игрока 1. Значит, в этой партии он должен выбрать именно эту стратегию.
При 1-й стратегии игрока 1 игрок 2 проигрывает 4, 1, 2 соответственно 1-й, 2-й, 3-й его стратегиям, а суммарный проигрыш за обе партии составит:
4+4=8 при его 1-й стратегии;
1+1=2 при его 2-й стратегии;
2+2=4 при его 3-й стратегии.
Все полученные данные занесём в таблицу. В столбец u ставится наибольший суммарный выигрыш игрока 1 за две партии, деленный на число партий, т. е. 5/2; в столбец w ставится наименьший суммарный проигрыш игрока 2, деленный на число партий, т. е. 2/2; в столбец n ставится среднее арифметическое этих значений, т. е. 7/2.
но-мер пар тии | стратегия второго игрока | выигрыш игрока 1 при его стратегиях | стратегия первого игрока | проигрыш игрока 2 при его стратегиях | u | w | n | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||||||
1 2 | 1 2 | 0 3 | 4 5 | 2 2 | 2 2 | 4 8 | 1 2 | 2 4 | 4 5/2 | 1 2/2 | 5/2 7/2 |
В третьей партии игрок 2 выбирает свою 2-ю стратегию, так как из всех суммарных проигрышей наименьшим является 2.
Таким образом, продолжая этот процесс далее, составим таблицу разыгрываний игры за 20 итераций (партий).
но-мер пар тии | Страте- гия второго игрока | выигрыш игрока 1 при его стратегиях | Страте- гия первого игрока | проигрыш игрока 2 при его стратегиях | u | w | n | ||||
| 1 | 2 | 3 | 1 | 2 | 3 | ||||||
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 1 2 2 2 3 3 1 3 3 3 3 3 2 2 2 2 2 2 2 3 | 0 3 6 9 10 11 11 12 13 14 15 16 19 22 25 28 31 34 37 38 | 4 5 6 7 9 11 15 17 19 21 23 25 26 27 27 29 30 31 32 34 | 2 2 2 2 5 8 10 13 16 19 22 25 25 25 25 25 25 25 25 28 | 2 2 1 1 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 1 | 4 8 8 8 8 8 12 16 20 24 28 32 36 40 44 48 48 48 48 48 | 1 2 5 8 11 14 15 16 17 18 19 20 21 22 23 24 27 30 33 36 | 2 4 5 6 7 8 10 12 14 16 18 20 22 24 26 28 29 30 31 32 | 4 5/2 6/3 9/4 10/5 11/6 15/7 17/8 19/9 21/10 23/11 25/12 26/13 27/14 27/15 29/16 31/17 34/18 37/19 38/20 | 1 2/2 5/3 6/4 7/5 8/6 10/7 12/8 14/9 16/10 18/11 20/12 21/13 22/14 23/15 24/16 27/17 30/18 31/19 32/20 | 5/2 7/2 11/6 15/8 17/10 19/12 25/14 27/16 33/18 37/20 41/22 45/24 47/26 49/28 50/30 53/32 58/34 64/36 68/38 70/40 |
Из таблицы видно, что в 20-ти проигранных партиях стратегии 1, 2, 3 для второго игрока встречаются соответственно 2, 10, 8 раз, следовательно, их относительные частоты равны 2/20, 10/20, 8/20. Стратегии 1, 2, 3 для игрока 1 встречаются соответственно 8, 12, 0 раз, следовательно, их относительные частоты равны 8/20, 12/20, 0, а приближённое значение цены игры равно 70/40.
Таким образом, получили приближённое решение игры: x20=(1/10, 1/2, 2/5), y20=(2/5, 3/5, 0), n=1,57.
Такой итеративный процесс ведёт игроков к цели медленно. Часто для получения оптимальных стратегий, дающих игрокам выигрыш, приходится проделывать сотни итераций. При этом скорость сходимости заметно ухудшается с ростом размерности матрицы и ростом числа стратегий игроков. Это также является следствием не монотонности последовательностей ![]() и
и ![]() . Поэтому, практическая ценность этого метода имеет место, когда вычисления проводятся на достаточно быстродействующих вычислительных машинах. Но наряду с таким недостатком можно выделить и достоинства метода итераций:
. Поэтому, практическая ценность этого метода имеет место, когда вычисления проводятся на достаточно быстродействующих вычислительных машинах. Но наряду с таким недостатком можно выделить и достоинства метода итераций:
1. Этот метод даёт возможность найти ориентировочное значение цены игры и приближённо вычислить оптимальные стратегии игроков.
2. Сложность и объём вычислений сравнительно слабо возрастают по мере увеличения числа стратегий игроков (m и n).
Для рассмотренного алгоритма приведена реализация на языке Pascal (см. приложение).
§3. Монотонный итеративный алгоритм решения матричных игр
Предлагаемый для рассмотрения алгоритм реализуется только для одного игрока в отличие от первого, который работает для двух игроков. Алгоритм позволяет находить точно и приближенно оптимальную стратегию игрока 1 и значение цены игры n. С помощью алгоритма можно получить заданную точность решения, причём число шагов, необходимых для достижения результатов, слабо зависит от размерности матрицы выигрышей.
Особенность этого алгоритма в способности генерировать строго монотонно возрастающую последовательность оценок цены игры, что не свойственно ранее предлагаемому алгоритму.
Рассмотрим смешанное расширение ![]() =(X,Y,K) матричной игры ГА с матрицей А размера (m´n). Процесс разыгрывания игры состоит из нескольких шагов. Пусть каждый из игроков имеет конечное число стратегий.
=(X,Y,K) матричной игры ГА с матрицей А размера (m´n). Процесс разыгрывания игры состоит из нескольких шагов. Пусть каждый из игроков имеет конечное число стратегий.
Введём следующие обозначения:
аi – i-я строка матрицы выигрышей;
xN=(x1N,x2N,…,xmN) ÎX – m-мерный вектор, приближение оптимальной стратеги первого игрока на N-шаге (N-номер шага);
cN=(![]() ) –n-мерный вектор, определяющий средний накопленный выигрыш на N-шаге.
) –n-мерный вектор, определяющий средний накопленный выигрыш на N-шаге.
Зададим начальные условия. Пусть на 0-шаге с0=![]() , x0=(0,…, 1,…, 0), где 1 занимает i0-ю позицию.
, x0=(0,…, 1,…, 0), где 1 занимает i0-ю позицию.
Определим итеративный процесс следующим образом: по известным векторам xN-1, cN-1 находим векторы xNи cN , которые вычисляются по следующим формулам:
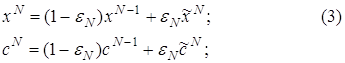
![]() где параметр 0£eN£1, а векторы
где параметр 0£eN£1, а векторы ![]() вводятся далее.
вводятся далее.
Как отмечалось, вектор сN определяет средний накопленный выигрыш игрока 1 на N шаге. Компоненты этого вектора – это числа. В худшем случае игрок 1 может получить минимальное из этих чисел. Примем его за нижнюю оценку цену игры, которую обозначим:
![]() . (4)
. (4)
Запомним множество индексов JN-1=( Далее рассмотрим подыгру ГN игрыГА с матрицей выигрышей АN={ После нахождения И рассмотрим игру (2´n), в которой у игрока 1 две чистые стратегии, а у игрока 2 – n чистых стратегий. Эта игра задаётся матрицей Далее вычисляем xN, сN и переходим к следующему шагу. Процесс продолжаем до тех пор, пока не выполнится равенство eN=0, потому что по теореме о минимаксе Сходимость алгоритма гарантируется теоремой. Теорема. Пусть {xN}, {N} – последовательности, определяемые равенствами (3), (4) . Тогда справедливы следующие утверждения: 1. 2. 3. Доказательства этой теоремы достаточно рутинно. Его можно посмотреть в (15). Рассмотрим применение этого алгоритма к решению конкретной задачи. Пример.Решить игру с матрицей А= Итерация 0. 1. Пусть игрок 1 выбрал свою 1-ю стратегию, т. е. А0=(0, 1, 2). Тогда за начальные условия примем следующие: x0=(1, 0, 0) – приближение оптимальной стратегии игрока 1; c0=a1=(0, 1, 2) – возможный выигрыш игрока 1. Найдём множество индексов 2. На этом шаге определим, пользуясь начальными значениями, компоненты векторов Обозначим её через 3. Найдём e1. Для этого рассмотрим подыгру (2´3) с матрицей 4. Проведённые вычисления позволяют найти значения векторов x1, c1: x1=1/2x0+1/2 c1=1/2c0+1/2 Итерация 1. Так как e1 не равно 0, то процесс продолжается дальше. Теперь за начальные условия примем найденные значения векторов x1, c1. С их помощью вычисляем 1. Итак, пусть x1=(1/2, 1/2, 0), c1=(2, 3/2, 3/2). Найдём множество индексов 2. Далее найдём компоненты векторов =(4/2, 3/2, 3/2). 3. Вычислим коэффициент e2. Для этого решим подыгру (2´3): Итак, оптимальной стратегией игрока 1 является x*=x1=(1/2,1/2, 0) и На первый взгляд алгоритм практически трудно реализовать, так как не известно, какого размера будет получена матрица для подыгры ГN. Но на самом деле с вероятностью 1 на каждом шаге придётся решать подыгру размера не больше чем m´2.(9) Инженерами-программистами алгоритм был реализован на языке программирования Фортран-IV. Вычислительные эксперименты, проведённые на ЭЦВМ ЕС-1030, показали, что для игр размерности от 25´25 до 100´100, элементы, матрицы выигрышей которых были заполнены случайными числами, алгоритм позволяет найти искомое приближение за 100-1000 итераций, причём их число слабо зависит от размера матрицы. Для решения одной задачи машина затрачивает не дольше 8 минут. Ими же были разработаны различные модификации алгоритма. (9) Приложение В приложении приведена реализация итеративного метода Брауна-Робинсона решения матричных игр на языке программирования Turbo Pascal 7.0. Пользователь вводит матрицу выигрышей размера m×n, где m≥3, n≥3. Далее машина запрашивает информацию о том, кто из игроков начинает игру, какую стратегию он выбирает и количество итераций. На дисплее выводится таблица разыгрываний игры за определённое число итераций. program br; uses crt; const matr1:array(1..3,1..3) of byte=((0,4,2), (3,1,0), (1,2,3)); {Начальнаяматрица} var matr:array (1..10,1..10) ofinteger; {Матрица, введенная пользователем} win_one:array(0..150,1..10) of word; {Массивдлявыигрышейигр.1} win_two:array(0..150,1..10) of word; {Массивдлявыигрышейигр.2} max,min:integer; a,i,j,m,n,pl,st,st1,st2,kl:byte; nol,otr:boolean; functionigr_one:byte; {Функция определения следующего} var a1,a2,max:integer; {ходадляигрока 1} begin max:=win_one(a,1); igr_one:=1; if pl=1 then a2:=m else a2:=n; for a1:=1 to a2 do if win_one(a,a1)>max then begin max:=win_one(a,a1); igr_one:=a1; end; end; function igr_two:byte; {Функция определения следующего} var a1,a2,min:integer; {ходадляигрока 2} begin min:=win_two(a,1); igr_two:=1; if pl=1 then a2:=n else a2:=m; for a1:=1 to a2 do if win_two(a,a1) min:=win_two(a,a1); igr_two:=a1; end; end; begin clrscr; writeln ('Итеративный метод Брауна-Робинсона.'); writeln('Матрица пользователя? (y/n)'); if (readkey='y')or(readkey='Y') then begin {Матрица из памяти или вводит пользователь} write ('Введите размеры матрицы:'); readln(n,m); {Ввод количества строк и столбцов} writeln('Введите ',n,' строки по ',m,' элементов:'); nol:=true; otr:=false; min:=0; for j:=1 to n do for i:=1 to m do begin {Вводэлементовматрицы} read(matr(i,j)); ifmatr(i,j)<>0 thennol:=false; {Установка флага, что не все элементы равны 0} ifmatr(i,j)<0 thenotr:=true; {Установка флага наличия отрицательных элементов} ifmatr(i,j)<minthenmin:=matr(i,j);{Определение минимального элемента} end end else begin {Иначе берем матрицу из константы} n:=3;m:=3; for i:=1 to m do for j:=1 to n do matr(i,j):=matr1(i,j); end; clrscr; writeln ('Итеративный метод Брауна-Робинсона.'); if nol then writeln('Все элементы матрицы равны 0!') else begin {если установлен флаг нуля, то алгоритм не работает} if otr then for j:=1 to n do for i:=1 to m do matr(i,j):=matr(i,j)-min;{еслиестьотрицательныеэлементы,} writeln('Начальная матрица:'); {Вывод окончательной матрицы} for j:=1 to n do begin for i:=1 to m do write(matr(i,j):4); writeln; end; write('Какой игрок начнет игру? '); {Вод стартовых значений} readln(pl); write('Какую стратегию выберет ',pl,' игрок? '); readln(st); write('Количество итераций? '); readln(kl); a:=1; {заглавие таблицы} writeln(' № стр. выигрыш 1-го игр. стр. выигрыш 2-го игр. V W Y'); repeat write(a:2,st:6,' '); {формирование таблицы: номер итерации, стратегия 1игр.} if pl=2 then begin for i:=1 to n do begin win_one(a,i):=matr(st,i)+win_one(a-1,i);{формированиематрицывыигрышей 1 игр.} write(win_one(a,i):4); {выводнаэкран} end; st1:=igr_one; {определение ответной стратегии 2 игр.} gotoxy(32,wherey); write(st1:10,' '); {вывод на экран} for i:=1 to m do begin win_two(a,i):=matr(i,st1)+win_two(a-1,i); {формированиематрицывыигрышей 2 игр.} write(win_two(a,i):4); {выводнаэкран} end; gotoxy(64,wherey); write(win_one(a,st1):4); {вывод наибольшего суммарного выигрыша 1 игр.} st:=igr_two; {определение ответной стратегии 1 игр.} write(win_two(a,st):4); {вывод наибольшего суммарного выигрыша 2 игр.} write((win_one(a,st1)+win_two(a,st))/(a*2):6:2);{приближенноезначениеценыигры} end else begin for i:=1 to m do begin win_one(a,i):=matr(i,st)+win_one(a-1,i);{формированиематрицывыигрышей 1 игр.} write(win_one(a,i):4); end; st1:=igr_one; {определение ответной стратегии 2 игр.} gotoxy(32,wherey); write(st1:10,' '); for i:=1 to n do begin win_two(a,i):=matr(st1,i)+win_two(a-1,i);{формированиематрицывыигрышей 2 игр.} write(win_two(a,i):4); end; gotoxy(64,wherey); write(win_one(a,st1):4); {вывод наибольшего суммарного выигрыша 1 игр.} st:=igr_two; {определение ответной стратегии 1 игр.} write(win_two(a,st):4); {вывод наибольшего суммарного выигрыша 2 игр.} write((win_one(a,st1)+win_two(a,st))/(a*2):6:2);{приближенноезначениеценыигры} end; a:=a+1; {увеличение счетчика итераций} writeln; until a=kl+1; end; readln; readln; end. Список литературы 1. Беленький В.З. Итеративные методы в теории игр и программировании. М.: «Наука», 1977 2. Блекуэлл Д.А. Теория игр и статистических решений. М., Изд. иностранной литературы, 1958 3. Вентцель Е.С. Элементы теории игр. М., Физматгиз, 1961 4. Вилкас Э.И. Оптимальность в играх и решениях. М.: «Наука», 1986 5. Воробьёв И.Н. Математическая теория игр. М.: «Знание», 1976 6. Давыдов Э.Г. Методы и модели теории антагонистических игр. М.: «Высшая школа», 1990 7. Дрешер М. Стратегические игры. Теория и приложения. М., 1964 8. Исследование операций в экономике / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман. М.: «Банки и биржи», Юнити, 1997 9. Итеративный алгоритм решения матричных игр// Доклады Академии наук СССР, том 238, №3, 1978 10. Карлин С. Математические методы в теории игр, программировании и экономике. М.: «Мир», 1964 11. Крапивин В.Ф. Теоретико-игровые методы синтеза сложных систем в конфликтных ситуациях. М.: «Советское радио», 1972 12. Крушевский А.В. Теория игр: (Учебное пособие для вузов). Киев: «Вища школа», 1977 13. Льюис Р., Райфа Х. Игры и решения. М.,1961 14. Морозов В.В., Старёв А.Г., Фёдоров В.В. Исследование операций в задачах и упражнениях. М.: «Высшая школа», 1996 15. Матричные игры. (Сборник переводов). Под ред. Воробьёва И.Н. М., Физматгиз, 1961 16. Оуэн Г. Теория игр. (Учебное пособие). М.: «Мир», 1973 17. Петросян Л.А., Зенкевич Н.А., Семен Е.А. Теория игр. М., 1989 18. Школьная энциклопедия математика. Ред. С. М. Никольский, М.: 1996, с. 380![]() ), (k
), (k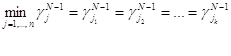 .
.![]() }, i=1,…,m, jN-1ÎJN-1. Матрица выигрышей состоит из столбцов данной матрицы, номера которых определяются множеством индексов JN-1. В этой подыгре ГN находим одну из оптимальных смешанных стратегий игрока 1:
}, i=1,…,m, jN-1ÎJN-1. Матрица выигрышей состоит из столбцов данной матрицы, номера которых определяются множеством индексов JN-1. В этой подыгре ГN находим одну из оптимальных смешанных стратегий игрока 1: ![]() .
. ![]() , находим вектор
, находим вектор ![]() по правилу:
по правилу:![]() .
.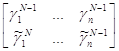 , решая которую, находим вероятность использования игроком 1 своей стратегии. Это даёт нам коэффициент eN.
, решая которую, находим вероятность использования игроком 1 своей стратегии. Это даёт нам коэффициент eN.![]() , а их равенство (что и нужно) достигается в этом случае, или пока не будет достигнута требуемая точность вычислений.
, а их равенство (что и нужно) достигается в этом случае, или пока не будет достигнута требуемая точность вычислений. ![]() т. е. последовательность {N-1} строго монотонно возрастает.
т. е. последовательность {N-1} строго монотонно возрастает.![]()
![]() , где x*ÎX* – оптимальная стратегия игрока 1.
, где x*ÎX* – оптимальная стратегия игрока 1.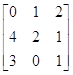 .
.![]() , на которых игрок 1 может получить, в худшем случае, наименьший выигрыш:
, на которых игрок 1 может получить, в худшем случае, наименьший выигрыш: ![]() , значит множество индексов J0={1}. Для этого индекса выигрыш равен 0. Это есть значение нижней оценки цены игры, т. е.
, значит множество индексов J0={1}. Для этого индекса выигрыш равен 0. Это есть значение нижней оценки цены игры, т. е. ![]() .
.![]() . Для этого рассмотрим подыгру
. Для этого рассмотрим подыгру 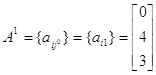 . Для этой подыгры оптимальной стратегией игрока 1 будет его 2-ая стратегия, так как она принесёт ему наибольший выигрыш.
. Для этой подыгры оптимальной стратегией игрока 1 будет его 2-ая стратегия, так как она принесёт ему наибольший выигрыш. ![]() :
: ![]() =(0, 1, 0). Зная
=(0, 1, 0). Зная ![]() , можем вычислить
, можем вычислить ![]() =0а1+1а2+0а3=а2=(4, 2, 1).
=0а1+1а2+0а3=а2=(4, 2, 1).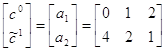 . Решая матрицу графическим способом, получаем, что e1=1/2.
. Решая матрицу графическим способом, получаем, что e1=1/2. ![]() =1/2(1, 0, 0)+1/2(0, 1, 0)=(1/2, 1/2, 0);
=1/2(1, 0, 0)+1/2(0, 1, 0)=(1/2, 1/2, 0);![]() =1/2(0, 1, 2)+1/2(4, 2, 1)=(2, 3/2, 3/2).
=1/2(0, 1, 2)+1/2(4, 2, 1)=(2, 3/2, 3/2).![]() , которые с большей точностью будут близки к истинным оптимальным стратегиям игрока 1.
, которые с большей точностью будут близки к истинным оптимальным стратегиям игрока 1. ![]() , на которых игрок 1 может получить наименьший выигрыш:
, на которых игрок 1 может получить наименьший выигрыш: ![]() , значит, J1={2,3}. Для этих индексов выигрыш равен 3/2. Это есть значение нижней оценки цены игры, т. е.
, значит, J1={2,3}. Для этих индексов выигрыш равен 3/2. Это есть значение нижней оценки цены игры, т. е. ![]() . Заметим, что
. Заметим, что ![]() .
. ![]() . Для этого рассмотрим подыгру
. Для этого рассмотрим подыгру 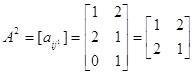 . В силу симметричности матрицы ее решением будет вектор (1/2, 1/2), т. е.
. В силу симметричности матрицы ее решением будет вектор (1/2, 1/2), т. е. ![]() 1/2a1+1/2a2+0a3=
1/2a1+1/2a2+0a3=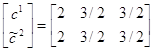 . Стратегии игроков совпадают, поэтому e2=0. В этом случае цена игры совпадает со своим нижним значением, т. е.
. Стратегии игроков совпадают, поэтому e2=0. В этом случае цена игры совпадает со своим нижним значением, т. е.![]() . Возвращаемся к предыдущему шагу.
. Возвращаемся к предыдущему шагу.![]() .Задача решена.
.Задача решена.
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Методы решения алгебраических уравнений
- Методы решения краевых задач, в том числе "жестких" краевых задач
- Минимальные формы булевых многочленов
Булевы алгебры – это решетки особого типа, которые применяются при исследовании логики (причем как логики человеческого мышления, так и
- Пересечение кривых поверхностей
- Перпендикулярность геометрических элементов
План1. Теорема о проецировании прямого угла2. Главные линии плоскости 3. Прямая, перпендикулярная к плоскости4. Перпендикулярные плоскост
- Плоские кривые
1. История изучения плоских кривыхПонятие линии определилось в сознании человека в доисторические времена. Траектория брошенного камня
- Побудова зображень предметів на площині
Житомирський Військовий ІнститутНаціонального Авіаційного УніврситетуРефератна тему:Побудова зображень предметів на площиніЖитомир
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

