Скачать

Методы решения краевых задач, в том числе "жестких" краевых задач

На примере системы дифференциальных уравнений цилиндрической оболочки ракеты – системы обыкновенных дифференциальных уравнений 8-го порядка (после разделения частных производных).

Система линейных обыкновенных дифференциальных уравнений имеет вид:

Y(x) = A(x) ∙ Y(x) + F(x),

где Y(x) – искомая вектор-функция задачи размерности 8х1, Y(x) – производная искомой вектор-функции размерности 8х1, A(x) – квадратная матрица коэффициентов дифференциального уравнения размерности 8х8, F(x) – вектор-функция внешнего воздействия на систему размерности 8х1.

Здесь и далее вектора обозначаем жирным шрифтом вместо черточек над буквами

Краевые условия имеют вид:

U∙Y(0) = u,

V∙Y(1) = v,

где

Y(0) – значение искомой вектор-функции на левом крае х=0 размерности 8х1, U – прямоугольная горизонтальная матрица коэффициентов краевых условий левого края размерности 4х8, u – вектор внешних воздействий на левый край размерности 4х1,

Y(1) – значение искомой вектор-функции на правом крае х=1 размерности 8х1, V – прямоугольная горизонтальная матрица коэффициентов краевых условий правого края размерности 4х8, v – вектор внешних воздействий на правый край размерности 4х1.

В случае, когда система дифференциальных уравнений имеет матрицу с постоянными коэффициентами A=const, решение задачи Коши имеет вид (Гантмахер):

Y(x) = e∙ Y(x) + e∙ e∙ F(t) dt,

где

e= E + A(x-x) + A (x-x)/2! + A (x-x)/3! + …,

где E это единичная матрица.

Матричная экспонента ещё может называться матрицей Коши или матрициантом и может обозначаться в виде:

K(x←x) = K(x - x) = e.

Тогда решение задачи Коши может быть записано в виде:

Y(x) = K(x←x) ∙ Y(x) + Y*(x←x) ,

где Y*(x←x) = e∙ e∙ F(t) dt это вектор частного решения неоднородной системы дифференциальных уравнений.

2 Случай переменных коэффициентов

Этот вариант рассмотрения переменных коэффициентов проверялся в кандидатской диссертации.

Из теории матриц (Гантмахер) известно свойство перемножаемости матричных экспонент (матриц Коши):

e= e∙ e ∙ … ∙ e ∙ e,

K(x←x) = K(x←x) ∙ K(x←x) ∙ … ∙ K(x←x) ∙ K(x←x).

В случае, когда система дифференциальных уравнений имеет матрицу с переменными коэффициентами A=A(x), решение задачи Коши предлагается искать при помощи свойства перемножаемости матриц Коши. То есть интервал интегрирования разбивается на малые участки и на малых участках матрицы Коши приближенно вычисляются по формуле для постоянной матрицы в экспоненте. А затем матрицы Коши, вычисленные на малых участках, перемножаются:

K(x←x) = K(x←x) ∙ K(x←x) ∙ … ∙ K(x←x) ∙ K(x←x),

где матрицы Коши приближенно вычисляются по формуле:

K(x←x) = e, где ∆x= x- x.

3 Формула для вычисления вектора частного решения неоднородной системы дифференциальных уравнений

Эта очень простая формула еще не обсчитана на компьютерах. Вместо неё обсчитывалась значительно ранее выведенная и гораздо более сложная формула, приведенная в:

Численный метод переноса краевых условий для жестких дифференциальных уравнений строительной механики Журнал "ММ", Том: 14 (2002), Номер: 9, 3 стр. 1409-003r.pdf

Вместо формулы для вычисления вектора частного решения неоднородной системы дифференциальных уравнений в виде (Гантмахер):

Y*(x←x) = e∙ e∙ F(t) dt

предлагается использовать следующую формулу для каждого отдельного участка интервала интегрирования и тогда вектор частного решения на всем интервале будет складываться из векторов, вычисленных по формуле:

Y*(x←x) = Y*(x- x) = K(x- x) ∙K(x- t) ∙ F(t) dt .

Правильность приведенной формулы подтверждается следующим:

Y*(x- x) = e∙e∙ F(t) dt ,

Y*(x- x) = e∙e∙ F(t) dt ,

Y*(x- x) = e∙ F(t) dt ,

Y*(x- x) = e∙ F(t) dt ,

Y*(x- x) = e∙ e∙ F(t) dt ,

Y*(x←x) = e∙ e∙ F(t) dt,

что и требовалось подтвердить.

Вычисление вектора частного решения системы дифференциальных уравнений производиться при помощи представления матрицы Коши под знаком интеграла в виде ряда и интегрирования этого ряда поэлементно:

Y*(x←x) = Y*(x- x) = K(x- x) ∙K(x- t) ∙ F(t) dt =

= K(x- x) ∙ (E + A(x- t) + A (x- t)/2! + … ) ∙ F(t) dt =

= K(x- x) ∙ (EF(t) dt + A∙(x- t) ∙ F(t) dt + A/2! ∙(x- t) ∙ F(t) dt + … ) .

Эта формула справедлива для случая системы дифференциальных уравнений с постоянной матрицей коэффициентов A=const.

Для случая переменных коэффициентов A=A(x) можно использовать прием разделения участка (x- x) интервала интегрирования на малые подучастки, где на подучастках коэффициенты можно считать постоянными A(x)=const и тогда вектор частного решения неоднородной системы дифференциальных уравнений Y*(x←x) будет на участке складываться из соответствующих векторов подучастков, на которых матрицы Коши приближенно вычисляются при помощи формул с постоянными матрицами в экспонентах.

4 Метод «переноса краевых условий» в произвольную точку интервала интегрирования

Метод обсчитан на компьютерах. По нему уже сделано 3 кандидатских физ-мат диссертации.

Метод подходит для любых краевых задач. А для «жестких» краевых задач показано, что метод считает быстрее, чем метод С.К.Годунова до 2-х порядков (в 100 раз), а для некоторых «жестких» краевых задач не требует ортонормирования вовсе. Смотри:

Численный метод переноса краевых условий для жестких дифференциальных уравнений строительной механики
Журнал "ММ", Том: 14 (2002), Номер: 9, 3 стр. 1409-003r.pdf

Полное решение системы дифференциальных уравнений имеет вид

Y(x) = K(x←x) ∙ Y(x) + Y*(x←x) .

Или можно записать:

Y(0) = K(0←x) ∙ Y(x) + Y*(0←x) .

Подставляем это выражение для Y(0) в краевые условия левого края и получаем:

U∙Y(0) = u,

U∙( K(0←x) ∙ Y(x) + Y*(0←x) ) = u,

( U∙ K(0←x) ) ∙ Y(x) = u - U∙Y*(0←x) .

Или получаем краевые условия, перенесенные в точку x:

U∙ Y(x) = u ,

где U= ( U∙ K(0←x) ) и u = u - U∙Y*(0←x) .

Далее запишем аналогично

Y(x) = K(x←x) ∙ Y(x) + Y*(x←x)

И подставим это выражение для Y(x) в перенесенные краевые условия точки x

U∙ Y(x) = u,

U∙ ( K(x←x) ∙ Y(x) + Y*(x←x) ) = u ,

( U∙ K(x←x) ) ∙ Y(x) = u - U∙ Y*(x←x) ,

Или получаем краевые условия, перенесенные в точку x:

U∙ Y(x) = u ,

где U= ( U∙ K(x←x) ) и u = u - U∙ Y*(x←x) .

И так в точку x переносим матричное краевое условие с левого края и таким же образом переносим матричное краевое условие с правого края и получаем:

U∙ Y(x) = u ,

V∙ Y(x) = v .

Из этих двух матричных уравнений с прямоугольными горизонтальными матрицами коэффициентов очевидно получаем одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов:

∙ Y(x) = .

А в случае «жестких» дифференциальных уравнений предлагается применять построчное ортонормирование матричных краевых условий в процессе их переноса в рассматриваемую точку. Для этого формулы ортонормирования систем линейных алгебраических уравнений можно взять в (Березин, Жидков).

То есть, получив

U∙ Y(x) = u,

применяем к этой группе линейных алгебраических уравнений построчное ортонормирование и получаем эквивалентное матричное краевое условие:

U∙ Y(x) = u.

И теперь уже в это проортонормированное построчно уравнение подставляем

Y(x) = K(x←x) ∙ Y(x) + Y*(x←x) .

И получаем

U∙ ( K(x←x) ∙ Y(x) + Y*(x←x) ) = u ,

( U∙ K(x←x) ) ∙ Y(x) = u - U∙ Y*(x←x) ,

Или получаем краевые условия, перенесенные в точку x:

U∙ Y(x) = u ,

где U= ( U∙ K(x←x) ) и u = u - U∙ Y*(x←x) .

Теперь уже к этой группе линейных алгебраических уравнений применяем построчное ортонормирование и получаем эквивалентное матричное краевое условие:

U∙ Y(x) = u.

И так далее.

И аналогично поступаем с промежуточными матричными краевыми условиями, переносимыми с правого края в рассматриваемую точку.

В итоге получаем систему линейных алгебраических уравнений с квадратной матрицей коэффициентов, состоящую из двух независимо друг от друга поэтапно проортонормированных матричных краевых условий, которая решается любым известным методом для получения решения Y(x) в рассматриваемой точке x:

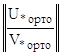∙ Y(x) = .

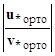5 Второй вариант метода «переноса краевых условий» в произвольную точку интервала интегрирования

Этот вариант метода еще не обсчитан на компьютерах.

Предложено выполнять интегрирование по формулам теории матриц (Гантмахер) сразу от некоторой внутренней точки интервала интегрирования к краям:

Y(0) = K(0←x) ∙ Y(x) + Y*(0←x) ,

Y(1) = K(1←x) ∙ Y(x) + Y*(1←x) .

Подставим эти формулы в краевые условия и получим:

U∙Y(0) = u,

U∙( K(0←x) ∙ Y(x) + Y*(0←x) ) = u,

( U∙ K(0←x) ) ∙ Y(x) = u - U∙Y*(0←x) .

и

V∙Y(1) = v,

V∙( K(1←x) ∙ Y(x) + Y*(1←x) ) = v,

( V∙ K(1←x) ) ∙ Y(x) = v - V∙Y*(1←x) .

То есть получаем два матричных уравнения краевых условий, перенесенные в рассматриваемую точку x:

( U∙ K(0←x) ) ∙ Y(x) = u - U∙Y*(0←x) ,

( V∙ K(1←x) ) ∙ Y(x) = v - V∙Y*(1←x) .

Эти уравнения аналогично объединяются в одну систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения решения Y(x) в любой рассматриваемой точке x:

∙ Y(x) = .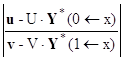

В случае «жестких» дифференциальных уравнений предлагается следующий алгоритм.

Используем свойство перемножаемости матриц Коши:

K(x←x) = K(x←x) ∙ K(x←x) ∙ … ∙ K(x←x) ∙ K(x←x)

и запишем выражения для матриц Коши, например, в виде:

K(0←x) = K(0←x) ∙ K(x←x) ∙ K(x←x),

K(1←x) = K(1←x) ∙ K(x←x) ∙ K(x←x) ∙ K(x←x),

Тогда перенесенные краевые условия можно записать в виде:

( U∙ K(0←x) ∙ K(x←x) ∙ K(x←x) ) ∙ Y(x) = u - U∙Y*(0←x) ,

( V∙ K(1←x) ∙ K(x←x) ∙ K(x←x) ∙ K(x←x) ) ∙ Y(x) = v - V∙Y*(1←x)

или в виде:

( U∙ K(0←x) ∙ K(x←x) ∙ K(x←x) ) ∙ Y(x) = u* ,

( V∙ K(1←x) ∙ K(x←x) ∙ K(x←x) ∙ K(x←x) ) ∙ Y(x) = v* .

Тогда рассмотрим левое перенесенное краевое условие:

( U∙ K(0←x) ∙ K(x←x) ∙ K(x←x) ) ∙ Y(x) = u* ,

( U∙ K(0←x) ) ∙ { K(x←x) ∙ K(x←x) ∙ Y(x) } = u* ,

( матрица ) ∙ { вектор } = вектор .

Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки (матрицы) ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

( U∙ K(0←x) ) ∙ { K(x←x) ∙ K(x←x) ∙ Y(x) } = u* .

Далее последовательно можно записать:

(( U∙ K(0←x) ) ∙ K(x←x) ) ∙ { K(x←x) ∙ Y(x) } = u* ,

( матрица ) ∙ { вектор } = вектор .

Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки (матрицы) ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

(( U∙ K(0←x) ) ∙ K(x←x) ) ∙ { K(x←x) ∙ Y(x) } = u* ,

Далее аналогично можно записать:

((( U∙ K(0←x) ) ∙ K(x←x) ) ∙ K(x←x) ) ∙ { Y(x) } = u* ,

( матрица ) ∙ { вектор} = вектор .

Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки (матрицы) ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

((( U∙ K(0←x) ) ∙ K(x←x) ) ∙ K(x←x) ) ∙ Y(x) = u* .

Аналогично можно проортонормировать матричное уравнение краевых условий и для правого края независимо от левого края.

Далее проортонормированные уравнения краевых условий:

( U∙ K(0←x) ) ∙ Y(x) = u* ,

( V∙ K(1←x) ) ∙ Y(x) = v*

как и ранее объединяются в одну обычную систему линейных алгебраических уравнений с квадратной матрицей коэффициентов для нахождения искомого вектора Y(x) :

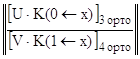∙ Y(x) = .

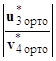6 Метод дополнительных краевых условий

Этот метод еще не обсчитан на компьютерах.

Запишем на левом крае ещё одно уравнение краевых условий:

M ∙ Y(0) = m .

В качестве строк матрицы M можно взять те краевые условия, то есть выражения тех физических параметров, которые не входят в параметры краевых условий левого края L или линейно независимы с ними. Это вполне возможно, так как у краевых задач столько независимых физических параметров какова размерность задачи, а в параметры краевых условий входит только половина физических параметров задачи. То есть, например, если рассматривается задача об оболочке ракеты, то на левом крае могут быть заданы 4 перемещения. Тогда для матрицы М можно взять параметры сил и моментов, которых тоже 4, так как полная размерность такой задачи – 8. Вектор m правой части неизвестен и его надо найти и тогда можно считать, что краевая задача решена, то есть сведена к задаче Коши, то есть найден вектор Y(0) из выражения:

∙ Y(0) = ,

то есть вектор Y(0) находится из решения системы линейных алгебраических уравнений с квадратной невырожденной матрицей коэффициентов, состоящей из блоков U и M.

Аналогично запишем на правом крае ещё одно уравнение краевых условий:

N ∙ Y(0) = n ,

где матрица N записывается из тех же соображений дополнительных линейно независимых параметров на правом крае, а вектор n неизвестен.

Для правого края тоже справедлива соответствующая система уравнений:

∙ Y(1) = .

Запишем Y(1) = K(1←0) ∙Y(0) + Y*(1←0) и подставим в последнюю систему линейных алгебраических уравнений:

∙ ( K(1←0) ∙Y(0) + Y*(1←0) ) = ,

∙ K(1←0) ∙Y(0) = - ∙ Y*(1←0),

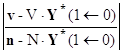∙ K(1←0) ∙Y(0) = ,

∙ K(1←0) ∙Y(0) = .

Запишем вектор Y(0) через обратную матрицу:

Y(0) = ∙

и подставим в предыдущую формулу:

∙ K(1←0) ∙ ∙ = .

Таким образом, мы получили систему уравнений вида:

В ∙ = ,

где матрица В известна, векторы u и s известны, а векторы m и t неизвестны.

Разобьем матрицу В на естественные для нашего случая 4 блока и получим:

∙ = ,

откуда можем записать, что

В11 ∙ u + B12 ∙ m = s,

B21 ∙ u + B22 ∙ m = t.

Следовательно, искомый вектор m вычисляется по формуле:

m = B12 ∙ (s – B11∙ u).

А искомый вектор n вычисляется через вектор t:

t = B21 ∙ u + B22 ∙ m,

n = t + N ∙ Y*(1←0).

В случае «жестких» дифференциальных уравнений предлагается выполнять поочередное построчное ортонормирование.

Запишем приведенную выше формулу

∙ K(1←0) ∙ ∙ =

в виде:

∙ K(1←x2) ∙ K(x2←x1) ∙ K(x1←0) ∙ ∙ = .

Эту формулу можно записать в виде разделения левой части на произведение матрицы на вектор:

( ∙ K(1←x2) ) ∙ { K(x2←x1) ∙ K(x1←0) ∙ ∙ } =

( матрица ) ∙ { вектор } = вектор

Эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки (матрицы) ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

( ∙ K(1←x2) ) { K(x2←x1) ∙ K(x1←0) ∙ ∙ } =

Здесь следует сказать, что подвектор t подвергать преобразованию не нужно, так как невозможно, так как его первоначальное значение не известно. Но подвектор t нам оказывается и не нужен для решения задачи.

Далее запишем:

(( ∙ K(1←x2) ) ∙ K(x2←x1)) { K(x1←0) ∙ ∙ } =

( матрица ) { вектор } = вектор

Аналогично и эту группу линейных алгебраических уравнений можно подвергнуть построчному ортонормированию, которое сделает строчки (матрицы) ортонормированными, {вектор} затронут не будет, а вектор получит преобразование. То есть получим:

(( ∙ K(1←x2) ) K(x2←x1)) { K(x1←0) ∙ } = .

И так далее.

В результате поочередного ортонормирования получим:

В ∙ = ,

∙ = .

Следовательно, искомый вектор m вычисляется по формуле:

m = B12 ∙ (s – B11∙ u).

7 Формула для начала счета методом прогонки С.К.Годунова

Эта формула обсчитана на компьютерах в кандидатской диссертации.

Рассмотрим проблему метода прогонки С.К.Годунова.

редположим, что рассматривается оболочка ракеты. Это тонкостенная труба. Тогда система линейных обыкновенных дифференциальных уравнений будет 8-го порядка, матрица A(x) коэффициентов будет иметь размерность 8х8, искомая вектор-функция Y(x) будет иметь размерность 8х1, а матрицы краевых условий будут прямоугольными горизонтальными размерности 4х8.

Тогда в методе прогонки С.К.Годунова для такой задачи решение ищется в следующем виде:

Y(x) = Y(x) c + Y(x) c + Y(x) c + Y(x) c + Y*(x),

или можно записать в матричном виде:

Y(x) = Y(x) ∙ c + Y*(x),

где векторы Y(x), Y(x), Y(x), Y(x) – это линейно независимые вектора-решения однородной системы дифференциальных уравнений, а вектор Y*(x) – это вектор частного решения неоднородной системы дифференциальных уравнений.

Здесь Y(x)=|| Y(x), Y(x), Y(x), Y(x) || это матрица размерности 8х4, а c это соответствующий вектор размерности 4х1из искомых констант c,c,c,c.

Но вообще то решение для такой краевой задачи с размерностью 8 (вне рамок метода прогонки С.К.Годунова) может состоять не из 4 линейно независимых векторов Y(x), а полностью из всех 8 линейно независимых векторов-решений однородной системы дифференциальных уравнений:

Y(x)=Y(x)c+Y(x)c+Y(x)c+Y(x)c+

+Y(x)c+Y(x)c+Y(x)c+Y(x)c+Y*(x),

И как раз трудность и проблема метода прогонки С.К.Годунова и состоит в том, что решение ищется только с половиной возможных векторов и констант и проблема в том, что такое решение с половиной констант должно удовлетворять условиям на левом крае (стартовом для прогонки) при всех возможных значениях констант, чтобы потом найти эти константы из условий на правом крае.

То есть в методе прогонки С.К.Годунова есть проблема нахождения таких начальных значений Y(0), Y(0), Y(0), Y(0), Y*(0) векторов Y(x), Y(x), Y(x), Y(x), Y*(x), чтобы можно было начать прогонку с левого края x=0, то есть чтобы удовлетворялись условия U∙Y(0) = u на левом крае при любых значениях констант c,c,c,c.

Обычно эта трудность «преодолевается» тем, что дифференциальные уравнения записываются не через функционалы, а через физические параметры и рассматриваются самые простейшие условия на простейшие физические параметры, чтобы начальные значения Y(0), Y(0), Y(0), Y(0), Y*(0) можно было угадать. То есть задачи со сложными краевыми условиями так решать нельзя: например, задачи с упругими условиями на краях.

Ниже предлагается формула для начала вычислений методом прогонки С.К.Годунова.

Выполним построчное ортонормирование матричного уравнения краевых условий на левом крае:

U∙Y(0) = u,

где матрица U прямоугольная и горизонтальная размерности 4х8.

В результате получим эквивалентное уравнение краевых условий на левом крае, но уже с прямоугольной горизонтальной матрицей U размерности 4х8, у которой будут 4 ортонормированные строки:

U∙Y(0) = u,

где в результате ортонормирования вектор u преобразован в вектор u.

Как выполнять построчное ортонормирование систем линейных алгебраических уравнений можно посмотреть в (Березин, Жидков).

Дополним прямоугольную горизонтальную матрицу U до квадратной невырожденной матрицы W:

W = ,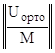

где матрица М размерности 4х8 должна достраивать матрицу U до невырожденной квадратной матрицы W размерности 8х8.

В качестве строк матрицы М можно взять те краевые условия, то есть выражения тех физических параметров, которые не входят в параметры левого края или линейно независимы с ними. Это вполне возможно, так как у краевых задач столько независимых физических параметров какова размерность задачи, то есть в данном случае их 8 штук и если 4 заданы на левом крае, то ещё 4 можно взять с правого края.

Завершим ортонормирование построенной матрицы W, то есть выполним построчное ортонормирование и получим матрицу W размерности 8х8 с ортонормированными строками:

W = .

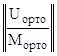Можем записать, что

Y(0) = (М)транспонированная = М.

Тогда, подставив в формулу метода прогонки С.К.Годунова, получим:

Y(0) = Y(0) ∙с + Y*(0)

или

Y(0) = М∙с + Y*(0).

Подставим эту последнюю формулу в краевые условия U∙Y(0) = u и получим:

U∙ ( М∙с + Y*(0) )= u.

Отсюда получаем, что на левом крае константы c уже не на что не влияют, так как

U∙ М = 0 и остается только найти Y*(0) из выражения:

U∙ Y*(0) = u.

Но матрица U имеет размерность 4х8 и её надо дополнить до квадратной невырожденной, чтобы найти вектор Y*(0) из решения соответствующей системы линейных алгебраических уравнений:

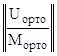∙ Y*(0) = ,

где 0 – любой вектор, в том числе вектор из нулей.

Отсюда получаем при помощи обратной матрицы:

Y*(0) = ∙ ,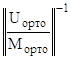

Тогда итоговая формула для начала вычислений методом прогонки С.К.Годунова имеет вид:

Y(0) = М∙с + ∙ .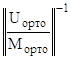

8 Второй алгоритм для н