Математическое моделирование роста доходности страховой компании
Страхование - одна из древнейших категорий общественных отношений и видов деятельности. Зародившись в период разложения первобытно - общественного строя, оно постепенно стало непременным спутником общественного производства. Идея страхования заключается в солидарной замкнутой раскладке ущерба. Сущность страхования состоит в формировании определенного денежного (страхового) фонда и его распределении во времени и пространстве с целью возмещения возможного ущерба (убытков) его участникам при наступлении несчастных случаев, стихийных бедствий и других обстоятельств, приводящих к потере различных видов собственности и активов, предусмотренных договором страхования. Таким образом перераспределительные отношения, присущие страхованию, связаны, с одной стороны, с формированием страхового фонда с помощью заранее зафиксированных страховых платежей, с другой с возмещением ущерба из этого фонда участникам страхования. Специфичность финансовых отношений при страховании состоит в вероятностном характере этих отношений.
Страхование как защита имущественных интересов граждан, организаций и государства является необходимым элементом социально - экономической системы общества. Страхование предоставляет гарантии восстановления нарушенных имущественных интересов в случае непредвиденных природных, техногенных и других явлений, оказывает позитивное влияние на укрепление финансов государства.
Продолжают создаваться крупные страховые компании, способные адаптироваться к динамично меняющейся конъюктуре рынка. Но тем не менее весь объём страховых взносов в нашей стране сопоставим с аналогичными показателями лишь одной западной компании, замыкающей перечень ста крупнейших страховых компаний мира. Финансовые возможности национальных страховых компаний по покрытию крупных убытков остаются низкими. У большинства из них вкладами в уставной капитал являются права на имущество, другие низколиквидные средства, что не лучшим образом влияет на надежность и платёжеспособность страховых компаний.
В настоящее время на территории России страхование осуществляют около 2300 страховых компаний, внесённых в государственный реестр. Как и в других странах, страховое дело в России представлено множеством различных по масштабам и формам организации страховых обществ. По характеру страховых операций все фирмы, функционирующие на страховом рынке, можно разделить на две группы независимо от их организационно-правовой формы.
Первая - универсальные страховщики, которые ориентируются на оказание широкого спектра страховых услуг, осуществляют “все виды деятельности”. У таких компаний наиболее распространено следующее страхование: жизни, от несчастных случаев, медицинское, имущества, грузов, наземного транспорта.
Вторая группа - страховые общества, специализирующиеся на определенном виде страхования ( например, общества медицинского страхования).
Эффективность работы страховых компаний в значительной степени зависит от эффективности работы их организационных служб и от успешности деятельности страховых агентов. Одним из факторов, обеспечивающих выявление путей совершенствования этой деятельности является применение математических методов. В известной литературе по этой проблеме, смотри например (1,4,5,8,10), рассматривают конкретные виды страхования либо проблему автоматизации их собственной деятельности.(3,7,2)
Важнейшей проблемой успешной жизнедеятельности страховых компаний является ее выживание. Проблема выживания многоаспектна. В русле ее решения находятся исследования эффективной тарифной, кредитной, банковской, рекламной, информационной политике и т.д. Некоторые из этих аспектов рассмотрены в литературе и находятся под пристальным вниманием страховых компаний.(9) Однако с нашей точки зрения два направления требуют внимания. Речь идет, во-первых, о совершенствовании работы с физическими лицами, так как именно их средства являются основой поступления надежного денежного потока. Во-вторых, о совершенствовании работы страховых агентов. Это направление требует в настоящее время особого внимания в силу малых средств у физических лиц и появившихся свидетельств неполной заинтересованности отдельных страховых агентов в работе страховых компаний. В связи с этим весьма актуальной является задача выявления таких способов и правил работы страховых агентов, при которых его интересы в большей степени соответствовали интересам фирмы.
В связи со сказанным выше в данной дипломной работе рассматриваются математические модели и методы реализации этих двух направлений. Дипломная работа состоит из 3 глав, приложения, литературы и заключения.
Глава 1. Математическое моделирование роста доходности страховых компаний
§1 Общая характеристика основных фактов и понятий при моделировании деятельности страховых компаний
Рассматривается страховая компания, в которой имеются две группы сотрудников:
· штатные сотрудники (бухгалтера, управленческий персонал и т.д.)
· сотрудники работающие по контракту (страховые агенты)
Затраты по оплате труда штатных сотрудников считаются известными. Общие принципы оплаты труда работников по контракту тоже.
Будем рассматривать всех страховых агентов в объединенной группе, политика выплат администрации относительно каждого из элементов группы одинакова. Эту группу впредь будем называть обобщенным страховым агентом (ОбщСтрахА).
Оплата труда штатных сотрудников осуществляется за счет их собственной деятельности и работы обобщенного страхового агента. Рассмотрим ситуацию, когда деятельность штатных сотрудников оплачивается на основе результатов работы обобщенного страхового агента.
ОбщСтрахА не физическое лицо, а некоторая их совокупность, которая образует динамически стабильную структуру в системе сложившихся экономических отношений внутри страховой компании. Эта группа может рассматриваться в виде относительно независимой ассоциации, поскольку исполняет определенную функцию и в определенных правилах, сформулированных администрацией страховой компании.
Доход страховых агентов складывается из комиссионных вознаграждений за заключенные им договора. Также страховые агенты, как и штатные сотрудники, имеют право на оплачиваемый отпуск, получают премии.
Страховая компания работает на принципе самоокупаемости, осуществляя свои расходы за счет собственных доходов. Основным источником дохода страховых компаний являются страховые взносы ( поступления ). В распоряжении компании имеются следующие виды капиталов: уставной фонд, добавочный капитал, резервный капитал, фонд социальной сферы, фонд накопления, резерв незаработанной премии и другие. Все виды капиталов кроме уставного относятся к оборотному капиталу. Из страховых взносов формируются все необходимые капиталы и фонды, относящиеся к оборотному капиталу. Резервный капитал используется, если расходы на страховое возмещение превышают размер капитала, отведенного на покрытие этих расходов. Он пополняется за счет доходов по инвестициям ( покупка акций, облигаций, вложение средств в банки и т.д.)
Расходы страховой компании включают в себя затраты по заключению договоров страхования, административные расходы (премии страховым агентам, зарплата штатным сотрудникам и другие виды расходов), управленческие расходы (амортизация основных средств, расходы на создание основных фондов, налоги, сборы, затраты на рекламу, затраты на аренду и т.д.).
Все компании предлагают практически одни и те же услуги. Любой страховой продукт, независимо от видов страхования, строится по единой схеме. Каждая страховая услуга включает в себя:
1. технические характеристики - описание рисков и объектов страхования;
2. юридические условия - набор правовых условий, определяющих существо гарантии или ответственности страховщика, оговорки, исключения, особые условия, условия внесения страховой премии и выплаты возмещения;
3. экономические условия - цены, страховые суммы, размер франшиз, индексации и т.д.;
4. дополнительные услуги и сервис, предоставляемые страховщиком;
В процессе заключения договоров страхования страховщик и страхователь определяют и согласовывают необходимые его условия ( все выше перечисленные ). Страховщик при этом стремится, чтобы условия договора обеспечили бы полное и своевременное выполнение им принимаемой на себя ответственности. Страхователь заинтересован в получении полномасштабной страховой защиты при минимизации затрат на нее.
В период смены экономического уклада сложившиеся отношения между страховыми агентами и компанией перестают быть эффективными, так как интересы агента могут выступать в противоречии с интересами страховой компании. Бывают случаи, когда агент заключает заведомо невыгодные договора страхования: страхуют уже разбитую машину, датируя договор задним числом. В связи с этим формируется следующая задача.
Задача: отыскать способы, процедуры оплаты работы страховых агентов, при которых интересы последних и страховых компаний в целом наилучшим образом сочетались бы, и разработать справочник для страхователей и страховщиков, в котором страхователи получили бы полную необходимую им информацию об услугах и правилах страхования, а страховщик всю необходимую справочную информацию о совершенствовании собственной деятельности.
Поставленная выше задача предполагает необходимость решения двух следующих подзадач:
1) задачи сопряжения интересов страховых агентов и страховых компаний;
2) задачи разработки Справочника страховщика и страхователя;
Математическое описание моделей, обеспечивающих решение первой подзадачи приведено в §2 главы 1. Качественный математический анализ разработанных моделей, способы сведения их к оптимизационным задачам стандартного вида и программный комплекс реализации алгоритмов описаны в главе 2. Постановка и решение задачи формирования Справочника приведены в главе 3.
§2 Математические модели роста доходности страховых компаний
Математические модели выживания страховых компаний на основе оптимизации деятельности страховых агентов формулируется как задачи оптимального управления с коэффициентами, характеризующими долю участия агента в суммарном доходе страховой компании. При этом формулируется простейший алгоритм модели, в которой по отношению ко всем страховым агентам проводится единая политика их заинтересованности, и два более сложных аналога (многомерный и многосекторный). В многомерном при описании модели предполагается, что политика администрации компании по отношению к страховым не одинакова и оплата труда страховых агентов производится дифференцировано с учетом их участка работы, оборотный капитал компании складывается как сумма капиталов, заработанных каждым агентом.
В многосекторной аналоге предполагается, что страховая компания является неспециализированной, доходность страховой компании есть сумма частей, принесенных каждым страховым агентом.
п.1 Формулировка простейшей модели роста доходности страховых компаний.
При формулировке этой модели используется идея работы Яновского Л.П. (14), переписывается в условиях новой сферы и модифицируется в следствие новых условий.
Пусть I(t) - доход обобщенного страхового агента, R(t) - доходность страховой компании (объем поступивших страховых платежей), a - весовой коэффициент,0 Тогда целевой функционал модели, характеризующий суммарный специальным образом рассчитанный доход страховой компании может быть записан в следующем виде: ? J(t)=ò(aI(t)+(1-a)R(t))e-rt dt ® max 0 Здесь e-rt- функция дисконтирования; r - коэффициент дисконтирования. Заметим, что доходность страховой компании, мы будем рассматривать как функцию от оборотного капитала (K(t)) и фонда оплаты труда штатных сотрудников (L(t)). R(t)=F(k(t),L(t)) (2.1) Отметим, что обобщенный страховой агент не входят в число штатных сотрудников, а работает на основе контракта. Его доход I(t)) определяется как доля от величины поступивших за счет его работы страховых платежей. При этом, если представить, что работа обобщенного страхового агента является единственным источником дохода страховой компании, а ставка комиссионного вознаграждения (m) известна, тогда справедливо соотношение. I(t)=mR(t), 0 Полученный доход R(t) используется по следующим направлениям: · формирование дохода обобщенного страхового агента: mR(t) · развитие жизнедеятельности фирмы (1-m)R(t)=Wa(t)+L(t)+K’(t)+dK(t)+p(t)K(t) p(t)³pc, p(t)- прибыль держателей акций Wa(t) - затраты, связанные с процессом и обслуживанием заключения договоров страхования и средств, выделяемых администрацией обобщенному страховому агенту в форме отпускных и других положенных ему денежных вознаграждений Wa(t) = gK(t)+CmL(t) Здесь g - доля капитала, отведенная на покрытие расходов, связанных с процессом и обслуживанием заключения договоров страхования, 0 Таким образом, простейшая модель записывается ввиде ? -rt J(t)=ò(aI(t)+(1-a)R(t))e dt 0 R(t)=F(K(t),L(t)) I(t)=mR(t) (1-m)R(t)=Wa(t)+L(t)+K’(t)+dK(t)+p(t)K(t) p(t)³pc, 0 Wa(t) = gK(t)+CmL(t) 0 L(0)=L0, L0>0, K(0)=K0, K0>0 L0, K0-фиксированы Модель представляет собой задачу оптимального управления с параметрами управления a,g,m,d,Сm. n2. Многомерная модель роста доходности страховой компании. Рассматривается страховая фирма, в которой работают n страховых агентов. Каждый агент работает на своем участке. Участки считаются неэквивалентными. Для того чтобы оценить работу страхового агента, введем коэффициент b, который зависит от следующих факторов: 1.плотность населения участка 2. уровень доходности жителей и т.д. 3. тип района, где расположен участок 4. опыт работы страхового агента Обозначим коэффициент каждого агента bi,где i=1,n и Предположим, что капитал фирмы есть сумма капиталов, заработанных каждым агентом. K(t)=åKj(t) (2.2) j=1 Предположим, что оплата труда организационных работников осуществляется за счет работы страховых агентов и затраты на их содержание распределяются пропорционально между всеми агентами. Как и в модели рассмотренной выше, нас интересует ситуация, когда интересы, заключающиеся в получении максимума прибыли, агента и компании взаимосвязаны. В силу аналогичных рассуждений целевой функционал построим в виде: ¥ n J(t)=ò( åaIj(t) +(1-a)R(t))e-rt dt 0 j=1 здесь Ij(t)- доход j - го агента, "j j=1,n R(t) можно представить в виде производственной функции. Т.е. R(t)=F(K1(t),K2(t),..., Kn(t), L(t)) (2.3) Здесь Kj(t) - капитал, заработанный j - ым агентом. Доход страхового агента можно представить как долю от величины поступивших за счет его работы страховых платежей с учетом коэффициента, характеризующего его страховое поле.(Определения, связанные со страхованием смотри в приложении 1) Все необходимые предположения для определения дохода j-го страхового агента сделаны в п.1 Ij(t)=mbjR(t), где 0 Аналогично рассуждениям, приведенным в предыдущей модели, R(t) используется по тем же направлениям. Часть дохода страховой компании, идущая на развитие жизнедеятельности фирмы, распределяется следующим образом: n (1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t) (2.4) j=1 Здесь Waj(t) - затраты, связанные с процессом и обслуживанием заключения договоров страхования и средств, выделяемых администрацией j - му страховому агенту в форме отпускных и других положенных ему денежных вознаграждений. Waj(t) = gKj(t)+CmL(t)/n "j j=1,n (2.5) Все прочие обозначения смотрите в п.1. Таким образом модель имеет вид: Максимизировать ¥ n J(t)=ò( åaIj(t) +(1-a)R(t))e-rt dt 0 j=1 при условиях n (1-m)R(t)=åWaj(t) +L(t)+dK(t)+ K’(t) +p(t) K(t) j=1 R(t)=F(K1(t),K2(t),..., Kn(t), L(t)) Ij(t)=mbjR(t), где 0 Waj(t) = gKj(t)+CmL(t), "j j=1,n 0 p(t)³pс,0 L(0)=L0, L0>0,K(0)=K0,K0>0 п3. Многосекторная модель роста доходности страховой фирмы. Рассматривается страховая фирма, которая предлагает n видов страхования. Каждый агент занимается только одним видом страхования, таким образом имеем n агентов. Все агенты работают на одном и том же участке. Предполагается, что доходность фирмы складывается из договоров, заключенных агентами, т.е. n R(t)= åRj(t). j=1 Верно также и соотношение (2.2) В силу аналогичных рассуждений целевой функционал построим в виде: ¥ n n J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e-rt dt 0 j=1 j=1 Здесь Ij(t)- доход агента, где j=1,n. Rj(t) - объем заключенных договоров j-ым агентом, в руб. Rj(t) можно представить в виде производственной функции. Rj(t)=F(Kj(t), L(t)), "j j=1,n. (2.6). Из рассуждений приведенных в п.2 доход j - го страхового агента определяется по формуле Ij(t)=mjRj(t), "j j=1,n. Рассуждения, связанные с распределением дохода страховой компании аналогичны приведенным выше. ( п.2). Соответственно сохраняются выражения (2.4) и (2.5). Таким образом многосекторная модель имеет вид Максимизировать ¥ n n J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e -rt dt 0 j=1 j=1 при ограничениях Rj(t)=F(Kj(t), L(t)) "j j=1,n Ij(t)=m jRj(t) "j,j=1,n n (1- m)R(t)= åWaj(t)+L(t)+K’(t)+dK(t)+p(t)K(t) j=1 Waj(t) = gKj(t)+CmL(t) "j,j=1,n 0 0 L(0)=L0, L0>0, K(0)=K0, K0>0 п.4 Дискретный аналог простейшей модели роста доходности. Дискретным аналогом простейшей модели является следующая модель, при постановке которой использовалась идея модели Лурье (6,стр.173) aIT+(1-a)(RT+pcKT) ® max при ограничениях It=mRt-1-haD Kt-1 "t t=1,T Rt=F(Kt,Lt) "t t=1,T Kt=Kt-1+(1-a)D Kt "t t=1,T Lt=Lt-1+D Lt "t t=1,T (1-m)Rt=Wat+Lt+dKt+pcKt "t t=1,T Wat=g Kt+CmLt "t t=1,T 0 K0, L0,а, d,pc,g, Cm- заданы Здесь Т- конец рассматриваемого периода, а- доля выплат в общем потоке поступления средств, h - коэффициент штрафа, DKt-величина поступления оборотного капитала в период t, DLt- величина поступления фонда оплаты труда в период t. Все остальные обозначения смотри в п.1. Глава 2. Математический анализ моделей роста доходности страховой компании §1 Математические анализ модели роста доходности страховой компании Рассмотрим простейший аналог модели, приведенный в §2 главы 1. Приведем ее формулировку: Максимизировать ? ò (aI(t) + (1-a) R(t)) e-rt dt 0 при условии (1-m)R(t)=gK(t)+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K, 0 p(t)³pc,0 L(0)=L0, L0>0 K(0)= K0, K0>0 K0 - начальный капитал фирмы, L0 - начальное значение фонда оплаты труда. Осуществим некоторые упрощения. Предположим, что p(t)=pc. (1.1) Учитывая (2.1) (гл.1) и тот факт, что F(K(t),L(t)) однородна и построив функцию Лагранжа, получим: W(t)=(1- a+am)Lj(K(t)/L(t))e-rt + l(t)( -(1-m)L(t)j(K(t)/L(t)) + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t)) В результате исходная модель приводится к виду: ? ò W(t) dt ®max (1.2) 0 при условиях L(0)=L0, K(0)=K0 (1.3) 0 Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (1.2)-(1.4) e-rt(1-a+am)(j( K’(t)-(1-m)L(t)j( Обозначим k(t)=K(t)/L(t) и продифференцируем по t k’(t)= Из (1.5) учитывая, что n(t)=(dL/dt)/L(t), получим: K’(t)/L(t) = k’(t)+ k (t)n(t) (1.7) ля упрощения выписанных выше выражений введем еще одно обозначение: z(k) = j’(k) k -j(k) (1.8) Функция j(k) построена на основе F( a) j¢(k)>0 b) j¢¢(k)<0 c) j’(k) ® ? для k ® 0 d) j’(k) ® 0 для k ® ? Разделив последнее уравнение из (1.5) на L(t) и учтя обозначения, получим: l’(t)= (1-a+am)j’(k(t))e-rt+l(t)(g+d+pc-(1-m)j’(k(t))) (1.9) l(t) =( 1-a+am)z(k(t))e-rt /((1-m)z(k(t))+Cm+ 1) (1.10) k’(t)=(1-m)j(k(t))-(g+d+pc)k(t)- (Cm+1) (1.11) Продифференцировав (1.10) по t, получим: -rt l¢(t)= Учитывая, что z’(k(t)) =j’’(k(t))k’(t)k(t) (1.13), получаем, что формула (1.12) примет вид. -rt l¢(t)= Подставляя в (1.14) соотношения (1.9) и (1.10), выясним, что темп изменения капиталовооруженности вычисляется по формуле: k’(t) = где U(t) = (1 -m ) z(k(t)) + 1 + Cm V(t) =(1-a+am)(j¢(k(t))U(t) + z(k(t))(r + d+g+pc-(1-m)j¢(k(t))) Проведем качественный анализ уравнения ( 1.15 ). Так как j¢(k) <0 для k >0, знаменатель в ( 1.15 ) отрицателен.(Мы предполагаем, что (1-a+am)(1+Cm)>0). Далее из условий на функцию j(k) для z(k)=j¢(k)k-j(k) получаем z(k)£0 и z(k)® 0 при k ®0, и z(k) ® - ? при к ® ?. Для малых k получаем U>0, V>0, так как j¢(k) - большое число, то k’<0. Для больших k получаем U<0, V<0, так как z(k) ® - ?, следовательно k’ <0. Из монотонного убывания U и V, что каждое из рассматриваемых уравнений U=0 и V=0 имеет единственный корень. Таким образом область разбивается на три участка: kÎ(0,k1), k Î( k1, k2),kÎ( k2,¥) Из рисунка 1 видно, что существует одна точка не устойчивого равновесия k1(m) и две точки 0 и k2(m) устойчивого равновесия. Нетрудно видеть, что k1(m) и k2(a,m) монотонно возрастающие функции по m. Если начальное значение k0=K0/L0 меньше чем k1(m), тогда k® 0 и фирма гибнет. В противном случае размеры фирмы стабилизируются и стремятся к k2(m). Следовательно мы можем рассматривать k2(m) как оптимальный размер фирмы для данных значений параметров управления a,m,g,d,Wr,Cm. Таким образом, если заданы величины указанных выше параметров, то по величине k(t)= Предлагается следующий путь: Если DK(t)®max Если нет никакой возможности по увеличению капитала, то уменьшают фонд оплаты труда. В этом случае задача выглядит следующим образом: L(t)* DL(t)®min Приведем пример расчетов оптимального размера фирмы. Рассмотрим влияние изменений параметра управления a на оптимальный размер страховой компании. Данные для расчета были предоставлены компанией Росгосстрах. Предполагается, что d=0.13, g=0.03, m= 0.1, Cm=0.8. Тогда зависимость k1, k2 представлены в таблице 1. k1 k2 Таб.1 Можно исследовать значения k1 и k2 для других значений параметров, полагая m= 0.05, получаем таблицу 2. k1 k2 Таб.2 Окончательно заметим, что изменение ставки комиссионного вознаграждения m при фиксированном капитале К ведет к уменьшению капиталовооруженности k. §2 Математический анализ многомерной модели роста доходности страховых компаний Рассматриваемая модель имеет вид: Максимизировать при условии (1-m)R(t)= 0 L(0)= L0, L0>0 K(0)= K0,K0>0 K0 - начальный оборотный капитал фирмы, L0 - начальный фонд оплаты труда штатных работников. Будем рассматривать случай для n=2. Тогда рассматриваемая модель примет вид: Максимизировать при условии (1-m)R(t)=g(K1(t)+K2(t))+CmL(t)+L(t)+dK(t)+K’(t)+p(t)K(t), 0 L(0)=L0, L0>0 K(0)= K0, K0>0 Выпишем функцию Лагранжа, учитывая (2.3) (гл.1) для случая n=2,(1.1) и тот факт, что F(K1(t), K2(t),L(t)) однородна, получим: W(t)=(1- a+am(b1+b2))L(t)j l(t)(-(1-m)L(t) j В результате исходная модель примет вид: при условиях L(0)=L0, K(0)=K0 (2.2) 0 Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (2.1)-(2.3) (1-a+am(b1+b2))j’k1/l j’ (1-a+am(b1+b2))j’k2/l l(t)=((1-a+am(b1+b2))( j’ K’(t)-(1-m)L(t)j Перепишем последнюю систему в удобном виде. l’(t)=(1-a+am(b1+b2))j’k1/l l l(t)(g+d+pc-(1-m)j’k1/l l l’(t)=(1-a+am(b1+b2))j’k2/l l l(t)(g+d+pc-(1-m)j’k2/l l l(t)=((1-a+am(b1+b2))( j’ K’(t)=(1-m)L(t)j Обозначим k(t)=K(t)/L(t), k1(t)=K1(t)/L(t), k2(t)=K2(t)/L(t) и n(t)=(dL/dt)/L (2.5) и проведем аналогичные §1 рассуждения. Тогда справедливо соотношение (1.7). Для упрощения полученной системы введем еще одно обозначение: z(k(t)) = j’k1(t)(k1(t),k2(t)) k1(t) +j’k2(t)(k1(t),k2(t)) k2(t)-j(k1(t),k2(t)) Разделив уравнение (2.4) на L(t) и учитывая обозначения, получим: l’(t)=(1-a+am(b1+b2))j’k1(k1(t), k2(t))e-rt+ l(t)(g+d+pc-(1-m)j’k1(k1(t), k2(t))) (2.6) l’(t)=(1-a+am(b1+b2))j’k2(k1(t),k2(t))e-rt+ l(t)(g+d+pc-(1-m)j’k2(k1(t), k2(t))) (2.7) l(t)=((1-a+am(b1+b2))z(k1(t),k2(t))e-rt)/((1-m)(z(k1(t),k2(t))+Cm+1) (2.8) k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1) (2.9) Продифференцируем (2.8) по t. Получим: -rt l¢(t)= Учитывая, что z’(k1(t),k2(t)) =j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t), получаем, что формула (2.10) примет вид l¢(t) =e -rt(j’’k1k1( k1(t),k2(t))k’1(t)k1(t) +j’’k2k2( k1(t),k2(t))k’2(t)k2(t))(1- a+am(b1+b2))(Cm+1) / ((1 -m)z(k1(t),k2(t)) + Cm +1) 2 - rl(t) (2.11) Подставляем в (2.11) соотношения (2.6) и (2.8), (2.7) и (2.8) соответственно, получим, что темп изменения капиталовооруженности вычисляется по формулам: k’(t)=(1-m)j(k1(t),k2(t))-(g+d+pc)k(t)-(Cm+1) k’1(t)= k’2(t)= где U(t)= (1 -m)z(k1(t),k2(t)) + Cm +1 V1(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k1( k1(t),k2(t))(1 -m)-(g+d+pc+r)) V2(t)= Cm +1+z(k1(t),k2(t))((1 -m) +j’k2( k1(t),k2(t))(1 -m)-(g+d+pc+r)) Рассмотрим случай, когда оба агента участвуют в формировании капитала фирмы в равных долях. Тогда (при n=1) рассматриваемая модель сводится к сличаю приведенному в §1. Однако, если доли не равны, то приходим к качественно новой задаче. §3 Математический анализ многосекторной модели роста доходности страховой компании Напишем ее формулировку. Максимизировать ¥ n n -rt J(t)=ò( åaIj(t)+ å(1-a)Rj(t))e dt 0 j=1 j=1 при ограничениях Rj(t)=F(Kj(t), L(t)) "j j=1,n Ij(t)=m jRj(t), 0 n (1- m)R(t)= åWaj(t)+L(t)+K’(t)+dK(t)+p(t)K(t) j=1 Waj(t) = gKj(t)+CmL(t) "j,j=1,n 0 0 L(0)=L0, L0>0, K(0)=K0, K0>0 Выпишем модель для случая n=2. Максимизировать ? ò (a(m1 R1(t) + m1R2(t)) + (1-a) (R1(t)+R(t)) e -rt dt 0 при условии (1-m1-m2)R(t)=g( K1(t)+ K2(t))+ CmL(t)+L(t) + dK(t)+K’(t)+p(t)K(t), 0 L(0)=L0, L0>0 K(0)=K0,K0>0 K0 - начальный капитал фирмы, L0 - начальное количество работников. Выпишем функцию Лагранжа, учитывая (2.6), (1.1) и тот факт, что F(Kî(t),L(t)) "j,j=1,2 однородна, получим: W(t)=(am1L(t)j( ( В результате исходная модель записывается в виде (2.1)-(2.3) Далее, выпишем систему уравнений Эйлера - Лагранжа, вытекающую из (2.1)-(2.3) ( am1j ‘( ( am2j ‘( (a ( m1j( K’(t)-(1-m)L(t)j( Перепишем последнюю систему в удобном виде. l¢(t)=(am1j’( l¢(t)=(am2j’( (am1(j(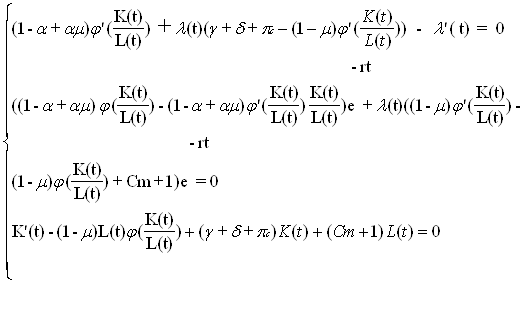
![]() Перепишем последнюю систему в удобном виде.
Перепишем последнюю систему в удобном виде.![]() l¢(t)=(1-a+am)j’(
l¢(t)=(1-a+am)j’(![]() )e-rt+l(t)(g+d+pc-(1-m)j’(
)e-rt+l(t)(g+d+pc-(1-m)j’(![]() )
)![]() )-j’(
)-j’(![]() )
)![]() )+l(t)((1-m)(j’(
)+l(t)((1-m)(j’(![]() )
)![]() -j(
-j(![]() ))+ Cm+1)=0
))+ Cm+1)=0 ![]() )+(g+d+pc)K(t)+(Cm+1)L(t)=0 (1.5)
)+(g+d+pc)K(t)+(Cm+1)L(t)=0 (1.5) ![]() (1.6)
(1.6)![]() ,1) и поэтому для нее выполняются следующие свойства:
,1) и поэтому для нее выполняются следующие свойства:![]() 2 -rl(t) (1.12)
2 -rl(t) (1.12)![]() 2-rl(t) (1.14)
2-rl(t) (1.14)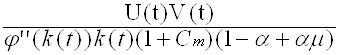 (1.15)
(1.15)![]() может быть оценено качество начального состояния и перспективы развития страховой компании.
может быть оценено качество начального состояния и перспективы развития страховой компании. ![]()
![]() >K(0)
>K(0)![]() >K(0)
>K(0)k/a 0 ¼ 1/2 ¾ 1 7.2 7.2 7.2 7.2 7.2 3.49 3.39 3.15 3.13 2.93 a 0 1/4 1/2 3/4 1 6.8 6.8 6.8 6.8 6.8 3.4 3.23 3.15 3.13 3 ![]() m
m ![]() R(t) + (1-a) R(t)) e-rt dt
R(t) + (1-a) R(t)) e-rt dt ![]() +(Cm+1)L(t) + dK(t)+ K’(t)+ p(t)K,
+(Cm+1)L(t) + dK(t)+ K’(t)+ p(t)K,![]() (am (b1+b2)R(t) + (1-a) R(t)) e -rt dt
(am (b1+b2)R(t) + (1-a) R(t)) e -rt dt ![]() e-rt+
e-rt+![]() + (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))
+ (g+d+pc)K(t) + (Cm + 1)L(t) + K’(t))![]() W(t) dt ® max (2.1)
W(t) dt ® max (2.1) ![]() e-rt+l(t)(g+d+pc-(1-m)
e-rt+l(t)(g+d+pc-(1-m) ![]() )-l’(t)=0
)-l’(t)=0 ![]() )e-rt+l(t)(g+d+pc-(1-m)j’k2/l
)e-rt+l(t)(g+d+pc-(1-m)j’k2/l![]() ) -l’(t)=0
) -l’(t)=0 ![]() j’k1/l
j’k1/l![]() +
+ ![]() j’k2/l
j’k2/l![]() -j
-j![]() +e-rt)/((1-m)(
+e-rt)/((1-m)(![]() j’k1/l
j’k1/l![]() +
+![]()
![]()
![]() -j
-j![]() -Cm-1)
-Cm-1) ![]() +(g+d+pc)K(t)+(Cm+1)L(t)=0
+(g+d+pc)K(t)+(Cm+1)L(t)=0 ![]() )e-rt+
)e-rt+ ![]() )
) ![]() e-rt+
e-rt+ ![]() )
) ![]() j’k1/l
j’k1/l![]() +
+ ![]() j’k2/l
j’k2/l![]() -j
-j![]() +e-rt)/((1-m)(
+e-rt)/((1-m)(![]() j’k1/l
j’k1/l![]() +
+![]()
![]()
![]() -j
-j![]() -Cm-1)
-Cm-1) ![]() -(g+d+pc)K(t)-(Cm+1)L(t) (2.4)
-(g+d+pc)K(t)-(Cm+1)L(t) (2.4)![]() 2 -rl(t) (2.10)
2 -rl(t) (2.10)![]()
![]()
![]() )+am2L(t)j( (
)+am2L(t)j( (![]() )+(1- a)L(t)j( (
)+(1- a)L(t)j( (![]() )e-rt + l(t)( -(1-m1-m2)L(t)j((
)e-rt + l(t)( -(1-m1-m2)L(t)j((![]() ) + (g+d+pc)K(t) + (Cm +1)L(t) + K’(t))
) + (g+d+pc)K(t) + (Cm +1)L(t) + K’(t))![]() ) + (1-a)j’(
) + (1-a)j’(![]() )e-rt+l(t)(g+d+pc-(1-m1-m2)j’(
)e-rt+l(t)(g+d+pc-(1-m1-m2)j’(![]() )-l’(t)=0
)-l’(t)=0 ![]() ) + (1-a)j’(
) + (1-a)j’(![]() )e-rt+l(t)(g+d+pc-(1-m1-m2)j’(
)e-rt+l(t)(g+d+pc-(1-m1-m2)j’(![]() )-l’(t)=0
)-l’(t)=0 ![]() ) +m2j(
) +m2j(![]() )-(m1j’(
)-(m1j’(![]() )
)![]() +m2j’ (
+m2j’ (![]() )
)![]() )) + (1-a) (j(
)) + (1-a) (j(![]() )-j’(
)-j’(![]() )
)![]() ))e -rt+l(t)((1-m1-m2)j’(
))e -rt+l(t)((1-m1-m2)j’(![]() )
)![]() -(1-m1-m2)j(
-(1-m1-m2)j(![]() ) + Cm+1)=0
) + Cm+1)=0 ![]() )+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.1)
)+(g+d+pc)K(t)+(Cm+1 )L(t)=0 (3.1) ![]() )+(1-a)j’(
)+(1-a)j’(![]() ))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((
))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((![]() ))
))![]() )+(1-a)j’(
)+(1-a)j’(![]() ))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((
))e-rt+l(t)(g+d+pc-(1-m1-m2)j’((![]() ))
)) ![]() )-j’(
)-j’(![]() )
)![]() )+am2(j(
)+am2(j(![]() )-j’(
)-j’(
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Математическое моделирование экономических процессов на железнодорожном транспорте
1. ОПТИМИЗАЦИЯ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРЕДПРИЯТИЯ ПО ДЕПОВСКОМУ РЕМОНТУ ГРУЗОВЫХ ВАГОНОВ1.1 Методика решения задачи1.2 Исходные да
- Анализ методов ценообразования на примере ООО "Торгсервис"
Цена играет особую роль в рыночной экономике. В ней, отражается вся система ценообразующих факторов (инфляция, спрос, предложение и др.).
- Анализ платежеспособности и финансовой устойчивости предприятия
- Анализ производительности и оплаты труда
СодержаниеВведение. 21 Теоретические основы оплаты и производительности труда. 81.1 Методика расчета производительности труда. 141.2 Класси
- Анализ производительности труда на предприятиях
- Анализ рентабельности и резервы её роста
- Анализ рынка соков
СодержаниеГлава 1. Общая характеристика рынка1.1. Объем производства1.2. Эластичность спроса1.3. Динамика спроса 1.4. Сырьевая база Глава 2. Ст
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

