Математическое моделирование экономических процессов на железнодорожном транспорте
1. ОПТИМИЗАЦИЯ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ПРЕДПРИЯТИЯ ПО ДЕПОВСКОМУ РЕМОНТУ ГРУЗОВЫХ ВАГОНОВ
1.1 Методика решения задачи
1.2 Исходные данные
1.3 Последовательность решения задачи
2. ОПТИМИЗАЦИЯ ЗАГРУЗКИ МОЩНОСТЕЙ ПО ПРОИЗВОДСТВУ ЗАПАСНЫХ ЧАСТЕЙ ДЛЯ ПРЕДПРИЯТИЙ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
2.1 Постановка задачи
2.2 Методика решения задачи
2.3 Исходные данные
2.4 Последовательность решения задачи
3. ЭКОНОМИКО-МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МЕЖОТРАСЛЕВОГО БАЛАНСА (МОДЕЛЬ «ЗАТРАТЫ–ВЫПУСК»)
3.1 Методика решения задачи
3.2 Исходные данные
3.3 Последовательность решения задачи
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
В современных условиях роль экономико-математических методов и моделей в решении широкого круга экономических и производственных задач существенно возрастает. Это в полной мере относится к железнодорожному транспорту, для которого методология экономико-математического моделирования всегда являлась действенным инструментом повышения эффективности его работы.
В связи с широким внедрением в экономическую практику современных информационных технологий возможности экономико-математического моделирования для решения прикладных задач существенно расширились. В частности средства MICROSOFT EXEL позволяют решать большинство задач, входящих в инструментарий экономико-математического моделирования. В связи с этим в методических указаниях представлены три расчетно-графические работы по экономико-математическому моделированию, отражающих специфику железнодорожного транспорта.
1. ОПТИМИЗАЦИЯ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ВАГОНОРЕМОТНОГО ПРЕДПРИЯТИЯ ПО ДЕПОВСКОМУ РЕМОНТУ ГРУЗОВЫХ ВАГОНОВ
1.1 Методика решения задачи
Деповской ремонт грузовых вагонов выполняется в ремонтных вагонных депо, входящих в Департамент ОАО «РЖД» по ремонту грузового вагонного парка. Программа ремонта по количеству и типам вагонов для каждого депо в отдельности устанавливается департаментом исходя из потребностей в ремонте, производственных мощностей депо и имеющихся в наличии производственных ресурсов. С учетом того, что в настоящее время неуклонно возрастает вагонный парк других собственников, а также предстоящим акционированием Департамента возникает проблема определения оптимальной производственной программы депо, обеспечивающей максимальную прибыль предприятию. Такая задача может быть сформулирована следующим образом. Имеем:
Хi – объем ремонта вагонов j–го типа; i = 1, 2, … n;
Вi – объем, имеющихся в наличии производственных ресурсов i-го вида; I = 1, 2, … m;
aij – расход i-го вида ресурсов на ремонт одного вагона j-го типа;
Cj – прибыль, получаемая предприятием за один отремонтированный вагон j-го типа.
Решение задачи осуществляется на основе следующей экономико-математической модели:
Найти совокупность переменных Хj, минимизирующую целевую функцию F:
![]() (1.1)
(1.1)
На целевую функцию накладываются следующие ограничения:
![]() (1.2)
(1.2)
![]()
![]()
Xij ≥ 0 для всех значений индексов. (1.3)
Данная модель относится к классу экономико-математических моделей линейного программирования (4, 5, 8, 9). Решение задач, описываемых экономико-математическими моделями линейного программирования, как правило, осуществляется универсальным симплексным методом (4, 5).
Он достаточно трудоемок. Поэтому выполнение расчетов рекомендуется в среде EXCEL (2, 7).
Технологию решения задач линейного программирования в среде EXCEL продемонстрируем на следующем примере.
Вагоноремонтное депо имеет в своем распоряжении определенное количество ресурсов: рабочую силу, материалы, запасные части, оборудование, производственные площади и т. п. Допустим, например, имеются ресурсы четырех видов: рабочая сила, материалы, специальные запасные части и фонд времени вагоноремонтных позиций. Депо может ремонтировать вагоны четырех типов. Информация о количестве единиц каждого ресурса, необходимого для ремонта одного вагона каждого типа, их объеме и получаемой прибыли приведена в табл. 1.
Таблица 1.1
| Ресурсы | Нормы расхода ресурсов на один вагон | Наличие ресурсов | |||
| полувагон | крытый | платформа | хопердозатор | ||
| Раб. сила, чел.час | 180 | 205 | 160 | 336 | 650000 |
| Материалы, тыс. руб | 28 | 27 | 26 | 54 | 100000 |
| Фонд времени, час | 17 | 18 | 16 | 30 | 125000 |
Специальные запчасти, тыс. руб. | 0 | 0 | 0 | 15 | 5000 |
| Прибыль на 1 вагон, тыс. руб. | 7,3 | 7,5 | 6,5 | 15 | |
Требуется найти такой план ремонта вагонов, при котором будет максимальной общая прибыль предприятия.
Обозначим через Х1, Х2, Х3, Х4 количество вагонов каждого типа. Сформулируем экономико-математическую модель задачи:
F = 7,3Х1 + 7,5Х2 + 6,5Х3 + 15Х4 à max
180Х1 + 205Х2 + 160Х3 + 336Х4 ≤ 650000,
28Х1 + 27X2 + 26Х3 + 54Х4 ≤ 100000,
17Х1 + 18Х2 + 16Х3 + 30Х 4 ≤ 125000,
15 ∙ Х4 ≤ 5000
X1 ≥ 0; X2 ≥ 0; X3 ≥ 0; X4 ≥ 0
Решение задач линейного программирования в среде EXCEL осуществляется с помощью надстройки «Поиск решения» (2, 7). Если в меню Сервис отсутствует команда Поиск решения, значит, необходимо загрузить эту надстройку. Выберите команду Сервиса Надстройки и активизируйте надстройку Поиск решения. Если же этой надстройки нет в диалоговом окне Надстройки, то необходимо обратиться к панели управления Windows, щелкнуть на пиктограмме Установка и удаление программ и с помощью программы установки EXCEL (или Office) установить надстройку Поиск решения. Для решения задачи необходимо:
1. Создать форму для ввода условий задачи.
2. Указать адреса ячеек, в которые будет помещен результат решения (изменяемые ячейки).
3. Ввести исходные данные.
4. Ввести зависимость для целевой функции.
5. Ввести зависимости для ограничений.
6. Указать назначение целевой функции (установить целевую ячейку).
7. Ввести ограничения.
8. Ввести параметры для решения задачи линейного программирования.
Для рассматриваемого примера продемонстрируем технологию решения задачи оптимального использования ресурсов.
1. Подготовим форму для ввода условий задачи (рис. 1).
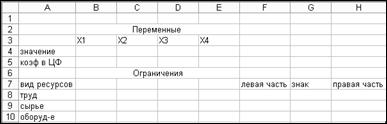
Рис. 1
2. В нашей задаче оптимальные значения вектора X = (Х1, Х2 Х3, Х4) будут помещены в ячейках ВЗ: ЕЗ, оптимальное значение целевой функции - в ячейке F4.![]()
3. Введем исходные данные в созданную форму. Получим результат, показанный на рис. 2.
4.Введем зависимость для целевой функции:
• Курсор в F4.
• Курсор на кнопку Мастер функций.
| Переменные | |||||||
| Х1 | Х2 | Х3 | Х4 | ||||
| Значение | ЦФ | ||||||
| коэф. в ЦФ | 7,3 | 7,5 | 6,5 | 15 | 0 | ||
| Ограничения | |||||||
| Вид ресурсов | Левая часть | Знак | Правая часть | ||||
| Труд | 180 | 205 | 160 | 336 | <= | 650000 | |
| Материалы | 28 | 27 | 26 | 54 | <= | 100000 | |
| Фонд времени | 17 | 18 | 16 | 30 | <= | 125000 | |
| Спец. запчасти | 0 | 0 | 0 | 15 | <= | 5000 | |
Рис.2. Данные введены
M1 (Обозначим через М1 следующее действие – «один щелчок левой кнопкой мыши»). На экране диалоговое окно Мастер функций шаг 1 из 2.
• Курсор в окно Категория на категорию Математические.
• M1.
• Курсор в окно Функции на СУММПРОИЗВ.
• M1.
• В массив 1 ввести В$3:Е$3.
• В массив 2 ввести В4:Е4.
• Готово. На экране: в F4 введена функция, как показано на рис. 3.
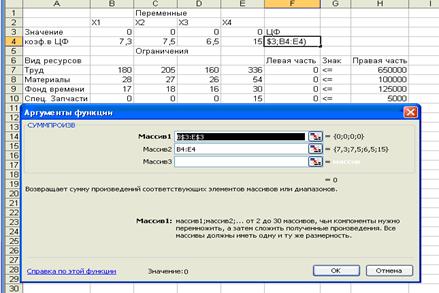
Рис. 3
5.Введем зависимость для левых частей ограничений:
• Курсор в F4.
• Копировать в буфер.
• Курсор в F7.
• Вставить из буфера.
• Курсор в F8.
• Вставить из буфера.
• Курсор в F9.
• Вставить из буфера.
На этом ввод зависимостей закончен.
Запуск Поиска решения
После выбора команд Сервис =>Поиск решения появится диалоговое окно Поиск решения (рис. 4).
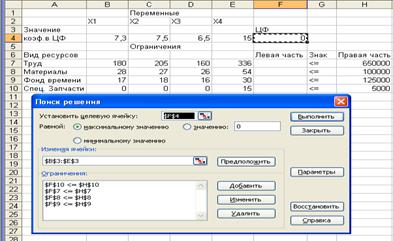
Рис. 4
В диалоговом окне Поиск решения есть три основных параметра:
• Установить целевую ячейку.
• Изменяя ячейки.
• Ограничения.
Сначала нужно заполнить поле «Установить целевую ячейку». Во всех задачах для средства Поиск решения оптимизируется результат в одной из ячеек рабочего листа. Целевая ячейка связана с другими ячейками этого рабочего листа с помощью формул. Средство Поиск решения использует формулы, которые дают результат в целевой ячейке, для проверки возможных решений. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или же установить конкретное значение.
Второй важный параметр средства Поиск решения – это параметр.
Изменяемые ячейки – это те ячейки, значения в которых будут изменяться для того, чтобы оптимизировать результат в целевой ячейке. Для поиска решения можно указать до 200 изменяемых ячеек. К изменяемым ячейкам предъявляется два основных требования: они не должны содержать формул, и изменение их значений должно отражаться на изменении результата в целевой ячейке. Другими словами, целевая ячейка зависима от изменяемых ячеек.
Третий параметр, который нужно вводить для Поиска решения – это Ограничения.
6.Назначение целевой функции (установить целевую ячейку).
• Курсор в поле «Установить целевую ячейку».
• Ввести адрес $F$4.
• Ввести направление целевой функции: Максимальному значению.
• Ввести адреса искомых переменных:
• Курсор в поле «Изменяя ячейки».
• Ввести адреса В$3:Е$3.
7. Ввод ограничений.
• Курсор в поле «Добавить». Появится диалоговое окно Добавление ограничения (рис. 5).
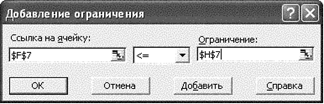
Рис. 5
• В поле «Ссылка на ячейку» ввести адрес $F$7.
• Ввести знак ограничения ≤.
• Курсор в правое окно.
• Ввести адрес $Н$7.
• Добавить. На экране опять диалоговое окно Добавление ограничения.
• Ввести остальные ограничения.
• После ввода последнего ограничения ввести ОК.
На экране появится диалоговое окно Поиск решения с введенными условиями (рис. 5).
8.Ввод параметров для решения ЗЛП (рис. 6).
• Открыть окно Параметры поиска решения.
• Установить флажок Линейная модель, что обеспечивает применение симплекс-метода.
• Установить флажок Неотрицательные значения.
• ОК.
В открывшемся окне «Поиск решения» ввести «Выполнить».
Полученное решение (рис. 7) означает, что максимальную прибыль 26537,7 тыс. руб. депо может получить при выпуске из ремонта 2595,5 полувагонов, 345,4 крытых вагонов, 333,3 вагонов-хопперов. Приэтом ремонт платформ в оптимальном плане производства отсутствует. Ресурсы – рабочее время, материалы, специальные запасные части – будут использованы полностью, а из 125 тыс. ч фонда времени вагоноремонтных позиций будет использовано только 60,3 тыс. ч.
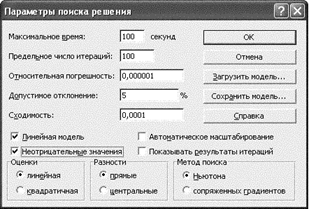
Рис. 6
EXCEL позволяет представить результаты поиска решения в форме отчета. Существует три типа таких отчетов:
Результаты (Answer). В отчет включаются исходные и конечные значения целевой и влияющих ячеек, дополнительные сведения об ограничениях.
Устойчивость (Sensitivity). Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы (Limits). Помимо исходных и конечных значений изменяемых и целевой ячеек в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
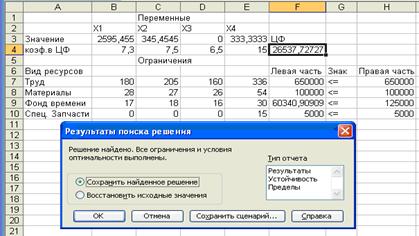
Рис. 7
В отчете по результатам содержатся оптимальные значения переменных X1, Х2, Хз, Х4, значение целевой функции, а также левые части ограничений.
| Microsoft Excel 10.0 Отчет по результатам |
| ||||||
| Рабочий лист: (Методичк.ОПТ.ВАГ.xls)Лист1 |
| ||||||
| Отчет создан: 26.07.2005 4:23:00 |
| ||||||
| |||||||
| |||||||
| Целевая ячейка (Максимум) |
| ||||||
| Ячейка | Имя | Исходное значение | Результат | ||||
| $F$4 | коэф.в ЦФ ЦФ | 26537,72727 | 26537,72727 | ||||
| Изменяемые ячейки | |||||||
| Ячейка | Имя | Исходное значение | Результат | ||||
| $B$3 | Значение Х1 | 2595,454545 | 2595,454545 | ||||
| $C$3 | Значение Х2 | 345,4545455 | 345,4545455 | ||||
| $D$3 | Значение Х3 | 0 | 0 | ||||
| $E$3 | Значение Х4 | 333,3333333 | 333,3333333 | ||||
| Ограничения | |||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | ||
| $F$8 | Материалы Левая часть | 100000 | $F$8<=$H$8 | связанное | 0 | ||
| $F$7 | Труд Левая часть | 650000 | $F$7<=$H$7 | связанное | 0 | ||
| $F$9 | Подобное:
Copyright © https://www.referat-web.com/. All Rights Reserved | ||||||
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

