Математические методы экономических исследований
Международный институт
экономики и права
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЙ
Контрольная работа
Тема 1. Системы, системный подход, системный анализ. Основные термины, определения, технологии
1. Понятие системы.
2. Системный подход, принципы системного подхода.
3. Системный анализ: постановка задачи, декомпозиция, композиция системы, исследование системы.
4. Структура системы.
Краткое содержание темы
Вообще строго определенного понятия системы в настоящее время не существует. Однако, для целей экономического исследования наиболее приемлемым будет следующее определение:
Система - это целостная совокупность элементов любого типа, взаимосвязанных между собой, взаимодействие которых обеспечивает достижение поставленной цели.
Таким образом, для системы характерно наличие:
· совокупности элементов;
· взаимосвязи элементов через структуру;
· взаимодействия;
· целенаправленности.
Элемент системы - это структурная единица системы, не подлежащая делению в данных условиях рассмотрения системы.
Основным свойством системы является то, что она обладает характеристиками, принципиально отличными от характеристик составляющих ее элементов. Только интегративное взаимодействие ее элементов позволяет системе достигнуть уникальных свойств.
Системный подход - это конкретно-научный метод диалектической методологии, имеющей общенаучное значение. Методология изучения системы как единого целого, состоящего из отдельных частей, с различных точек зрения формализации позволяет сформулировать следующие принципы системного подхода.
Принцип конечной цели: абсолютный приоритет конечной (глобальной ) цели.
Принцип единства: совместное рассмотрение системы как целого и как совокупности частей (элементов).
Принцип связности: рассмотрение любой части совместно с ее связями с окружением.
Принцип модульного построения: выделение модулей (подсистем) в системе и рассмотрение ее как совокупность подсистем.
Принцип иерархии: выделение иерархии частей (элементов) и (или) их ранжирование.
Принцип функциональности: совместное рассмотрение структуры и функций с приоритетом функций над структурой.
Принцип развития: учет изменяемости системы, ее способности к развитию, расширению, замене частей, накапливанию информации.
Принцип децентрализации: сочетание в принимаемых решениях управления централизации и децентрализации.
Принцип неопределенности: учет неопределенностей и случайностей в системе.
Совокупность приемов и методов для изучения сложных систем представляет собой системный анализ. Системный анализ - это средство и технология системного подхода.
Рассмотрим основные этапы системного анализа.
1. Постановка задачи. Она включает:
· определение объекта исследования;
· постановку целей;
· задание критериев для изучения объекта и управления им.
Этап слабоформализуем. Успех постановки задачи определяется в основном искусством и опытом системного аналитика, глубиной понимания им поставленной проблемы.
2. Структуризация и очертание границ (декомпозиция) изучаемой системы. Она включает:
· разбиение совокупности всех объектов и процессов, отвечающих поставленной цели, на два класса: собственно исследуемую систему и внешнюю среду;
· изучение процессов взаимодействия объектов (элементов) системы и внешней среды.
Этап слабоформализуем. Он основан на искусстве и опыте проводящих этот этап специалистов.
Разбиение объектов и процессов осуществляется в результате последовательного перебора и включения в систему объектов и процессов, оказывающих заметное влияние на процесс достижения поставленной цели.
3. Составление модели изучаемой системы (как правило, математической).
Параметризация - первый этап этого процесса. Осуществляется описание элементов системы и элементарных воздействий с помощью тех или иных параметров. Параметры могут принимать как непрерывные, так и дискретные числовые значения, а также значения в виде признаков, которые не могут быть охарактеризованы с помощью обычных числовых параметров, а различаются качественно (например: теплый, холодный, плохой, хороший).
Установление различного рода зависимостей между введенными параметрами. Характер этих зависимостей может быть любым. Количественные (числовые) параметры связываются зависимостями типа систем уравнений (обыкновенных алгебраических или дифференциальных). Качественные параметры связываются зависимостями типа таблиц. В общем случае могут встречаться комбинации зависимостей различных типов.
Зависимости между параметрами в системах задаются в общем случае не простыми формулами, а произвольными алгоритмами с использованием любых средств как количественных, так и описательных.
Выделение подсистем и установление их иерархии преследует цель не только упрощения описания системы. Этот процесс дает возможность осуществлять уточнение первоначальной структуризации (разбиения на элементы) и параметризации системы.
Результатом этого этапа является законченная математическая модель системы, описанная на формальном языке.
4. Исследование полученной (построенной) системы - четвертый этап системного анализа.
Первая задача этапа - прогноз развития изучаемой системы.
Для решения этой задачи задают различные предположения о внешних воздействиях на систему в течение рассматриваемого периода и с помощью модели определяют распределение значений, характеризующих систему параметров для любых фиксированных моментов времени.
Термин “прогноз развития” подчеркивает то обстоятельство, что для системы нельзя определить единственную траекторию развития, можно определить лишь множество таких траекторий. При этом каждая траектория может реализоваться в действительности лишь с той или иной степенью вероятности.
Получив прогноз развития изучаемой системы, производят анализ его результатов на соответствие заданным целям и критериям и вырабатывают предложения по улучшению управления и т.д., пока не получится удовлетворяющий результат.
Под структурой системы понимается организация системы из отдельных элементов с их взаимосвязями, которые определяются распределением функций и целей, выполняемых системой.
Структура - это способ организации целого из составных частей .
Эффективность структуры определяется качеством, значением, формой и содержанием ее составных частей, а также местом, которое занимают они в целом, и существующими между ними отношениями.
По принципам управления и подчиненности различают структуры (системы): централизованные, децентрализованные, смешанные.
Централизованная система: задания отдельным элементам системы выдаются лишь одним элементом более высокого уровня.
Децентрализованная система: решения отдельными элементами системы принимаются независимо и не корректируются системой более высокого уровня.
В смешанной системе некоторые функции или этапы выполняются по централизованной системе, а другие - по децентрализованной.
По числу уровней иерархии различают системы: одноуровневые, многоуровневые.
Многоуровневые могут быть однородными и неоднородными.
По выполняемым функциям и целевому назначению различают системы: физические, экономические, биологические, общественные, информационные и т.д.
В зависимости от числа элементов системы и связей между ними различают системы фиксированной (жесткой) и изменяемой (управляемой или переменной) структуры.
По принципам разбиения систем на подсистемы различают структуры систем, в которых элементы объединяются по функциональному и (или) объектному принципам. При объектном разбиении различают структуры отраслевых систем, региональных систем, территориальных систем.
Тема 2. Экономико-математические методы. Состав, структура, направленность, классификация
1. Методы математической статистики.
2. Методы исследования операций и оптимизации.
3. Кибернетические методы.
4. Методы экспертных оценок.
Краткое содержание темы
Основой моделирования экономических систем и протекающих в них процессов являются экономико-математические методы. Рассмотрим состав и структуру экономико-математических методов, применяемых в современной экономической науке и практике.
К старейшим и наиболее используемым классам экономико-математических методов относятся методы математической статистики. Эти методы используются для анализа деятельности экономических систем и включают в себя следующие направления:
· расчет и интерпретация статистических характеристик экономических процессов;
· регрессионный и корреляционный анализ;
· планирование эксперимента.
Следующим классом экономико-математических методов являются методы исследования операций и оптимизации. Это наиболее разработанная группа экономико-математических методов, позволяющих осуществить формализованный анализ экономических систем и процессов.
Среди методов исследования операций и оптимизации различают следующие направления:
· методы математического программирования;
· теорию массового обслуживания и расписаний;
· сетевые методы планирования и управления;
· теорию игр;
· методы эвристики.
Основными направлениями методов кибернетики в экономике являются следующие:
· методы распознавания образов;
· методы классификации;
· методы АСУ;
· методы теории автоматического регулирования;
· имитационное моделирование.
Наконец, одним из направлений экономико-математических методов являются методы экспертных оценок. Эти методы используются для исследования сложных слабоформализуемых систем. Появление мощных программно-математических средств типа экспертных оболочек позволяет надеяться, что в недалеком будущем метод экспертных оценок станет преобладающим, вобрав в себя все лучшие качества других экономико-математических методов, так как основная цель практически всех экономических исследований сводится к оценке текущего состояния исследуемого объекта (процесса) и выдаче прогнозов по его дальнейшему развитию.
Тема 3. Межотраслевой баланс. Состав, структура, схема
1. Состав, структура и схема межотраслевого баланса.
2. Задача и матрица Леонтьева.
Краткое содержание темы
Идея сбалансированности является основой всякого рационального хозяйствования.
Рассмотрим схему народного хозяйства, состоящую из n отраслей, каждая из которых выпускает свой продукт.
В народнохозяйственном механизме все отрасли связаны между собой. Поэтому часть продукции, произведенной i-ой отраслью, потребляется (затрачивается) при функционировании j-ой отраслью. Пусть xij - величина продукции i-ой отрасли, затрачиваемой (используемой) j-ой отраслью. Кроме того, потребителями продукции i-ой отрасли является население и непроизводственные сферы (коммунальные хозяйства, культурно-просветительные учреждения, сфера услуг и т.п.).
Пусть далее, vj - объем конечного продукта j-ой отрасли. Очевидно, он включает dj - непроизводственное потребление (включая вложения в непроизводственные фонды) и bj - накопления производственных фондов.
Пусть далее, wj - общий объем производства j-ой отрасли, тогда имеем следующие соотношения:
![]() , j = 1, 2, ..., n, (3.1)
, j = 1, 2, ..., n, (3.1)
где 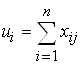 – общее промышленное и производственное потребление, далее:
– общее промышленное и производственное потребление, далее:
![]() ,
,
где vj - непроизводственное потребление и накопление.
В принципе формула (3.1) представляет математическую модель межотраслевого баланса в сфере потребления.
Отрасль можно анализировать не только с точки зрения распределения ее продукции, но и с точки зрения затрат на производство в данной отрасли. Пусть в этом случае в i-ой отрасли имеются затраты на заработную плату zi , кроме этого в балансе необходимо предусмотреть доход Di (i = 1, 2, ..., n). Тогда баланс по затратам будет иметь для i-ой отрасли следующий вид:
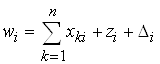 , i = 1, 2, ..., n,
, i = 1, 2, ..., n,
т.е. стоимость продукции i-ой отрасли равна стоимости продукции, затраченной от всех n отраслей, плюс заработная плата и доход от реализации продукции этой отрасли.
Введем определение коэффициента прямых затрат в виде соотношения:
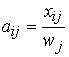 , или
, или ![]() .
.
Подставляя последнее соотношение в (3.1), получим:
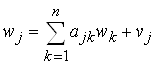 ,
,
или в векторной форме:
w = Aw + v. (3.2)
Пусть себестоимость производства одной единицы продукции j-ой отрасли будет равна cj . Тогда общие народнохозяйственные расходы выражаются соотношением:
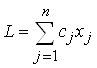 .
.
Ставится следующая задача оптимизации плана ![]() , когда:
, когда:
![]() ,
,
а линейная форма L обращается в минимум.
Таким образом, приходим к так называемой статической модели межотраслевого баланса.
Очевидно, что условиям задачи может удовлетворять множество наборов значений xi (i = 1, 2, ..., n). Каждый такой набор носит название допустимого решения (стратегии, управления, плана). То решение, которое доставляет минимум целевой функции (линейной форме L) называется оптимальным.
Поиск решения задачи межотраслевого баланса путем обращения матрицы (I - A) в различных аспектах был предложен Леонтьевым В., и в научных кругах задача с матрицей (I - A) называется задачей Леонтьева.
Матрица A получила название матрицы Леонтьева. Матрица (I-A)-1 называется матрицей коэффициентов полных затрат. Основной результат межотраслевого анализа может быть сформулирован в виде матричного равенства:
w = (I - A)-1 v . (3.3)
Матрица A называется продуктивной, если матрица ![]() (положительная). Нормой матрицы A назовем максимум сумм элементов ее столбцов. Она обозначается ||A||. Можно доказать, что если A положительная матрица и
(положительная). Нормой матрицы A назовем максимум сумм элементов ее столбцов. Она обозначается ||A||. Можно доказать, что если A положительная матрица и ![]() , причем хотя бы для одного столбца сумма его элементов строго меньше 1, то A будет продуктивной матрицей.
, причем хотя бы для одного столбца сумма его элементов строго меньше 1, то A будет продуктивной матрицей.
Тема 4. Задачи на смеси
1. Постановка задачи на смеси.
2. Графический метод решения.
3. Общий алгоритм решения задач линейного программирования.
Краткое содержание темы
Задачи на смеси являются одним из показательных классов задач по линейному программированию в области планово-экономических исследований. На примере таких задач могут быть рассмотрены основные методы решения задач линейного программирования как одного из крупных разделов математических методов экономических исследований.
Классическая задача на смеси ставится следующим образом. Из различных видов сырья объемом соответственно b1, b2,..., bm-1, bm можно изготовить n видов продукции. Пусть цена единицы j-го вида продукции будет cj и для изготовления единицы j-го продукта требуется затратить i-ый вид сырья в количестве aij единиц. Возникает вопрос, какие виды продукции и в каком количестве нужно производить, чтобы получить наибольшую выручку?
Таким образом, нужно определить количество производимой продукции при ограниченных ресурсах, при этом реализация произведенной продукции должна дать максимальную выручку.
Математически описанную задачу можно представить следующим образом.
Пусть ![]() - количество j-ой продукции, тогда стоимость всей произведенной продукции можно выразить функцией:
- количество j-ой продукции, тогда стоимость всей произведенной продукции можно выразить функцией:
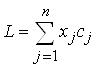 ‑ целевая функция.
‑ целевая функция.
Следовательно, в задаче идет речь о достижении максимума целевой функции L на множестве различных допустимых значений ![]() . Другими словами, критерием оптимальности задачи является:
. Другими словами, критерием оптимальности задачи является: ![]() .
.
Очевидно, далее, что ![]() ³ 0 для j = 1, 2,..., n. Количество произведенной продукции не может быть отрицательным. Далее, на единицу j-го вида продукции требуется
³ 0 для j = 1, 2,..., n. Количество произведенной продукции не может быть отрицательным. Далее, на единицу j-го вида продукции требуется ![]() единиц i-го сырья, т.е. для изготовления
единиц i-го сырья, т.е. для изготовления ![]() единиц j-го продукта потребуется
единиц j-го продукта потребуется ![]() единиц i-го сырья.
единиц i-го сырья.
Так как один и тот же вид сырья может использоваться для производства любого j-го продукта, то суммарные потребности i-го сырья на все j-ые продукты не должны превышать имеющихся ресурсов b1, b2, ..., bm сырья, т.е.
 .
.
Таким образом, приходим к следующей математической задаче.
Найти: 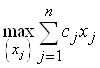 при условии, что
при условии, что ![]() и
и 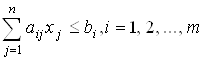 .
.
Очевидно, что условиям задачи может удовлетворить множество наборов значений xj, где j = 1, 2, ..., n. Каждый из таких наборов носит название допустимого решения (стратегии, управления, плана). Решение, при котором достигается max целевой функции, называется оптимальным.
Графический метод решения задачи на смеси вытекает из следующих основных свойств задач линейного программирования:
· существует выпуклый многоугольник (многогранник) допустимых решений;
· оптимальное решение задачи достигается в одной из вершин многоугольника допустимых решений.
Следовательно, если построить гиперплоскость целевой функции (критерия) нулевого уровня, то, передвигая ее в сторону возрастания значений переменных, можно определить первую или последнюю вершину многоугольника допустимых решений для поставленной задачи, с которой передвигаемая гиперплоскость впервые встречается или покидает область многоугольника. В частном случае гиперплоскость может представлять прямую линию. Соответственно первая вершина встречи будет определять минимальное значение целевой функции, а последняя вершина встречи - максимальное.
Общий алгоритм решения задач линейного программирования
Без ограничения общности имеем следующую задачу линейного программирования:
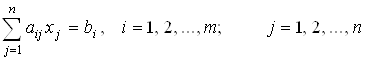 , (4.1)
, (4.1)
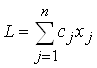 .
.
Найти среди допустимых ![]() , j = 1, 2, ..., n, такие, что:
, j = 1, 2, ..., n, такие, что:
![]() .
.
Основные шаги решения сформулированной задачи следующие.
1. Находится хотя бы одно из неотрицательных решений ![]() .
.
2. Подставляем в систему полученное решение, в результате чего получаем новую систему, эквивалентную исходной:
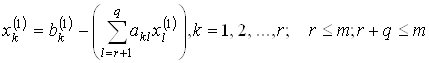 .
.
3. Подставляем выражения основных переменных в L:
 .
.
4. Применяем последовательность тождественных преобразований к полученной системе и линейной форме до тех пор, пока не исчезнут положительные коэффициенты при переменных в линейной форме, т.е. нарушатся условия ее существования.
После конечного числа указанных шагов (если нет зацикливания) находится оптимальное решение поставленной задачи. В этом заключается суть симплекс-метода.
Возникает вопрос. Как найти хотя бы одно неотрицательное решение системы (4.1)?
Сводим исходную систему (4.1) к виду:
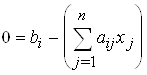 , i = 1, 2, ..., m. (4.2)
, i = 1, 2, ..., m. (4.2)
Если в этой системе имеется переменная, входящая только в одно уравнение, и коэффициент при ней имеет знак «+», то уравнение можно разрешить относительно этой переменной.
Считаем, что в (4.2) уравнения разрешены относительно всех таких переменных, тогда, сделав перенумерацию, имеем:
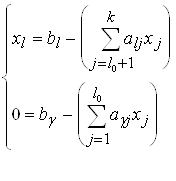 (4.3)
(4.3)
l = 1, 2, ..., l0; = 1, 2, ..., 0;
l0 + 0 = m; l0 + k = n; ![]() .
.
Любое уравнение в (4.3), неразрешенное относительно какой-либо переменной, будем называть 0-уравнением.
Для системы (4.3) неотрицательное решение отыскивается последовательными тождественными преобразованиями, удовлетворяющими следующим условиям:
1. Отыскиваем 0-уравнение, у которого свободный член ![]() (если такого свободного члена нет, то значения переменных xl = bl,
(если такого свободного члена нет, то значения переменных xl = bl, ![]() , l = 1, 2, ..., l0; j = 1, 2, ..., k образуют неотрицательное решение системы (4.3)). Пусть это будет i-ое уравнение.
, l = 1, 2, ..., l0; j = 1, 2, ..., k образуют неотрицательное решение системы (4.3)). Пусть это будет i-ое уравнение.
2. Отмечаем в i-ом уравнении положительный коэффициент ![]() .
.
3. Находим разрешающий элемент ![]() и производим торжественное преобразование (4.3).
и производим торжественное преобразование (4.3).
4. i-ое 0-уравнение используется до тех пор, пока либо разрешим его, либо придем к несовместимости системы (4.3).
5. После разрешения i-го уравнения отыскиваем следующее 0-уравнение с положительным свободным членом и производим с ним аналогичные действия.
6. Процесс продолжается до тех пор, пока не освободимся от всех 0-уравнений.
В результате можем получить:
а) после конечного числа тождественных преобразований система освободится от 0-уравнений. Тогда система будет совместимой. Совокупность значений переменных, получаемых приравниванием неосновных переменных нулю, а основных - свободным членам в системе, не содержащей 0-уравнений, является неотрицательным решением исходной системы;
б) После конечного числа тождественных преобразований обнаружится, что используемое 0-уравнение превращается в уравнение вида:
![]() ,
,
где ![]() , т.е. для всех j - система несовместна;
, т.е. для всех j - система несовместна;
в) система не освобождается полностью от 0-уравнений, а условия тождественных преобразований не нарушаются. Число 0-уравнений не увеличивается, а некоторые из них имеют по крайней мере один положительный коэффициент в правой части, но разрешающий элемент ему не принадлежит.
Тема 5. Транспортная задача
1. Постановка транспортной задачи.
2. Общий подход к решению транспортной задачи.
Краткое содержание темы
Среди задач линейного программирования выделяется класс задач, условия постановки которых в определенной степени позволяют упростить процедуру их решения и определить специфические алгоритмы нахождения этих решений. Этот класс задач получил название "Транспортные задачи".
Рассмотрим постановку таких задач.
Пусть имеем m предприятий A1, A2,..., Am, производящих один и тот же продукт в количествах соответственно a1, a2,..., am.
Пусть, далее, имеется n потребителей (складов) B1, B2,..., Bn с потребностями (вместимостями) соответственно b1, b2,..., bn.
Пусть весь произведенный продукт может быть размещен на складах B1, B2,..., Bn при полном их заполнении.
Пусть, наконец, перевозка единицы продукции из пункта Ai в пункт Bj оценивается величиной cij (cij - заданы).
Необходимо определить наилучший план перевозок по стоимости, т.е. такой план, который давал бы минимальную стоимость перевозок всей произведенной продукции на склады.
Строим математическую модель. Пусть xij - количество продукта, перевозимого из пункта Ai в пункт Bj. Из постановки задачи очевидно, что каждый склад вмещает:
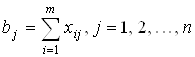 .
.
А так как производится столько продукции, сколько ее потребляется (складируется), то:
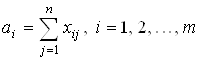
(продукт с предприятия вывозится полностью).
Далее, очевидным является то, что количество перевозимой с предприятия на склад продукции не может быть отрицательным, т.е. ![]() (i = 1, 2, ..., m; j = 1, 2, ..., n).
(i = 1, 2, ..., m; j = 1, 2, ..., n).
Так как необходимо определить наилучший план перевозок по стоимости, то строим целевую функцию суммарных затрат на перевозки. Она должна быть минимизирована. Такая целевая функция имеет вид:
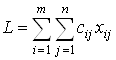 .
.
Таким образом, имеем следующую математическую постановку задачи. Найти такие xij, которые доставляют минимум линейной форме L, т.е. 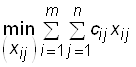 и удовлетворяют условиям:
и удовлетворяют условиям:
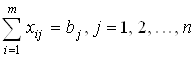 (1)
(1)
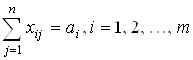 (2)
(2)
![]() (3)
(3)
(Из (1) и (2) следует, что 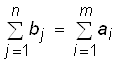 . Именно в этом соотношении заключается основная специфика выделенного класса задач, так как это соотношение определяет дополнительное условие (как бы скрытое), которое позволяет произвольным образом распорядиться одной из переменных xij, а тем самым упростить решение задачи).
. Именно в этом соотношении заключается основная специфика выделенного класса задач, так как это соотношение определяет дополнительное условие (как бы скрытое), которое позволяет произвольным образом распорядиться одной из переменных xij, а тем самым упростить решение задачи).
Рассмотрим теперь подходы к решению транспортной задачи в общем виде, т.е. задачи размерности m x n.
Введем следующие понятия:
· прямоугольная цепь;
· независимые расположения;
· подходящие решения.
Понятие прямоугольной цепи исходит из следующих соображений. Пусть имеется некоторое допустимое решение задачи, которое может быть не оптимизирует решение. Тогда это решение необходимо изменить. Но изменение хотя бы одной компоненты решения (количества продукции, перевозимой хотя бы по одному из путей) приводит к изменению общей суммы перевозок в соответствующей строке и столбце таблицы решений. Следовательно, в свою очередь необходимо изменить другие компоненты решения так, чтобы были "восстановлены" первоначальные значения указанных сумм. Схематически такое "восстановление" может быть наглядно изображено в виде прямоугольной диаграммы или, иначе, цепи, которая связывает четыре клетки в таблице перевозок. Например:
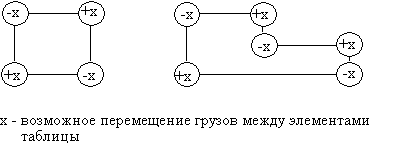
Очевидно, что любое множество допустимых изменений плана перевозок (т.е. изменений, которые сохраняют значения сумм по столбцам и строкам) должно быть эквивалентно серии прямоугольных цепей.
Будем говорить, что клетки матрицы перевозок, определяющей допустимое решение, расположены независимо, если прямоугольная цепь, содержащая эти клетки матрицы, имеет хотя бы одну нулевую клетку.
Подходящие решения - это последовательность допустимых решений, удовлетворяющих условиям:
· матрица перевозок каждого решения содержит ровно (m+n-1) ненулевых клеток;
· клетки матрицы перевозок независимо расположены.
Можно указать способ нахождения последовательности подходящих решений, для которых транспортные издержки будут постоянно уменьшаться до тех пор, пока не будет достигнуто оптимальное решение с минимальными затратами.
Существуют разные методы, упрощающие процедуру исследования всех допустимых изменений размещения грузов и позволяющие быстро находить нужные решения. Одним из таких методов является метод теневых затрат.
Тема 6. Метод динамического программирования (ДП)
1. Понятие метода ДП.
2. Принцип решения задачи ДП.
3. Задача распределения ресурсов.
4. Практические рекомендации по постановке задач ДП.
Краткое содержание темы
Общее понятие метода ДП
Динамическое программирование (или "динамическое планирование") - это метод оптимизации так называемых многошаговых (многоэтапных) операций (задач). Пусть имеем задачу G, распадающуюся на ряд последовательных шагов или этапов, например, деятельность отрасли промышленности в течение ряда хозяйственных лет (m -лет). Пусть эффективность решения задачи (операции) описывается показателем W (назовем его "выигрыш") и пусть он складывается из выигрышей на отдельных шагах, т.е.: 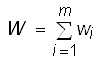 - аддитивный критерий.
- аддитивный критерий.
Пусть операция (задача) является управляемой, т.е. выбираются какие-то параметры, которые влияют на ход и исход. На каждом шаге выбирается какое-то решение, от которого зависит выигрыш на данном шаге и выигрыш на операции в целом, - шаговое управление. Совокупность всех шаговых управлений есть управление операцией (задачей) в целом. Обозначив его Х, а шаговое управление х1, x2, ..., хm, имеем:
![]() , хi - может принимать любые значения (числа, векторы, функции и т.д.).
, хi - может принимать любые значения (числа, векторы, функции и т.д.).
Требуется найти такое управление Х, при котором выигрыш W обращается в максимум: 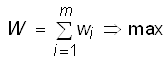 .
.
x = x *, при котором это случается, называется оптимальным управлением: ![]() .
.
Пусть ![]() , максимум берется по всем управлениям х, (возможным в данных условиях), т.е. возможна запись:
, максимум берется по всем управлениям х, (возможным в данных условиях), т.е. возможна запись: ![]() .
.
Принцип решения задачи ДП.
Метод ДП не предполагает, что каждый шаг оптимизируется отдельно, независимо от других.
Пусть, например, планируется работа группы предприятий, часть из которых выпускает предметы потребления, а остальные производят для них машины. Задача - за m лет получить максимальный объем предметов потребления.
Пусть планируются инвестиции на первый год. Если исходить из узких интересов этого шага (года), то можно было бы вложить все наличные средства в производство предметов потребления. Но такое решение не было бы правильным (эффективным) с точки зрения операции в целом. Конечно, вкладывая средства в производство машин, мы сокращаем объем производства предметов потребления в данном году, но, однако, вместе с этим создаются условия для увеличения производства в последующие годы.
Итак, планируя многошаговую задачу, необходимо выбирать управление на каждом шагу с учетом всех его будущих последствий на еще предстоящих шагах.
Управление на i-том шаге выбирается так, чтобы была максимальной сумма выигрышей на всех оставшихся до конца шагах плюс данный.
Однако, последний шаг является исключением из этого правила. Здесь можно планировать так, чтобы он сам, как таковой, принес наибольшую выгоду.
Следовательно, процесс ДП обычно разворачивается от конца к началу, т.е. сначала планируется m-й шаг. Но как его спланировать, если не знаем, чем кончается предпоследний шаг. Как быть?
Планируя последний шаг, нужно сделать разные предположения о том, чем кончится предпоследний (m-1)-й шаг, и для каждого из этих предположений найти условное оптимальное управление на m-ом шаге (условное, так как оно выбирается, исходя из условия, что предпоследний шаг кончился так-то и так-то (каким-то образом)).
Предположим, что это сделано, и для каждого из возможных исходов предпоследнего шага известно условное оптимальное управление и соответствующий ему условный оптимальный выигрыш на m - ом шаге.
Теперь можно оптимизировать управление на предпоследнем (m-1)-ом шаге. Снова делаем возможные предположения о том, чем может кончиться предыдущий (m-2)-й шаг и для каждого из этих предположений находим такое управление на (m-1)-ом шаге, при котором выигрыш за последние два шага ( m-й уже оптимизирован) максимален. Так находятся для каждого исхода (m-2)-го шага условное оптимальное управление на (m-1)-м шаге и условный оптимальный выигрыш на двух последних шагах. И так, "пятясь назад", оптимизируем управление на (m-2)-м шаге и т.д., пока не дойдем до первого. Предположим, что все условные оптимальные управления и выигрыши за весь" хвост" процесса (на всех шагах, начиная от данного и до конца) известны. Теперь можно найти не условные оптимальные управления x* и w*.
Действительно, пусть известно, что в каком-то состоянии S0 управляемая система (объект управления S) была в начале первого шага. Тогда можно выбрать оптимальное управление х1* на первом шаге. Применив его, меняем состояние системы на некоторое новое S1*. В этом состоянии подходим ко второму шагу. Тогда тоже известно условное оптимальное управление x2*, которое к концу второго шага переводит систему в состояние S2* и т.д. Оптимальный выигрыш w* за всю операцию известен, так как именно на основе его максимальности выбиралось управление на первом шаге.
Таким образом, в процессе оптимизации управления методом ДП многошаговый процесс "проходится" дважды:
· от конца к началу - поиск условных оптимальных управлений и выигрышей за оставшийся "хвост" процесса;
· от начала к концу - осуществляется "чтение" уже готовых рекомендаций и поиск безусловного оптимального управления x*, состоящего из оптимальных шаговых управлений x1*, x2*, ..., xm*.
Задача о распределении ресурсов
Имеется некий запас ресурсов (средств) К, который нужно распределить между предприятиями А1, А2, ..., Аm. Каждое i-ое предприятие при вложении в него каких-то средств x приносит доход в виде функции ![]() . Все
. Все ![]() заданы (пусть они неубывающие). Как распределить средства К между Ai (i =1,2,...,m), чтобы в сумме они дали максимальный доход?
заданы (пусть они неубывающие). Как распределить средства К между Ai (i =1,2,...,m), чтобы в сумме они дали максимальный доход?
Здесь нет параметра времени. Однако, операцию распределения средств можно мысленно развернуть в какой-то последовательности, считая за первый шаг вложение в предприятие А1, за второй - вложение в предприятие А2 и т.д.
Управляемая система S в данном случае - это ресурсы (средства). Состояние системы S перед каждым шагом характеризуется одним числом S -наличным запасом еще не вложенных средств.
Шаговыми управлениями являются средства х1, x2, ..., хm, выделяемые конкретным предприятиям.
Требуется найти оптимальное управление, т.е. совокупность х1, x2, ..., хm, при которой суммарный доход максимален:
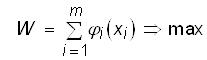 .
.
Решение в общем виде
Находим для каждого i-го шага условный оптимальный выигрыш (от этого шага и далее до конца), если к данному шагу подошли с запасом средств S. Обозначаем условный оптимальный выигрыш wi(S), а соответствующее ему условное оптимальное управление - средства, вкладываемые в i-е предприятие, - xi(S).
Начинаем оптимизацию с последнего m-го шага.
Пусть подошли к этому шагу с остатком средств S. Вкладываем всю сумму S целиком в предприятие Аm. Следовательно, условное оптимальное управление на m-ом шаге: отдать последнему предприятию все имеющиеся средства S:
![]() ,
,
а условный оптимальный выигрыш:
![]() .
.
Задаваясь последовательностью значений S (располагая их достаточно тесно), для каждого значения S будем знать xm(S) и wm(S). Последний шаг оптимизирован.
Переходим к предпоследнему (m-1)-му шагу. Пусть подошли к нему с запасом средств S. Обозначим wm-1(S) условный оптимальный выигрыш на двух последних шагах: (m-1)-ом и m-ом (последний оптимизирован). Если на (m-1)-ом шаге (m-1)-му предприятию выделим средств x, то на последний останется S-x. Выигрыш на двух последних шагах будет:
![]()
и нужно найти такое x, при котором этот выигрыш максимален:
![]()
Знак max означает, что берется максимальное значение по всем x, какие только возможны при x £ S (вложить больше, чем S нельзя) от выражения в { }. Этот максимум и есть условный оптимальный выигрыш за два последних шага, а то значение x, при котором max достигается, - условное оптимальное управление на (m-1)-ом шаге.
Далее оптимизируем (m-2)-й, (m-3)-й и т.д. шаги. Для любого i-го шага условный оптимальный выигрыш за все шаги с этого и до конца находятся по формуле:
![]()
и соответствующее ему условное оптимальное управление xi(S) - то значение x, при котором этот максимум достигается.
Продолжая этот процесс, доходим до первого предприятия А1. Варьировать значениями S нет нужды, так как знаем, что запас средств перед первым шагом есть K, т.е.:
![]() .
.
Итак, максимальный выигрыш (доход) от всех предприятий найден. Значение x, при котором достигается max в последнем соотношении и есть оптимальное управление ![]() на первом шаге.
на первом шаге.
После того, как эти средства вложены в первое предприятие, остается ![]() . Читая рекомендацию для этого значения S, выделяем второму предприятию оптимальное количество средств:
. Читая рекомендацию для этого значения S, выделяем второму предприятию оптимальное количество средств:
![]() и т.д. до конца.
и т.д. до конца.
Практические рекомендации по постановке задач ДП
1. Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
2. Расчленить операцию
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Математическое моделирование в управлении
- Анализ и пути совершенствование системы содействия занятости населения (на примере Кемеровского центра занятости)
Современный этап социально-экономического развития страны, характеризующийся одновременным проведением ряда фундаментальных реформ
- Анализ и резервы повышения эффективности использования машинно-тракторного парка СПК ПФ "Горномарийская" Горномарийского района
- Анализ и совершенствование коммерческой деятельности
В условиях рыночной экономики одним из ключевых элементов организации бизнеса является система организации коммерческой деятельности
- Анализ и совершенствование хозяйственной деятельности предприятия (на примере ООО "Эдельвейс")
- Построение эконометрической модели и исследование проблемы автокорреляции с помощью тестов Бреуша-Годфри и Q-статистики
Глава 1. Теоретическое обоснование модели и её анализа 1.1 Экономическое обоснование модели1.2 Проблема автокорреляции: теорияГлава 2. По
- Применение линейного программирования для решения экономических задач (оптимизация прибыли)
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

