Построение эконометрической модели и исследование проблемы автокорреляции с помощью тестов Бреуша-Годфри и Q-статистики
Глава 1. Теоретическое обоснование модели и её анализа
1.1 Экономическое обоснование модели
1.2 Проблема автокорреляции: теория
Глава 2. Построение регрессионной модели и её анализ на проблему автокорреляции
Глава 3. Устранение автокорреляции
Заключение
Список использованных источников
Приложение 1
Приложение 2
Приложение 3
В данной работе будет построена регрессионная модель, которая основана на реальных статистических данных. Среди основных задач выделяются:
- построение качественной модели линейной регрессии и доказательство справедливости соответствующего ей теоретического уравнения экономической теории;
- демонстрация работы тестов Бреуша-Годфри и Q-теста, позволяющих определить наличие автокорреляции в модели;
- при обнаружении последней рассмотрение варианты корректирования модели, для того, чтобы выполнялись все предпосылки МНК.
Статистические данные использованных в работе показателей были взяты из Системы Национальных Счетов Российской Федерации. Это поквартальные данные с первого квартала 1999 года по 2-ой квартал 2008 года включительно.
Целью данной работы является доказательство существования определённой зависимости между экономическими показателями, а также более глубокое изучение проблемы автокорреляции в регрессионной модели.
Глава 1. Теоретическое обоснование модели и её анализа
1.1 Экономическое обоснование модели
Для построения регрессионной модели были выбраны следующие экономические показатели:
- ВВП(GDP) – показатель, измеряющий стоимость конечной продукции, произведённой резидентами данной страны за определённый период времени;
- потребительские расходы (Cons, потребление), которые включают в себя расходы домашних хозяйств на товары как длительного, так и текущего пользования (кроме расходов на покупку жилья), а также на услуги;
- инвестиции + государственные расходы (IG), которые включают производственные капиталовложения и расходы государства, например, такие как строительство школ, дорог или содержание армии;
Эти показатели объединены в уравнении, которое получило название основного макроэкономического тождества для закрытой экономики:
![]() (1)
(1)
В данной работе зависимость (1) будет доказываться на справедливость на основе статистических данных, а также будет использоваться в данной работе для построения модели, в которой возможно наличие автокорреляции.
1.2 Проблема автокорреляции: теорияАвтокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени. Автокорреляция чаще встречается в регрессионном анализе при использовании данных временных рядов. В экономических задачах встречается как положительная автокорреляция (![]() ), так и отрицательная (
), так и отрицательная (![]() ).
).
Основными причинами вызывающими появление автокорреляцию считают ошибки спецификации, инерцию в изменении экономических показателей (вследствие цикличности), эффект паутины (причина – временные лаги), а также сглаживание данных.
Среди последствий автокорреляции обычно выделяют следующие:
· Оценки параметров перестают быть эффективными;
· Оценка дисперсии регрессии является смещённой;
· Дисперсии оценок являются смещёнными, что приводит к увеличению t-статистик. Это может привести к признанию статистически значимыми объясняющие переменные, которые на самом деле таковыми не являются;
· Ухудшаются прогнозные качества модели.
Так как последствия автокорреляции для качества модели велики, то важно выявить наличие автокорреляции, что делается с помощью нескольких тестов. Чаще всего используются такие тесты, как метод рядов, критерий Дарбина-Уотсона, тест Бреуша-Годфри, Q-статистика, h-статистика.
Глава 2. Построение регрессионной модели и её анализ на проблему автокорреляции
Поскольку в данной работе при построении уравнения регрессии будут использоваться временные ряды, так как в них чаще встречается проблема автокорреляции, а не перекрёстные данные, то перед построением модели следует проверить ряды на стационарность.
Как видно из Рис.1 Приложения 1 все ряды исследуемых показателей не имеют постоянного математического ожидания, но имеют восходящий линейный тренд, из чего возможно сделать предварительный вывод о том, что ряды будут стационарными относительного тренда.
Для более глубокого анализа рядов на стационарность используются коррелограммы рядов, а также тесты «единичного корня». В данной работе будет рассмотрен тест Дики-Фуллера.
Очевидно, что все три ряда являются нестационарными, что можно определить по характерному рисунку «убывающей экспоненты» на графике автокорреляционной функции, а также первый выступающий лаг на графике частной автокорреляционной функции. Следовательно, проверку исходных рядов на стационарность следует дополнить тестом Дики-Фуллера. Результаты приведены ниже:
| ADF Test Statistic | -20.99004 | 1% Critical Value* | -4.2412 |
| |||||||
| 5% Critical Value | -3.5426 |
| |||||||||
| 10% Critical Value | -3.2032 |
| |||||||||
| Dependent Variable: D(IG) |
| ||||||||||
| Method: Least Squares |
| ||||||||||
| Included observations: 35 after adjusting endpoints |
| ||||||||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| ||||||
| D(IG(-1)) | -2.200495 | 0.104835 | -20.99004 | 0.0000 |
| ||||||
| @TREND(1999:1) | 9.663892 | 2.439289 | 3.961766 | 0.0004 |
| ||||||
| Durbin-Watson stat | 2.352758 | Prob(F-statistic) | 0.000000 |
| |||||||
| ADF Test Statistic | -5.278444 | 1% Critical Value* | -4.2412 |
| |||||||
| 5% Critical Value | -3.5426 |
| |||||||||
| 10% Critical Value | -3.2032 |
| |||||||||
| Dependent Variable: D(CONS) |
| ||||||||||
| Method: Least Squares |
| ||||||||||
| Included observations: 35 after adjusting endpoints |
| ||||||||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| ||||||
| D(CONS(-1)) | -1.636006 | 0.309941 | -5.278444 | 0.0000 |
| ||||||
| @TREND(1999:1) | 12.54844 | 3.021702 | 4.152773 | 0.0002 |
| ||||||
| Durbin-Watson stat | 2.101394 | Prob(F-statistic) | 0.000000 |
| |||||||
| ADF Test Statistic | -9.618956 | 1% Critical Value* | -4.2412 | ||||||||
| 5% Critical Value | -3.5426 | ||||||||||
| 10% Critical Value | -3.2032 | ||||||||||
| Dependent Variable: D(GDP) | |||||||||||
| Method: Least Squares | |||||||||||
| Included observations: 35 after adjusting endpoints | |||||||||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. | |||||||
| D(GDP(-1)) | -2.088636 | 0.217137 | -9.618956 | 0.0000 | |||||||
| @TREND(1999:1) | 26.31412 | 6.414595 | 4.102226 | 0.0003 | |||||||
| Durbin-Watson stat | 2.486933 | Prob(F-statistic) | 0.000000 | ||||||||
При помощи коррелограммы первых разностей данных всех трёх рядов обнаруживается, что необходимо ввести один лаг для всех рядов во вспомогательное уравнение теста. И после того, как был проведён тест Дики-Фуллера, выяснилось, что ряды интегрированы первого порядка или стационарны в первых разностях со спецификацией тренда и одним лагом.
Однако ряды IG и GDP имеют чётко видную сезонность, что видно на Рисунке 1 Приложения 1, поэтому для них дополнительного проводится тест Филипса-Перрона, данные которого находятся в Приложении 2.
Имеем:
- ряды нестационарны в уровнях, но стационарны в первых разностях;
- по имеющимся данным можно строить модель множественной классической линейной регрессии.
По предварительному анализу, можно сказать, что модель, которая будет построена, возможно, будет обладать проблемой автокорреляции вследствие цикличности показателей, используемых для построения уравнения регрессии. ВВП имеет дело с волнообразностью деловой активности, которая при построении модели может служить причиной автокорреляции.
Строим уравнение регрессии:
| Dependent Variable: GDP | ||||
| Method: Least Squares | ||||
| Date: 12/11/08 Time: 16:34 | ||||
| Sample: 1999:1 2008:2 | ||||
| Included observations: 38 | ||||
| GDP=C(1)+C(2)*Cons+C(3)*IG | ||||
| Coefficient | Std. Error | t-Statistic | Prob. | |
| C(1) | 90.71828 | 36.69767 | 2.472045 | 0.0184 |
| C(2) | 0.875856 | 0.076378 | 11.46745 | 0.0000 |
| C(3) | 1.190895 | 0.030510 | 39.03232 | 0.0000 |
| R-squared | 0.998324 | Mean dependent var | 4283.858 | |
| Adjusted R-squared | 0.998228 | S.D. dependent var | 2609.517 | |
| S.E. of regression | 109.8386 | Akaike info criterion | 12.31156 | |
| Sum squared resid | 422257.9 | Schwarz criterion | 12.44084 | |
| Log likelihood | -230.9196 | Durbin-Watson stat | 0.589082 | |
Уравнение регрессии выглядит следующим образом:
GDP=90.71828168+0.8758556601![]() Cons+1.190895181
Cons+1.190895181![]() IG (2)
IG (2)
После округления оно будет иметь следующий вид:
![]() (3)
(3)
Построенная модель имеет очень высокий коэффициент детерминации, что говорит о высоком качестве этой модели. Высокие значения имеют t-статистики, соответственно все объясняющие переменные данной модели значимы. Верны и коэффициенты при переменных, то есть они имеют верный знак и значение близкое к теоретическому уравнению (1). Высокое значение коэффициента С(1) и его статистическая значимость с экономической точки зрения может говорить о том, что в модель включено недостаточно переменных, что позже будет исправлено. Поэтому, прежде чем делать выводы о качестве и адекватности, следует проверить построенную модель на автокорреляцию и гетероскедастичность.
По статистике Дарбина-Уотсона уравнение имеет автокорреляцию, положительную (d1=1,373, du=1,594), откуда можно сделать вывод о наличии автокорреляции.
На проблему гетероскедастичности исследуем модель при помощи теста Вайта(no cross, cross):
| White Heteroskedasticity Test: | ||||
| F-statistic | 1.926499 | Probability | 0.129239 | |
| Obs*R-squared | 7.193728 | Probability | 0.125998 | |
| |||||
| Test Equation: | ||||
| Dependent Variable: RESID^2 | ||||
| Method: Least Squares | ||||
| Date: 12/11/08 Time: 19:18 | ||||
| Sample: 1999:1 2008:2 | ||||
| Included observations: 38 | ||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. |
| C | -7329.568 | 8035.888 | -0.912104 | 0.3683 |
| IG | -10.79329 | 22.84694 | -0.472417 | 0.6397 |
| IG^2 | 0.000343 | 0.007396 | 0.046398 | 0.9633 |
| CONS | 14.94592 | 10.01542 | 1.492291 | 0.1451 |
| CONS^2 | -0.001335 | 0.001299 | -1.028002 | 0.3114 |
| R-squared | 0.189309 | Mean dependent var | 11112.05 | |
| Adjusted R-squared | 0.091043 | S.D. dependent var | 13500.26 | |
| S.E. of regression | 12871.05 | Akaike info criterion | 21.88543 | |
| Sum squared resid | 5.47E+09 | Schwarz criterion | 22.10090 | |
| Log likelihood | -410.8231 | F-statistic | 1.926499 | |
| Durbin-Watson stat | 1.289207 | Prob(F-statistic) | 0.129239 | |
| White Heteroskedasticity Test: | |||||
| F-statistic | 1.910945 | Probability | 0.120009 | ||
| Obs*R-squared | 8.737384 | Probability | 0.120009 | ||
| Test Equation: | |||||
| Dependent Variable: RESID^2 | |||||
| Method: Least Squares | |||||
| Date: 12/11/08 Time: 19:20 | |||||
| Sample: 1999:1 2008:2 | |||||
| Included observations: 38 | |||||
| Variable | Coefficient | Std. Error | t-Statistic | Prob. | |
| C | -4788.651 | 8190.315 | -0.584672 | 0.5629 | |
| IG | 10.01788 | 27.71085 | 0.361515 | 0.7201 | |
| IG^2 | 0.043812 | 0.034248 | 1.279250 | 0.2100 | |
| IG*CONS | -0.034393 | 0.026471 | -1.299253 | 0.2031 | |
| CONS | 5.948824 | 12.09186 | 0.491969 | 0.6261 | |
| CONS^2 | 0.005437 | 0.005368 | 1.012743 | 0.3188 | |
| R-squared | 0.229931 | Mean dependent var | 11112.05 | ||
| Adjusted R-squared | 0.109608 | S.D. dependent var | 13500.26 | ||
| S.E. of regression | 12738.93 | Akaike info criterion | 21.88665 | ||
| Sum squared resid | 5.19E+09 | Schwarz criterion | 22.14522 | ||
| Log likelihood | -409.8464 | F-statistic | 1.910945 | ||
| Durbin-Watson stat | 1.168906 | Prob(F-statistic) | 0.120009 | ||
Для трактовки этого теста используем «Obs*R-squared», которое сравниваем с соответствующим критическим значением ![]() распределения со степенями свобод равным количеству переменных в модели, то есть двум. Как и в тесте cross terms, так и в no cross terms наблюдаемое значение оказывается меньше критического при уровнях значимости
распределения со степенями свобод равным количеству переменных в модели, то есть двум. Как и в тесте cross terms, так и в no cross terms наблюдаемое значение оказывается меньше критического при уровнях значимости ![]() ,01 и
,01 и ![]() ,005, из чего следует вывод об отсутствии гетероскедастичности в построенной модели.
,005, из чего следует вывод об отсутствии гетероскедастичности в построенной модели.
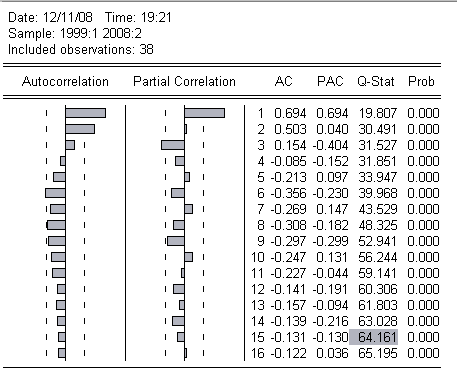
Проблему автокорреляции исследуем далее при помощи теста Бреуша-Годфри и Q-статистики Бокса-Льюнга. Результаты этих тестов представлены ниже:
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

