Скачать

Математическая статистика

ИДА Кривой Рог IBM

Частное Учебное Заведение

Институт Делового Администрирования

Private Educational Institution

Institute of Business Managment

Кафедра информационных систем

и

высшей математики

Математическая cтатистика

Конспект лекций

для специальностей УА, ФК 1995

© Г.И. Корнилов

1997

Введение в курс Основные определения

Несмотря на многообразие используемых в литературе определений термина “статистика”, суть большинства из них сводится к тому, что статистикой чаще всего называют науку, изучающую методы сбора и обработки фактов и данных в области человеческой деятельности и природных явлений.

В нашем курсе, который можно считать введением в курс “Экономическая статистика”, речь будет идти о так называемой прикладной статистике, - т.е. только о сущности специальных методов сбора, обработки и анализа информации и, кроме того, о практических приемах выполнения связанных с этим расчетов.

Великому американскому сатирику О’Генри принадлежит ироническое определение статистики: “Есть три вида лжи - просто ложь, ложь злостная и …статистика!”. Попробуем разобраться в причинах, побудивших написать эти слова.

Практически всему живому на земле присуще воспринимать окружающую среду как непрерывную последовательность фактов, событий. Этим же свойством обладают и люди, с той лишь разницей, что только им дано анализировать поступающую информацию и (хотя и не всем из них это удается) делать выводы из такого анализа и учитывать их в своей сознательной деятельности. Поэтому можно смело утверждать, что во все времена, все люди занимались и занимаются статистическими “исследованиями”, даже не зная иногда такого слова - “статистика”.

Все наши наблюдения над окружающем нас миром можно условно разделить на два класса:

· наблюдения за фактами - событиями, которые могут произойти или не произойти;

· наблюдения за физическими величинами, значения которых в момент наблюдения могут быть различными.

И атеист и верующий в бога человек, скорее всего, согласятся с несколько необычным заявлением - в окружающем нас мире происходят только случайные события, а наблюдаемые нами значения всех показателей внешней среды являются случайными величинами (далее везде – СВ) . Более того, далее будет показано, что иногда можно использовать только одно понятие - случайное событие.

Не задерживаясь на раскрытии философской сущности термина “случайность” (вполне достаточно обычное, житейское представление), обратимся к чрезвычайно важному понятию - вероятность. Этот термин обычно используют по отношению к событию и определяют числом (от 0 до 1), выражающим степень нашей уверенности в том, что данное событие произойдет. События с вероятностью 0 называют невозможными, а события с вероятностью 1 - достоверными (хотя это уже – неслучайные, детерминированные события).

Иногда в прикладной статистике приходится иметь дело с так называемыми редкими (маловероятными) событиями. К ним принято относить события, значение вероятности которых не превышает определенного уровня, чаще всего – 0.05 или 5 %.

В тех случаях, когда профессионалу- статистику приходится иметь дело со случайными величинами, последние часто делят на две разновидности:

· дискретные СВ, которые могут принимать только конкретные, заранее оговоренные значения (например, - значения чисел на верхней грани брошенной игральной кости или порядковые значения текущего месяца);

· непрерывные СВ (чаще всего - значения некоторых физических величин: веса, расстояния, температуры и т.п.), которые по законам природы могут принимать любые значения, хотя бы и в некотором интервале.

Вероятности случайных событий

Итак, основным “показателем” любого события (факта) А является численная величина его вероятности P(A), которая может принимать значения в диапазоне (0…1) - в зависимости от того, насколько это событие случайно. Такое, смысловое, определение вероятности не дает, однако, возможности указать путь для вычисления ее значения.

Поэтому необходимо иметь и другое, отвечающее требованиям практической работы, определение термина “вероятность”. Это определение можно дать на основании житейского опыта и обычного здравого смысла.

Если мы интересуемся событиемA, то, скорее всего, можем наблюдать, фиксировать факты его появления. Потребность в понятии вероятности и ее вычисления возникнет, очевидно, только тогда, когда мы наблюдаем это событие не каждый раз, либо осознаем, что оно может произойти, а может не произойти. И в том и другом случае полезно использовать понятие частоты появления события fA - как отношения числа случаев его появления (благоприятных исходов или частостей) к общему числу наблюдений.

Интуиция подсказывает, что частота наступления случайного события зависит не только от степени случайности самого события. Если мы наблюдали за событием всего пять раз и в трех случаях это событие произошло, то мало кто примет значение вероятности такого события равным 0.6 или 60 %. Скорее всего, особенно в случаях необходимости принятия каких–то важных, дорогостоящих решений любой из нас продолжит наблюдения. Здравый смысл подсказывает нам, что уж если в 100 наблюдениях событие произошло 14 раз, то мы можем с куда большей уверенностью полагать его вероятность равной 14 % .

Таким образом, мы (конечно же, - не первые) сформулировали второе определение понятия вероятности события - как предела, к которому стремится частота наблюдения за событием при непрерывном увеличении числа наблюдений. Теория вероятностей, специальный раздел математики, доказывает существование такого предела и сходимость частоты к вероятности при стремлении числа наблюдений к бесконечности. Это положение носит название центральной предельной теоремы или закона больших чисел.

Итак, первый ответ на вопрос - как найти вероятность события, у нас уже есть. Надо проводить эксперимент и устанавливать частоту наблюдений, которая тем точнее даст нам вероятность, чем больше наблюдений мы имеем.

Ну, а как быть, если эксперимент невозможен (дорог, опасен или меняет суть процессов, которые нас интересуют)? Иными словами, нет ли другого пути вычисления вероятности событий, без проведения экспериментов?

Такой путь есть, хотя, как ни парадоксально, он все равно основан на опыте, опыте жизни, опыте логических рассуждений. Вряд ли кто либо будет производить эксперименты, подбрасывая несколько сотен или тысячу раз симметричную монетку, чтобы выяснить вероятность появления герба при одном бросании! Вы будете совершенно правы, если без эксперимента найдете вероятность выпадения цифры 6 на симметричной игральной кости и т.д., и т.п.

Этот путь называется статистическим моделированием – использованием схемы случайных событий и с успехом используется во многих приложениях теоретической и прикладной статистики. Продемонстрируем этот путь, рассматривая вопрос о вероятностях случайных величин дальше. Обозначим величину вероятности того, что событие A не произойдет. Тогда из определения вероятности через частоту наступления события следует, что

P(A)+ = 1, {1–1}

что полезно читать так - вероятность того, что событие произойдет или не произойдет, равна 100 %, поскольку третьего варианта попросту нет.

Подобные логические рассуждения приведут нас к более общей формуле - сложения вероятностей. Пусть некоторое случайное событие может произойти только в одном из 5 вариантов, т.е. пусть имеется система из трех несовместимых событий A, B и C .

Тогда очевидно, что:

P(A) + P(B) + P(C) = 1; {1–2} и столь же простые рассуждения приведут к выражению для вероятности наступления одного из двух несовместимых событий (например, A или B):

P(AÈ B) = P(A) + P(B); {1–3} или одного из трех:

P(AÈ BÈ C) = P(A) + P(B) + P(C); {1-4} и так далее.

Рассмотрим чуть более сложный пример. Пусть нам надо найти вероятность события C, заключающегося в том, что при подбрасывании двух разных монет мы получим герб на первой (событие A) и на второй (событие B). Здесь речь идет о совместном наступлении двух независимых событий, т.е. нас интересует вероятность P(C) = P(AÇ B).

И здесь метод построения схемы событий оказывается чудесным помощником - можно достаточно просто доказать, что

P(AÇ B) =P(A)· P(B). {1-5} Конечно же, формулы {1-4} и {1-5} годятся для любого количества событий: лишь бы они были несовместными в первом случае и независимыми во втором.

Наконец, возникают ситуации, когда случайные события оказываются взаимно зависимыми. В этих случаях приходится различать условные вероятности:

P(A / B) – вероятность A при условии, что B уже произошло;

P(A / ) – вероятность A при условии, что B не произошло,

называя P(A) безусловной или полной вероятностью события A .

Выясним вначале связь безусловной вероятности события с условными. Так как событие A может произойти только в двух, взаимоисключающих вариантах, то, в соответствии с {1–3} получается, что

P(A) = P(A/B)· P(B) + P(A/)· P(). {1–6}

Вероятности P(A/B) и P(A/) часто называют апостериорными (“a posteriopri” – после того, как…), а безусловную вероятность P(A) – априорной (“a priori” – до того, как…).

Очевидно, что если первым считается событие B и оно уже произошло, то теперь наступление события A уже не зависит от B и поэтому вероятность того, что произойдут оба события составит

P(AÇ B) = P(A/B)· P(B). {1–7} Так как события взаимозависимы, то можно повторить наши выводы и получить

P(B) = P(B/A)· P(A) + P(B/)· P(); {1–8}

а также P(AÇ B) = P(B/A)· P(A). {1–9}

Мы доказали так называемую теорему Байеса

P(A/B)· P(B) = P(B/A)· P(B); {1–10} – весьма важное средство анализа, особенно в области проверки гипотез и решения вопросов управления на базе методов прикладной статистики.

Подведем некоторые итоги рассмотрения вопроса о вероятностях случайных событий. У нас имеются только две возможности узнать что либо о величине вероятности случайного события A:

· применить метод статистического моделирования - построить схему данного случайного события и (если у нас есть основания считать, что мы правильно ее строим) и найти значение вероятности прямым расчетом;

· применить метод статистического испытания - наблюдать за появлением события и затем по частоте его появления оценить вероятность.

На практике приходится использовать оба метода, поскольку очень редко можно быть абсолютно уверенным в примененной схеме события (недостаток метода моделирования) и столь же редко частота появления события достаточно быстро стабилизируется с ростом числа наблюдений (недостаток метода испытаний).

Распределения вероятностей случайных величин Шкалирование случайных величин

Как уже отмечалось, дискретной называют величину, которая может принимать одно из счетного множества так называемых “допустимых” значений. Примеров дискретных величин, у которых есть некоторая именованная единица измерения, можно привести достаточно много.

Прежде всего, надо учесть тот факт что все физические величины (вес, расстояния, площади, объемы и т.д.) теоретически могут принимать бесчисленное множество значений, но практически - только те значения, которые мы можем установить измерительными приборами. А это значит, что в прикладной статистике вполне допустимо распространить понятие дискретных СВ на все без исключения численные описания величин, имеющих единицы измерения.

Вместе с тем надо не забывать, что некоторые СВ просто не имеют количественного описания, естественных единиц измерения (уровень знаний, качество продукции и т. п.).

Покажем, что для решения вопроса о “единицах измерения” любых СВ, с которыми приходится иметь дело в прикладной статистике, достаточно использовать четыре вида шкал.

· Nom. Первой из них рассмотрим так называемую номинальную шкалу — применяемую к тем величинам, которые не имеют природной единицы измерения. В ряде случаев нам приходится считать случайными такие показатели предметов или явлений окружающего нас мира, как марка автомобиля; национальность человека или его пол, социальное положение; цвет некоторого изделия и т.п.

В таких ситуациях можно говорить о случайном событии - "входящий в магазин посетитель оказался мужчиной", но вполне допустимо рассматривать пол посетителя как дискретную СВ, которая приняла одно из допустимых значений на своей номинальной шкале.

Итак, если некоторая величина может принимать на своей номинальной шкале значения X, Y или Z, то допустимыми считаются только выражения типа: X # Y, X=Z , в то время как выражения типа X ³ Z, X + Z не имеют никакого смысла.

· Ord. Второй способ шкалирования – использование порядковых шкал. Они незаменимы для СВ, не имеющих природных единиц измерения, но позволяющих применять понятия предпочтения одного значения другому. Типичный пример: оценки знаний (даже при числовом описании), служебные уровни и т. п. Для таких величин разрешены не только отношения равенства (= или #), но и знаки предпочтения (> или <). Очень часто порядковые шкалы называют ранговыми и говорят о рангах значений таких величин.

· Int. Для СВ, имеющих натуральные размерности (единицы измерения в прямом смысле слова), используется интервальная шкала. Для таких величин, кроме отношений равенства и предпочтения, допустимы операции сравнения – т. е. все четыре действия арифметики. Главная особенность таких шкал заключается в том, что разность двух значений на шкале (36 и 12) имеет один смысл для любого места шкалы (28 и 4). Вместе с тем на интервальной шкале не имеют никакого смысла отрицательные значения, - если это веса предметов, возраст людей и подобные им показатели.

· Rel. Если СВ имеет естественную единицу измерения (например, - температура по шкале Цельсия) и ее отрицательные значения столь же допустимы, как и положительные, то шкалу для такой величины называют относительной.

Методы использования описанных шкал относится к специальному разделу – так называемой непараметрической статистике и обеспечивают, по крайней мере, два неоспоримых преимущества.

· Появляется возможность совместного рассмотрения нескольких СВ совершенно разной природы (возраст людей и их национальная принадлежность, марка телевизора и его стоимость) на единой платформе - положения каждой из величин на своей собственной шкале.

· Если мы сталкиваемся с СВ непрерывной природы, то использование интервальной или относительной шкалы позволит нам иметь дело не со случайными величинами, а со случайными событиями — типа “вероятность того, что вес продукции находится в интервале 17 Кг”. Появляется возможность применения единого подхода к описанию всех интересующих нас показателей при статистическом подходе к явлениям окружающего нас мира.

Законы распределений дискретных случайных величин.

Пусть некоторая СВ является дискретной, т.е. может принимать лишь фиксированные (на некоторой шкале) значения X i. В этом случае ряд значений вероятностей P(X i)для всех (i=1…n) допустимых значений этой величины называют её законом распределения.

В самом деле, - такой ряд содержит всю информацию о СВ, это максимум наших знаний о ней. Другое дело, - откуда мы можем получить эту информацию, как найти закон распределения? Попытаемся ответить на этот принципиально важный вопрос, используя уже рассмотренное понятие вероятности.

Точно также, как и для вероятности случайного события, для закона распределения СВ есть только два пути его отыскания. Либо мы строим схему случайного события и находим аналитическое выражение (формулу) вычисления вероятности (возможно, кто–то уже сделал или сделает это за нас!), либо придется использовать эксперимент и по частотам наблюдений делать какие–то предположения (выдвигать гипотезы) о законе распределения.

Заметим, что во втором случае нас будет ожидать новый вопрос, - а какова уверенность в том, что наша гипотеза верна? Какова, выражаясь языком статистики, вероятность ошибки при принятии гипотезы или при её отбрасывании?

Продемонстрируем первый путь отыскания закона распределения.

Пусть важной для нас случайной величиной является целое число, образуемое по следующему правилу: мы трижды бросаем симметричную монетку, выпадение герба считаем числом 1 (в противном случае 0) и после трех бросаний определяем сумму S.

Ясно, что эта сумма может принимать любое значение в диапазоне 0…3, но всё же - каковы вероятности P(S=0), P(S=1), P(S=2), P(S=3); что можно о них сказать, кроме очевидного вывода - их сумма равна 1?

Попробуем построить схему интересующих нас событий. Обозначим через p вероятность получить 1 в любом бросании, а через q=(1–p) вероятность получить 0. Сообразим, что всего комбинаций ровно 8 (или 23), а поскольку монетка симметрична, то вероятность получить любую комбинацию трех независимых событий (000,001,010…111) одна и та же: q3 = q2· p =…= p3 = 0.125 . Но если p # q , то варианты все тех же восьми комбинаций будут разными:

Таблица 1- 1

Первое бросание	0	0	0	0	1	1	1	1
Второе бросание	0	0	1	1	0	0	1	1
Третье бросание	0	1	0	1	0	1	0	1
Сумма S	0	1	1	2	1	2	2	3
Вероятность P(S)	q3	q2· p	q2· p	q· p2	q2· p	q· p2	q· p2	p3

Запишем то, что уже знаем - сумма вероятностей последней строки должна быть равна единице:

p3 +3· qp2 + 3· q2· p + q3 = (p + q)3 = 1.

Перед нами обычный бином Ньютона 3-й степени, но оказывается - его слагаемые четко определяют вероятности значений случайной величины S !

Мы “открыли” закон распределения СВ, образуемой суммированием результатов n последовательных наблюдений, в каждом из которых может появиться либо 1 (с вероятностью p), либо 0 (с вероятностью 1– p).

Итог этого открытия достаточно скромен:

· возможны всего N = 2 n вариантов значений суммы;

· вероятности каждого из вариантов определяются элементами разложения по

степеням бинома (p + q) n ;

· такому распределению можно дать специальное название - биномиальное.

Конечно же, мы опоздали со своим открытием лет на 300, но, тем не менее, попытка отыскания закона распределения с помощью построения схемы событий оказалась вполне успешной.

В общем случае биномиальный закон распределения позволяет найти вероятность события S = k в виде

P(S=k)=· pk· (1– p)n-k, {2–1} где - т.н. биномиальные коэффициенты, отыскиваемые из известного “треугольника Паскаля” или по правилам комбинаторики - как число возможных сочетаний из n элементов по k штук в каждом:

= n· (n –1)· ...· (n – k + 1)/ (1· 2· .... · k). {2–2}

Многие дискретные СВ позволяют построить схему событий для вычисления вероятности каждого из допустимых для данной случайной величины значений.

Конечно же, для каждого из таких, часто называемых "классическими", распределений уже давно эта работа проделана – широко известными и очень часто используемыми в прикладной статистике являются биномиальное и полиномиальное распределения, геометрическое и гипергеометрическое, распределение Паскаля и Пуассона и многие другие.

Для почти всех классических распределений немедленно строились и публиковались специальные статистические таблицы, уточняемые по мере увеличения точности расчетов. Без использования многих томов этих таблиц, без обучения правилам пользования ими последние два столетия практическое использование статистики было невозможно.

Сегодня положение изменилось – нет нужды хранить данные расчетов по формулам (как бы последние не были сложны!), время на использование закона распределения для практики сведено к минутам, а то и секундам.

Уже сейчас существует достаточное количество разнообразных пакетов прикладных компьютерных программ для этих целей. Кроме того, создание программы для работы с некоторым оригинальным, не описанным в классике распределением не представляет серьезных трудностей для программиста “средней руки”.

Приведем примеры нескольких распределений для дискретных СВ с описанием схемы событий и формулами вычисления вероятностей. Для удобства и наглядности будем полагать, что нам известна величина p – вероятность того, что вошедший в магазин посетитель окажется покупателем и обозначая (1– p) = q.

· Биномиальное распределение

Если X – число покупателей из общего числа n посетителей, то вероятность P(X= k) = · pk· qn-k .

· Отрицательное биномиальное распределение (распределение Паскаля)

Пусть Y – число посетителей, достаточное для того, чтобы k из них оказались покупателями. Тогда вероятность того, что n–й посетитель окажется k–м покупателем составит P(Y=n)=· pk · qn–k.

· Геометрическое распределение

Если Y – число посетителей, достаточное для того, чтобы один из них оказался

покупателем, то P(Y=1)= p · qn–1.

· Распределение Пуассона

Если ваш магазин посещают довольно часто, но при этом весьма редко делают покупки, то вероятность k покупок в течение большого интервала времени, (например, – дня) составит P(Z=k) = l k · Exp(-l ) / k! , где l – особый показатель распределения, так называемый его параметр.

Односторонние и двухсторонние значения вероятностей

Если нам известен закон распределения СВ (пусть – дискретной), то в этом случае очень часто приходится решать задачи, по крайней мере, трех стандартных типов:

· какова вероятность того, что случайная величина X окажется равной (или наоборот – не равной) некоторому значению, например – Xk ?

· какова вероятность того, что случайная величина X окажется больше (или наоборот – меньше) некоторого значения, например –Xk ?

· какова вероятность того, что случайная величина X окажется не меньше Xi и при этом не больше Xk ?

Первую вероятность иногда называют "точечной", ее можно найти из закона распределения, но только для дискретной случайной величины. Разумеется, что вероятность равенства задана самим законом распределения, а вероятность неравенства составляет

P(X#Xk) = 1 – P(X=Xk).

Вторую вероятность принято называть "односторонней". Вычислять ее также достаточно просто – как сумму вероятностей всех допустимых значений, равных и меньших Xk . Для примера "открытого" нами закона биномиального распределения при p=0.5 и m=4 одностороння вероятность того, что X окажется менее 3 (т.е.0, 1 или 2), составит точно 0.0625+0.25+0.375=0.6875.

Вероятность третьего типа называют "двухсторонней" и вычисляют как сумму вероятностей значений X внутри заданного интервала. Для предыдущего примера вероятность того, что X менее 4 и более 1 составит 0.375+0.25=0.625.

Односторонняя и двухсторонняя вероятности являются универсальными понятиями – они применимы как для дискретных, так и для непрерывных случайных величин.

Моменты распределений дискретных случайных величин.

Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней и большего желать не приходится.

Не будет лишним помнить, что этот закон (или просто – распределение случайной величины) можно задать тремя способами:

· в виде формулы: например, для биномиального распределения при n=3 и p=0.5 вероятность значения суммы S=2 составляет 0.375;

· в виде таблицы значений величины и соответствующих им вероятностей:

· в виде диаграммы или, как ее иногда называют, гистограммы распределения:

Таблица 2–1

Сумма	0	1	2	3
Вероятность	0.125	0.375	0.375	0.125

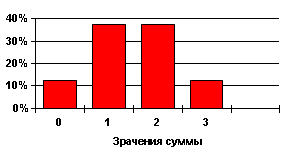
Рис. 2–1 Гистограмма распределения

Необходимость рассматривать вопрос, поставленный в заглавии параграфа, не так уж и очевидна, поскольку непонятно, что же еще нам надо знать?

Между тем, все достаточно просто. Пусть, для какого–то реального явления или процесса мы сделали допущение (выдвинули гипотезу), что соответствующая СВ принимает свои значения в соответствии с некоторой схемой событий. Рассчитать вероятности по принятой нами схеме – не проблема!

Вопрос заключается в другом – как проверить свое допущение или, на языке статистики, оценить достоверность гипотезы?

По сути дела, кроме обычного наблюдения за этой СВ у нас нет иного способа выполнить такую проверку. И потом – в силу самой природы СВ мы не можем надеяться, что через достаточно небольшое число наблюдений их частоты превратятся в “теоретические” значения, в вероятности. Короче – результат наблюдения над случайной величиной тоже … случайная величина или, точнее, – множество случайных величин.

Так или примерно так рассуждали первые статистики–профессионалы. И у кого–то из них возникла простая идея: сжать информацию о результатах наблюдений до одного, единственного показателя!

Как правило, простые идеи оказываются предельно эффективными, поэтому способ оценки итогов наблюдений по одному, желательно “главному”, “центральному” показателю пережил все века становления прикладной статистики и по ходу дела обрастал как теоретическими обоснованиями, так и практическими приемами использования.

Вернемся к гистограмме рис. 2–1 и обратим внимание на два, бросающихся в глаза факта:

· “наиболее вероятными” являются значения суммы S=1 и S=2 и эти же значения лежат “посредине” картинки;

· вероятность того, что сумма окажется равной 0 или 1, точно такая же, как и вероятность 2 или 3, причем это значение вероятности составляет точно 50 %.

Напрашивается простой вопрос – если СВ может принимать значения 0, 1, 2 или 3, то сколько в среднем составляет ее значение или, иначе – что мы ожидаем, наблюдая за этой величиной?

Ответ на такой вопрос на языке математической статистики состоит в следующем. Если нам известен закон распределения, то, просуммировав произведения значений суммы S на соответствующие каждому значению вероятности, мы найдем математическое ожидание этой суммы как дискретной случайной величины –

M(S) = S S i · P(S i). {2–3}

В рассматриваемом нами ранее примере биномиального распределения, при значении p=0.5, математическое ожидание составит

M(S) = 0· 0.125+1· 0.375+2· 0.375+3· 0.125= 1.5 .

Обратим внимание на то, что математическое ожидание дискретной величины типа Int или Rel совсем не обязательно принадлежит к множеству допустимых ее значений. Что касается СВ типа Nom или Ord, то для них понятие математического ожидания (по закону распределения), конечно же, не имеет смысла. Но так как с номинальной, так и с порядковой шкалой дискретных СВ приходится иметь дело довольно часто, то в этих случаях прикладная статистика предлагает особые, непараметрические методы.

Продолжим исследование свойств математического ожидания и попробуем в условиях нашего примера вместо S рассматривать U= S – M(S). Такая замена СВ (ее часто называют центрированием) вполне корректна: по величине U всегда можно однозначно определить S и наоборот.

Если теперь попробовать найти математическое ожидание новой (не обязательно дискретной) величины M(U) , то оно окажется равным нулю, независимо от того считаем ли мы конкретный пример или рассматриваем такую замену в общем виде.

Мы обнаружили самое важное свойство математического ожидания – оно является “центром” распределения. Правда, речь идет вовсе не о делении оси допустимых значений самой СВ на две равные части. Поистине – первый показатель закона распределения “самый главный” или, на языке статистики, – центральный.

Итак, для СВ с числовым описанием математическое ожидание имеет достаточно простой смысл и легко вычисляется по законам распределения. Заметим также, что математическое ожидание – просто числовая величина (в общем случае не дискретная, а непрерывная) и никак нельзя считать ее случайной.

Другое дело, что эта величина зависит от внутренних параметров распределения (например, – значения вероятности р числа испытаний n биномиальном законе).

Так для приведенных выше примеров дискретных распределений математическое ожидание составляет:

Тип распределения	Математическое ожидание
Биномиальное	n· p
Распределение Паскаля	k · q / p
Геометрическое распределение	q / p
Распределение Пуассона	l

Возникает вопрос – так что же еще надо? Ответ на этот вопрос можно получить как из теории, так и из практики.

Один из разделов кибернетики – теория информации (курс “Основы теории информационных систем” у нас впереди) в качестве основного положения утверждает, что всякая свертка информации приводит к ее потере. Уже это обстоятельство не позволяет допустить использование только одного показателя распределения СВ – ее математического ожидания.

Практика подтверждает это. Пусть мы построили (или использовали готовые) законы распределения двух случайных величин X и Y и получили следующие результаты:

Таблица 2–2

Значения	1	2	3	4
P(X) %	12	38	38	12
P(Y) %	30	20	20	30

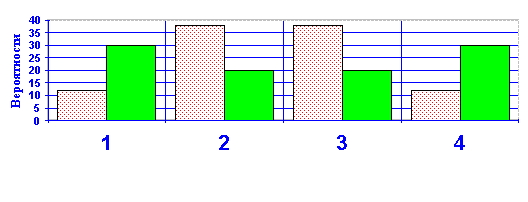
Рис. 2–2

Простое рассмотрение табл.2–2 или соответствующих гистограмм рис.2–2 приводит к выводу о равенстве M(X) = M(Y) = 0.5 , но вместе с тем столь же очевидно, что величина X является заметно “менее случайной”, чем Y.

Приходится признать, что математическое ожидание является удобным, легко вычислимым, но весьма неполным способом описания закона распределения. И поэтому требуется еще как–то использовать полную информацию о случайной величине, свернуть эту информацию каким–то иным способом.

Обратим внимание, что большие отклонения от M(X) у величины X маловероятны, а у величины Y – наоборот. Но при вычислении математического ожидания мы, по сути дела “усредняем” именно отклонения от среднего, с учетом их знаков. Стоит только “погасить” компенсацию отклонений разных знаков и сразу же первая СВ действительно будет иметь показатель разброса данных меньше, чем у второй. Именно такую компенсацию мы получим, усредняя не сами отклонения от среднего, а квадраты этих отклонений.

Соответствующую величину

D(X) = S (X i – M(X))2 · P(X i); {2–4} принято называть дисперсией распределения дискретной СВ.

Ясно, что для величин, имеющих единицу измерения, размерность математического ожидания и дисперсии оказываются разными. Поэтому намного удобнее оценивать отклонения СВ от центра распределения не дисперсией, а квадратным корнем из нее – так называемым среднеквадратичным отклонением s , т.е. полагать

s 2 = D(X). {2–5}

Теперь оба параметра распределения (его центр и мера разброса) имеют одну размерность, что весьма удобно для анализа.

Отметим также, что формулу {2–3} часто заменяют более удобной

D(X) = S (X i)2 · P(X i) – M(X)2. {2–6}

Весьма полезно будет рассмотреть вопрос о предельных значениях дисперсии.

Подобный вопрос был бы неуместен по отношению к математическому ожиданию – мало ли какие значения может иметь дискретная СВ, да еще и со шкалой Int или Rel.

Но дословный перевод с латыни слова “дисперсия” означает “рассеяние”, “разброс” и поэтому можно попытаться выяснить – чему равна дисперсия наиболее или наименее “разбросанной” СВ? Скорее всего, наибольший разброс значений (относительно среднего) будет иметь дискретная случайная величина X, у которой все n допустимых значений имеют одну и ту же вероятность 1/n. Примем для удобства Xmin и Xmax (пределы изменения данной величины), равными 1 и n соответственно.

Математическое ожидание такой, равномерно распределенной случайной величины составит M(X) = (n+1)/2 и остается вычислить дисперсию, которая оказывается равной D(X) = S (Xi)2/n – (n+1)2/4 = (n2–1)/ 12.

Можно доказать, что это наибольшее значение дисперсии для дискретной СВ со шкалой Int или Rel .

Последнее выражение позволяет легко убедиться, что при n =1 дисперсия оказывается равной нулю – ничего удивительного: в этом случае мы имеем дело с детерминированной, неслучайной величиной.

Дисперсия, как и среднеквадратичное отклонение для конкретного закона распределения являются просто числами, в полном смысле показателями этого закона.

Полезно познакомиться с соотношениями математических ожиданий и дисперсий для упомянутых ранее стандартных распределений:

Таблица 2–3

Тип распределения	Математическое ожидание	Дисперсия	Коэффициент вариации
Биномиальное	np	npq	Sqrt(q/n· p)
Паскаля	kq/p	kq/p2	Sqrt(1/ kq)
Геометрическое	q/p	q/p2	Sqrt(1/q)
Пуассона	l	l	Sqrt(1/l )

Можно ли предложить ещё один или несколько показателей – сжатых описаний распределения дискретной СВ? Разумеется, можно.

Первый показатель (математическое ожидание) и второй (дисперсия) чаще всего называют моментами распределения. Это связано со способами вычисления этих параметров по известному закону распределения – через усреднение значений самой СВ или усреднение квадратов ее значений.

Конечно, можно усреднять и кубы значений, и их четвертые степени и т.д., но что мы при этом получим? Поищем в теории ответ и на эти вопросы.

Начальными моментами k-го порядка случайной величины X обычно называют суммы:

n k = S (X i)k · P(X i); n 0 = 0; {2–7}

а центральными моментами – суммы:

m k= S (X i –n 1)k · P(X i), {2–8} при вычислении которых усредняются отклонения от центра распределения – математического ожидания.

Таким образом,

· m 1 = 0;

· n 1 = M(X) является параметром центра распределения;

· m 2 = D(X) является параметром рассеяния; {2-9}

· n 3 и m 3 – описывают асимметрию распределения;.

· n 4 и m 4 – описывают т.н. эксцесс (выброс) распределения и т.д.

Иногда используют еще один показатель степени разброса СВ – коэффициент вариации V= s / M(X), имеющий смысл при ненулевом значении математического ожидания.

Распределения непрерывных случайных величин

До этого момента мы ограничивались только одной “разновидностью” СВ – дискретными, т.е. принимающими конечные, заранее оговоренные значения на любой из шкал Nom, Ord, Int или Rel .

Но теория и практика статистики