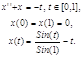Краевые задачи и разностные схемы
Реферат з курсу “Введение в численные методы”
Тема: “КРАЕВЫЕ ЗАДАЧИ И РАЗНОСТНЫЕ СХЕМЫ”
Содержание
1. Приведение к системе уравнений первого порядка
2. Разностное представление систем дифференциальных уравнений
3. Разностные системы уравнений для краевых задач
4. Краевые задачи второго порядка
5. Разностные схемы для уравнений в частных производных
6. Повышение точности разностных схем
7. Сеточные методы для нестационарных задач
Литература
1. Приведение к системе уравнений первого порядка
Для решения систем дифференциальных уравнений высокого порядка методами конечных разностей в первую очередь возникает потребность преобразования исходной системы в систему дифференциальных уравнений первого порядка с соответствующим образом преобразованными начальными или граничными условиями. И уже далее реализовывать численную процедуру решения.
Преобразование в систему уравнений первого порядка не единственно. Наиболее популярные из них в большинстве своем касаются линейных систем с постоянными или переменными коэффициентами. Основная идея всех методов состоит во введении новых переменных и выполнении замены высших производных этими переменными.
Пусть неоднородное дифференциальное уравнение высокого порядка задано в виде:
![]()
где ![]() – соответственно i-тая производная искомого решения и ее значение в начальный момент,
– соответственно i-тая производная искомого решения и ее значение в начальный момент,
![]() – функция, описывающая внешнее воздействие на динамический объект.
– функция, описывающая внешнее воздействие на динамический объект.
Обозначим первую производную искомой функции новой переменной ![]() , первую производную
, первую производную ![]() – следующей переменной:
– следующей переменной: ![]() , первую производную
, первую производную ![]() – переменной
– переменной ![]() и т.д.. Таким образом из исходной системы мы сформируем
и т.д.. Таким образом из исходной системы мы сформируем ![]() дифференциальное уравнение первого порядка:
дифференциальное уравнение первого порядка:
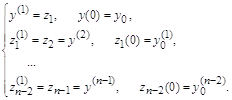
При таких заменах производных искомой функции ![]() ее -ная производная оказывается равной первой производной от
ее -ная производная оказывается равной первой производной от ![]() :
:
![]()
В результате, эквивалентная система дифференциальных уравнений первого порядка примет следующий вид:
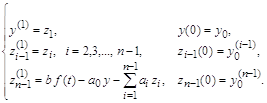
В случае, когда правая часть представлена взвешенной суммой функции ![]() и ее производных и в целом дифференциальное уравнение имеет вид
и ее производных и в целом дифференциальное уравнение имеет вид
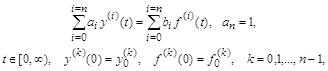
то его преобразование в систему уравнений первого порядка с новыми переменными ![]() осуществляется по следующим формулам:
осуществляется по следующим формулам:
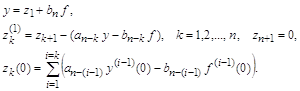
Такое преобразование сохраняет коэффициенты исходного уравнения неизменными и исключает производные в правой части от ![]() . Начальные условия для новых переменных здесь приходится пересчитывать по достаточно сложным соотношениям.
. Начальные условия для новых переменных здесь приходится пересчитывать по достаточно сложным соотношениям.
И, наконец, приведем еще один вариант разложения на систему уравнений первого порядка исходного неоднородного уравнения с производными в правой части:
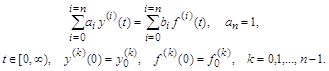
Замена переменных в отличие от предыдущего случая производится без сохранения коэффициентов исходного уравнения:
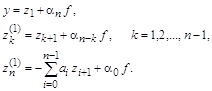
Производные искомой функции ![]() можно выразить через вновь введенные переменные
можно выразить через вновь введенные переменные ![]() путем многократного дифференцирования левой и правой части соотношения для y с подстановкой после каждого дифференцирования производных
путем многократного дифференцирования левой и правой части соотношения для y с подстановкой после каждого дифференцирования производных ![]() :
:
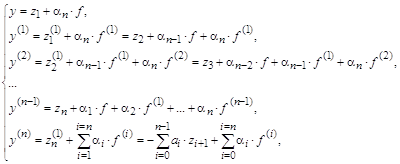
Умножив каждое выражение для ![]() на коэффициенты
на коэффициенты ![]() и просуммировав правые и левые члены равенств, получим уравнение, которое отличается от исходного лишь коэффициентами при производных в правых частях. Чтобы добиться тождественности, необходимо коэффициенты при соответствующих производных приравнять и разрешить полученную систему уравнений относительно неизвестных
и просуммировав правые и левые члены равенств, получим уравнение, которое отличается от исходного лишь коэффициентами при производных в правых частях. Чтобы добиться тождественности, необходимо коэффициенты при соответствующих производных приравнять и разрешить полученную систему уравнений относительно неизвестных ![]() .
.
Система уравнений имеет вид:
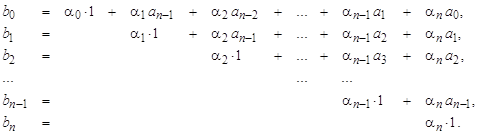
В векторно-матричной форме это уравнение и его решение записываются в следующем виде:
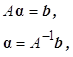
где ![]() – вектор известных коэффициентов,
– вектор известных коэффициентов,
![]() – вектор искомых коэффициентов,
– вектор искомых коэффициентов,
![]() – соответственно прямая и обратная верхне-треугольные матрицы коэффициентов. Первая из них выглядит так:
– соответственно прямая и обратная верхне-треугольные матрицы коэффициентов. Первая из них выглядит так:
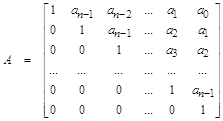 .
.
Обратная матрица удобна при использовании математических пакетов для решения векторно-матричного уравнения. Если ![]() , то коэффициенты
, то коэффициенты ![]() легко вычисляются последовательной подстановкой значений
легко вычисляются последовательной подстановкой значений ![]() , начиная с
, начиная с ![]() .
.
Начальные условия для ![]() вычисляются по выражениям для
вычисляются по выражениям для ![]() следующим образом:
следующим образом:
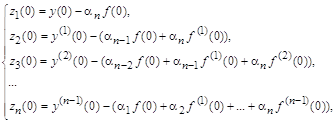
или в векторно-матричной форме:
![]() ,
,
![]()
![]()
![]()
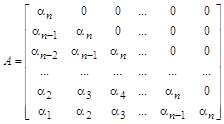 .
.
2. Разностное представление систем дифференциальных уравнений
Представление системы дифференциальных уравнений первого порядка с начальными условиями
![]()
можно заменить системой конечно-разностных уравнений первого порядка с целочисленной независимой переменной i (![]() ):
):
![]() ,
,
погрешность аппроксимации которого пропорциональна сеточному шагу h.
Выше было уже показано, как можно уменьшить погрешность аппроксимации, делая ее пропорциональной ![]() . В частности это можно сделать, использовав среднее арифметическое двух разностей первого порядка: “вперед” и “ назад”.
. В частности это можно сделать, использовав среднее арифметическое двух разностей первого порядка: “вперед” и “ назад”.
![]()
При такой замене производной мы получаем систему разностных уравнений, состоящую из разностных уравнений второго порядка, требующих, кроме известного вектора начальных условий ![]() , еще один дополнительный вектор
, еще один дополнительный вектор ![]() :
:
![]() .
.
Дополнительный вектор начальных условий достаточно вычислить по формуле Эйлера. Он и определит дополнительное начальное условие с ошибкой, пропорциональной второй степени h:
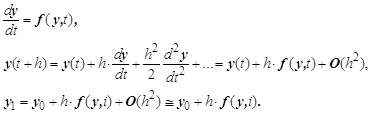
Подстановка таких начальных условий в решение сохранит погрешность результатов на уровне ![]() . В таком случае говорят, что разностная схема имеет второй порядок точности.
. В таком случае говорят, что разностная схема имеет второй порядок точности.
3. Разностные системы уравнений для краевых задач
Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых функции и/или ее производных в различных точках интервала интегрирования и, в частности - на концах интервала. Такого рода уравнения в обыкновенных производных или системы из таких уравнений называются краевой задачей.
Общим методом решения краевой задачи является преобразование ее в систему алгебраических уравнений относительно множества неизвестных значений искомой функции, выбранных в точках, равномерно расположенных на оси абсцисс, т.е. заданных на сетке известных значений независимой переменной.
Для линейной системы уравнений первого порядка, записанной в матричной форме относительно вектора ![]() как
как
![]() ,
,
обязательно задается полный набор краевых условий ![]() , включающий хотя бы одно значение
, включающий хотя бы одно значение ![]() , или набор комбинаций из значений
, или набор комбинаций из значений ![]() и
и ![]()
Обычно задаваемое граничное значение совмещается с тем или иным n-ным сеточным значением независимой переменной. Это позволяет обходиться без преобразования граничных условий к ближайшей точке сетки. Векторы ![]() ,
, ![]() ,
, ![]() и матрица
и матрица ![]() в общем случае приводятся к единичному интервалу изменения независимой переменной с помощью линейного преобразования
в общем случае приводятся к единичному интервалу изменения независимой переменной с помощью линейного преобразования ![]() , в котором
, в котором ![]() с шагом по оси абсцисс равном
с шагом по оси абсцисс равном ![]() . Благодаря этому производные в левых частях единообразно заменяются (M+1)-точечными конечно-разностными выражениями через искомые значения решения:
. Благодаря этому производные в левых частях единообразно заменяются (M+1)-точечными конечно-разностными выражениями через искомые значения решения:
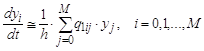 .
.
Многоточечные представления производных получаются путем применения существующих соотношений между операторами дифференцирования, конечных разностей и сдвига:
![]()
Чтобы выразить значение производной порядка k в m-той точке целочисленного интервала (0, ) через ординаты функции ![]() необходимо выполнить следующие операторные преобразования:
необходимо выполнить следующие операторные преобразования:
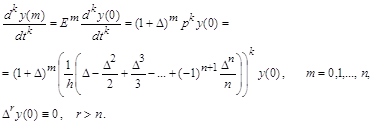
Заменив конечно-разностные операторы ![]() (после приравнивания нулю разностей со степенями выше ) выражениями с оператором сдвига
(после приравнивания нулю разностей со степенями выше ) выражениями с оператором сдвига ![]() и вспомнив, что
и вспомнив, что ![]() , получим в результате для k-той производной в m-той точке взвешенную сумму из ординат искомой функции:
, получим в результате для k-той производной в m-той точке взвешенную сумму из ординат искомой функции:
![]() .
.
Погрешность аппроксимации дифференциального оператора конечно-разностным оператором для центральной точки (m=n/2) пропорциональна с наименьшим коэффициентом величине ![]() и c наибольшим – для точек конца интервала.
и c наибольшим – для точек конца интервала.
Часто применяемые выражения конечно-разностной аппроксимации производных первого и второго порядков по трем-семи равномерно расположенным точкам приведены ниже в таблицах в виде коэффициентов, стоящих перед соответствующими ординатами функции. В левом верхнем углу таблиц записан общий множитель, а в крайней правой колонке – коэффициенты k1, k2для формул погрешности.
Трех точечная аппроксимация первой производной
| y(0) | y(1) | y(2) |
|
y’(0) | -3 | 4 | -1 | 2 |
y’(1) | -1 | 0 | 1 | -1 |
y’(2) | 1 | -4 | 3 | 2 |
Четырех точечная аппроксимация первой производной
|
|
|
|
|
|
| -11 | 18 | -9 | 2 | -3 |
| -2 | -3 | 6 | -1 | 1 |
| 1 | -6 | 3 | 2 | -1 |
| -2 | 9 | -18 | 11 | 3 |
Пятиточечная аппроксимация первой производной
|
|
|
|
|
|
|
| -25 | 48 | -36 | 16 | -3 | 12 |
| -3 | -10 | 18 | -6 | 1 | -3 |
| 1 | -8 | 0 | 8 | -1 | 2 |
| -1 | 6 | -18 | 10 | 3 | -3 |
| 3 | -16 | 36 | -48 | 25 | 12 |
Шести точечная аппроксимация первой производной
|
|
|
|
|
|
|
|
| -137 | 300 | -300 | 200 | -75 | 12 | -10 |
| -12 | -65 | 120 | -60 | 20 | -3 | 2 |
| 3 | -30 | -20 | 60 | -15 | 2 | -1 |
| -2 | 15 | -60 | 20 | 30 | -3 | 1 |
| 3 | -20 | 60 | -120 | 65 | 12 | -2 |
| -12 | 75 | -200 | 300 | -300 | 137 | 10 |
Семи точечная аппроксимация первой производной
|
|
|
|
|
|
|
|
|
| -147 | 360 | -450 | 400 | -225 | 72 | -10 | 60 |
| -10 | -77 | 150 | -100 | 50 | -15 | 2 | -10 |
| 2 | -24 | -35 | 80 | -30 | 8 | -1 | 4 |
| -1 | 9 | -45 | 0 | 45 | -9 | 1 | -3 |
| 1 | -8 | 30 | -80 | 35 | 24 | -2 | 4 |
| -2 | 15 | -50 | 100 | -150 | 77 | 10 | -10 |
| 10 | -72 | 225 | -400 | 450 | -360 | 147 | 60 |
Трех точечная аппроксимация второй производной
|
|
|
|
|
| 1 | -2 | 1 | -12 , 2 |
| 1 | -2 | 1 | 0 , -1 |
| 1 | -2 | 1 | 12 , -2 |
Четырех точечная аппроксимация второй производной
|
|
|
|
|
|
| 2 | -5 | 4 | -1 | 55 , -6 |
| 1 | -2 | 1 | 0 | -5 , -2 |
| 0 | 1 | -2 | 1 | -5 , -2 |
| -1 | 4 | -5 | 2 | 55 , -6 |
Пятиточечная аппроксимация второй производной
|
|
|
|
|
|
|
| 35 | -104 | 114 | -56 | 11 | -150 , 12 |
| 11 | -20 | 6 | 4 | -1 | 15 , -3 |
| -1 | 16 | -30 | 16 | -1 | 0 , 2 |
| -1 | 4 | 6 | -20 | 11 | 15 , 3 |
| 11 | -56 | 114 | -104 | 35 | 150 , -12 |
Шести точечная аппроксимация второй производной
|
|
|
|
|
|
|
| 225 | -770 | 1070 | -780 | 305 | -50 |
| 50 | -75 | -20 | 70 | -30 | 5 |
| -5 | 80 | -150 | 80 | -5 | 0 |
| 0 | -5 | 80 | -150 | 80 | -5 |
| 5 | -30 | 70 | -20 | -75 | 50 |
| -50 | 305 | -780 | 1070 | -770 | 225 |
Семи точечная аппроксимация второй производной
|
|
|
|
|
|
|
|
| 812 | -3132 | 5265 | -5080 | 2970 | -972 | 137 |
| 137 | -147 | -255 | 470 | -285 | 93 | -13 |
| -13 | 228 | -420 | 200 | 15 | -12 | 2 |
| 2 | -27 | 270 | -490 | 270 | -27 | 2 |
| 2 | -12 | 15 | 200 | -420 | 228 | -13 |
| -13 | 93 | -285 | 470 | -255 | -147 | 137 |
| 137 | -972 | 2970 | -5080 | 5265 | -3132 | 812 |
Например, производная первого порядка ![]() в точках m=0, 3, 5 для семи точечной аппроксимации будет иметь вид:
в точках m=0, 3, 5 для семи точечной аппроксимации будет иметь вид:
![]()
![]()
![]() ,
,
![]() .
.
Аналогично выписываются выражения и для вторых производных в точках 0 и 2:
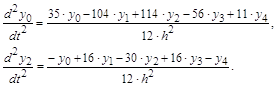
Таким образом, из приведенных таблиц можно выбрать аппроксимирующие выражения для производной в данной точке, включающие значения функции в точках нужного окружения.
4. Краевые задачи для уравнений второго порядка
При математическом описании реальных физических объектов чаще всего приходится иметь дело с дифференциальными уравнениями в обыкновенных или частных производных второго порядка с начальными, краевыми или граничными условиями.
Преобразование их в конечно-разностную систему алгебраических уравнений осуществляется аналогично: для каждой точки в области (интервале) интегрирования, где не задано краевое или граничное значение искомой функции, записывается исходное уравнение, в котором все производные выражены через заранее определенное число близлежащих ординат искомой функции, принадлежащих области, и вычислены все коэффициенты и функции независимых переменных в этой точке. К полученным таким образом уравнениям добавляются соотношения или значения функции и ее производных в точках границы области. В результате будет сформирована алгебраическая система уравнений с числом уравнений и неизвестных, равном общему числу точек области интегрирования.
В процессе формирования уравнений особое внимание необходимо обращать на замену производных конечно-разностными эквивалентами в приграничных точках. В выражениях последних должны отсутствовать неизвестные значения функции в точках, расположенных вне области интегрирования. Это достигается многократным применением оператора сдвига к соответствующему конечно-разностному оператору.
Если в центральных точках точность аппроксимации производных с точками удовлетворяет поставленным требованиям и эту точность желательно сохранить и в приграничных точках заданных областей, то для последних выбирают аппроксимирующие формулы, построенные для (+1)-й точки или более.
Рассмотрим примеры аппроксимации дифференциальных уравнений с краевыми условиями конечно-разностной системой алгебраических уравнений. Эти аппроксимации в литературе получили название "разностные схемы". Ниже в четырех таблицах приведены четыре варианта конечно-разностной аппроксимации одной и той же краевой задачи, для которой известно точное решение. Вид уравнения, условия на границе интервала, решение аналитическое и вычисленное в заданных точках с 12 значащими цифрами приведены в правой крайней колонке первой таблицы. В левых колонках первой и в трех остальных таблицах записаны системы алгебраических уравнений, полученных применением трех-, пяти-, пяти-шести- и семи точечной аппроксимации второй производной в заданном уравнении. Справа от уравнений приведены решения алгебраических уравнений тоже с 12-ю значащими цифрами.
| Система уравнений с трехточечным представлением производных | Вектор разностного решения с шагом h=0.1 |
|
-199 | 0.0186590989712 | 0.0186415437361 |
100 | 0.0361316064473 | 0.0360976603850 |
100 | 0.0512427953890 | 0.0511947672548 |
100 | 0.0628415300546 | 0.0627828520998 |
100 | 0.0698118753674 | 0.0697469636621 |
100 | 0.0710840847137 | 0.0710183518969 |
100 | 0.0656455142231 | 0.0655851465687 |
100 | 0.0525504484304 | 0.0525024675253 |
100 | 0.0309298757856 | 0.0309018656257 |
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Кратные интегралы
- Критерии согласия
В данной курсовой работе рассказано о наиболее распространенных критериях согласия – омега-квадрат, хи-квадрат, Колмогорова и Колмогор
- Математика
- Математика в современном мире
- Математика и золотое сечение
- Математические основы системы остаточных классов
Задача 1. Элементы теории графовСвязный ориентированный граф G (Х, Г) задан множеством вершин X={x1, x2,…,xn} и отображением Гxi={x|I±k|,x|I±l|},i =1, 2,…,
- Математическое моделирование технических объектов
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.