Скачать

Колебания кристаллической решетки

СОДЕРЖАНИЕ

Введение. 2

Глава 1. Колебания кристаллической решетки. 3

1.1.Одномерная цепочка с одним атомом в ячейке. 4

1.2.Одномерная цепочка с двумя атомами в примитивной ячейке. 11

1.3. Трехмерный кристалл. 13

Глава 2. Фононы. Фононный газ. 16

Глава 3. Акустическая и оптическая ветки колебаний. 19

Решение со знаком ''минус'' 19

Решение со знаком ''плюс''. 22

Глава 4. Энергия колебаний и теплоемкость кристаллической решетки. 26

4.1. Модель Эйнштейна. 27

4.2. Модель Дебая. 27

Выводы.. 34

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.. 35

Введение

Одной из важных и сложных задач теории твердого тела является расчет теплоемкости и теплопроводности твердого тела. Для твердых тел в рамках классической механики были получены значения теплоемкости, которые лишь приблизительно были равны реальным значениям теплоемкости при нормальных температурах. При повышенных температурах и при температурах следующих к абсолютному нулю значения теплоемкости оказались зависимы от температуры, чего классическая теория объяснить не могла. Лишь использование квантовой теории смогло объяснить эту зависимость.

Для нахождения величин теплоемкости и теплопроводности твердых кристаллических тел в широком температурном диапазоне вводят понятие фононов – квазичастиц, которые распространяются в твердом теле.

К данной работе мы рассмотрим явления колебаний кристаллической решетки, которые и являются фононами и их виды в зависимости от строения вещества. Также рассмотрим процессы рассеивания с участием акустических и оптических фононов.

Глава 1. Колебания кристаллической решетки

Кристаллическая структура – равновесное состояние системы атомов, отвечающее минимуму потенциальной энергии. В состоянии покоя сумма сил, действующих на каждый атом кристалла со стороны других атомов, равна нулю.

Если вывести эту систему из положения равновесия, в кристалле возникнут сложные колебания. Эти колебания, в частности, всегда имеются при конечной температуре, когда кристаллическая структура обладает определенной (тепловой) энергией, то есть не находится в состоянии статического равновесия.

Рассмотрим колебания решетки в рамках классической механики.

При смещении атома относительно других атомов кристалла возникает сила, стремящаяся вернуть его в равновесное положение. Если смещения невелики, мы можем разложить зависимость силы от смещений в ряд и ограничится линейными по смещениям членами. Тогда колебания кристаллической решетки будут линейными, то есть будут описываться системой линейных дифференциальных уравнений.

Такая система уравнений обладает важным свойством: если есть несколько решений, то их сумма также является решением и сумма двух возможных колебаний – тоже колебание.

Эта система может быть решена, если известна зависимость силы, действующей на атом, от его смещения, а основные характеристики линейных колебаний могут быть предсказаны на основании одних только свойств симметрии кристалла.

Чтобы показать главные черты линейных колебаний кристаллической решетки, мы рассмотрим простейший случай одномерного кристалла – одномерную цепочку атомов.

1.1 Одномерная цепочка с одним атомом в ячейке

Рассмотрим одномерную периодическую цепочку атомов – одномерный кристалл с одним атомом в элементарной ячейке. Пусть период этой цепочки равен a. Тогда в состоянии равновесия координата -го атома цепочки x_n равна na.

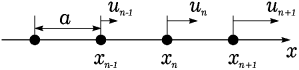
Рис. 1.1. Одномерная цепочка с одним атомом в элементарной ячейке.

Обозначим через u_n смещение -го атома из положения равновесия. Будем считать, что атомы взаимодействуют только с ближайшими соседями. Сила, с которой (+1)–й атом действует на -й зависит от разности смещений этих двух атомов u_n+1–u_n. При небольших смещениях эту силу можно считать пропорциональной разности смещений: F_n,+1 = γ(u_n+1–u_n), где γ – коэффициент пропорциональности. Удобно представить, что атомы связаны друг с другом пружинками с жесткостью γ.

На рис.1.1 пружинка между -м и +1 -м атомами растянута, так что она действует на -й атом в положительном направлении. Растянутая пружинка между –1-м и -м атомом действует на -й атом в отрицательном направлении: F_n,–1 = –γ(x_n–x_n–1).

Запишем закон Ньютона для -го атома цепочки:

(1).

Первое слагаемое в правой части – сила, действующая на -й атом со стороны +1-го атома, второе – сила, действующая со стороны –1-го атома.

После упрощения получим:

(2).

Система таких уравнений, записанных для каждого атома, полностью описывает колебания цепочки.

Если рассматривать только длинноволновые колебания, т. е. колебания с длиной волны много большей периода цепочки a, то можно заменить разность u_n+1–u_n на (∂ u_n/∂ x)a, а величину, стоящую в правой части (2) – на γ a²(∂² u/∂ x²). В результате получим волновое уравнение:

(3).

Решением которого являются волны u = Aexp(ikx–iω t) с линейным законом дисперсии ω = |k| (звуковые волны). Здесь - скорость звука: . Но мы решим задачу точно и рассмотрим колебания со всеми возможными длинами волн.

Будем искать колебания, зависящие от времени по гармоническому закону: u_n = C_ne^{–iω t} (5).

Здесь ω – частота колебаний, одна и та же для всех атомов (такие колебания называются гармоническими). C_n – комплексная амплитуда колебаний -го атома. Напомним, что колебания описывает вещественная часть уравнения (5), но технически удобно пользоваться комплексным решением.

Такая подстановка – стандартный метод решения линейных систем уравнений с постоянными коэффициентами. В силу линейности уравнений, колебание с произвольной временной зависимостью может быть разложено в интеграл (ряд) Фурье по гармоническим колебаниям.

Из уравнения (2) для амплитуды C_n получаем уравнение:

(6).

Эти уравнения образуют бесконечную систему линейных уравнений. Если применить к цепочке граничные условия Борна-Кармана, то система будет конечной. (Заметим, что условия Борна-Кармана в одномерном случае эквивалентны тому, что цепочка достаточно большой длины L замкнута в кольцо). Тогда, приравняв определитель нулю, можно найти частоты колебаний, а затем, решив систему уравнений для каждой из найденных частот – соответствующие амплитуды.

Но мы поступим иначе. Будем искать решение в виде плоской волны:

(7).

Подставив это выражение в (6), получим:

(8)

Разделим последнее уравнение на exp(ikx_n) и воспользуемся тем, что x_n+1 = x_n+a, x_n–1 = x_n–a: –Mω² = γ(e^ika+e^–ika–2) (9).

Таким образом, подстановка в виде плоской волны оказалась верной: мы избавились от номера атома и получили уравнение, связывающее ω и k, то есть уравнение, определяющее закон дисперсии волн.

Поскольку: (10), то (11).

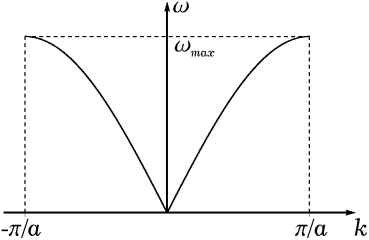
Мы получаем закон дисперсии для упругих колебаний одномерной цепочки: (12).

Итак, мы пришли к выводу, что смещения атомов при колебании одномерной цепочки описываются плоской гармонической волной:

(13).

Точнее, колебания представляют собой произвольную сумму таких волн. Здесь φ – фаза комплексной амплитуды A: A = |A|exp(iφ). Смещение – вещественная величина, которая описывается вещественной частью комплексной плоской гармонической волны, что явно записано в (13). В дальнейшем, при описании вещественных колебаний комплексной плоской волной, будем для краткости опускать обозначение вещественной части.

Волновой вектор k в плоской волне (13) может, вообще говоря, быть любым. Но вследствие дискретности цепочки (x_n может принимать лишь дискретный набор значений na) плоские волны, волновые вектора которых отличаются друг от друга на произвольный вектор обратной решетки 2π l/a, описывают одно и то же колебание. (Здесь l — любое целое число).

Действительно, так как x_n = na, т:

(14).

Поэтому достаточно рассматривать волновые вектора, лежащие в первой зоне Бриллюэна –π/a<k<π/a. Крайние значения волнового вектора ±π/a соответствуют одному и тому же колебанию с минимальной длиной волны λ = 2π/k = 2a. При такой длине волны соседние атомы цепочки движутся в противофазе. Интуитивно ясно, что короче длина волны быть уже не может.

График зависимости ω(k) для одномерной цепочки с одним атомом в примитивной ячейке изображен на рис. 1.2.