Интеграционный метод Эйлера для решения линейных систем алгебраических уравнений
Метод Эйлера для решения линейных систем алгебраических уравнений является итерационным методом, который предполагает задание достаточно близких к искомому решению исходных данных.
В данной работе требуется проанализировать влияние шага на ошибки интегрирования и число итераций, а также сравнить решение обычных и жестких систем. Для этого необходимо составить программу на языке MatLAB, реализующую метод, и протестировать ее при различных исходных данных.
1. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Пусть задана система ОДУ:
![]()
Численное интегрирование этой системы заключается в определении значений x(t) на интервале времени от 0 до Т при заданных начальных условиях х(0). При этом интервал времени от 0 до Т разбивается на шаги с интервалом Dtm=hm=(tm+1-tm), здесь m – номер шага, m=![]() . Очередное значение хm+1 вычисляется на основании предыдущих значений х:
. Очередное значение хm+1 вычисляется на основании предыдущих значений х:
xm+1=xm+hmF(xm,tm)
Для дальнейшего решения системы ОДУ методом Эйлера линеаризируем ее в точке xm,tm:
![]()
Матрица ![]() , при этом
, при этом ![]() суть константы, вычисленные в точке линеаризации:
суть константы, вычисленные в точке линеаризации:
![]() =
=![]()
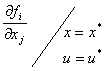
Входной сигнал при линеаризации является известной функцией времени и при фиксированном tm на шаге hm может считаться константой. Элементы матрицы А меняются лишь с изменением точки линеаризации.
Характеристики метода:
1. Точность. Формула xm+1=xm+hmF(xm,tm) аппроксимирует ряд Тейлора для функции x(tm - 1) до линейного по h члена включительно. Поэтому εamiпропорциональна hm2. Можно сказать, что существует такое значение ![]() в интервале
в интервале![]() , при котором
, при котором
ε ![]()
2. Устойчивость. Для анализа устойчивость матрицу А приводят к диагональному виду: A = PλP-1. Тогда система примет вид: x’ = PλP-1x. Нулевое состояние равновесия системы ![]() асимптотически устойчиво при a<0, значит и метод Эйлера для этого уравнения, имеющий вид
асимптотически устойчиво при a<0, значит и метод Эйлера для этого уравнения, имеющий вид![]() , также асимптотически устойчив. При a>0 нулевое состояние равновесия системы неустойчиво. Следовательно, система
, также асимптотически устойчив. При a>0 нулевое состояние равновесия системы неустойчиво. Следовательно, система ![]() также неустойчива.
также неустойчива.
3. Шаг интегрирования. При соблюдении абсолютной или относительной устойчивости:
h<2tmin, ![]()
В любых случаях шаг нужно корректировать по условиям точности.
эйлер линейный уравнение программа интерация
2. ОПИСАНИЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
В этом разделе будут рассмотрены параметры программы и ее логическая структура.
2.1 Общие сведения
Программа написана на языке MatLAB в среде MatLAB 6.5. Для работы программы необходимо наличие операционной системы Windows 95 и выше, а также наличие среды MatLAB 6.5 (на более поздних версиях среды программа не тестировалась). Программа включает в себя 4 файлов: Start.m – головной файл, необходимый для запуска программы на выполнение и построения графика функций и ошибок, Fun.m – содержит ОДУ для вычисления, FunT – функция вычисления точного решения системы, RK1.m – содержит решение системы методом Эйлера.
2.2 Функциональное назначение
Программа предназначена для решения систем линейных ОДУ методом Эйлера. Вывод решения производится по графикам. На них отображены зависимости решения от времени интегрирования.
2.3 Логическая структура
Работу программы можно представить с помощью схемы, изображенной на рис.1:

Рис. 1. Блок-схема программы
Рассмотрим каждый из этапов работы программы подробнее.
Ввод исходных данных осуществляется путем внесения изменений в текст программы.
Далее программа вызывает RK1.m, где происходит решение системы методом Эйлера, следуя алгоритму:
1. задание исходных данных, инициализация переменных
2. вычисление значений х, если выбран способ решения с переменным шагом, то происходит вычисление шага и его сравнение с максимальным, который задан изначально
3. формирование t_out, y_out, в которые заносятся соответственно время интегрирования и значения х.
Далее происходит вызов FunT, где вычисляется точное решение системы.
После чего происходит построение графиков.
2.4 Входные данные
В качестве входных данных выступают:
a) линейное ОДУ
b) шаг интегрирования
c) допустимая ошибка аппроксимации
d) начальные значения х
2.5 Вызов и загрузка
Вызов программы происходит через среду MatLAB. Для этого надо указать директорию доступа к файлам программы и ввести в командную строку имя головного файла – start.m. Программа занимает 1.5 Кб места жесткого диска (начальное время интегрирования). При вычислении результата и построении графиков используется незначительный объем памяти.
2.6 Выходные данные
Выходная информация представляется в графическом виде. Значения всех переменных можно просмотреть через среду MatLAB.
3. ОПИСАНИЕ ТЕСТОВЫХ ЗАДАЧ
В ходе тестирования программ, реализующих метод Эйлера для обычных и жестких линейных ОДУ, исследовалось влияние шага интегрирования на ошибку аппроксимации и число итераций. Для этого исследования вводились различные значения.
3.2 Для обычных линейных ОДУ
Программа тестировалась на системе:
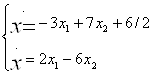
| Величина шага | Ошибка аппроксимации | число итераций |
| 0,1 | 0,0099 | 256 |
| 0,01 | 0,01 | 1932 |
| 0,001 | 0,0073 | 358 |
| 0,0001 | 0,01 | 2569 |
| 0,00001 | 0,0015 | 1 |
При решении этой же системы c переменным шагом число итераций возросло до 2530, при этом ошибка аппроксимации составила 0,0099.
3.3 Для жестких ОДУ
Программа тестировалась на системе:
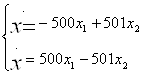
Число итераций при решении системы составило 2016, ошибка аппроксимации равна 0,01.
Величина шага | Ошибка аппроксимации | число итераций |
| 0,1 | 0,0091 | 157 |
| 0,01 | 0,01 | 1169 |
| 0,001 | 0,01 | 7129 |
| 0,0001 | 0,01 | 25258 |
| 0,00001 | 0,0012 | 1 |
В Приложении 2 содержаться графики итераций для шага 0,01 и 0,001 для обычных систем и для шага 0,01 – для жестких.
4. АНАЛИЗ РЕЗУЛЬТАТОВ. ВЫВОДЫ
Проведя анализ результатов тестирования, можно сказать, что наиболее эффективна программа при шаге интегрирования равном 0,00001, так как именно тогда ошибка аппроксимации минимальна и число итераций равно 1.
Видно, что чем меньше ошибка аппроксимации, тем меньше итераций требуется для решения.
При шаге 0,00001 на графики были в виде прямых, что можно списать на округление значений при вычислении.
Исходя из графиков, также можно сказать, что решения совпадают, однако, при заданном максимуме итерационного шага количество итераций в этом методе значительно превышает количество итераций при том же шаге в методе с постоянным шагом, практически не влияя при этом на ошибку аппроксимации.
Проанализировав результаты решения жесткой системы, можно сказать, что плохая обусловленность матрицы делает практически непоказательным графическое решение, так как по нему очень сложно судить о поведении обеих переменных, в силу того что на фоне одной из них (х2) не заметна другая.
То есть:
· величина шага влияет на число итераций
· точность решения зависит от величины шага
· решение систем с переменным или постоянным шагом, равным максимальному шагу способа с переменным шагом, одинаково
· жесткость системы затрудняет анализ результата решения
ЗАКЛЮЧЕНИЕ
В данной работе был исследован явный метод Эйлера для решения обычных и жестких систем ОДУ. Было проанализировано влияние величины шага интегрирования на ошибку аппроксимации, и ее влиянии на число итераций. Для этого была написана программа (Приложение 1), реализующая метод, и протестирована при различных исходных данных.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными.-М.: Мир, 1975.- 558 стр.
2 Самарский А.А., Гулин А.В. Численные методы: Учеб. Пособие для вузов.- М.: Наука,1989.- 432 стр.
3 Сарычева О.М. Численные методы в экономике / О.М. Сарычева.- Новосибирск, 1995.- 67 стр.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
Текст головной программы:
h=0.01; % шаг интегрирования
t0=0; % начальное время интегрирования
x0=(0;0);
Edop=0.01;
(t_out,y_out)=RK1(t0,x0,h,Edop); % вызов RK1
ytoch=FunT(t_out); % точное решение
% построение графика решения методом Рунге-Кутта 1
plot(t_out,y_out);
grid;
title('Solution for x1 and x2 by method Runge-Kutta 1');
ylabel('x');
xlabel('t');
Текст программы для решения ОДУ методом Эйлера с постоянным шагом:
function (t_out,y_out)=RungeKutta1(t0,x0,h,Edop);
% функция решения методом Рунге-Кутта 1
t=t0;
x=x0;
t_out=t;
y_out=x0;
E=(1;1);
while E>Edop
K1=Fun(t,x);
dx=h*K1;
x0=x;
x1=x0+(h/2)*Fun(t+h,x);
x1=x1+(h/2)*Fun(t+h,x1);
x=x+dx;
E=abs(x1-x);
t=t+h;
t_out=(t_out,t);
y_out=(y_out,x);
end
Текст программы для решения ОДУ методом Эйлера с переменным шагом:
function (t_out,y_out)=RungeKutta1(t0,x0,h,Edop);
% функция решения методом Рунге-Кутта 1
t=t0;
hmax=h;
x=x0;
xmax=max(x0)
t_out=t;
y_out=x0;
E=(1;1);
while E>Edop
K1=Fun(t,x);
dx=h*K1;
x0=x;
x1=x0+(h/2)*Fun(t+h,x);
x1=x1+(h/2)*Fun(t+h,x1);
x=x+dx;
E=abs(x1-x);
hi=(0.001*xmax)./(abs(Fun(t,x))+(0.001*xmax)./hmax);
h=min(hi);
if h>hmax
hmax=h;
end
t=t+h;
t_out=(t_out,t);
y_out=(y_out,x);
end
ПРИЛОЖЕНИЕ 2
График функции для явного метода Эйлера для обычной системы ОДУ с постоянным шагом интегрирования 0,01:
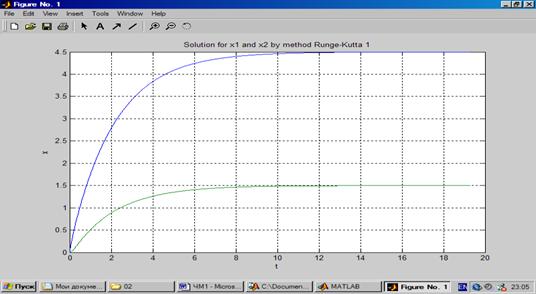
График функции для явного метода Эйлера для обычной системы ОДУ с постоянным шагом интегрирования 0,001:
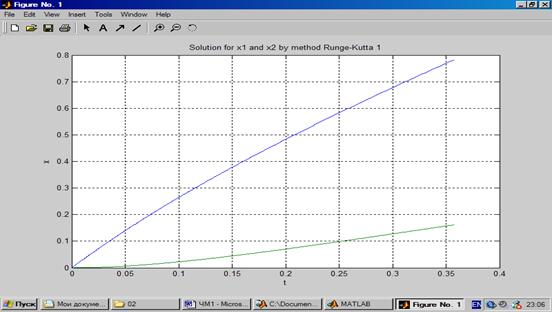
График функции для явного метода Эйлера для обычной системы ОДУ с переменным шагом интегрирования менее 0,01:

График функции для явного метода Эйлера для жесткой системы ОДУ с постоянным шагом интегрирования 0,01:
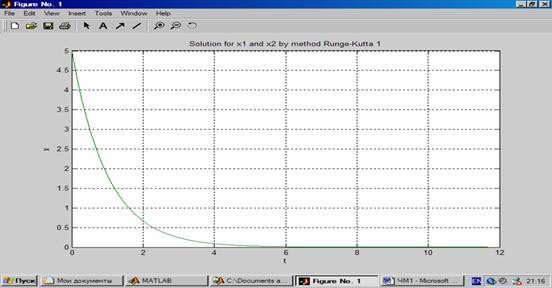
График функции для явного метода Эйлера для жесткой системы ОДУ с постоянным шагом интегрирования 0,001:
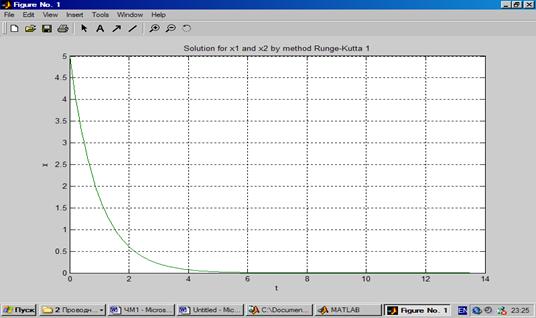
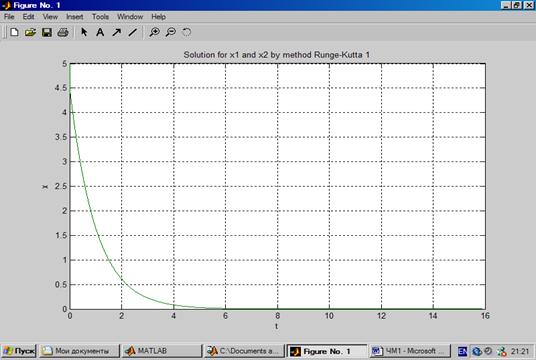
График функции для явного метода Эйлера для жесткой системы ОДУ с переменным шагом интегрирования менее 0,01:
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Интегрирование и дифференцирование интегралов, зависящих от параметра
- Математичні методи представлення знань
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИНаціональний університет “Львівська політехніка”Інститут Комп’ютерних наук та інформаційних т
- Метод квадратных корней для симметричной матрицы при решении систем линейных алгебраических уравнений
- Метод простой итерации для решения систем линейных алгебраических уравнений
В данной курсовой работе необходимо рассмотреть один из множества существующих итерационных методов - метод простой итерации для реше
- Методы поиска экзопланет: метод радиальной скорости, астрометрия, транзитный метод, поляриметрия и др.
Как найти планету вне Солнечной системы? Кажется, что задача изначально кажется невыполнимой, однако на сегодня астрономы достигли зна
- Уравнение Пуассона. Его применение для расчета полей в вакууме
- Теоремы Силова
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

