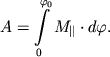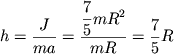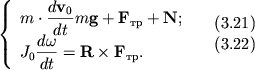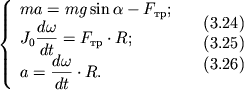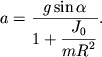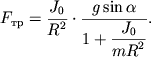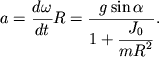Динамика твердого тела
В общем случае абсолютно твердое тело имеет 6 степеней свободы, и для описания его движения необходимы 6 независимых скалярных уравнений или 2 независимых векторных уравнения.
Вспомним, что твердое тело можно рассматривать как систему материальных точек, и, следовательно, к нему применимы те уравнения динамики, которые справедливы для системы точек в целом.
Обратимся к опытам.
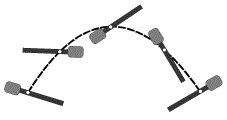
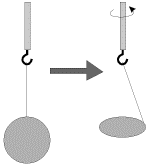
Возьмем резиновую палку, утяжеленную на одном из концов и имеющую лампочку точно в центре масс (рис. 3.1). Зажжем лампочку и бросим палку из одного конца аудитории в другой, сообщив ей произвольное вращение - траекторией лампочки будет при этом парабола - кривая, по которой полетело бы небольшое тело, брошенное под углом к горизонту.
|
Рис. 3.1. |
Стержень, опирающийся одним из концов на гладкую горизонтальную плоскость (рис.1.16), падает таким образом, что его центр масс остается на одной и той же вертикали - нет сил, которые сдвинули бы центр масс стержня в горизонтальном направлении.
Опыт, который был представлен на рис. 2.2 а, в, свидетельствует о том, что для изменения момента импульса тела существенна не просто сила, а ее момент относительно оси вращения.
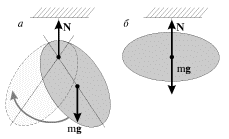
Тело, подвешенное в точке, не совпадающей с его центром масс (физический маятник), начинает колебаться (рис. 3.2а) - есть момент силы тяжести относительно точки подвеса, возвращающий отклоненный маятник в положение равновесия. Но тот же маятник, подвешенный в центре масс, находится в положении безразличного равновесия (рис. 3.2б).
|
Рис. 3.2. |
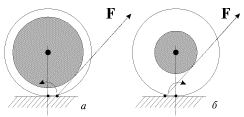
Роль момента силы наглядно проявляется в опытах с "послушной" и "непослушной" катушками (рис. 3.3). Плоское движение этих катушек можно представить как чистое вращение вокруг мгновенной оси, проходящее через точку соприкосновения катушки с плоскостью. В зависимости от направления момента силы F относительно мгновенной оси катушка либо откатывается (рис. 3.За), либо накатывается на нитку (рис. 3.Зб). Держа нить достаточно близко к горизонтальной плоскости, можно принудить к послушанию самую "непослушную" катушку.
|
Рис. 3.3. |
Все эти опыты вполне согласуются с известными законами динамики, сформулированными для системы материальных точек: законом движения центра масс и законом изменения момента импульса системы под действием момента внешних сил. Таким образом, в качестве двух векторных уравнений движения твердого тела можно использовать:
Уравнение движения центра масс
| (3.1) |
Здесь ![]() - скорость центра масс тела,
- скорость центра масс тела, ![]() - сумма всех внешних сил, приложенных к телу.
- сумма всех внешних сил, приложенных к телу.
Уравнение моментов
| (3.2) |
Здесь L- момент импульса твердого тела относительно некоторой точки, ![]() - суммарный момент внешних сил относительно той же самой точки.
- суммарный момент внешних сил относительно той же самой точки.
К уравнениям (3.1) и (3.2), являющимся уравнениями динамики твердого тела, необходимо дать следующие комментарии:
1. Внутренние силы, как и в случае произвольной системы материальных точек, не- влияют на движение центра масс и не могут изменить момент импульса тела.
2. Точку приложения внешней силы можно произвольно перемещать вдоль линии, по которой действует сила. Это следует из того, что в модели абсолютно твердого тела локальные деформации, возникающие в области приложения силы, в расчет не принимаются. Указанный перенос не повлияет и на момент силы относительно какой бы то ни было точки, так как плечо силы при этом не изменится.
Векторы L и M в уравнении (3.2), как правило, рассматриваются относительно некоторой неподвижной в лабораторной системе XYZ точки. Во многих задачах L и M удобно рассматривать относительно движущегося центра масс тела. В этом случае уравнение моментов имеет вид, формально совпадающий с (3.2). В самом деле, момент импульса тела ![]() относительно движущегося центра .масс О связан с моментом импульса
относительно движущегося центра .масс О связан с моментом импульса ![]() относительно неподвижной - точки O' соотношением:
относительно неподвижной - точки O' соотношением:
| (3.3) |
где R - радиус-вектор от O' к О, - полный импульс тела. Аналогичное соотношение легко может быть получено и для моментов силы:
| (3.4) |
где F - геометрическая сумма всех сил, действующих на твердое тело.
Поскольку точка O' неподвижна, то справедливо уравнение моментов (3.2):
| (3.5) |
Тогда
| (3.6) |
Величина ![]() есть скорость точки О в лабораторной системе XYZ. Учитывая (3.4), получим
есть скорость точки О в лабораторной системе XYZ. Учитывая (3.4), получим
| (3.7) |
Поскольку движущаяся точка O - это центр масс тела, то ![]() (
(![]() - масса тела),
- масса тела), ![]() и
и ![]() то есть уравнение моментов относительно движущегося центра масс имеет такой же вид, что и относительно неподвижной точки. Скорости всех точек тела при определении
то есть уравнение моментов относительно движущегося центра масс имеет такой же вид, что и относительно неподвижной точки. Скорости всех точек тела при определении ![]() следует брать относительно центра масс тела.
следует брать относительно центра масс тела.
Ранее было показано, что произвольное движение твердого тела можно разложить на поступательное (вместе с системой x0y0z0, начало которой находится в некоторой точке - полюсе, жестко связанной с телом) и вращательное (вокруг мгновенной оси, проходящей через полюс). С точки зрения кинематики выбор полюса особого значения не имеет, с точки же зрения динамики полюс, как теперь понятно, удобно поместить в центр масс. Именно в этом случае уравнение моментов (3.2) может быть записано относительно центра масс (или оси, проходящей через центр масс) как относительно неподвижного начала (или неподвижное оси).
Если ![]() не зависит от угловой скорости тела, а
не зависит от угловой скорости тела, а ![]() - от скорости центра масс, то уравнения (3.1) и (3.2) можно рассматривать независимо друг от друга. В этом случае уравнение (3.1) соответствует просто задаче из механики точки, а уравнение (3.2) - задаче о вращении твердого тела вокруг неподвижной точки или неподвижной оси. Пример ситуации, когда уравнения (3.1) и (3.2) нельзя рассматривать независимо - движение вращающегося твердого тела в вязкой среде.
- от скорости центра масс, то уравнения (3.1) и (3.2) можно рассматривать независимо друг от друга. В этом случае уравнение (3.1) соответствует просто задаче из механики точки, а уравнение (3.2) - задаче о вращении твердого тела вокруг неподвижной точки или неподвижной оси. Пример ситуации, когда уравнения (3.1) и (3.2) нельзя рассматривать независимо - движение вращающегося твердого тела в вязкой среде.
Далее в этой лекции мы рассмотрим уравнения динамики для трех частных случаев движения твердого тела: вращения вокруг неподвижной оси, плоского движения и, наконец, движения твердого тела, имеющего ось симметрии и закрепленного в центре масс.
I. Вращение твердого тела вокруг неподвижной оси.
В этом случае движение твердого тела определяется уравнением
|
Здесь ![]() - это момент импульса относительно оси вращения, то есть проекция на ось момента импульса, определенного относительно некоторой точки, принадлежащей оси.
- это момент импульса относительно оси вращения, то есть проекция на ось момента импульса, определенного относительно некоторой точки, принадлежащей оси. ![]() - это момент внешних сил относительно оси вращения, то есть проекция на ось результирующего момента внешних сил, определенного относительно некоторой точки, принадлежащей оси, причем выбор этой точки на оси, как и в случае с
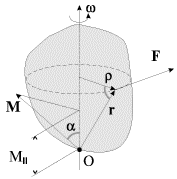
- это момент внешних сил относительно оси вращения, то есть проекция на ось результирующего момента внешних сил, определенного относительно некоторой точки, принадлежащей оси, причем выбор этой точки на оси, как и в случае с ![]() значения не имеет. Действительно (рис. 3.4),
значения не имеет. Действительно (рис. 3.4), ![]() где
где ![]() - составляющая силы, приложенной к твердому телу, перпендикулярная оси вращения,
- составляющая силы, приложенной к твердому телу, перпендикулярная оси вращения, ![]() - плечо силы
- плечо силы ![]() относительно оси.
относительно оси.
|
Рис. 3.4. |
Поскольку ![]() (
(![]() - момент инерции тела относительно оси вращения), то вместо
- момент инерции тела относительно оси вращения), то вместо ![]() можно записать
можно записать
| (3.8) |
или
| (3.9) |
поскольку в случае твердого тела ![]()
Уравнение (3.9) и есть основное уравнение динамики вращательного движения твердого тела вокруг неподвижной оси. Его векторная. форма имеет вид:
| (3.10) |
Вектор ![]() всегда направлен вдоль оси вращения, а
всегда направлен вдоль оси вращения, а ![]() - это составляющая вектора момента силы вдоль оси.
- это составляющая вектора момента силы вдоль оси.
В случае ![]() получаем
получаем ![]() соответственно и момент импульса относительно оси
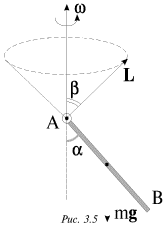
соответственно и момент импульса относительно оси ![]() сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.
сохраняется. При этом сам вектор L, определенный относительно какой-либо точки на оси вращения, может меняться. Пример такого движения показан на рис. 3.5.
|
Рис. 3.5. |
Стержень АВ, шарнирно закрепленный в точке А, вращается по инерции вокруг вертикальной оси таким образом, что угол ![]() между осью и стержнем остается постоянным. Вектор момента импульса L, относительно точки А движется по конический поверхности с углом полураствора
между осью и стержнем остается постоянным. Вектор момента импульса L, относительно точки А движется по конический поверхности с углом полураствора ![]() однако проекция L на вертикальную ось остается постоянной, поскольку момент силы тяжести относительно этой оси равен нулю.
однако проекция L на вертикальную ось остается постоянной, поскольку момент силы тяжести относительно этой оси равен нулю.
Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна).
Скорость i -й частицы тела
| (3.11) |
где ![]() - расстояние частицы до оси вращение Кинетическая энергия
- расстояние частицы до оси вращение Кинетическая энергия
| (3.12) |
так как угловая скорость вращения для всех точек одинакова.
В соответствии с законом изменения механической энергии системы элементарная работа всех внешних сил равна приращению кинетической энергии тела:
| (3.13) |
Работа внешних сил при повороте тела на конечный угол ![]() равна
равна
| (3.14) |
опустим, что диск точила вращается по инерции с угловое скоростью ![]() и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила
и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила ![]() направленная перпендикулярно его оси. Работа этой силы
направленная перпендикулярно его оси. Работа этой силы
|
где ![]() - радиус диска,
- радиус диска, ![]() - угол его поворота. Число оборотов, которое сделает диск до полной остановки,
- угол его поворота. Число оборотов, которое сделает диск до полной остановки,
|
где ![]() - момент инерции диска точила вместе с якорем электромотора.
- момент инерции диска точила вместе с якорем электромотора.
Замечание. Если силы таковы, что ![]() то работу они не производят.
то работу они не производят.
Свободные оси. Устойчивость свободного вращения.
При вращении тела вокруг неподвижной оси эта ось удерживается в неизменном положении подшипниками. При вращении несбалансированных частей механизмов оси (валы) испытывают определенную динамическую нагрузку, Возникают вибрации, тряска, и механизмы могут разрушиться.
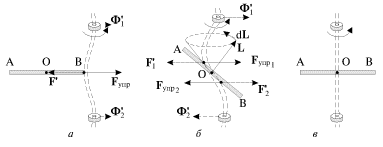
Если твердое тело раскрутить вокруг произвольной оси, жестко связанной с телом, и высвободить ось из подшипников, то ее направление в пространстве, вообще говоря, будет меняться. Для того, чтобы произвольная ось вращения тела сохраняла свое направление неизменным, к ней необходимо приложить определенные силы. Возникающие при этом ситуации показаны на рис. 3.6.
|
Рис. 3.6. |
В качестве вращающегося тела здесь использован массивный однородный стержень АВ, прикрепленный к достаточно эластичной оси (изображена двойными штриховыми линиями). Эластичность оси позволяет визуализировать испытываемые ею динамические нагрузки. Во всех случаях ось вращения вертикальна, жестко связана со стержнем и укреплена в подшипниках; стержень раскручен вокруг этой оси и предоставлен сам себе.
В случае, изображенном на рис. 3.6а, ось вращения является для точки В стержня главной, но не центральной, ![]() Ось изгибается, со стороны оси на стержень действует сила
Ось изгибается, со стороны оси на стержень действует сила ![]() обеспечивающая его вращение (в НИСО, связанной со стержнем, эта сила уравновешивает центробежную силу инерции). Со стороны стержня на ось действует сила
обеспечивающая его вращение (в НИСО, связанной со стержнем, эта сила уравновешивает центробежную силу инерции). Со стороны стержня на ось действует сила ![]() уравновешенная силами
уравновешенная силами ![]() со стороны подшипников.
со стороны подшипников.
В случае рис. 3.6б ось вращения проходит через центр масс стержня и является для него центральной, но не главной. Момент импульса относительно центра масс О не сохраняется и описывает коническую поверхность. Ось сложным образом деформируется (изламывается), со стороны оси на стержень действуют силы ![]() и
и ![]() момент которых обеспечивает приращение
момент которых обеспечивает приращение ![]() (В НИСО, связанной со стержнем, момент упругих сил компенсирует момент центробежных сил инерции, действующих на одну и другую половины стержня). Со стороны стержня на ось действуют силы
(В НИСО, связанной со стержнем, момент упругих сил компенсирует момент центробежных сил инерции, действующих на одну и другую половины стержня). Со стороны стержня на ось действуют силы ![]() и
и ![]() направленные противоположно силам
направленные противоположно силам ![]() и
и ![]() Момент сил
Момент сил ![]() и
и ![]() уравновешен моментом сил
уравновешен моментом сил ![]() и
и ![]() возникающих в подшипниках.
возникающих в подшипниках.
И только в том случае, когда ось вращения совпадает с главной центральной осью инерции тела (рис.3.6в), раскрученный и предоставленный сам себе стержень не оказывает на подшипники никакого воздействия. Такие оси называют свободными осями, потому что, если убрать подшипники, они будут сохранять свое направление в пространстве неизменным.
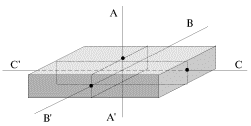
Иное дело, будет ли это вращение устойчивым по отношению к малым возмущениям, всегда имеющим место в реальных условиях. Опыты показывают, что вращение вокруг главных центральных осей с наибольшим и наименьшим моментами инерции является устойчивым, а вращение вокруг оси с промежуточным значением момента инерции - неустойчивым. В этом можно убедиться, подбрасывая вверх тело в виде параллелепипеда, раскрученное вокруг одной из трех взаимно перпендикулярных главных центральных осей (рис. 3.7). Ось AA' соответствует наибольшему, ось BB' - среднему, а ось CC' - наименьшему моменту инерции параллелепипеда. Если подбросить такое тело, сообщив ему быстрое вращение вокруг оси AA' или вокруг оси CC', можно убедиться в том, что это вращение является вполне устойчивым. Попытки заставить тело вращаться вокруг оси BB' к успеху не приводят - тело движется сложным образом, кувыркаясь в полете.
|
Рис. 3.7. |
В телах вращения устойчивой оказывается свободная ось, соответствующая наибольшему моменту инерции. Так, если сплошной однородный диск подвесить к быстровращающемуся валу электромотора (рис. 3.8, ось вращения вертикальна), то диск довольно быстро займет горизонтальное положение, устойчиво вращаясь вокруг центральной оси, перпендикулярной к плоскости диска.
|
Рис. 3.8. |
Центр удара.
Опыт показывает, что если тело, закрепленное на оси вращения, испытывает удар, то действие удара в общем случае передается и на ось. При этом величина и направление силы, приложенной к оси, зависят от того, в какую точку тела нанесен удар.
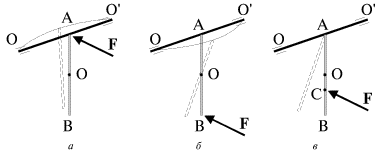
Рассмотрим сплошной однородный стержень АВ, подвешенный в точке А на горизонтальной, закрепленной в подшипниках оси OO' (рис. 3.9). Если удар (короткодействующая сила F ( нанесен близко к оси вращения, то ось прогибается в направлении действия силы F (рис. 3.9а). Если удар нанесен по нижнему концу стержня, вблизи точки В, то ось прогибается в противоположном направлении (рис. 3.9б). Наконец, если удар нанесен в строго определенную точку стержня, называемую центром удара (рис. 3.9в, точка С), то ось не испытывает никаких дополнительных нагрузок, связанных с ударом. Очевидно, в этом случае скорость поступательного движения, приобретаемого точной А вместе с центром масс O, будет компенсироваться линейной скоростью вращательного движения вокруг центра масс О (оба эти движения инициируются силой F и происходят одновременно).
|
Рис. 3.9. |
Вычислим, на каком расстоянии ![]() от точки подвеса стержня находится центр удара. Уравнение моментов относительно оси вращения OO' дает
от точки подвеса стержня находится центр удара. Уравнение моментов относительно оси вращения OO' дает
| (3.15) |
Сил реакции со стороны оси, как предполагается, при ударе не возникает, поэтому на основании теоремы о движении центра масс можно записать
| (3.16) |
где ![]() - масса тела,
- масса тела, ![]() - скорость центра масс. Если
- скорость центра масс. Если ![]() - расстояние от оси до центра масс тела, то
- расстояние от оси до центра масс тела, то
| (3.17) |
и в результате из уравнения моментов и уравнения движения центра масс находим
| (3.18) |
При этом точка C (центр удара) совпадает с так называемым центром качания данного физического маятника - точкой, где надо сосредоточить всю массу твердого тела, чтобы полученный математический маятник имел такой же период колебаний, как и данный физический.
В случае сплошного однородного стержня длиной ![]() имеем:
имеем:
|
Замечание. Полученное выражение для ![]() (3.18) справедливо и для произвольного твердого тела. При этом надо только иметь в виду, что точка подвеса тела А и центр масс О должны лежать на одной вертикали, а ось вращения должна совпадать с одной из главных осей инерции тела, проходящих через точку А.
(3.18) справедливо и для произвольного твердого тела. При этом надо только иметь в виду, что точка подвеса тела А и центр масс О должны лежать на одной вертикали, а ось вращения должна совпадать с одной из главных осей инерции тела, проходящих через точку А.
Пример 1. При ударах палкой длиной ![]() по препятствию рука "не чувствует" удара (не испытывает отдачи) в том случае, если удар приходится в точку, расположенную на расстоянии
по препятствию рука "не чувствует" удара (не испытывает отдачи) в том случае, если удар приходится в точку, расположенную на расстоянии ![]() свободного конца палки.
свободного конца палки.
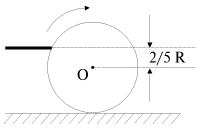
Пример 2. При горизонтальном ударе кием по бильярдному шару (рис. 3.10) шар начинает качение без проскальзывания в том случае, еcли удар нанесен в точку, находящуюся на высоте
|
от поверхности бильярда, то есть на ![]() выше центра шара. Если удар будет нанесен ниже, качение будет сопровождаться скольжением в направлении движении шара. Если удар нанесен выше, то шар в точке касания с бильярдным столом будет проскальзывать назад.
выше центра шара. Если удар будет нанесен ниже, качение будет сопровождаться скольжением в направлении движении шара. Если удар нанесен выше, то шар в точке касания с бильярдным столом будет проскальзывать назад.
|
Рис. 3.10. |
Рассмотренные примеры формально не относятся к вращению твердого тела вокруг неподвижной оси, однако все приведенные выше соображения о центре удара, очевидно, остаются в силе и в этих случаях.
II. Плоское движение твердого тела.
Напомним, что при плоском движении все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости, поэтому достаточно рассмотреть движение одного из сечения тела, например, того, в котором лежит центр масс. При разложении плоского движения на поступательное и вращательное скорость поступательного движения определена неоднозначно - она зависит от выбора оси вращения, однако угловая скорость вращательного движения оказывается одной и той же.
Если в качестве оси вращения выбрать ось, проходящую через центр масс, то уравнениями движения твердого тела будут:
1. Уравнение движения центра масс
| (3.19) |
2. Уравнение моментов относительно оси, проходящей через центр масс
| (3.20) |
Особенностью плоского движения является то, что ось вращения сохраняет свою ориентацию в пространстве и остается перпендикулярной плоскости, в которой движется центр масс. Еще раз подчеркнем, что уравнение моментов (3.20) записано относительно, в общем случае, ускоренно движущегося центра масс, однако, как было отмечено в начале лекции, оно имеет такой же вид, как и уравнение моментов относительно неподвижной точки.
В качестве примера рассмотрим задачу о скатывании цилиндра с наклонное плоскости. Приведем два способа решения этой задачи с использованием уравнений динамики твердого тела.
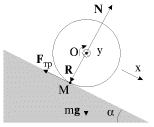
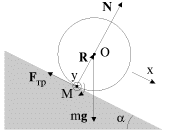
Первый способ. Рассматривается вращение цилиндра относительно оси, проходящее через центр масс (рис. 3.11).
|
Рис. 3.11. |
Система уравнений (3.19 - 3.20) имеет вид:
|
К этой системе необходимо добавить уравнение кинематической связи
| (3.23) |
Последнее уравнение получается из условия, что цилиндр скатывается без проскальзывания, то есть скорость точки М цилиндра равна нулю.
Уравнение движения центра масс (3.1) запишем для проекций ускорения и сил на ось x вдоль наклонной плоскости, а уравнение моментов (3.22) - для проекций углового ускорения и момента силы трения на ось y , совпадающую с осью цилиндра. Направления осей x и у выбраны согласованно, в том смысле, что положительному линейному ускорению оси цилиндра соответствует положительное же угловое ускорение вращения вокруг этой оси. В итоге получим:
|
откуда
| (3.27) |
Следует подчеркнуть, что ![]() - сила трения сцепления - может принимать любое значение в интервале от О до
- сила трения сцепления - может принимать любое значение в интервале от О до ![]() (сила трения скольжения) в зависимости от параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное вращение цилиндра при его скатывании с наклонной плоскости. В данном случае
(сила трения скольжения) в зависимости от параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное вращение цилиндра при его скатывании с наклонной плоскости. В данном случае
| (3.28) |
Если цилиндр сплошной, то
| (3.29) |
Качение без проскальзывания определяется условием
| (3.30) |
где ![]() - коэффициент трения скольжения,
- коэффициент трения скольжения, ![]() - сила реакции опоры. Это условие сводится к следующему:
- сила реакции опоры. Это условие сводится к следующему:
| (3.31) |
или
| (3.32) |
Второй способ. Рассматривается вращение цилиндра относительно неподвижной оси, совпадающей в данный момент времени с мгновенной осью вращения (рис. 3.12).
|
Рис. 3.12. |
Мгновенная ось вращения проходит через точку соприкосновения цилиндра и плоскости (точку М). При таком подходе отпадает необходимость в уравнении движении центра масс и уравнении кинематической связи. Уравнение моментов относительно мгновенной оси имеет вид:
| (3.33) |
Здесь
| (3.34) |
В проекции на ось вращения (ось y)
| (3.35) |
Ускорение центра масс выражается через угловое ускорение
| (3.36) |
Кинетическая энергия при плоском движении.
Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:
| (3.37) |
где ![]() - скорость центра масс тела,
- скорость центра масс тела, ![]() - скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
- скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:
| (3.38) |
так как ![]() (суммарный импульс частиц в системе центра масс равен нулю).
(суммарный импульс частиц в системе центра масс равен нулю).
Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.
В этой связи задачу о скатывании цилиндра с наклонной плоскости можно решить, используя закон сохранения механической энергии (напомним, что сила трения при качении без проскальзывания работу не совершает).
Приращение кинетической энергии цилиндра равно убыли его потенциальное энергии:
| (3.39) |
Здесь ![]() - длина наклонной плоскости,
- длина наклонной плоскости, ![]() - момент инерции цилиндра относительно мгновенной оси вращения.
- момент инерции цилиндра относительно мгновенной оси вращения.
Поскольку скорость оси цилиндра ![]() то
то
| (3.40) |
Дифференцируя обе части этого уравнения по времени, получим
| (3.41) |
откуда для линейного ускорения![]() оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).
оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).
Замечание. Если цилиндр катится с проскальзыванием, то изменение его кинетической энергии будет определяться также и работой сил трения. Последняя, в отличие от случая, когда тело скользит по шероховатой поверхности, не вращаясь, определяется, в соответствии с (3.14), полным углом поворота цилиндра, а не расстоянием, на которое переместилась его ось.
Динамика твердого тела на данном этапе используется для тел, движущихся в сплошной среде.
В задаче о полете тела с тремя несущими поверхностями при наличии динамической асимметрии определены условия, при которых проявляются синхронизмы 1:3. С увеличением угловой скорости вращения тела около продольной оси даже на поверхности рассеивания заметно ослабление этого эффекта.
Разработана программа имитационного моделирования комплекса задач по динамике полета противоградовых ракет. С ее помощью построены таблицы введения поправок на установочные углы запуска ракет для наилучшей компенсации вредного влияния ветра.
Создана механико-математическая модель полета бумеранга. Открыта лаборатория навигации и управления.
Разработан и внедрен на аэродинамической трубе А-8 комплекс механического оборудования и сопутствующей измерительной аппаратуры для проведения динамических испытаний моделей. Определены коэффициенты демпфирования поперечных колебаний осесимметричных оперенных тел различного удлинения при раскрутке вокруг собственной оси
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Дисперсия света
- Дифференциальные уравнения движения точки. Решение задач динамики точки
Министерство Общего и профессионального технического образованияМосковский Государственный Технический Университет МАМИ Кафедра: Те
- Дослідження впливу наповнювача на структурну організацію і міжфазну взаємодію в композиційних полімерних матеріалах
- Дуговой разряд в газах
- Жан Батист Жозеф Фурье
Жан Батист Жозеф Фурье.(21.3.1768-16.5.1830) Французский математик,член Парижской АН (1817). Окончив военную школу в Осере, где родился, работал там ж
- Железные Дороги России
Системы электроснабжения электрифицированных железных дорог по предъявляемым к ним требованиям, условиям работы, используемому обору
- Жизнь и деятельность А С Попова
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.