Дуговой разряд в газах
План:
ВВедение.
Свойства дугового разряда.
1.Образование дуги.
2. Катодное пятно. Внешний вид и отдельные части
дугового разряда.
3. Распределение потенциала и вольтамперная
характеристика при дуговом разряде.
4. Температура и излучение отдельных частей дугового разряда.
5. Генерация незатухающих колебаний при помощи элек-
трической дуги.
6. Положительный столб дугового разряда при высоком
и сверхвысоком давлении.
III. Применение дугового разряда.
1. Современные методы электрообработки.
2. Электродуговая сварка.
3.Плазменная технология.
4.Плазменная сварка.
IV. Заключение.
I
Дуговой разряд в виде так называемой электрической (или вольтовой) дуги был впервые обнаружен в 1802 году русским учёным профессором физики Военно-медико-хирургической академии в Петербурге, а впоследствии академиком Петербургской Академии наук Василием Владимировичем Петровым. Петров следующими словами описывает в одной из изданных им книг свои первые наблюдения над электрической дугой:
«Если на стеклянную плитку или на скамеечку со стеклянными ножками будут положены два или три древесных угля... и если металлическими изолированными направлятелями...сообщенными с обоими полюсами огромной батареи, приближать оные один к другому на расстояние от одной до трёх линий,то является между ними весьма яркий белого цвета свет или пламя, от которого оные угли скорее или медлительнее загораются и от которого тёмный покой довольно ясно освещен быть может... ».
Путь к электрической дуге начался в глубокой древности. Еще греку Фалесу Милетскому, жившему в шестом веке до нашей эры, было известно свойство янтаря притягивать при натирании легкие предметы—перышки, солому, волосы и даже создавать искорки. Вплоть до семнадцатого века это был единственный способ электризации тел, не имевший никакого практического применения. Ученые искали объяснение этому явлению.
Английский физик Уильям Гильберт (1544—1603) установил, что и другие тела (например, горный хрусталь, стекло), подобно янтарю, обладают свойством притягивать легкие предметы после натирания. Он назвал эти свойства электрическими, впервые введя этот термин в употребление (по-гречески янтарь—электрон).
Бургомистр из Магдебурга Отто фон Герике (1602—1686) сконструировал одну из первых электрических машин. Это была электростатическая машина, представлявшая собой серный шар, укрепленный на оси. Одним из полюсов служил... сам изобретатель. При вращении рукоятки из ладоней довольного бургомистра с легким потрескиванием вылетали синеватые искры. Позднее машину Герике усовершенствовали другие изобретатели. Серный шар был заменен стеклянным, а вместо ладоней исследователя в качестве одного из полюсов приме- нены кожаные подушечки.
Большое значение имело изобретение в восемнадцатом веке лейденской банки—конденсатора, позволившего накапливать электричество. Это был стеклянный сосуд с водой, обернутый фольгой. В воду погружали металлический стержень, пропущенный через пробку.
Американский ученый Бенджамин Франклин (1706—1790) доказал, что вода в собирании электрических зарядов никакой роли не играет, этим свойством обладает стекло—диэлектрик.
Электростатические машины получили довольно широкое распространение, но лишь как забавные вещицы. Были, правда, попытки лечения больных с помощью электричества, однако каков был физиотерапевтический эффект такого лечения, сказать трудно.
Французский физик Шарль Кулон (1736—1806)— основатель электростатики-в 1785 г. установил, что сила взаимодействия электрических зарядов пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними.
В сороковых годах восемнадцатого века Бенджамин Франклин выдвинул теорию о том, что существует электричество только одного рода—особая электрическая материя, состоящая из мельчайших частиц, способных проникать внутрь вещества. Если в теле имеется избыток электрической материи, оно заряжено положительно, при ее недостатке—тело заряжено отрицательно. Франклин ввел в практику знаки «плюс» и «минус»,а также термины: конденсатор, проводник, заряд.
С оригинальными теориями о природе электричества выступили М. В. Ломоносов (1711—1765), Леонард Эйлер (1707—1783), Франц Эпинус (1724—1802) и другие ученые. К концу восемнадцатого века свойства и поведение неподвижных зарядов были достаточно изучены и в какой-то мере объяснены. Однако ничего не было известно об электрическом токе—движущихся зарядах, так как не существовало устройства, которое могло бы заставить двигаться большое количество зарядов. Токи, получаемые от электростатической машины,были слишком малы, их нельзя было измерить.
II
1. Если в тлеющем разряде увеличивать силу тока, уменьшая внешнее сопротивление, то при большой силе тока напряжение на зажимах трубки начинает падать, разряд быстро развива-ется и превращается в дуговой. В большинстве случаев переход совершается скачком и практически нередко ведёт к короткому замыканию. При подборе сопротивления внешнего контура удаётся стабилизовать переходную форму разряда и наблюдать при определённых давлениях непрерывный переход тлеющего разряда в дугу. Параллельно с падением напряжения между электродами трубки идёт возрастание температуры катода и постепенное уменьшение катодного падения.
Применение обычного способа зажигания дуги путём раздвигания электродов вызвано тем, что дуга горит при сравнительно низких напряжениях в десятки вольт, тогда как для зажигания тлеющего разряда нужно при атмосферном давлении напряжение порядка десятков киловольт. Процесс зажигания при раздвигании электродов объясняется местным нагреванием электродов вследствие образования между ними плохого контакта в момент разрыва цепи.
Вопрос о развитии дуги при разрыве цепи технически важен не только с точки зрения получения «полезных» дуг, но также и с точки зрения борьбы с «вредными» дугами, например с образованием дуги при размыкании рубильника. Пусть L-само- индукция контура, W—его сопротивление, ع—э.д.с. источника тока,U(I)—функция вольтамперной характеристики дуги. Тогда мы должны иметь: ع= L dI/dt+WI+U(I) (1) или
LdI/dt=(ع-WI)-U(I)=∆ (2).
Разность (ع — WI) есть не что иное, как ордината прямой сопротивления АВ (рис.1), а U(I)— ордината характеристики дуги при данном I. Чтобы dI/dt было отрицательно, т.е.Чтобы ток I непременно уменьшался со временем и между электродами рубильника не образовалось стойкой дуги, надо, чтобы
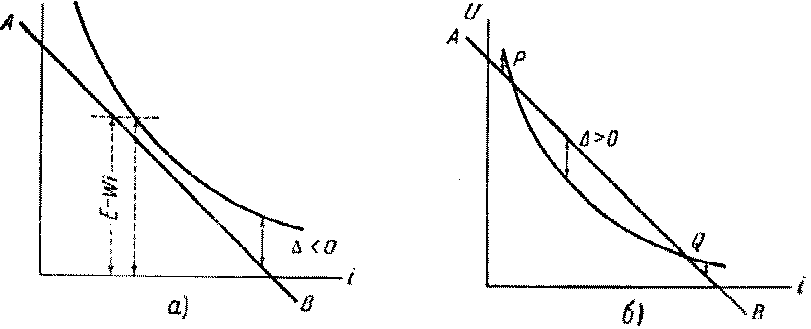
Рис.1. Относительное положение прямой сопротивления и кривой вольтамперной характеристики установившейся дуги для случаев:а)когда дуга пе может возникнуть при разрыве цепи; б)когда дуга возникает при разрыве в интервале силы тока, соответствующем точкам Р и Q.
имело место ∆<0, т. е. надо, чтобы во всех точках харак-теристики соблюдалось неравенство U(I)>ع-WI.
Для этого характеристика всеми своими точками должна лежать выше прямой сопротивления (рис. 1, а). Это простое заклю-чение пе учитывает ёмкости в цепи и относится лишь к постоянному току.
Точка пересечения прямой сопротивления с кривой вольт-амперной характеристики установившейся дуги соответствует низшему пределу силы постоянного тока, при котором может возникнуть дуга при разрыве цепи (рис. 1, б). В случае размыкания рубильником дуги переменного тока,потухающей при каждом переходе напряжения через нуль, существенно, чтобы условия,имеющиеся налицо в разрядном промежутке при размы-кании, не допускали нового зажигания дуги при последующем возрастании напряжения источника тока. Для этого требует-ся,чтобы при возрастании напряжения разрядный промежуток был достаточно деионизован. В выключателях сильных перемен-ных токов искусственно добиваются усиленной деионизации путём введения специальных электродов, отсасывающих заря-женные частицы газа благодаря двуполярной диффузии, а также путём применения механического дутья или путём воздействия на разряд магнитным полем. При высоких напряжениях при-меняют масляные выключатели.
2. Катодное пятно, неподвижное на угольном катоде, на поверхности жидкой ртути находится в непрерывном быстром движении. Положение катодного пятна на поверхности жидкой ртути может быть закреплено при помощи металлического штифта, погруженного в ртуть и немного высовывающегося из неё.
В случае небольшого расстояния между анодом и катодом тепловое излучение анода сильно влияет на свойства катод-ного пятна. При достаточно большом расстоянии анода от угольного катода размеры катодного пятна стремятся к неко-торому постоянному предельному значению, и площадь, занима-емая катодным пятном на угольном электроде в воздухе, пропорциональна силе тока и соответствует при атмосферном давлении 470 а/смІ.Для ртутной дуги в вакууме найдено 4000 а/смІ.
При уменьшении давления площадь, занимаемая катодным пятном на угольном катоде, при постоянной силе тока увели-чивается.
Резкость видимой границы катодного пятна объясняется тем, что сравнительно медленному уменьшению температуры с удале-нием от центра пятна соответствует быстрое падение как све-тового излучения, так и термоэлектронной эмиссии, а это равносильно резкой «оптической» и «электрической» границам пятна.
Угольный катод при горении дуги в воздухе заостряется, тогда как на угольном аноде, если разряд не перекрывает всю переднюю площадь анода, образуется круглое углубление—положительный кратер дуги.
Образованно катодного пятна объясняется следующим образом. Распределение пространственных зарядов в тонком слое у катода таково, что здесь разряд требует для своего поддержания тем меньшей разницы потенциалов, чем меньше поперечное сечение канала разряда. Поэтому разряд на катоде должен стягиваться.
Непосредственно к катодному пятну прилегает часть разряда, называемая отрицательной пли катодной кистью или отрицательным пламенем. Длина катодной кисти в дуге при низком давлении определяется тем расстоянием, на которое залетают быстрые первичные электроны, получившие свои ско-рости в области катодного падения потенциала.
Между отрицательной кистью и положительным столбом расположена область, аналогичная фарадееву тёмному пространству тлеющего разряда. В дуге Петрова в воздухе, кроме отрицательной кисти, имеется положи-тельное пламя и ряд ореолов. Спектральный анализ указывает на наличие в этих пламенах и ореолах ряда химических соединений (циана и окислов азота).
При горизонтальном расположении электродов и большом давлении газа положительный столб дугового разряда изги-бается кверху под действием конвекционных токов нагретого разрядом газа. Отсюда произошло самое название дуговой разряд.
3. В дуге Петрова высокая температура и высокое давление не дают возможности использовать для измерения распреде-ления потенциала метод зондов.
Падение потенциала между электродами дуги складывается из катодного падения и Uк, анодного падения Uа и падения в положительном столбе. Сумму катодного и анодного падений потенциала можно определить,сближая анод и катод до исчез-новения положительного столба и измеряя напряжение между электродами.В случае дуги при низком давлении можно опре-делить значения потенциала в двух точках столба дуги, поль-зуясь методом зондовых характеристик, вычислить отсюда продольный градиент потенциала и далее подсчитать как анодное, так и катодное падение потенциала.
Установлено, что в дуговом рязряде при атмосферном давлении сумма катодного и анодного падений примерно той же величины,что и ионизационный потенциал газа или пара, в котором происходит разряд.
В технике применения дуги Петрова с угольными электродами обычно пользуются эмпирической формулой Айртона:
U=a+bl+(c+dl)/I (3)
Здесь U—напряжение между электродами, I—сила тока в дуге, l—длина дуги, а, b, с и d—четыре постоянных. Формула характеристики (3) установлена для дуги между угольными электродами в воздухе. Под l подразумевается расстояние между катодом и плоскостью, проведённой через края положи-тельного кратера.
Перепишем формулу (4) в виде
U=а+c/I+l(b+d/I). (4)
В (4) члены, содержащие множитель l, соответствуют падению потенциала в положительном столбе; первые два члена представляют собой сумму катодного и ано-дного падения Uк+Uа. Постоянные в (3) зависят от давления воздуха и от условий охлаждения электродов, а следовательно, от размеров и формы углей.
В случае дугового разряда в откачанном сосуде, запол-ненном парами металла (например, ртути), давление пара зависит от температуры наиболее холодных частей сосуда и поэтому ход характеристики сильно зависит от условий охлаждения всей трубки.
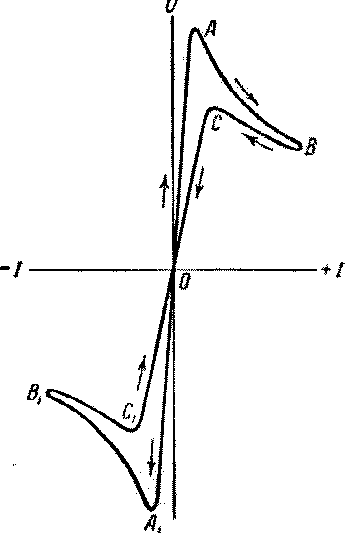
Динамическая характеристика дугового разряда силь-но отличается от статической. Вид динамической характеристики зависит от быстроты изменения режима дуги. Практически наиболее интересна характеристика дуги при питании переменным током. Одновременное осциллографирование тока и напряжения даёт картину, изображенную на рис.2. Начерченная по этим кривым характеристика дуги за целый период имеет
вид, представленный на рис.3. Пунктиром покыазан ход напряжения при отсутствии разряда.
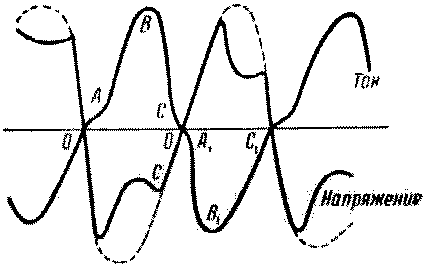
Р
Рис.4. Динамическая характерис-
тика дугового разряда на
переменном токе низкой частоты.
ис. 3. Осциллограмма тока и напряжения дугового разряда на переменном токенизкой частоты. Точки А, В, С и т.д.
соответствуют точкам,обозначенным теми
же буквами на рис.4.
Катод, не успевший ещё охладиться после разряда, имевшего место в предыдущем полупериоде тока, с самого начала полупериода, когда внешняя э.д.с. проходит через нуль, эмиттирует электроны. От точки О до точки А характеристика соответствует несамостоятельному разряду, источником которого являются эмиттируемые катодом электроны. В точке А происходит зажигание дуги. После точки А разрядный ток быстро увеличивается. При наличии сопротивления во внешней цепи напряжение между электродами дуги падает, хотя э.д.с. источника тока (пунктир на рис.3), пробегая синусоиду, ещё увеличивается. С уменьшением напряжения и тока, даваемого внешним источником, разрядный ток начинает уменьшаться.
С уменьшением тока в дуге напряжение между её электро-дами может вновь возрасти в зависимости от внешнего сопро-тивления, но часть ВС характеристики на рис.4 может быть и горизонтальной или иметь про-тивоположный наклон. В точке С имеет место потухание дуги.
После точки С ток несамостоятельного разряда уменьшается до нуля вместе с уменьшением напряжения между электродами.
П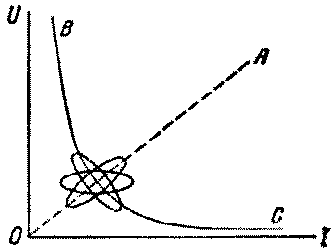
осле перехода напряжения через
нуль роль катода начинает играть прежний анод и картина повторяется при обратных знаках тока и напряжения.
Рис.5. Изменение динамической харак-теристики при повышенной частоты переменного тока, наложенного на пос-тоянный.
На вид динамической харак-теристики оказывают влияние все условия, определяющие режим дуги: расстояние между элек-тродами, величина внешнего сопро-тивления, самоиндукция и ёмкость внешней цепи, частота переменного тока, питающего дугу, и т. д.
Если на электроды дуги, питаемой постоянным током, на-ложить переменное напряжение амплитуды, меньшей, чем напряжение питающего дугу постоянного тока, то харак-теристика имеет вид замкнутой петли, охватывающей стати-ческую характеристику ВС с двух сторон. При увеличении частоты переменного тока ось этой петли поворачивается, сама петля сплющивается и, наконец, стремится принять вид отрезка прямой ОА, проходящей через начало координат (рис.5). При очень малой частоте петля динамической харак-теристики превращается в отрезок статической характеристики ВС, так как все внутренние параметры разряда,в частности концентрация ионов и электронов, успевают в каждой точке характеристики принимать значения, соответствующие стацио-нарному разряду при данных U и I. Наоборот, при очень быстром изменении и параметры разряда совершенно не успе-вают изменяться, поэтому I оказывается пропорциональным и, что соответствует прямой ОА, проходящей через начало координат.Таким образом, при увеличении частоты переменного тока петля характеристики (рис. 5) становится во всех своих точках возрастающей.
В связи с возможностью полной ионизации газа в дуговом
разряде стоит вопрос об обрыве дуги при малом давлении газа
и очень сильных токах. В явлении обрыва дуги существенную роль играет значительное уменьшение плотности газа вслед-ствие электрофореза и отсоса ионов к стенкам, особенно в таких местах, где разрядный промежуток сильно сужен. Прак-тически это приводит к необходимости избегать чрезмерных сужений при постройке ртутных выпрямителей на очень большие силы тока.
Электрики, имевшие впервые дело с электрической дугой,
пытались применить закон Ома также и в этом случае. Для получения результатов расчёта по закону Ома, согласных с действительностью, им пришлось ввести представление об обратной электродвижущей силе дуги. По аналогии с явлениями в гальванических элементах, предполагаемое появление этой э.д.с. назвали поляризацией дуги. Вопросу об обратной э.д.с. дуги посвящены работы русских учёных Д. А. Лачинова и В. Ф. Миткевича. Дальнейшее развитие представлений об электрических разрядах в газах показало, что такая пос-тановка вопроса является чисто формальной и может быть с успехом заменена представлением о падающей характеристике дуги. Справедливость этой точки зрения подтверждается неу-дачей всех попыток непосредственно обнаружить эксперимен-тально обратную э.д.с. электрической дуги.
4. В случае дуги в воздухе между угольными электродами
преобладает излучение раскалённых электродов, главным образом,положительного кратера.
Излучение анода, как излучение твёрдого тела, обладает
сплошным спектром. Интенсивность его определяется темпера-турой анода. Послздняя является характерной величиной для дуги в атмосферном воздухе при аноде из какого-либо данного материала, так как температура анода от силы тока не зави-сит и определяется исключительно температурой плавления или иозгонки материала анода. Температура плавления или возгон-ки зависит от давления, под которым находится плавящееся или возгоняемое тело. Поэтому температура анода, а следова-тельно, и интенсивность излучения положительного кратера зависят от давления, при котором горит дуга. В этом отно-шении известны классические опыты с угольной дугой под давленрюм, приведшие к получению очень высоких температур.
Об изменении температуры положительного кратера с давле-
нием даёт понятие кривая рис. 6. Прямая линия, на которую
на этом чертеже укладываются точки для давлений от 1 атм
и выше, служит подтверждением предположения, что темпера-тура положительного кратера определяется температурой плав-ления или возгонки вещества анода, так как в этом случае должна существовать линейная зависимость между ln р и 1/T. Отступление от линейной зависимости при более низких дав-лениях объясняется тем, что при давлении ниже 1 атм коли-чество тепла, выделяющееся на аноде, недостаточно для н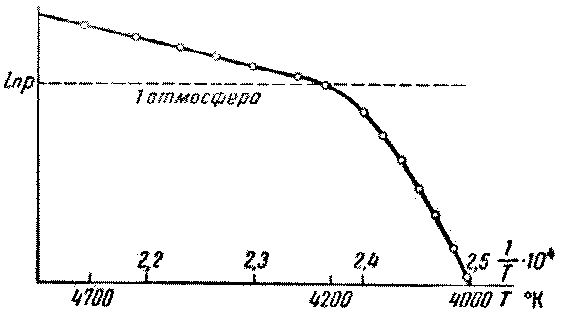
Рис. 6. Изменение температуры угольного анода электрической дкги в воздухе при изменении давления. Шкала по оси ординат логарифмическая.
агревания анода до температуры плавления или возгонки.
Температура катодного пятна дуги Петрова всегда на несколь-
ко сот градусов ниже температуры положительного кратера.
Высокие температуры шнура дуги не могут быть определены
при помощи термоэлемента или болометра. В настоящее время
для определения температуры в дуге применяют спектральные
методы.
При больших силах тока температура газа в дуге Петрова
может быть выше температуры анода и достигает 6000° К. Такие высокие температуры газа характерны для всех случаев дугового разряда при атмосферном давлении. В случае очень больших давлений (десятки и сотни атмосфер) температура в центральных частях отшнуровавшегося положительного столба дуги доходит до 10 000° К. В дуговом разряде при низких давлениях температура газа в положительном столбе того же порядка, как и в положительном столбе тлеющего разряда.
Температура положительного кратера дуги выше, чем темпе-ратура катода, потому что на аноде весь ток переносится электронами, бомбардирующими и нагревающими анод. Электроны
отдают аноду не только всю приобретённую в области анодного
падения кинетическую энергию, но ещё и работу выхода(«скры-
тую теплоту испарения» электронов). Напротив, на катод по-
падает и его бомбардирует и нагревает малое число положи-тельных ионов по сравнению с числом электронов, попадающих на анод при той же силе тока. Остальная часть тока на като-де осуществляется электронами, при выходе которых в случае
термоэлектронной дуги на работу выхода затрачивается тепло-
вая энергия катода.
5. Благодаря тому, что дуга имеет падающую характеристику, она может быть использована в качестве генератора незатуха-ющих колебаний. Схема такого дугового генератора представ-лена на рис. 7. Условия генерации колебаний в этой
с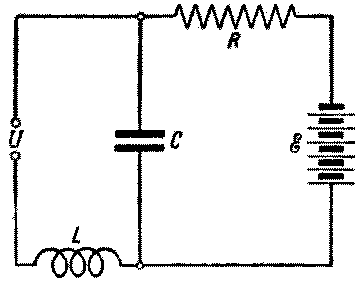
хеме можно вывести из рассмо-
трения условий устойчивости ста-
ционарного разряда при заданных
параметрах внешней цепи.
Пусть электродвижущая сила
источника постоянного тока, пи-
т
Рис. 7. Принципиальная электри-ческая схема дугового генератора.
ающего разряд (рис.7), равна ع,
напряжение между электродами
трубки U, сила стационарного то-
ка через разрядную трубку при данном режиме равна I, ём-кость катод-анод трубки плюс ёмкость всех подводящих прово-дов С, самоиндукция в цепи L, сопротивление, через которое подаётся ток от источника, R. При установившемся режиме постоянного тока будем иметь:
ع=Uо+IR (5)
Допустим, что этот стацийнарный режим нарушен. Разрядный
ток в какой-либо данный момент времени равен I+i, где i—малая величина, а разность потенциалов между электродами равна U.
Введём обозначение
U′=dU/dI
(dU/di)i=0 равно тангенсу угла наклона касательной к вольтамперной характеристике в рабочей точке, соответ-ствующей выбранному нами первоначально режиму (ток I). Посмотрим, как будет дальше изменяться i. Если i будет возрастать, то данный режим разряда неустойчив; если, наоборот, i беспредельно убывает, то режим разряда устой-чивый.
Обратимся к вольтамперной характеристике рассматриваемого
разрядного промежутка U=f(I+i)- Через трубку идёт ток
I+i и ёмкость С заряжается (или разряжается). Разность
потенциалов на ёмкости С уравновешивается в этом случае
не только напряжением на разрядном промежутке, но и э.д.с.
самоиндукции цепи. Пусть I+i2 —общий ток через сопротивле-
ние R. Обозначим ток, заряжающий ёмкость С, через i1; мгно-
венное значение разности потенциалов на ёмкости С— через U1.Разность потенциалов между электродами дуги будет U0+iU’.
Имеем:
ع=U1+(i+I2)R, (6)
U1-U0=U’i+Ldi/dt, (7)
i2=i1+i. (8)
Добавочный заряд Q на ёмкости С по сравнению со стационарным режимом:
Q=∫i1dt=(U1-U0)C. (9)
Вычитая (5) из (6), находим:
U1-U0=-i2R (10)
Выражения (7), (8) и (10) дают:
U'i+Ldi/dt=-R(i+i1). (11)
Выражения (7) и (9) дают:
1/C∫i1dt=U’i+Ldi/dt. (12)
Дифференцируя (12) по t и вставляя результат в (11), находим:
U’i+Ldi/dt=-iR-RCU’di/dt-RLCdІi/dtІ. (13)
или
dІi/dtІ +(1/CR+U’/L)di/dt +1/LC(U’/R+1)i=0 (14)
Формула (14) представляет собой дифференциальное уравнение,
которому подчиняется добавочный ток i.
Как известно, полный интеграл уравнения (14) имеет вид:
i=А1е^r1t+А2е^r2t, (15)
г![]() де r1 и r2— корни характеристического уравнения, опре-деляемые формулой
де r1 и r2— корни характеристического уравнения, опре-деляемые формулой
r=-1/2(1/CR+U’/L)+√1/4(1/CR+U’/L)І-1/LC(U’/R+1). (16)
Если подкоренная величина в (16) больше нуля, то r1 и r2
оба действительны, i изменяется апериодически по экспо-ненциальному закону и решение (15) соответствует апериодическому изменению тока. Для того чтобы в рас-сматриваемой нами схеме возникли колебания тока, необ-ходимо, чтобы r1 и r2 были комплексными величинами, т. е. чтобы
1/LC(U’/R+1)>1/4(1/CR+U’/L)І (17)
В этом случае (15) можно представить в виде
i=A1e-δt+jωt+ A2e-δt-jωt, (18)
г![]() де
де
δ=1/2(1/CR+U’/L); i=√-1.
При δ < 0 колебания, возникшие в рассматриваемой цепи, будут раскачиваться. При δ > 0 они быстро затухают, и разряд на постоянном токе будет устойчив.
Таким образом, для того чтобы в рассматриваемой схеме в конечном итоге могли установиться незатухающие колебания, надо, чтобы
(1/CR+U’/L)<0. (19)
Так как Р, L и С существенно положительные величины, то
неравенство (19) может быть соблюдено только при условии:
dU/di=U’<0. (20)
Отсюда заключаем, что колебания в рассматриваемом контуре
могут возникнуть только при падающей вольтамперной характе-
ристике разряда.
Исследование условий, при которых r1 и r2 действительны
и оба меньше нуля, приводит к условиям устойчивости разряда
постоянного тока:
(1/CR+U’/L)>0 и(21)
U’/R+1>0. (22)
Условия (21) и (22) представляют собой общие условия
Устойчивости разряда, питаемого постоянным напряжением. Из
(21) следует, что при возрастающей вольтамперной характе-
ристике разряд всегда устойчив.
Объединяя это требование с условием (22), находим, что
при падающей характеристике разряд может быть устойчивым
только при
|U’| При непосредственном применении формул этого параграфа к вопросу о генерации колебаний при помощи дуги приходится брать U' из «средней характеристики», построенной на основании восходящей и нисходящей ветвей динамической характеристики. При периодическом изменении силы тока в дуге Петрова из- меняются температура и плотность газа и скорости аэродина-мических потоков. При подборе соответствующего режима эти изменения приводят к возникновению акустических колебании в окружающем воздухе. В результате получается так называ-емая поющая дуга, воспроизводящая чистые музыкальные тона. 6. С увеличением давления газа и с увеличением плотности тока температура по оси положительного столба, отшнуровав-шегося от стенок разрядной трубки, поднимается все больше и больше. Процессы ионизации начинают принимать характер, всё более и более соответствующий чисто термической ионизации. Средняя кинетическая энергия электронов плазмы приближается к средней кинетической энергии частиц нейтрального газа. Плазма становится близкой по своим свойствам к изотерми- ческой плазме. Всё это позволяет решать задачу о нахождении различных параметров разряда, в том число продольного градиента поля в зависимости от плотности разрядного тока, на основании термодинамических соотношений. Исходными положениями теории положительного столба дуго- вого разряда при высоком и сверхвысоком давлении служит уравнение Сага для термической ионизации в виде αІp=AT5/2e-eUi/kT (24) и теорема Больцмана в виде соотношения na=nge(-eUa/kT) (25) Здесь α—степень ионизации, р—давление газа, А—постоянная, Т—температура газа, Ui—потенциал ионизации, k—постоянная Больцмана, «na —концентрация возбуждённых атомов, n—концен- трация нормальных атомов, Ua—потенциал возбуждения, g—отно- шение статистических весов ga/gn возбуждённого и нормаль-ного состояния атома. Температура электронного газа принимается равной температуре нейтрального газа. Для упрощения задача учитывает лишь один «усреднённый» уровень возбуждения. Разрядная трубка предполагается расположенной вертикально.В любом другом положении конвекционные потоки газа искажают осевую симметрию режима газа. Обозначим внутренний радиус разрядной трубки через R1, расстояние какой-либо точки от оси трубки—через r. Проведём на расстоянии одного сантиметра один от другого два сече-ния, перпендикулярные к оси трубки, и выделим между ними элементарный объём при помощи двух концентрических цилин-дров с радиусами r и r+dr(рис. 8). Обозначим количество энергии, выделяемой разрядом в единицу времени, приходя-щееся на единицу длины трубки, через N1, а количество энергии, приходящееся на рассматриваемый нами элементарный объём,—через dN1. Количество энергии, излучаемой в едини-ц в единице длины всей трубки и в рассматриваемом элементарном объёме, обозначим через S1 и dS1. Внутри трубки существует н Рис. 8. Элемент объема в аксиально-сим-метрическом разряде.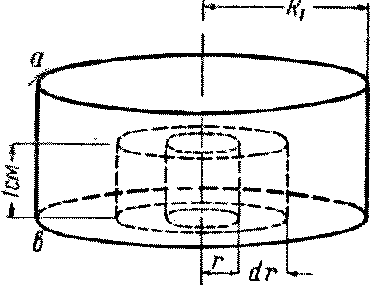
у времени газом, заключённым
епрерывный радиальный поток
тепла через газ по направлению
от оси к стенке. Обозначим че-рез dL1 избыток количества тепла, покидающего в единицу времени рассматриваемый элемент объёма через его внешнюю границу, над количеством тепла, проникающего в тот же объём в единицу времени через его внутреннюю границу со стороны оси трубки. Допустим, что конвекционные потоки газа строго вертикальны и не нарушают теплового режима газа.
Условие теплового баланса рассматриваемого элементарного
объёма напишется в общем виде так:
dN1=dL1+dS1. (26)
Вследствие наличия осевой симметрии все величины, характе-
ризующие состояние газа и режим разряда, одинаковы для
точек, находящихся на одном и том же расстоянии r от оси.
Так как площадь основания рассматриваемого элементарного
объёма равна 2пrdr, то для мощности, выделяемой в этом
объёме, можем написать:
dN1=2пrirEzdr, (27)
нде ir-плотность тока на расстоянии r от оси, а Ez-про-дольный градиент поля, одинаковый по всему поперечному сечению трубки. Обозначая коэффициент теплопроводности газа при температуре Т через λт, напишим для dL1, пренебрегая членами высшего порядка малости:
dL1=2п(r+dr)(λтdT/dr)r+dr-2пr(λтdT/dr)r=2пd(rλтdT/dr)/dr (28)
Допустим, что излучаемая газом энергия целиком покидает
разрядный промежуток без заметной реабсорбции в газе. Такое
допущение можно сделать потому, что абсорбируемое газом резонансное излучение составляет при большом давлении лишь незначительную долго общего излучения газа. Так как излу-чаемая за единицу временя энергия пропорциональна концен-трации возбуждённых атомов na, то для dS1 можем написать:
dS1=2пrCnadr, (29)
где С—постоянный множитель, не зависящий от Т. Подстановка
значений (29) и (28) в (26) даёт:
2пrirEzdr=2пd(rλтdT/dr)dr/dr + 2пrCnadr (30)
Пренебрегая малой долей тока, приходящейся на долю поло-
жительных ионов, и обозначая подвижность электронов через Кe, можем написать:
i=neeKeEz. (31)
Если обозначим правую часть уравнения Сага (24) через f1(T), а р в левой части заменим через nkТ, где n — концен-трация нейтральных частиц газа, то найдём:
α2= f1(T)/ nkТ. (32)
n пропорционально массе газа, заключённого в единице длины
трубки, g1 и обратно пропорционально квадрату радиуса труб-ки R1 и температуре газа в данной точке:
n=C1g1/TR12 (33)
П![]()
![]()
![]() оэтому вместо (32) можем написать:
оэтому вместо (32) можем написать:
α=R1√f1(T)/C1k/√g1 =R1f2(T)/√g1 (34)
Согласно уравнению Ланжевена скорость движения электрона
в![]() газе в поле напряжённости Еz равна:
газе в поле напряжённости Еz равна:
u=KeEz=aeλeEz/mv (35)
г![]() де v— средняя арифметическая скорость теплового движения
де v— средняя арифметическая скорость теплового движения
электронов, прямо пропорциональная квадратному корню из температуры электронного газа, в то время как λe обратно пропорционально n. Следовательно,
Ke=C2/nT1/2 (36)
Согласно определению величины α:
ne=αn (37)
Из (31), (34), (37) и (36) следует:
ir=EzRiC2f2(T)/g11/2 T1/2 (38)
где Т—температура газа на расстоянии r от оси. Из (38)
и (27) следует:
dN1=2пrEr2R1C2f2(T)dr/g11/2 T1/2=2пrEz2R1f3(T)dr/g11/2,(39)
Согласно уравнению Больцмана (25):
na=nge(-eUa/kT)=C1gg1e(-eUa/kT)/TR12=g1f4(T)/ R12, (40)
где f4(T)= C1ge(-eUa/kT)/T.
Вставляя это значение na в (29) и заменяя Сf4(Т) через f5(Т), находим:
dS1=g12пrf5(Т)dr/R12. (41)
Подстановка (39), (28) и (41) в (26) даёт
Er2R1f3(T)/g11/2=d(rλтdT/dr)/rdr+g1f5(Т)dr/R12 (42)
В уравнении (42) f3(T) и f5(T), а также λт-функции одного только переменного Т. Поэтому (42) представляет собой
дифференциальное уравнение, связывающее переменные Т и r.
Граничными условиями, которым должно удовлетворять решение
этого уравнения, являются: а) при r=R условие Т=Тст, где Тст — температура стенки разрядной трубки; б) при r=0 условие dT/dr = 0, так как на оси трубки температура газа имеет максимальное значение.
Все величины, характеризующие разряд, являются функциями
от одного только Т. Поэтому решение уравнения (42) могло
бы дать полное решение всех количественных вопросов, связанных с данным типом разряда. Однако значение уравнения (42) заключается главным образом в том, что путём перехода к безразмерным величинам оно приводит к характерным для данного типа разряда законам подобия, позволяющим перено-сить количественные результаты, установленные эксперимента-льно для одних значений N1, R1 и g1 на режим разряда при других значениях этих величин. Этот приём аналогичен тому, который применяется для решения некоторых задач гидродина-мики также лишь на основании анализа дифференциального уравнения и экспериментальных измерений на моделях, постро-енных в соответствии с законами подобия гидродинамики. В данном случае подобными являются два разряда, в которых в соответственных точках, характеризуемых одной и той же величиной отношения r/R1, температура газа одна и та же.
Практически наиболее существенными являются следующие
два закона подобия:
Первый закон подобия отшнурованного дугового разряда высокого давления. Два дуговых разряда высокого давления в цилиндрических трубках различного диаметра (2R1 ≠ 2R1'), наполненных газом так, что на один сантиметр длины той и другой трубки приходится одно и то же количество газа (g1=g1’), являются подобными в том случае, если N1=N1’,т. е. если расходуемые мощности на единицу длины трубки в обоих случаях одинаковы.
Второй закон подобия отшнурованного дугового разряда высокого давления. Два дуговых разряда высокого давления в парах ртути в цилиндрических трубках различного диаметра (2R1 ≠ 2R1'), наполненных парами ртути так, что на один сантиметр длины каждой из трубок приходятся различные коли-чества паров ртути (g1≠g1’), являются подобными, если расходуемые на единицу длины каждой трубки мощности N1 и N1’ удовлетворяют соотношению
N1/N1’=8,5+5,7g1/8,5+5,7g1’ (43)
При этом предполагается, что ртуть в разряде полностью перешла в парообразное состояние. Ко
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Жан Батист Жозеф Фурье
Жан Батист Жозеф Фурье.(21.3.1768-16.5.1830) Французский математик,член Парижской АН (1817). Окончив военную школу в Осере, где родился, работал там ж
- Железные Дороги России
Системы электроснабжения электрифицированных железных дорог по предъявляемым к ним требованиям, условиям работы, используемому обору
- Жизнь и деятельность А С Попова
- Законы сохранения в механике
- Занимательные опыты по физике
- Измерение неэлектрических величин
- Измерение постоянных токов
Rīgas Tehniskā UniversitāteDMZCVladimirs BernatovičsKursa darbs(Elektriskie mērījumi)Līdzstrāvas mērīšana ar šunta palīdzību2002Saturs.1. Ievads 32. Teoretiskā daļa 4 3.
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

