Экзаменационные билеты по математике
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 1
Уравнение плоскости в пространстве. Геометрический смысл его коэффициентов. Привести пример.
Что такое Пуассоновский поток событий? Привести пример его применения.
Магазин продал в первый день 60% товара, а во второй – 50% остатка. Сколько процентов товара продано за 2 дня?
Найти длину вектора 3
 – 2
– 2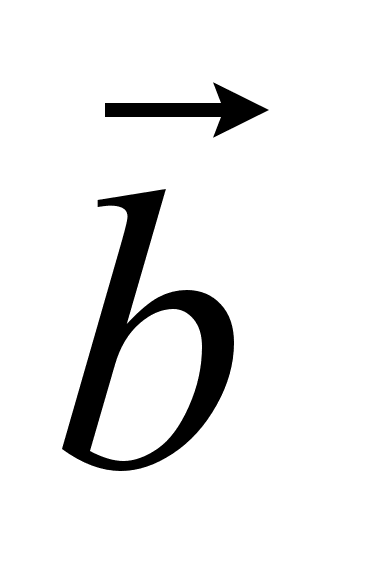 , если дано:
, если дано:  {2, -1, 7},
{2, -1, 7}, 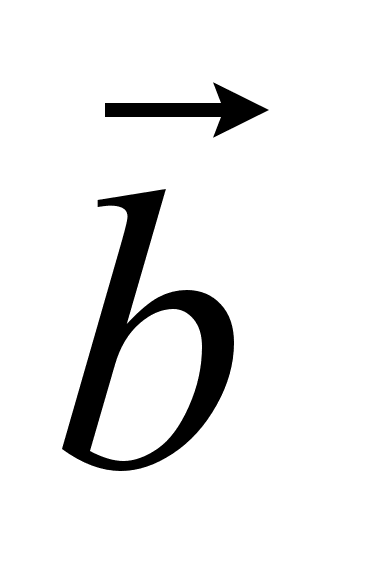 {-1, 1, 4}.
{-1, 1, 4}.Найти интервалы монотонности функции ƒ(х) = 2х3 + 3х2 –36х -2.
Для независимых нормальных случайных величин X~N(3,4) и Y~N(5,3). найти
М(x+y), М(x-y) и D(x+y), D(x-y).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 2
Дать определение арифметической прогрессии. Написать формулы для
п-го члена прогрессии и суммы первых п членов. Привести пример применения этих формул.Определение первообразной и неопределенного интеграла функции. Привести пример.
В первую сессию торгов акции компании подорожали на 40%, во вторую подешевели на 30% к первой. На сколько процентов изменилась цена акции за 2 сессии?
Написать уравнение параболы с вершиной в начале координат и горизонтальной директрисой, причем парабола проходит через точку (1, -5).
Найти производную функции ƒ(х) =
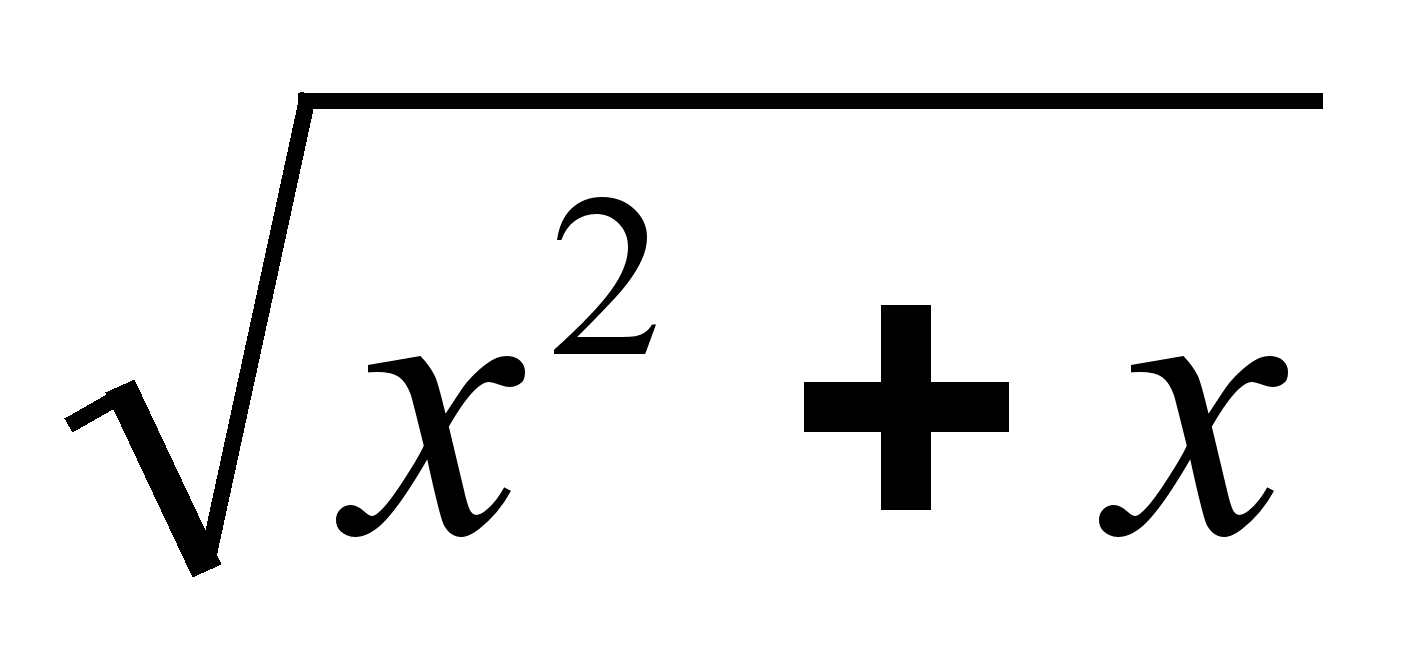 .
.Случайная величина Х задана рядом распределения:

Найти D(X+3).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 3
Общее уравнение прямой на плоскости. Как выглядит общее уравнение вертикальной и горизонтальной прямой?
Что такое дискретная случайная величина? Какими данными она задается? Привести пример.
Известно, что высказывания a, – истинны, а с – ложно. Определить истинность высказывания (с

 )
) 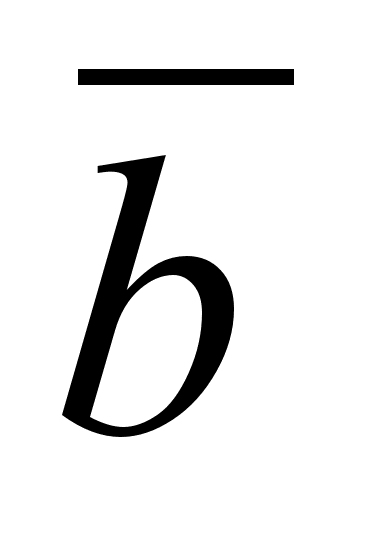 .
.Написать уравнение плоскости, проходящей через точку (1, -4, 0) перпендикулярно прямой
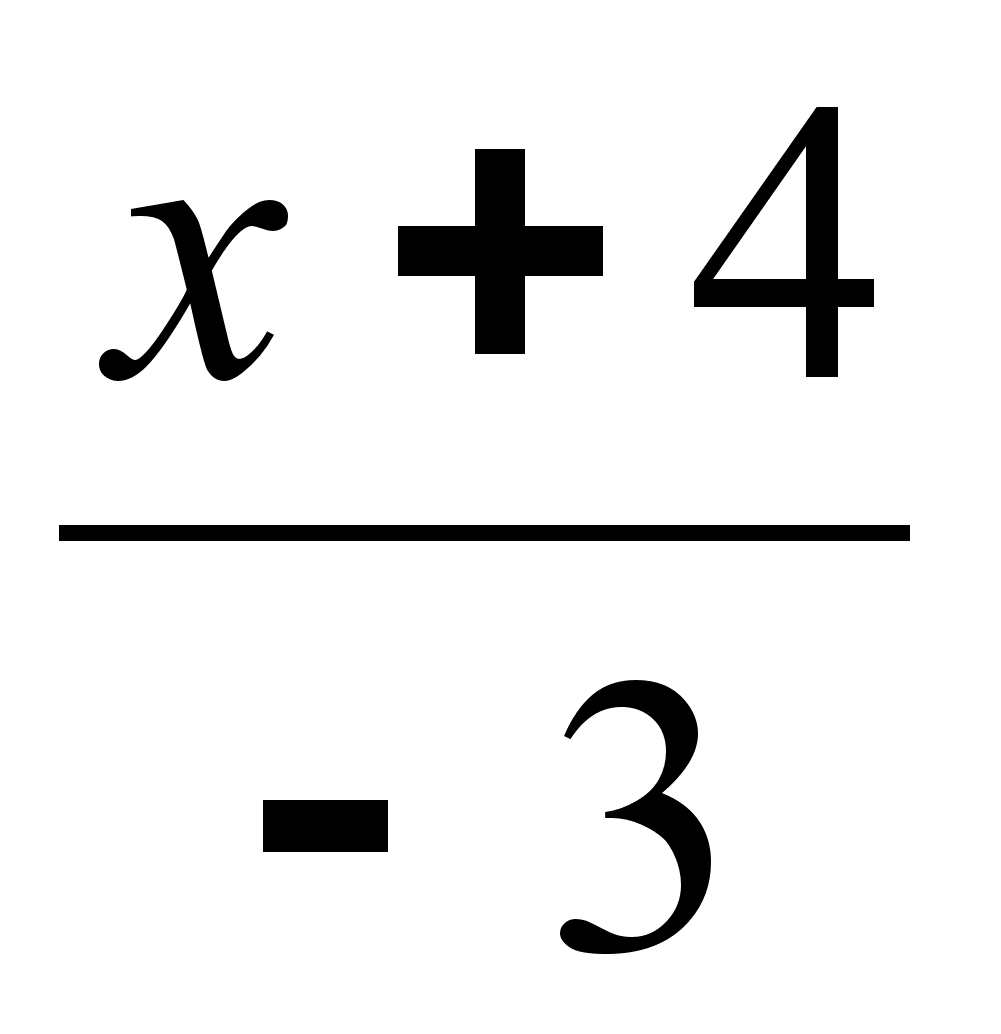 =
= 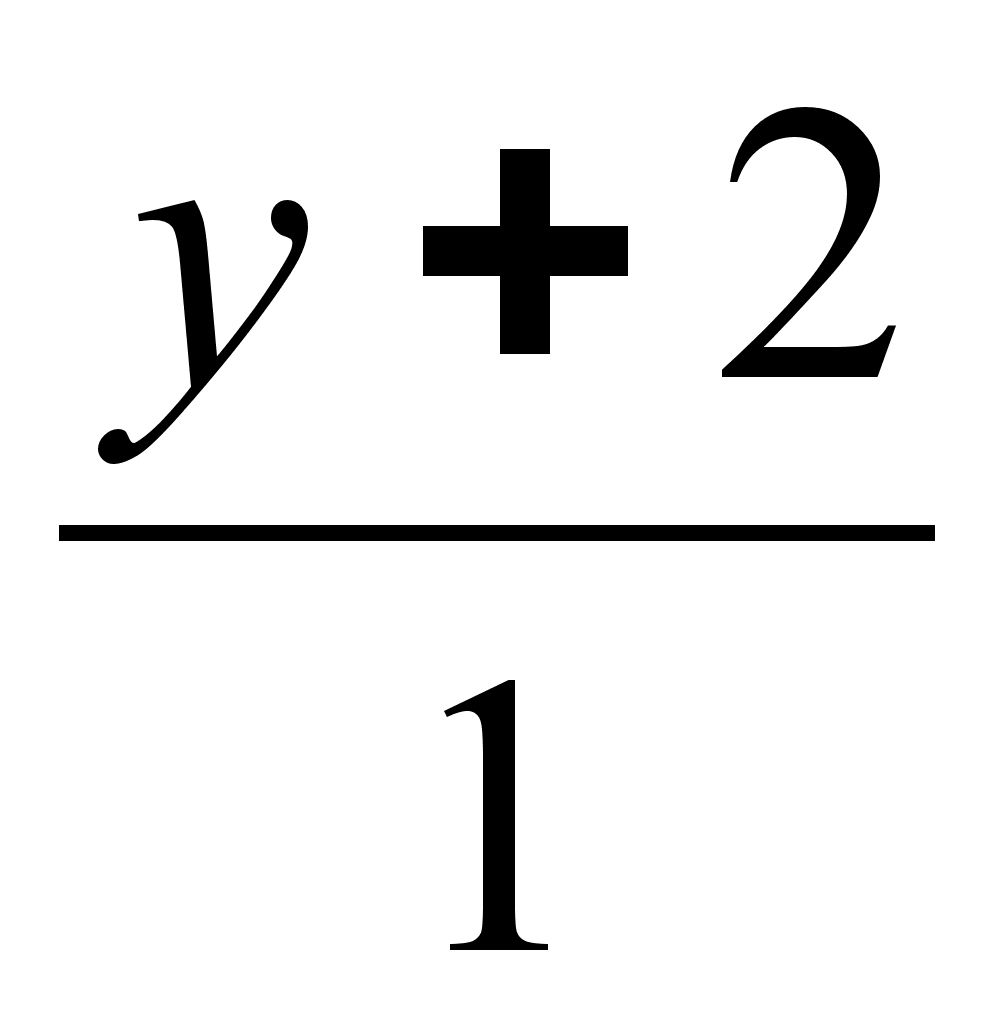 =
= 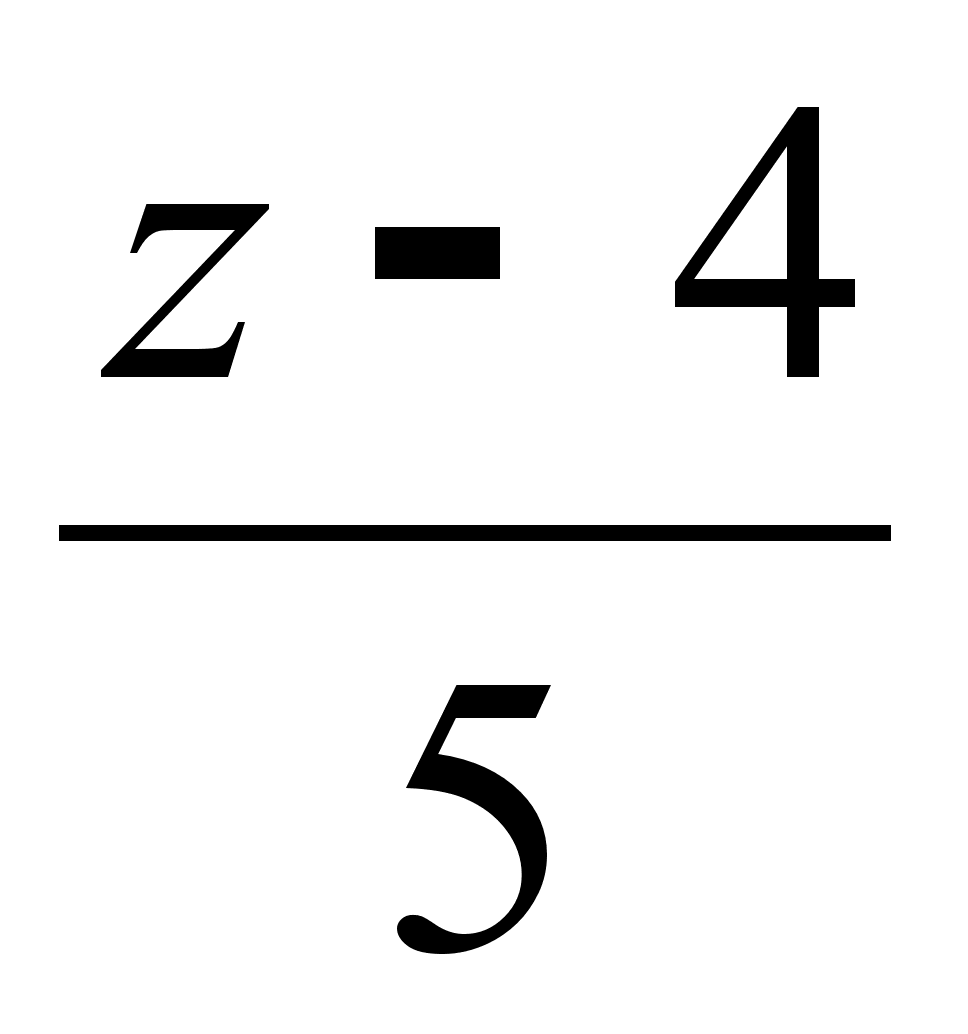 .
.Найти точки экстремума функции ƒ(х) = х4 – 8х2 - 2.
Случайная величина X задана рядом распределения:
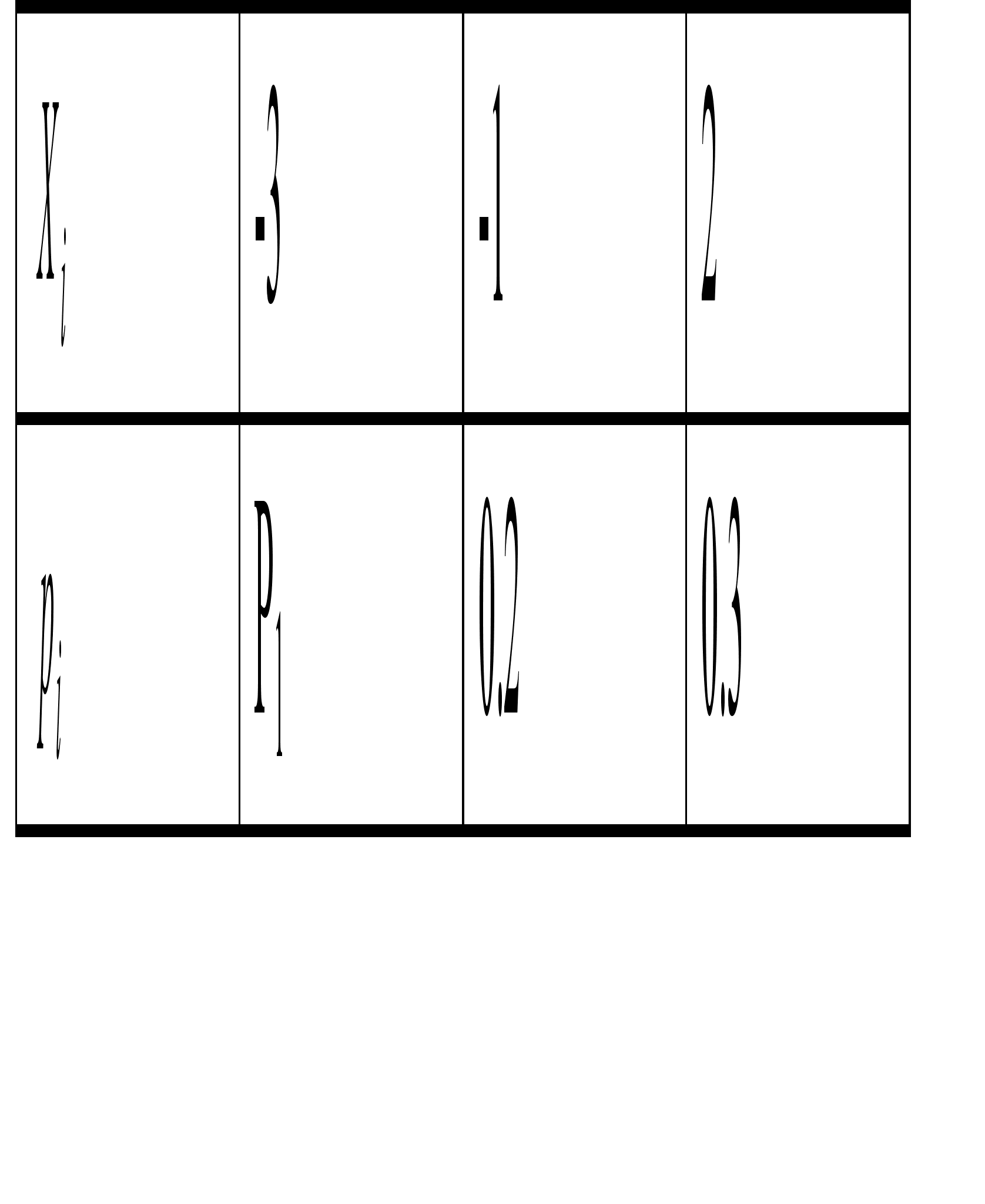
найти Р1 и D(X+3).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 4
Угол между векторами. Формула для косинуса угла в координатах. Условие ортогональности векторов.
Что такое схема Бернулли? Записать асимптотическую формулу Пуассона и объяснить, при каких условиях она применяется.
Числовая последовательность определяется следующим условием:
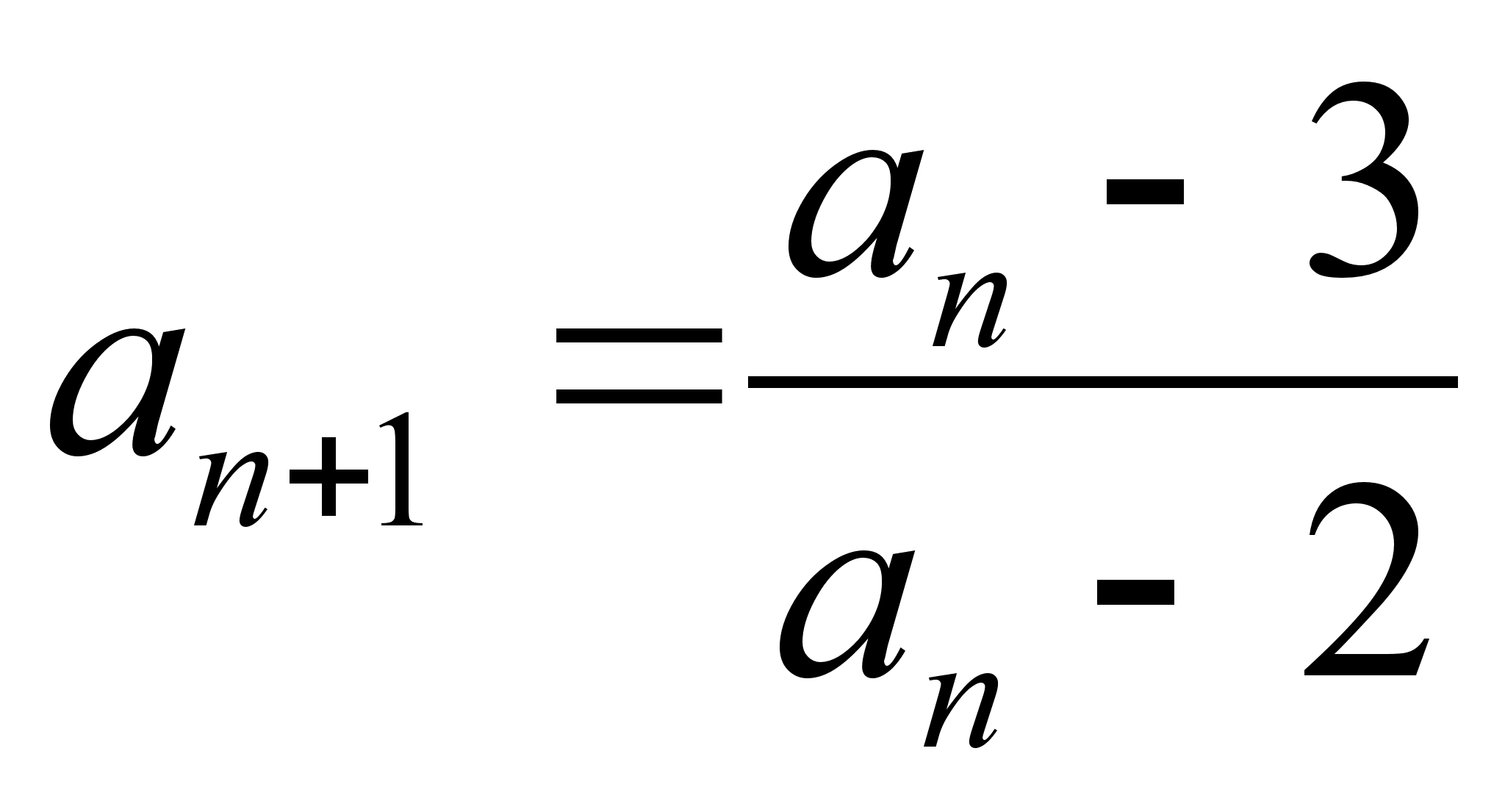 . Найти
. Найти 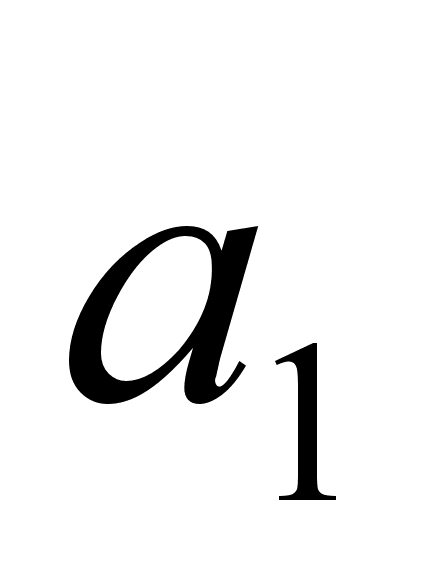 , если
, если 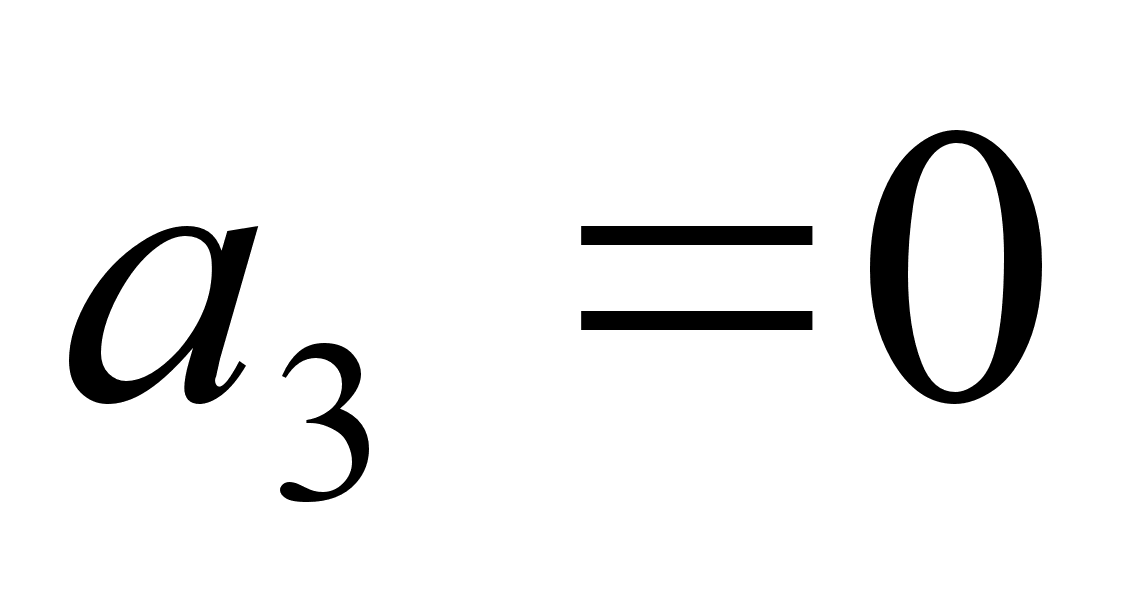 .
.Найти координаты вершин и фокусов эллипса 4х2 + 25у2 = 100.
Вычислить неопределенный интеграл
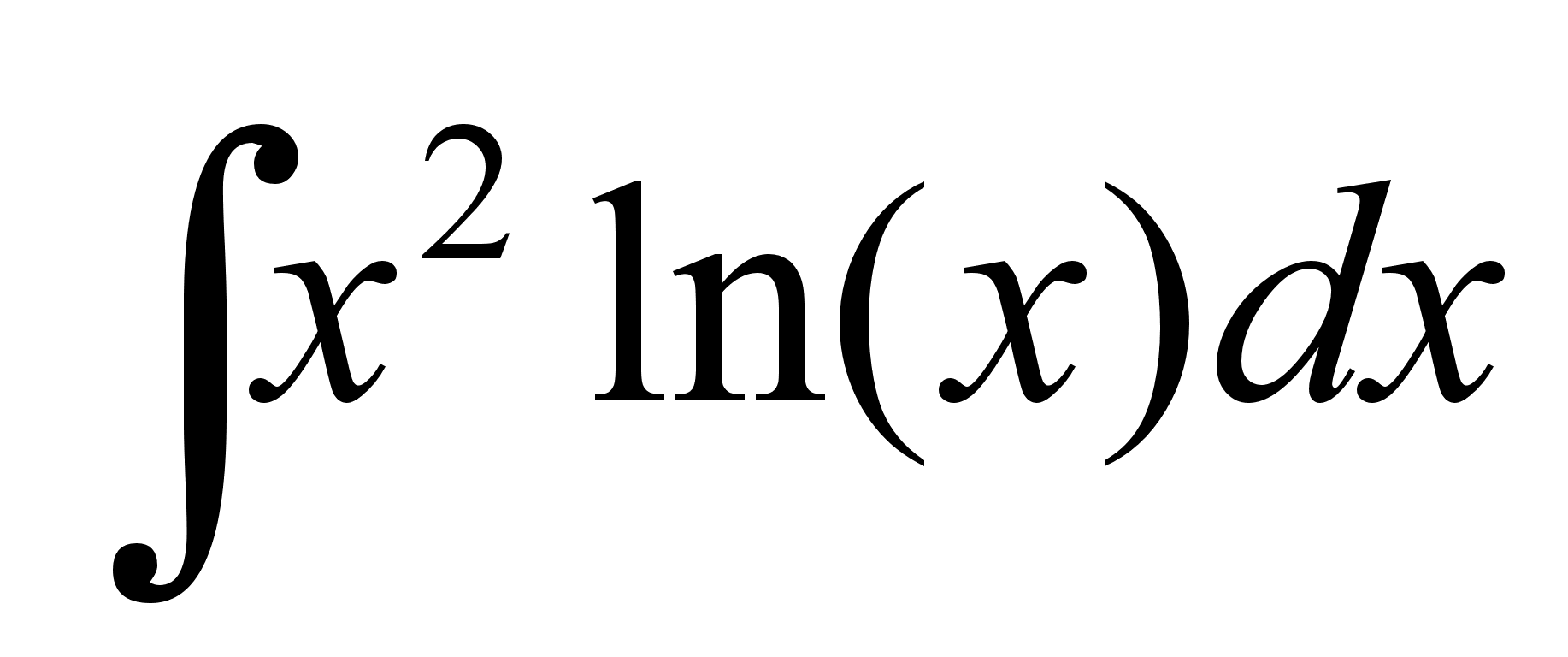 .
.К компьютерной сети подключены 100 пользователей, каждый из которых в данный момент времени работает в сети с вероятностью 0,02. Найти вероятность того, что в данный момент хотя бы один пользователь работает в сети.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 5
Дать определение разности множеств, показав его на диаграммах Венна. Привести пример разности числовых множеств.
Как вводятся числовые характеристики непрерывной случайной величины - математическое ожидание, дисперсия, среднеквадратическое отклонение? Какой смысл имеют эти характеристики?
Числовая последовательность определяется следующим условием:
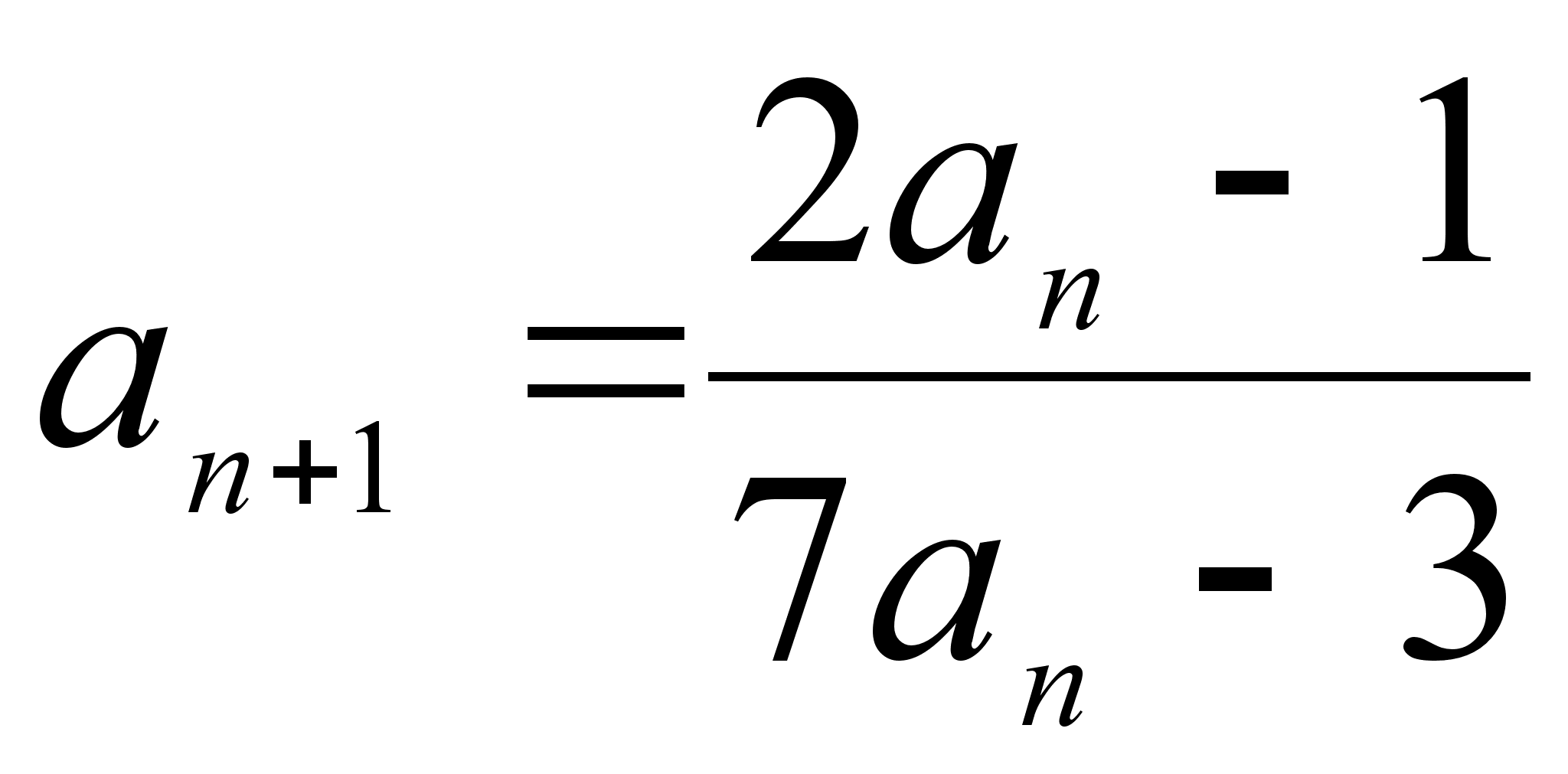 . Найти
. Найти 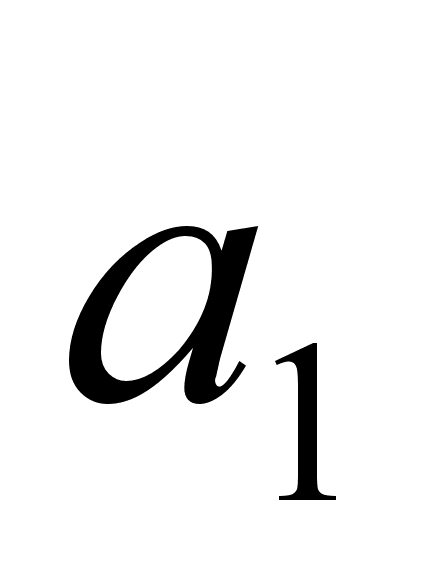 , если
, если 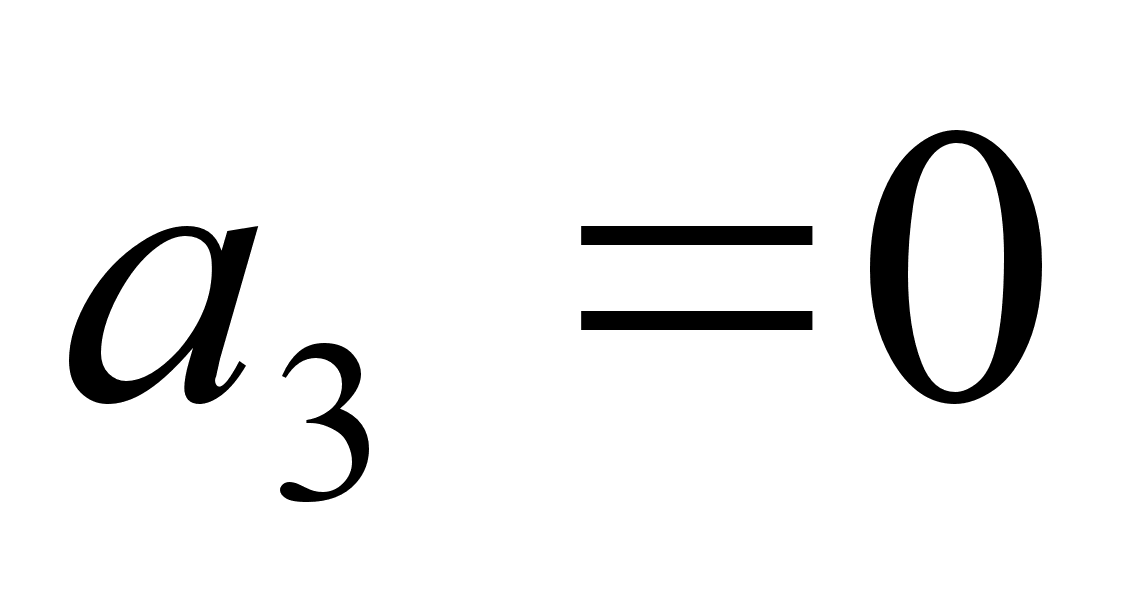 .
.Найти координаты вершин и фокусов эллипса 25х2 + 9у2 = 225.
Найти производную функции ƒ(х) = ln (
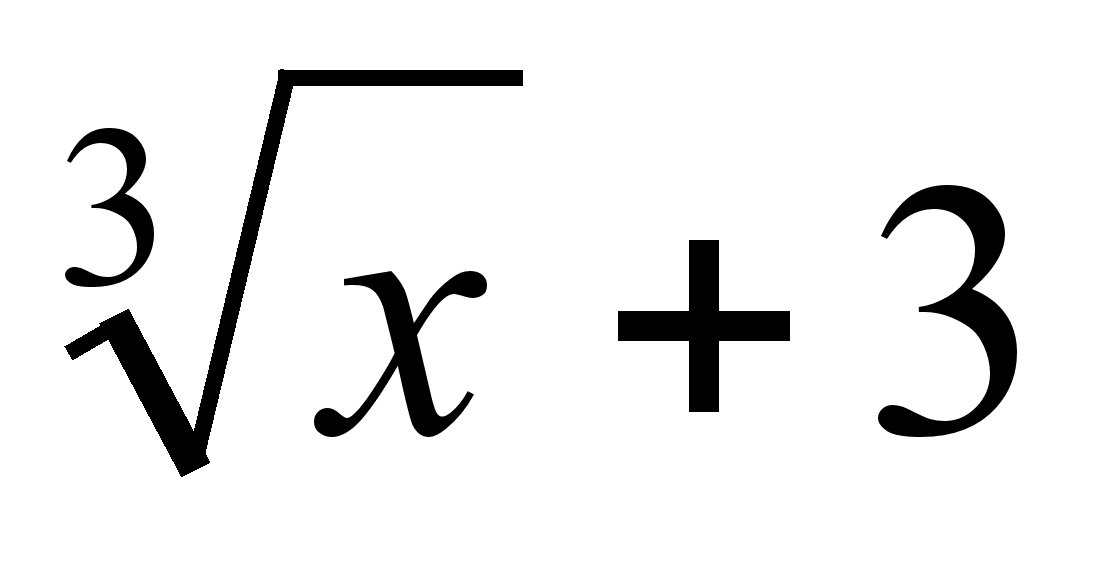 ).
).В урне 3 белых и 6 черных шаров. Наугад вынимают два шара. Найти вероятность того, что оба шара окажутся одного цвета.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 6
Параметрические и канонические уравнения прямой в пространстве. Геометрический смысл его коэффициентов. Привести пример.
Определение точки локального минимума функции. Необходимое условие минимума. Достаточное условие минимума. Привести пример применения достаточного условия.
Числовая последовательность определяется следующим условием:
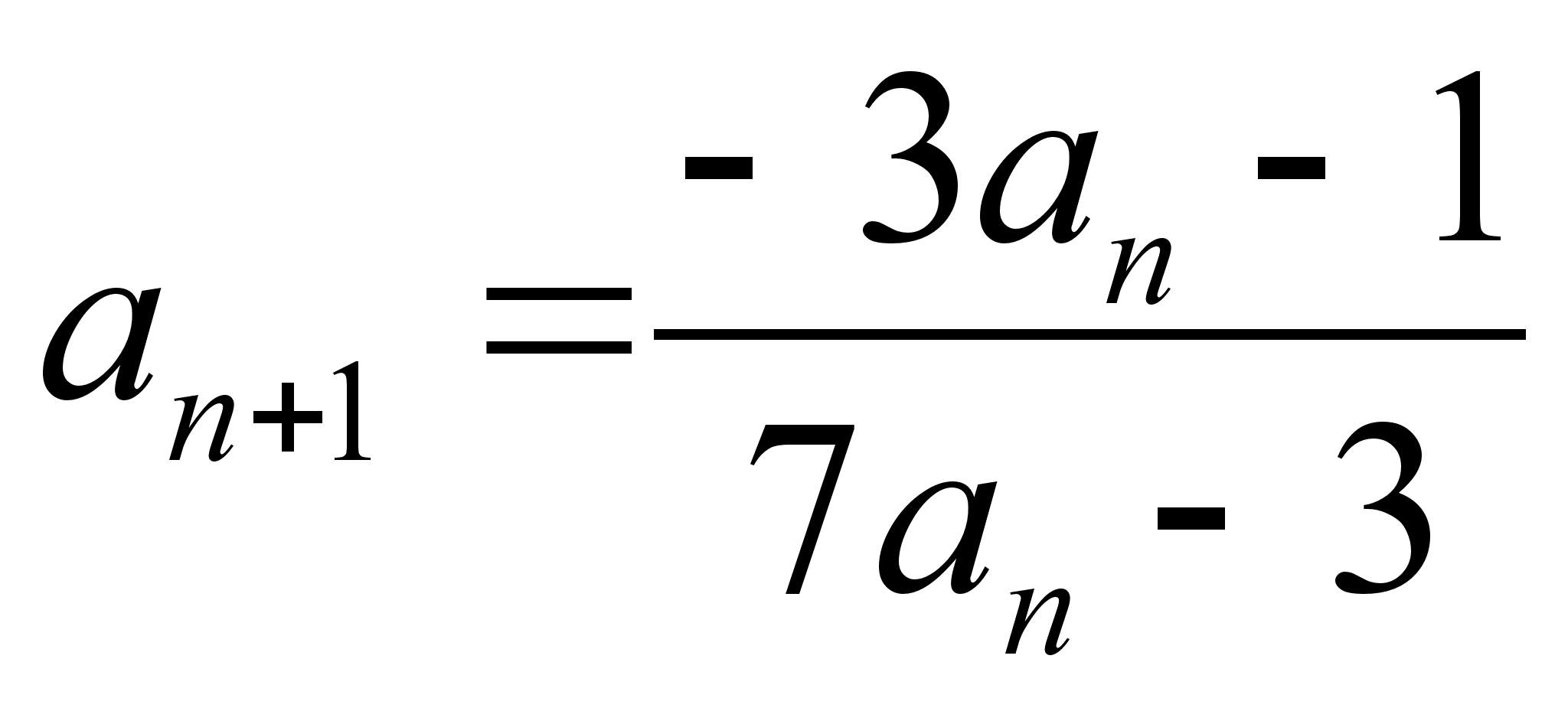 . Найти
. Найти 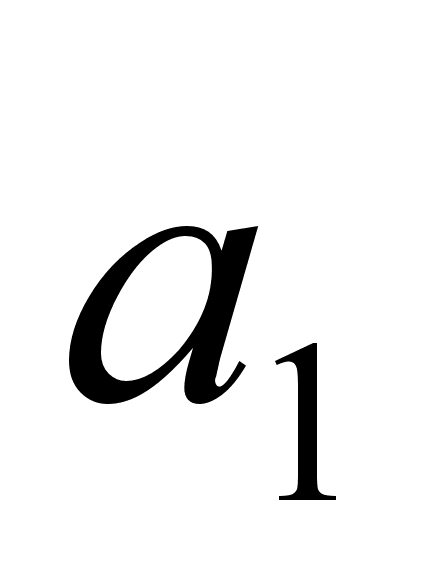 , если
, если 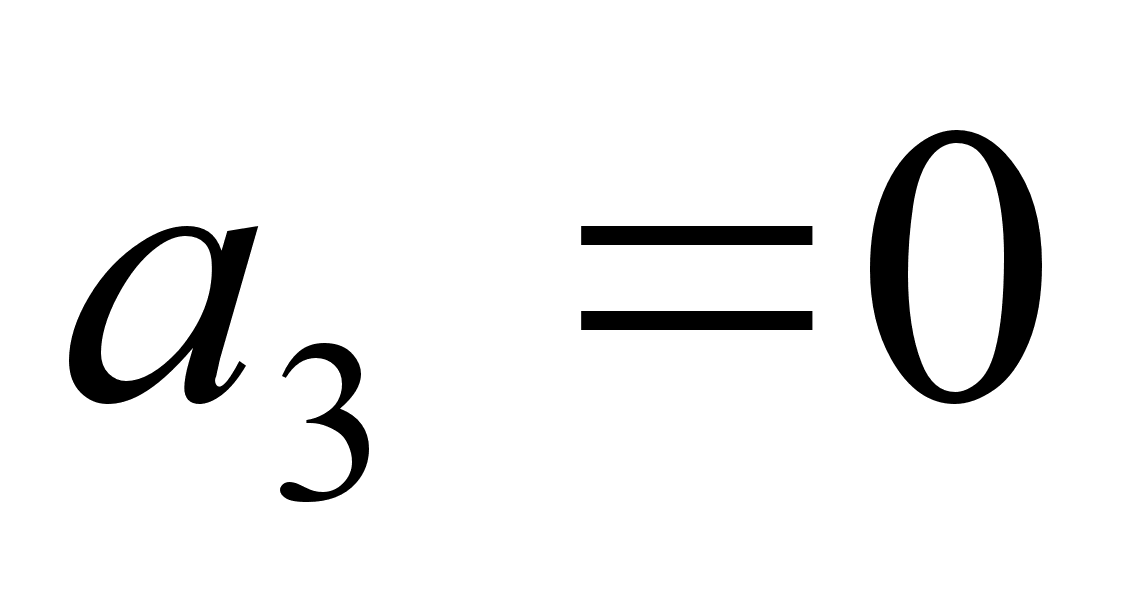 .
.Найти общее уравнение медианы треугольника АВС из точки А, если известно:
А (1, -3), В (0, 3), С (-4, 1).Вычислить площадь фигуры, ограниченной линиями
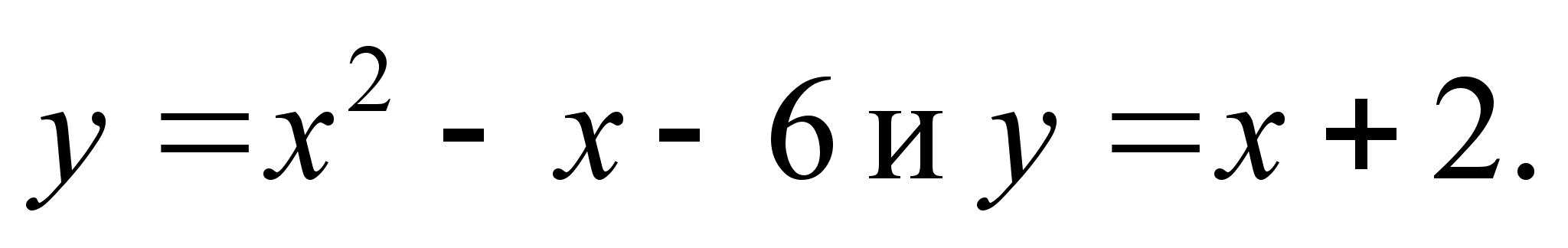 .
.В колоде 36 карт. Наугад вынимают три карты. Найти вероятность того, что вынутыми окажутся два туза и одна дама.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 7
Дать определение объединения множеств, показав его на диаграммах Венна. Привести пример объединения числовых множеств.
Определение непрерывности функции в точке и на отрезке. Точки разрыва первого и второго родов. Привести пример точки разрыва функции.
Найти сумму бесконечно-убывающей геометрической прогрессии: 6, 2,
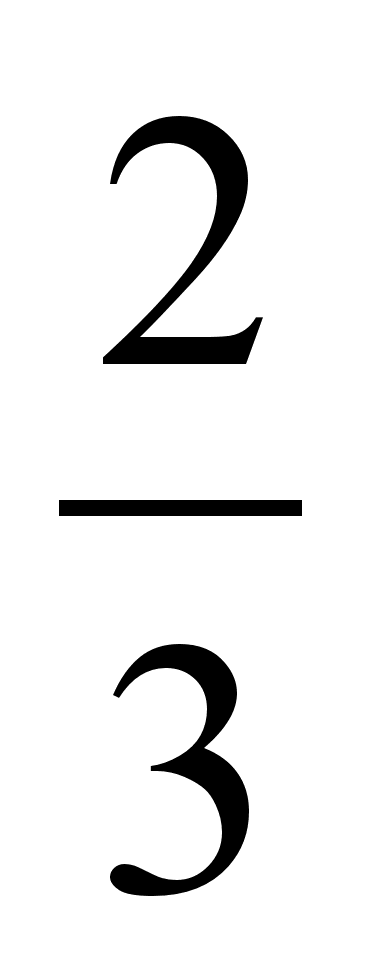 ,
, 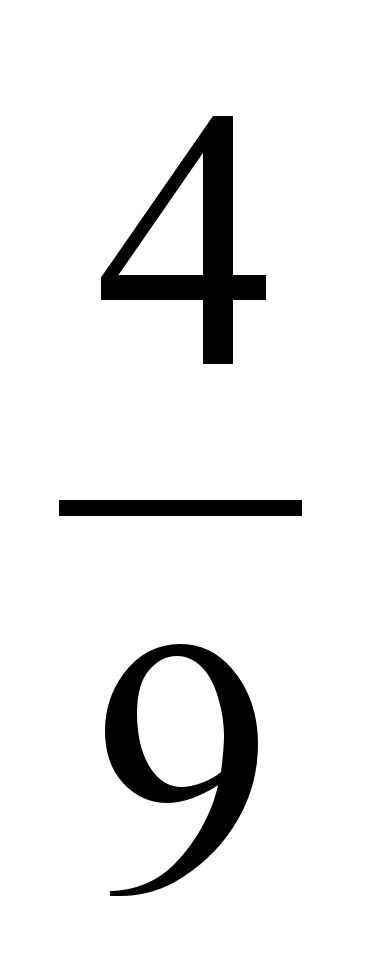 , …
, …Написать уравнение плоскости, походящей через точку А(3,1,4) параллельно плоскости 2x – 4y + 3z + 5 = 0.
Вычислить неопределенный интеграл
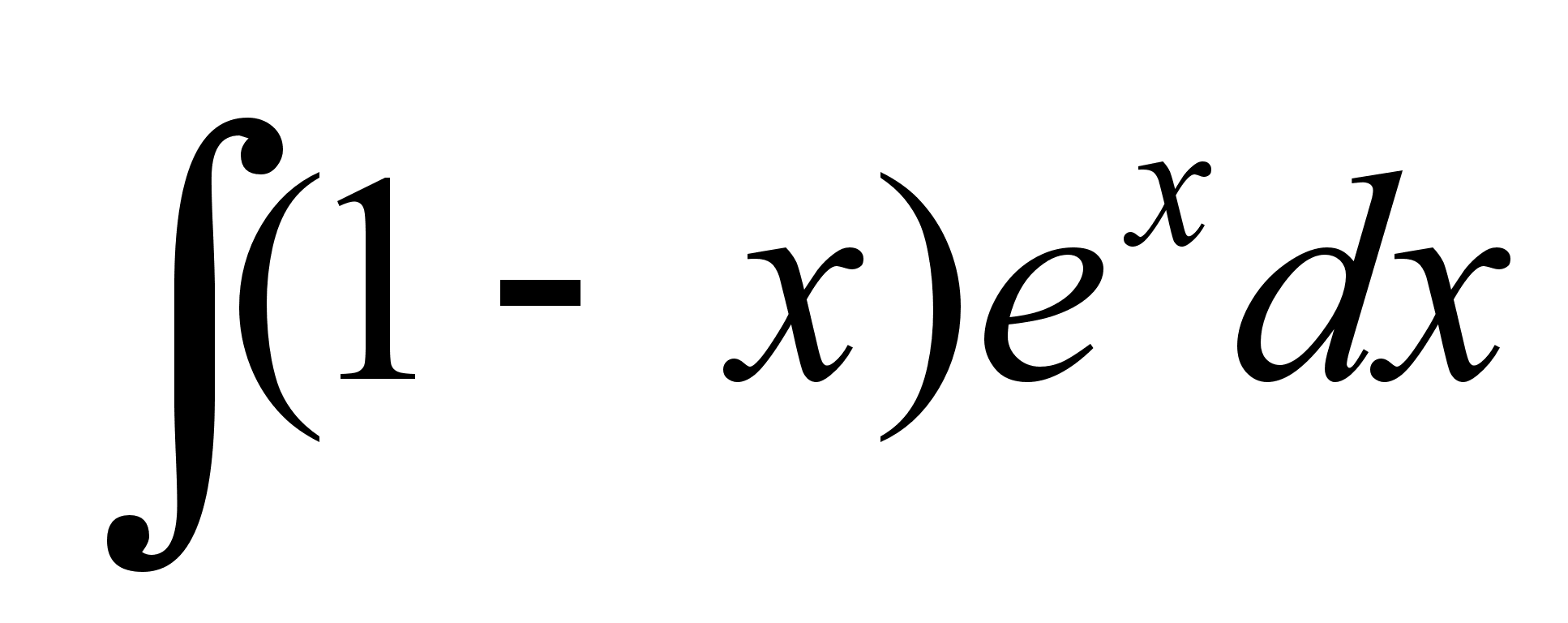 .
.Вероятность выигрыша по облигации займа равна 0,25. Какова вероятность того, что некто, приобретая 5 облигаций, выиграет хотя бы по одной из них?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 8
Угол между прямыми в пространстве. Формула косинуса угла. Привести пример применения этой формулы.
Что такое непрерывная случайная величина? Какими данными она задается? Привести пример.
Найти сумму бесконечно-убывающей геометрической прогрессии: 4, 2, 1, 0.5, …
Дано уравнение кривой в декартовых координатах: х2- у2 = 5х. Написать это уравнение в полярных координатах.
Вычислить неопределенный интеграл
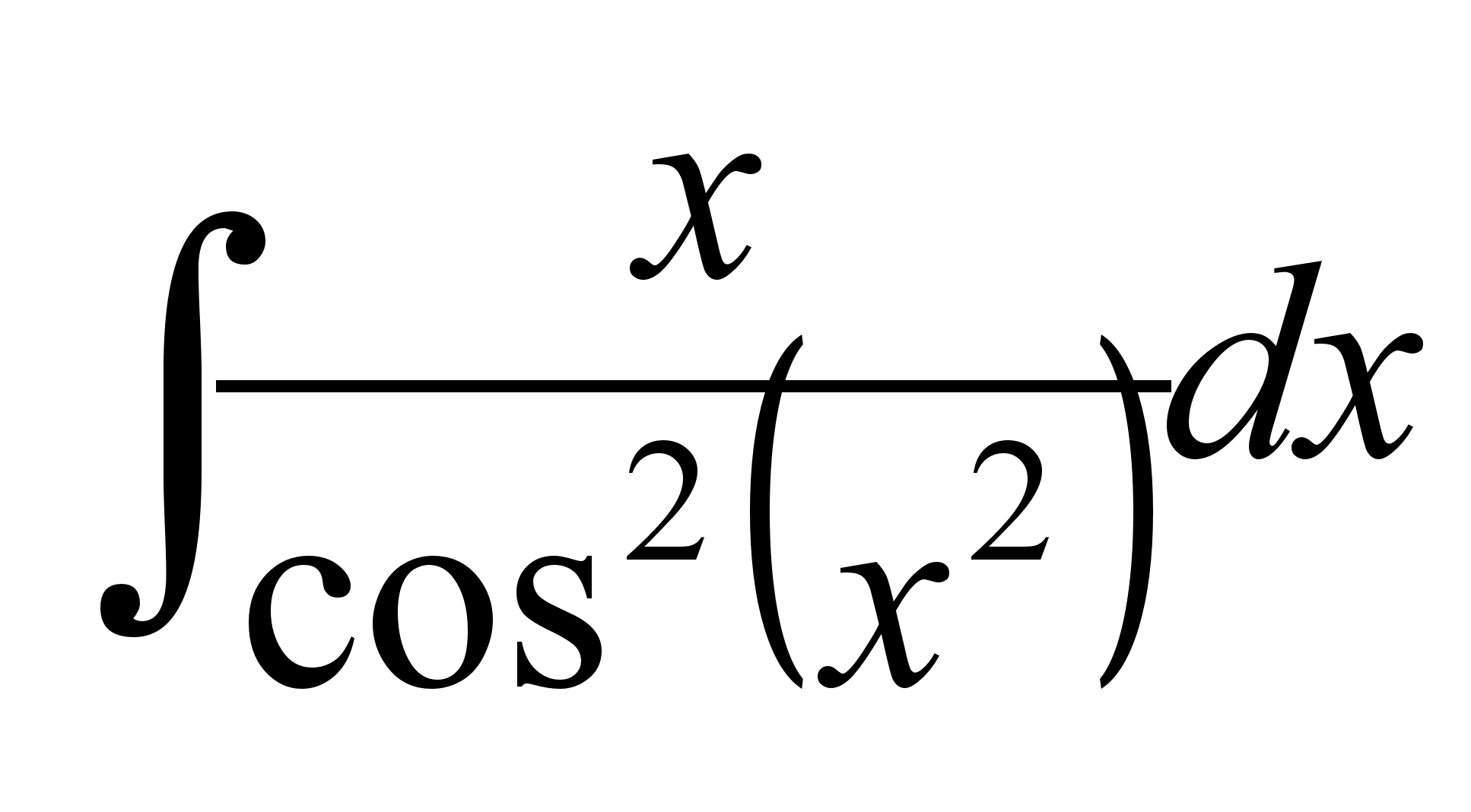 .
.Брошены две игральные кости. Найти вероятность того, что произведение выпавших очков окажется меньше 5, больше 5.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 9
Формула угла между прямыми на плоскости, заданными своими угловыми уравнениями. Условие параллельности и перпендикулярности прямых на плоскости.
Что такое стохастический (случайный) эксперимент, событие, элементарные события? Привести пример случайного эксперимента и описать в нем элементарные события.
Определить, какие из точек К (0, -4), L(-1,1), M (6, -9) принадлежат множеству
А = {(x,y) :x2+ 1 ≥ y ≥ -x -3}.Найти длину вектора
 – 3
– 3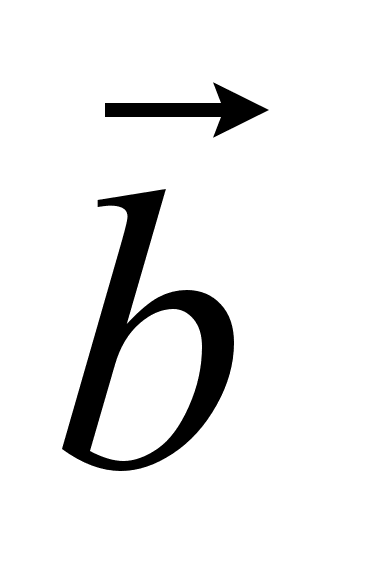 , если дано:
, если дано:  {2, -4, -1},
{2, -4, -1}, 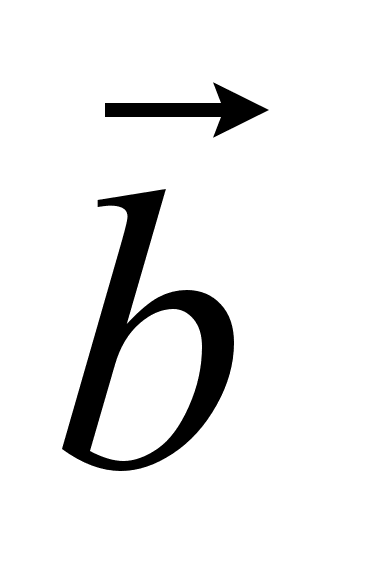 {-1, -3, 1}.
{-1, -3, 1}.Найти интервалы монотонности функции ƒ(х) = х4 – 2х2 –3.
Случайная величина X задана рядом распределения:

найти Р3 и DX.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 10
Дать определение области определения и области значений числовой функции. Описать области определения и значений функции y =
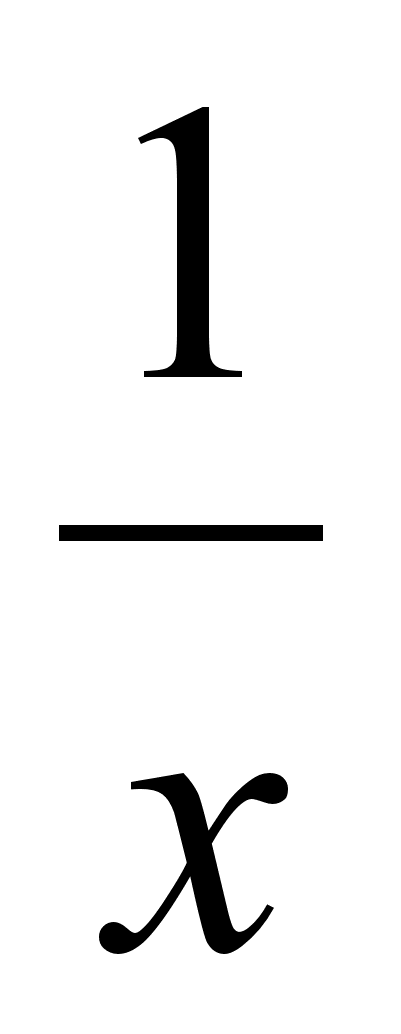 .
.Что такое схема Бернулли? Записать асимптотические формулы Муавра-Лапласа и объяснить, при каких условиях они применяются.
Даны числовые множества: А = {3х | xцелое}, В = {х2 | х целое}, С= (-2, 12). Найти
(А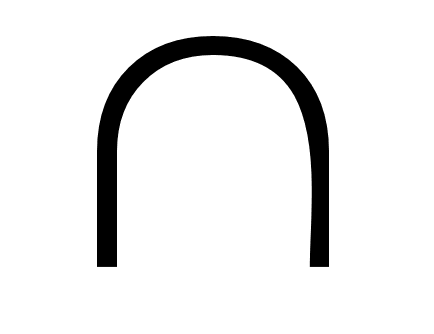 С) \ В.
С) \ В.Найти общее уравнение высоты треугольника АВС из точки А, если известно:
А (-1, 4), В (-1, 0), С (2, 1).Найти производную функции f(x) =
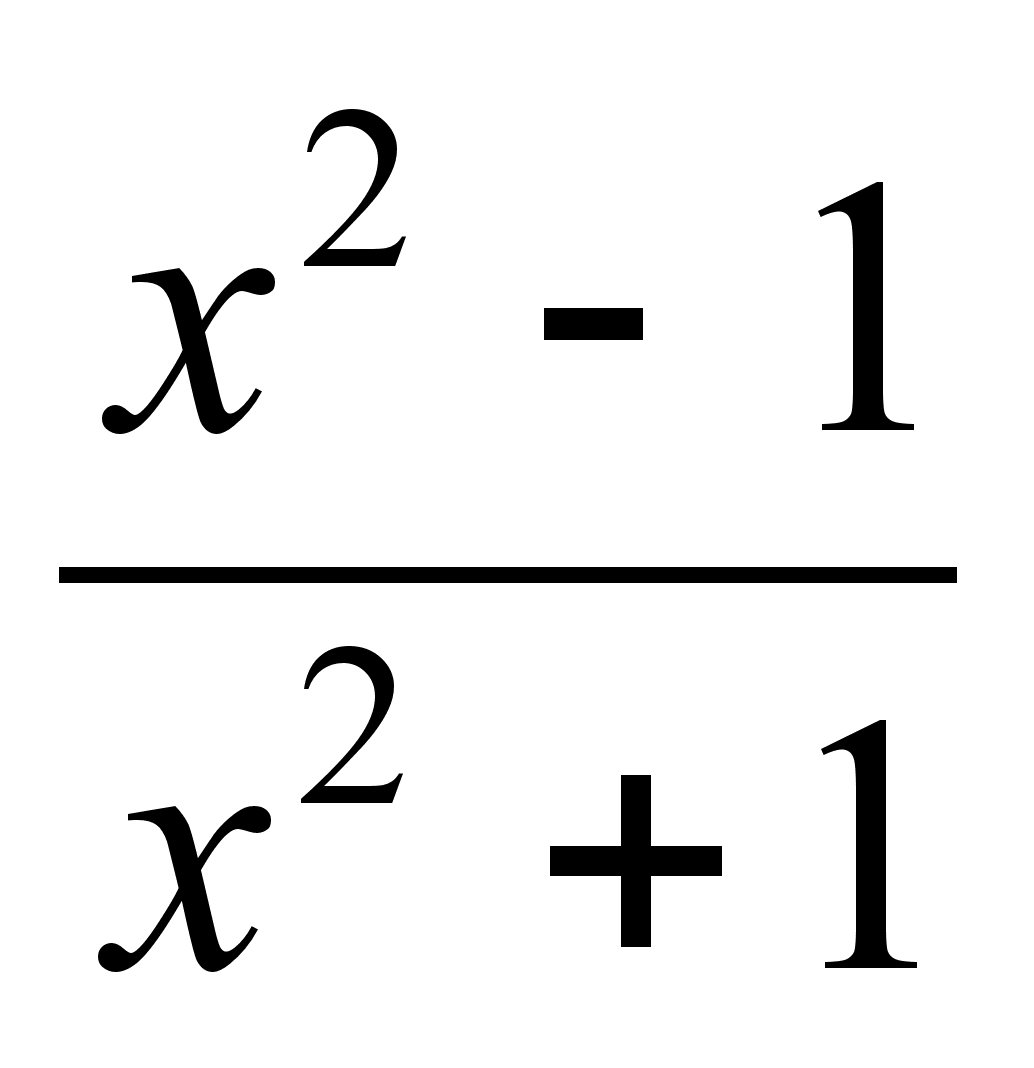 .
.Вероятность того, что денежная купюра фальшивая равна 0.001. Найти вероятность того, что среди 500 полученных Вами купюр имеется фальшивая.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 11
Каноническое уравнение гиперболы. Геометрический смысл его параметров. Формулы координат фокусов. Привести пример.
Дать определение независимых событий. Записать формулу вероятности произведения независимых событий и привести пример ее применения.
Найти сумму первых 5 членов геометрической прогрессии, если первый член равен 3, а четвертый -24.
Написать уравнение плоскости, походящей через точку А(1,0,-1) параллельно плоскости 4x + 2y - 5z - 4 = 0.
Вычислить неопределенный интеграл
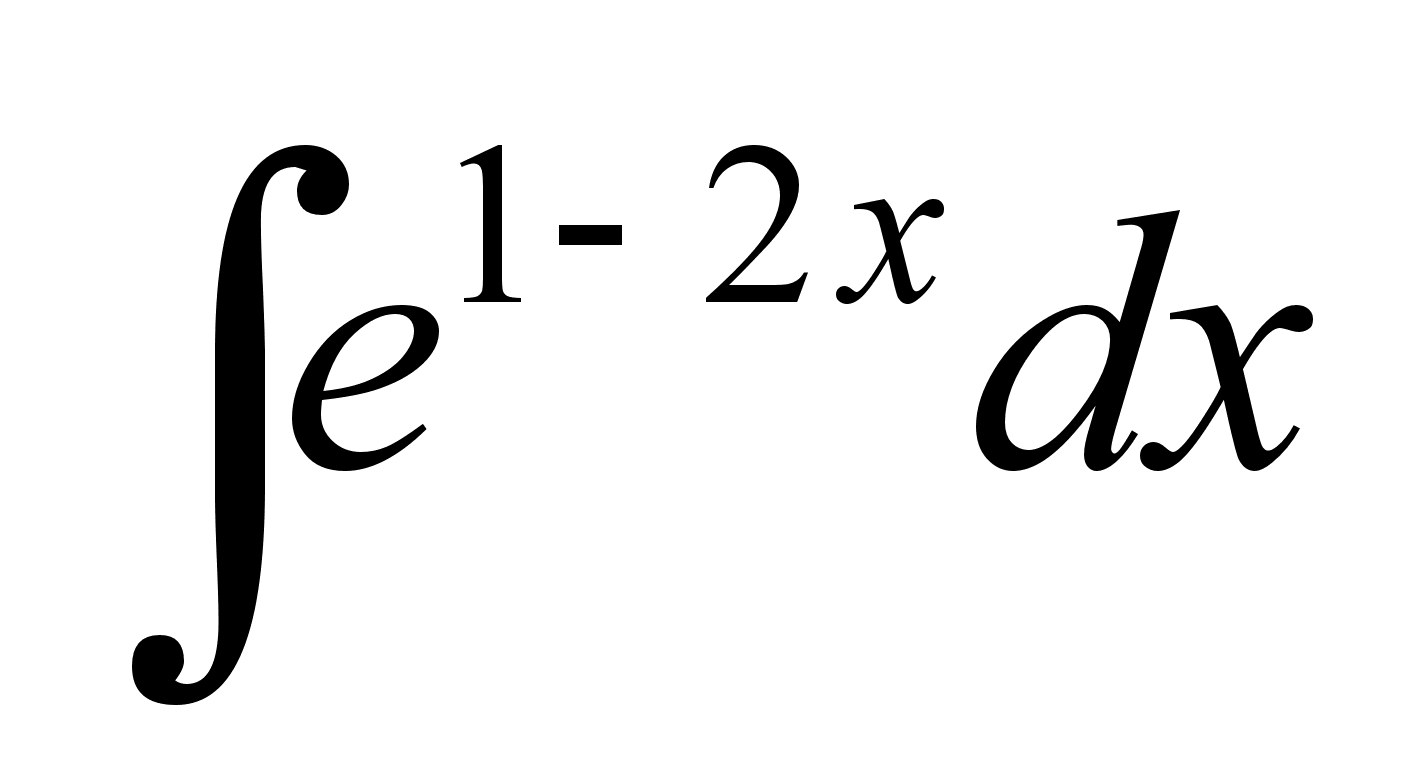 .
.Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего равна: для первого станка 0,9, для второго 0,8, для третьего - 0,85. Какова вероятность того , что в течение некоторого часа, по крайней мере, один станок потребует внимания?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 12
Полярная система координат на плоскости. Связь координат точки в полярной и прямоугольной системах координат.
Правила дифференцирования суммы, разности, произведения и частного двух функций. Привести пример.
Известно, что высказывания a, – истинны, а с – ложно. Определить истинность высказывания (a

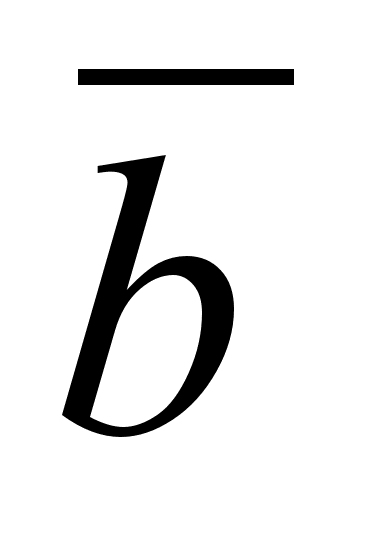 ) c.
) c.Найти общее уравнение медианы треугольника АВС из точки А, если известно:
А (-1, 2), В (2, 5), С (-6, 1).Вычислить определенный интеграл
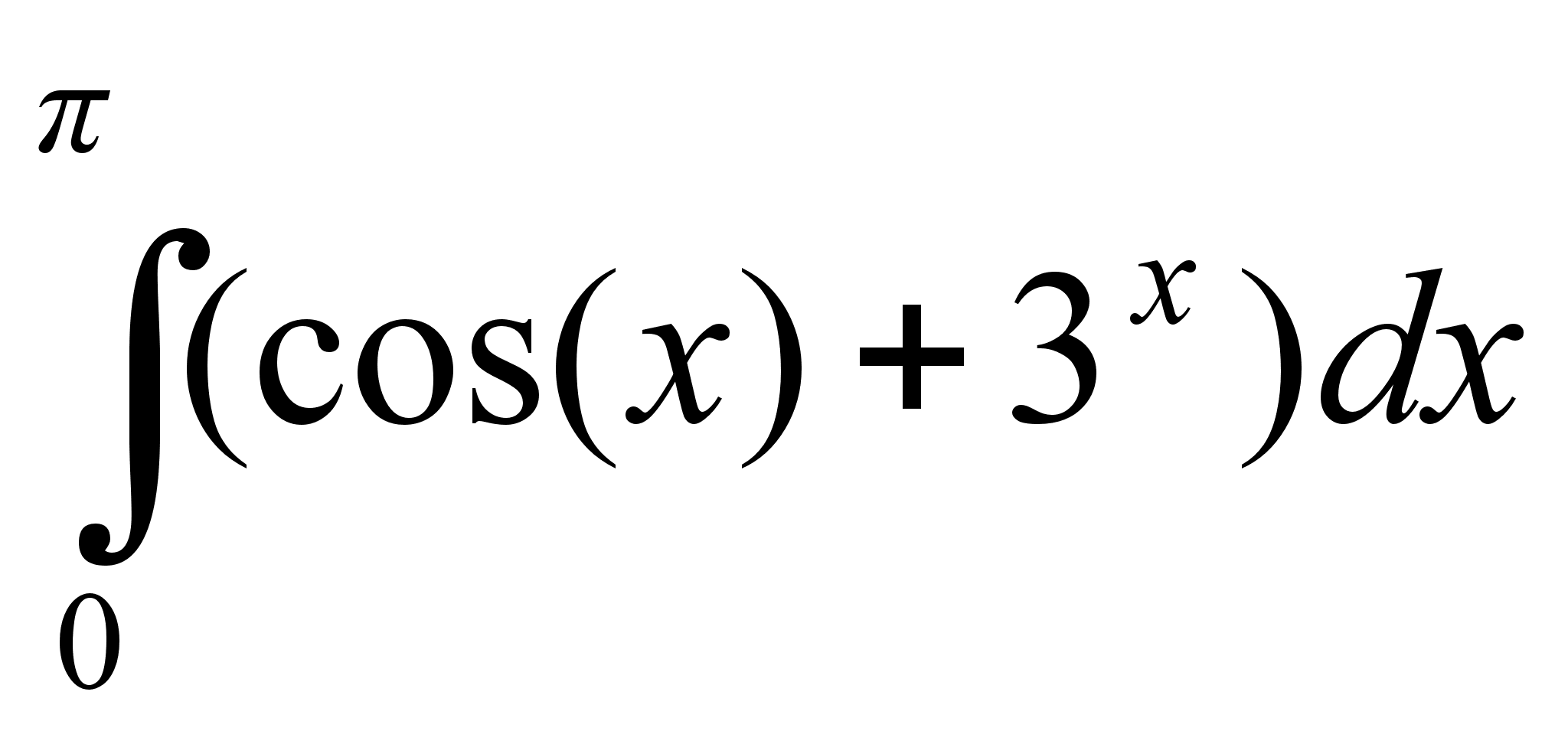 .
.В магазин поступают шариковые ручки с трех фабрик, причем из каждых десяти ручек 3 произведены первой фабрикой, 4 - второй, 3 - третьей. Доля непишущих ручек равна 0.2 в продукции первой фабрики, 0.03 - второй, 0.05 - третьей. Какова вероятность покупки непишущей ручки в магазине?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 13
Дать определение графика числовой функции. Начертить графики функций y= tg (x) и y= arctg (x).
Определение и достаточный признак возрастания функции на интервале. Привести пример.
Определить, какие из точек К (1, -1), L(2, -5), M (-4, -3) принадлежат множеству
А = {(x,y) :x + 1 ≥ y ≥ -x2}.Найти координаты вершин и фокусов гиперболы -9х2 + 16у2 = 144.
Н

айти наклонную асимптоту графика ƒ(х) =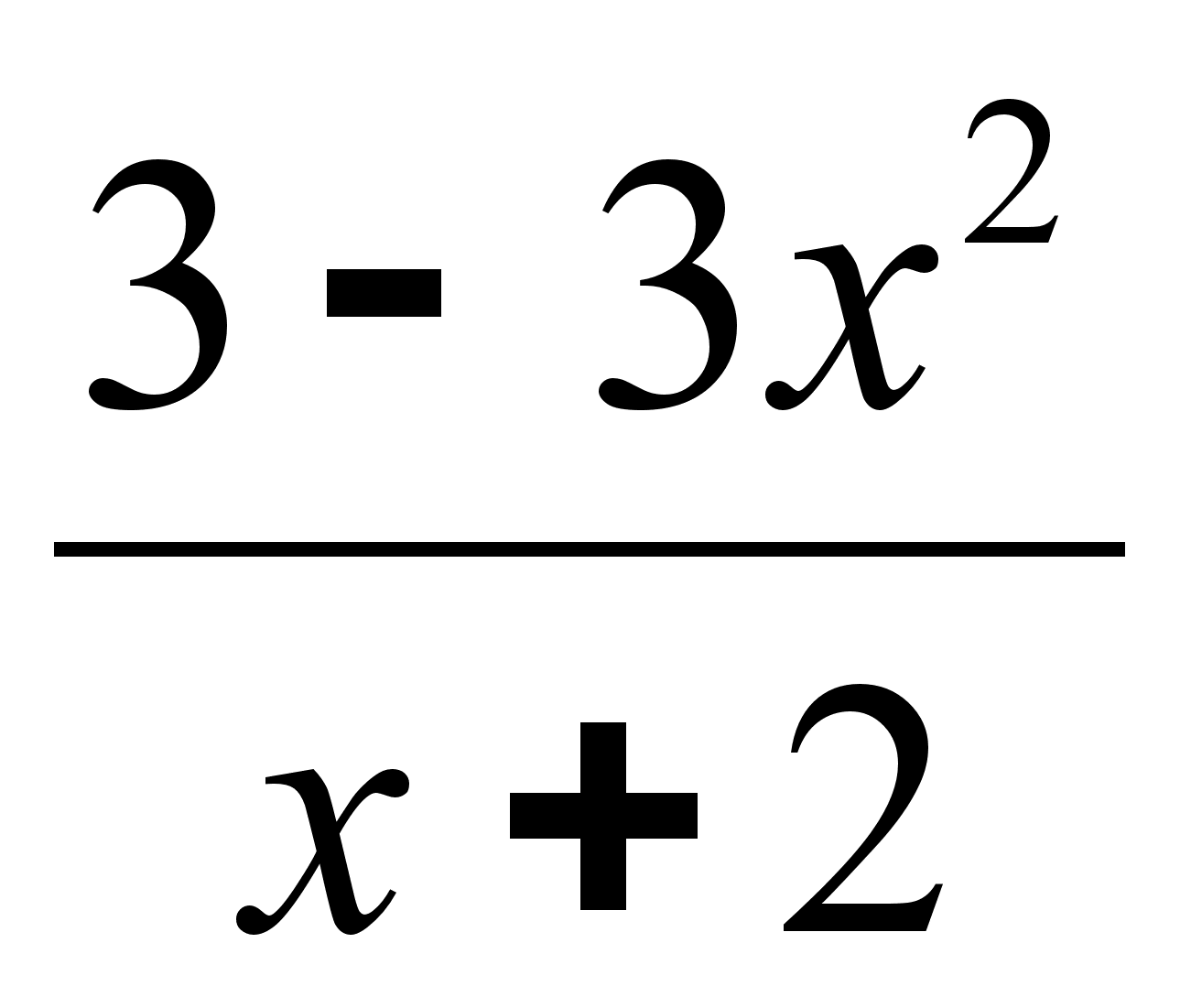 .
.Человеку, достигшему 60-ти лет, вероятность умереть на 61-ом году жизни равна 0,09. Какова вероятность того, что из 4-х человек в возрасте 60-ти лет трое будут живы через год?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 14
Дать определение графика числовой функции. Начертить графики функций
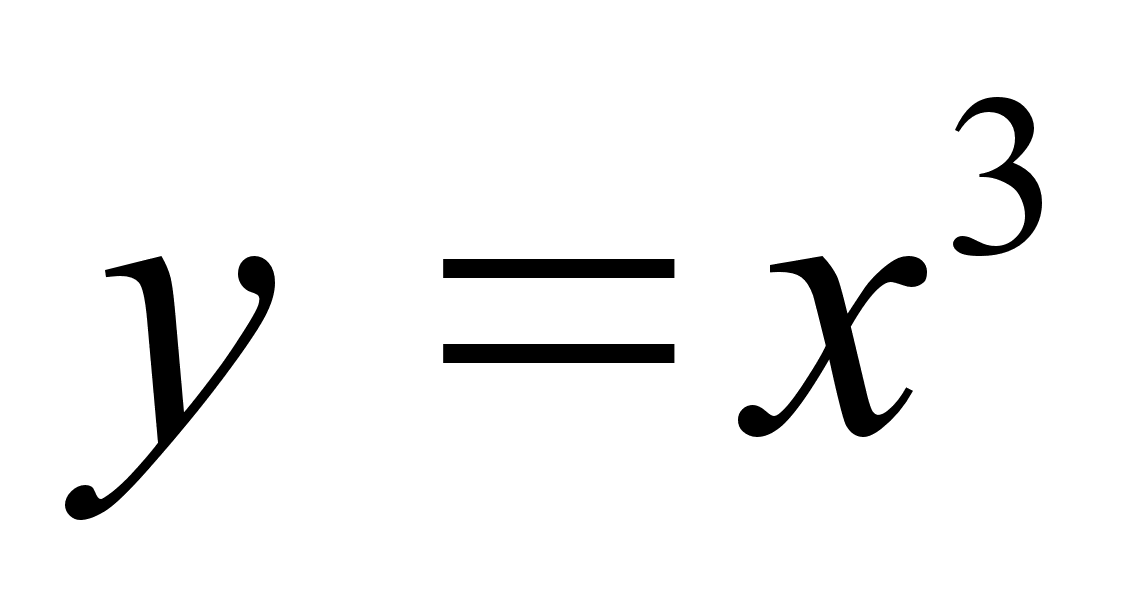 и
и 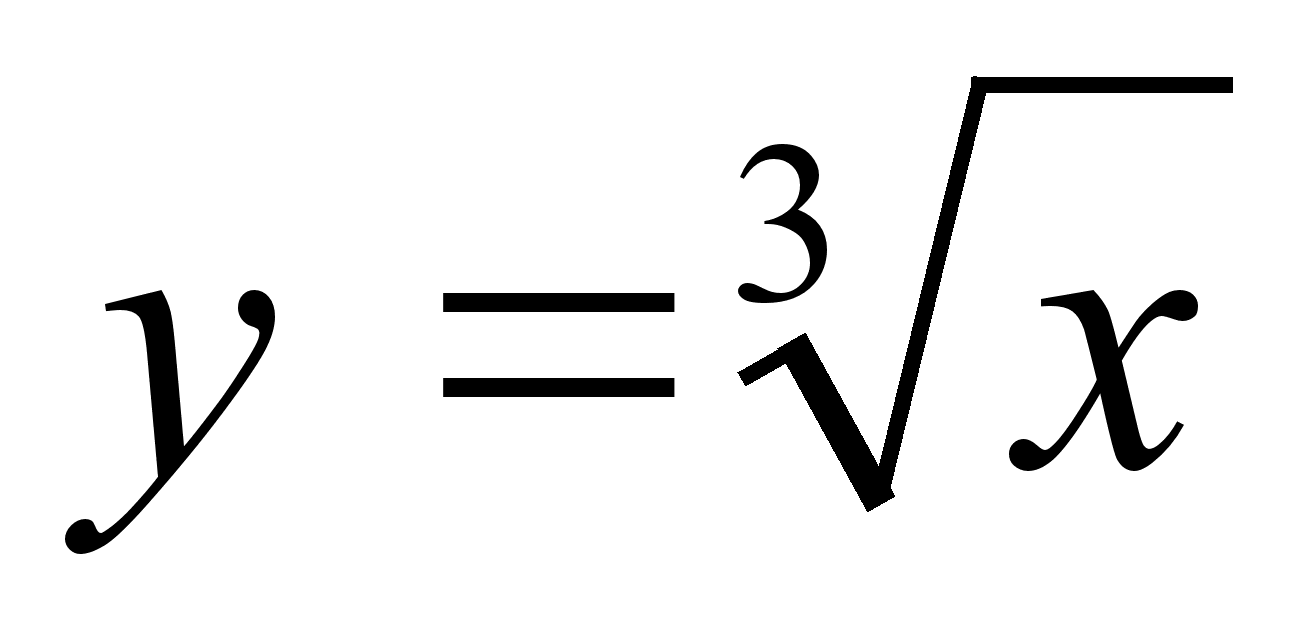 .
.Дать определение условной вероятности. Когда условная вероятность равна нулю?
Найти область определения функции ƒ(х) =
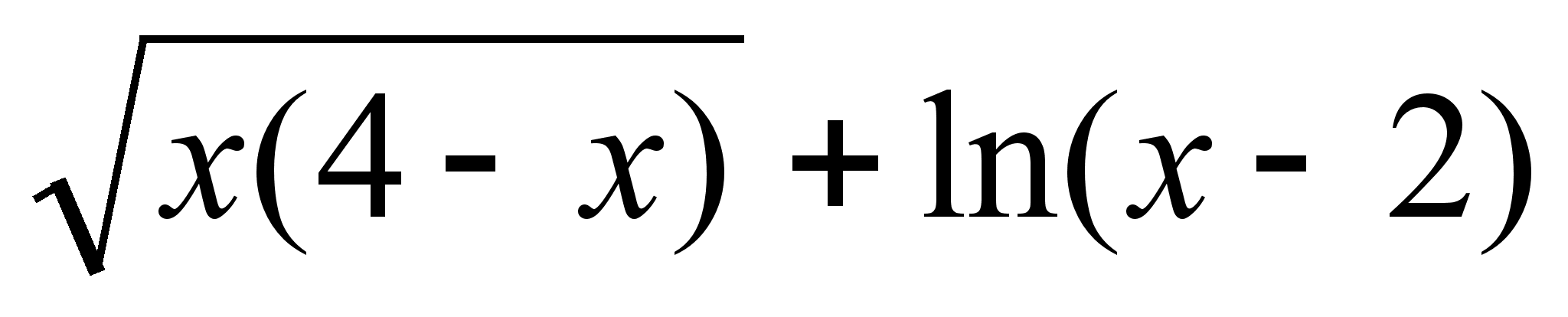 .
.Даны две плоскости 2x - 3y - z + 3 = 0 и -4x + 6y + 2z - 4 = 0.
Будут ли они перпендикулярны или параллельны и почему?Вычислить определенный интеграл
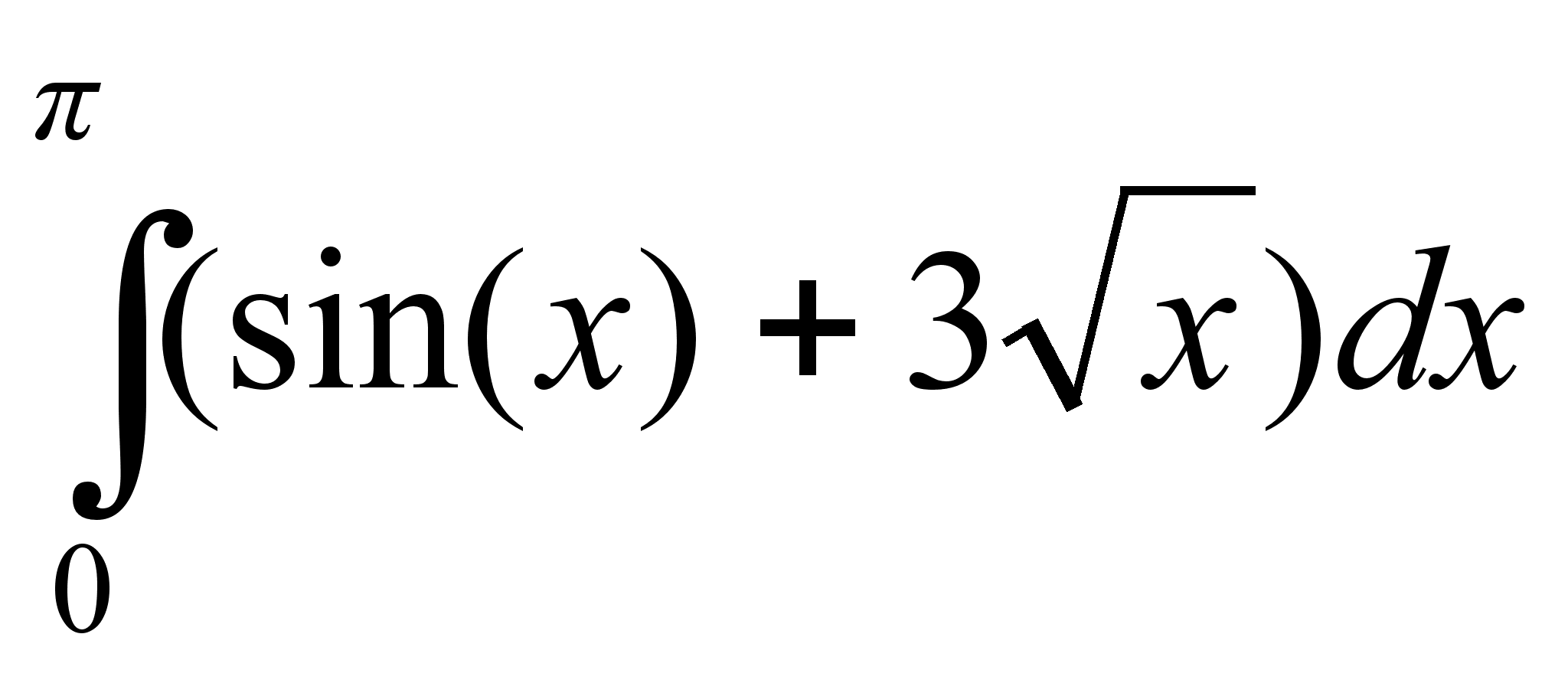 .
.Интервалы между поездами метро 5 минут. Какова вероятность того, что, спустившись в метро в случайный момент времени, придется ждать поезда не меньше 1 минуты и не больше 3 минут? Больше 3 минут?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 15
Дать геометрическое определение эллипса. Что такое фокусы, вершины, центр? Нарисовать чертеж эллипса и показать на нем вышеупомянутые точки.
Определение и достаточный признак убывания функции на интервале. Привести пример.
В результате опроса 100 жителей г. Москвы выяснилось, что 57 человек имеют автомобиль, 48 – дачу, 23- ни того, ни другого. Сколько человек имеют и машину и дачу?
Найти длину вектора
 – 2
– 2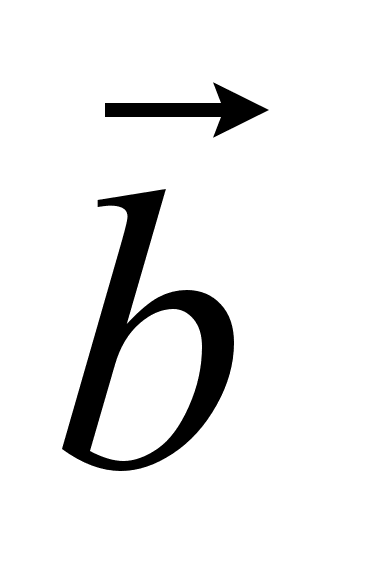 , если дано:
, если дано:  {-2, 5, 3},
{-2, 5, 3}, 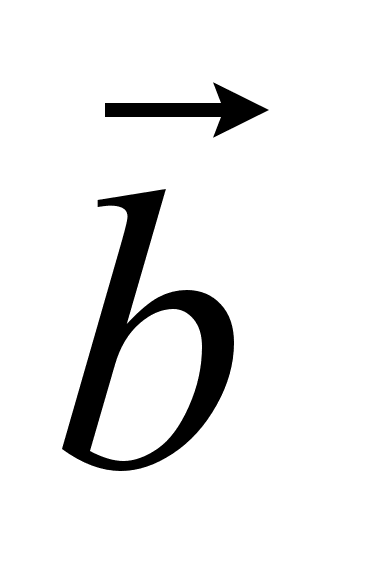 {-5, 7, 7}.
{-5, 7, 7}.Вычислить определенный интеграл
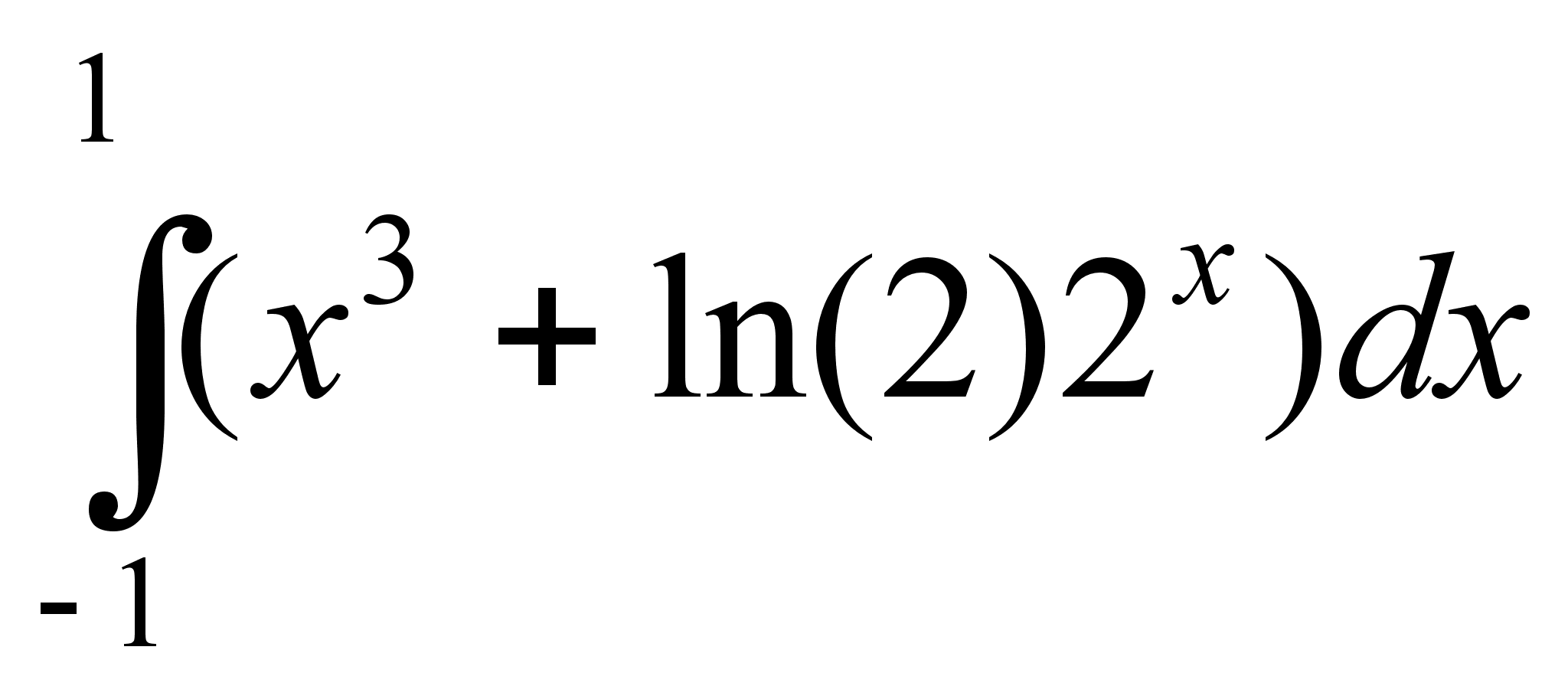 .
.Интервалы между поездами метро 5 минут. Какова вероятность того, что, спустившись в метро в случайный момент времени, придется ждать поезда больше 3 минут? Меньше 2 минут?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 16
Дать определение высказывания и неопределенного высказывания. Привести пример неопределенного высказывания и найти его область истинности.
Что такое схема Бернулли? Записать формулу Бернулли и объяснить, при каких условиях она применяется.
Определить, какие из точек К (0,1), L(-1,1), M (-4, 1) принадлежат множеству
А = {(x,y) :x2 + 1 ≥ y ≥ -x}.Найти косинус угла между векторами
 и
и 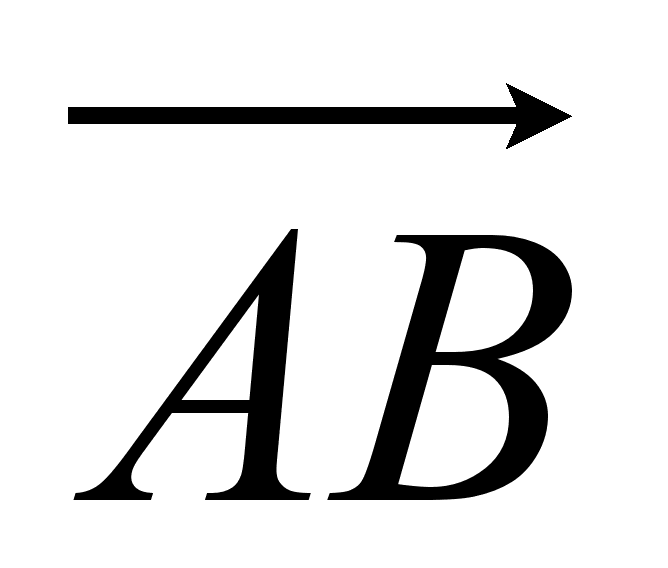 , если известно:
, если известно:  {1, -2, 2}, А (4, -1, 2), В (3, 0, 1).
{1, -2, 2}, А (4, -1, 2), В (3, 0, 1).Вычислить неопределенный интеграл
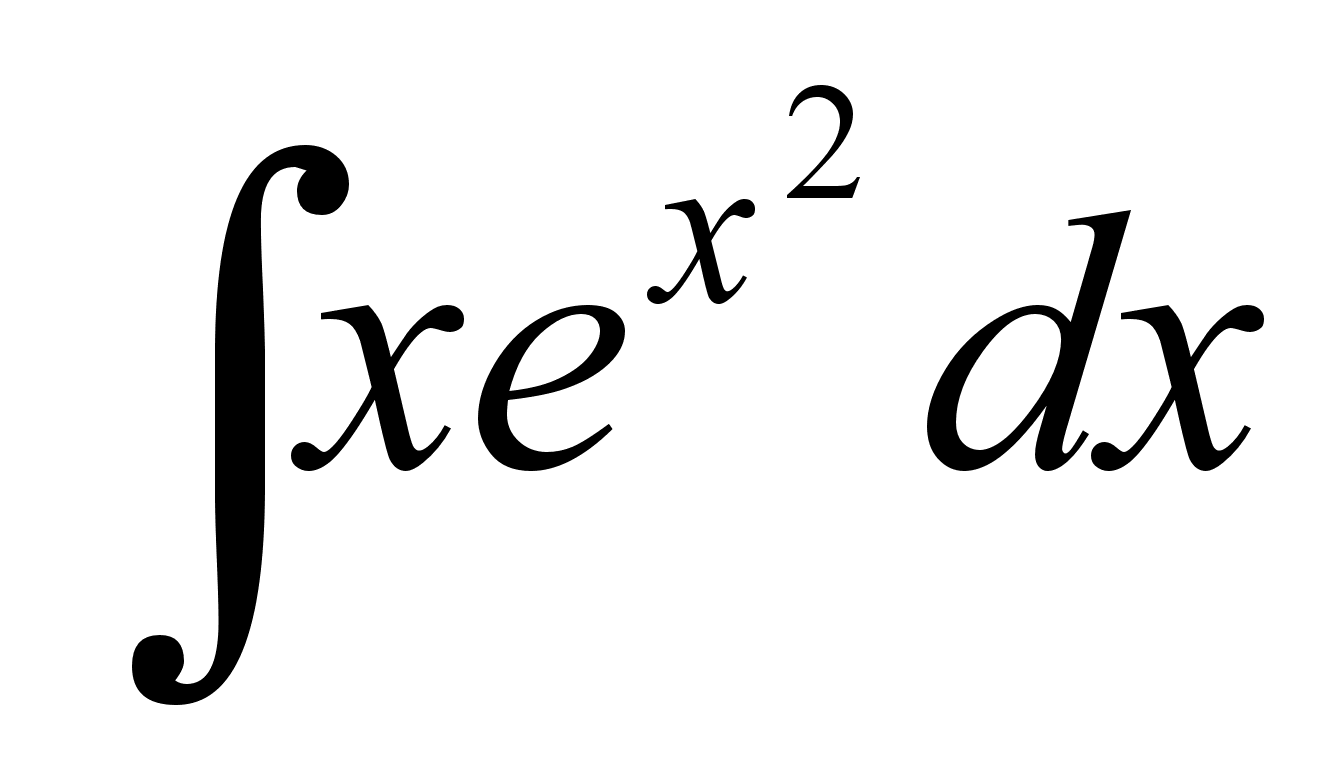 .
.Брошены две игральные кости. Найти вероятность того, что произведение выпавших очков окажется равным 12, меньше 12.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 17
Дать определение области определения и области значений числовой функции. Описать области определения и значений функции y = sin(x).
Сформулировать первый и второй замечательный пределы.
Построить диаграмму Венна и проверить истинность следующего рассуждения: некоторые а являются и все являются с, следовательно, некоторые а являются с.
Написать уравнение плоскости, проходящей через точку (4, 2, 1) перпендикулярно прямой
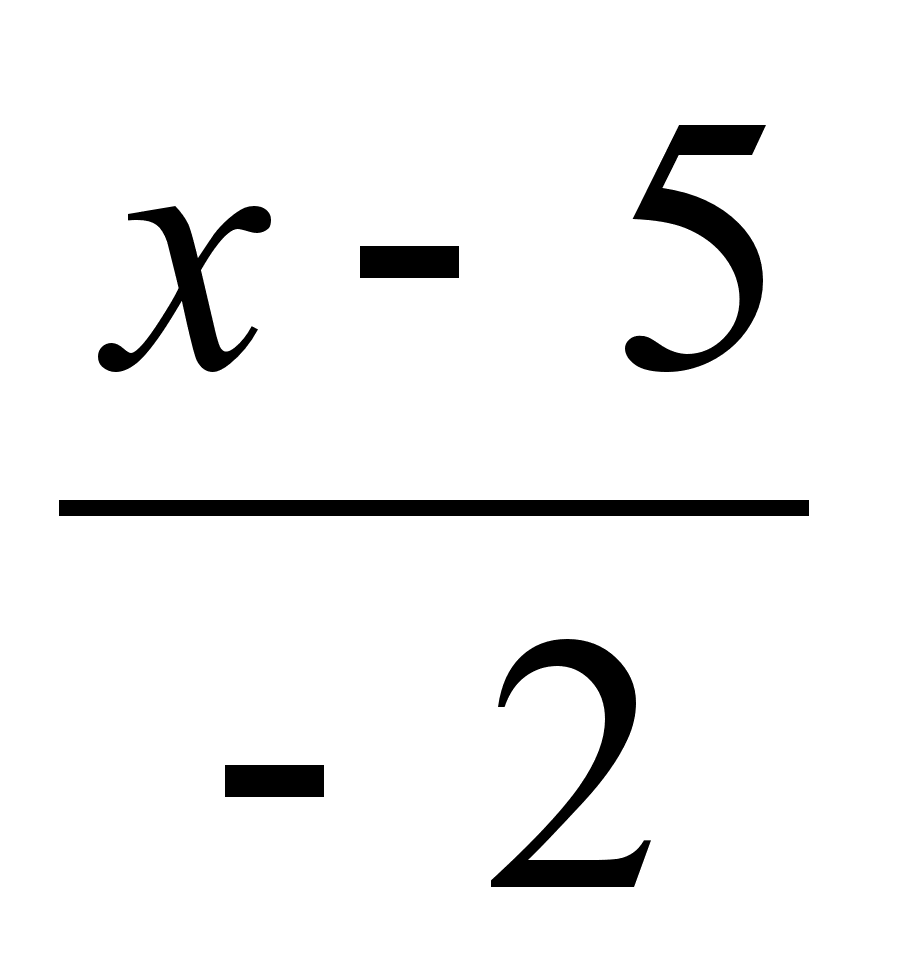 =
= 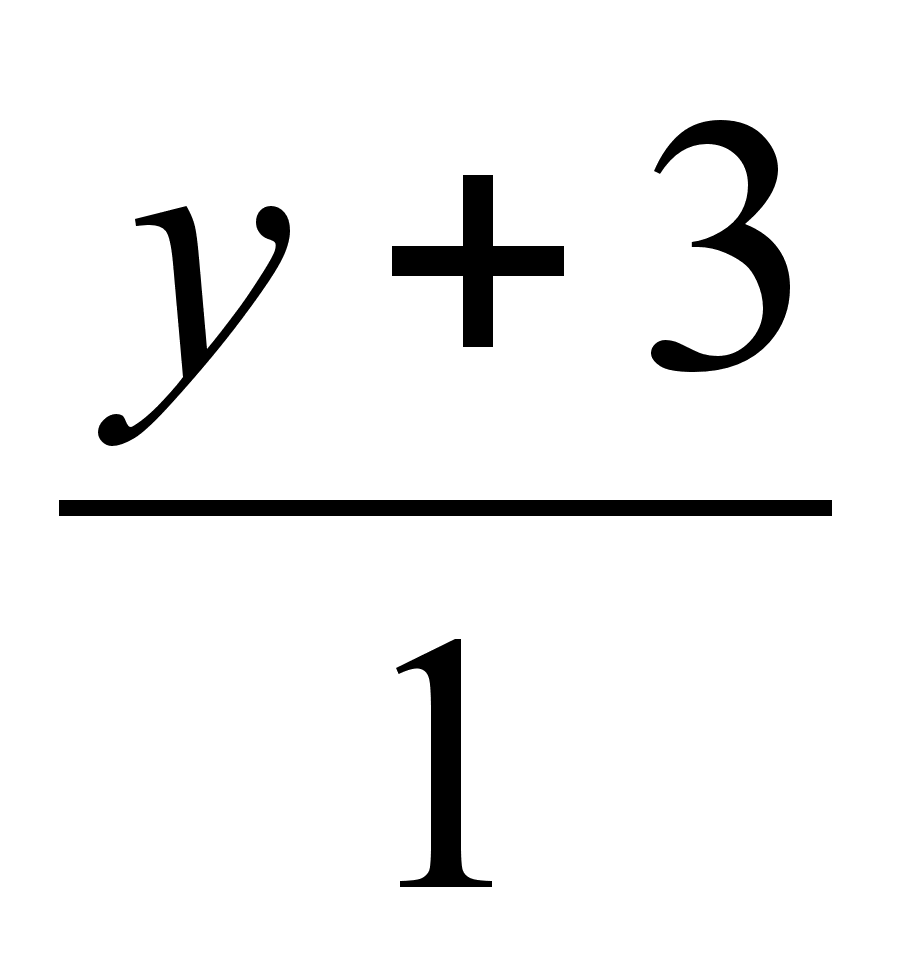 =
= 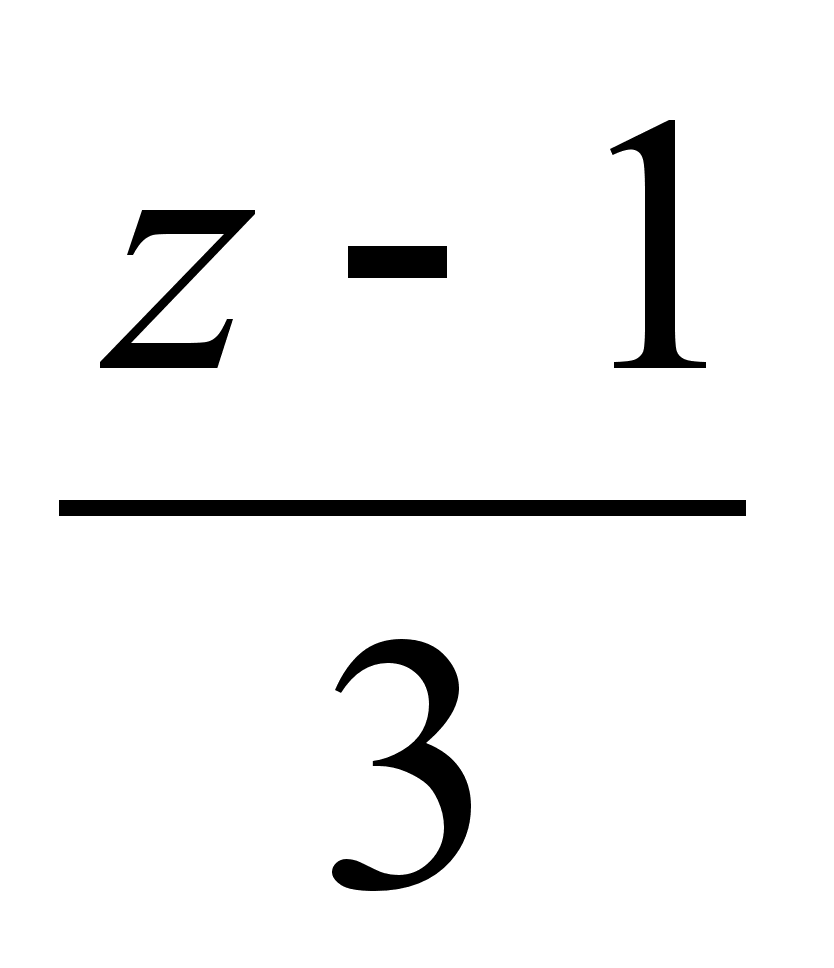 .
.Найти наклонную асимптоту графика ƒ(х) =
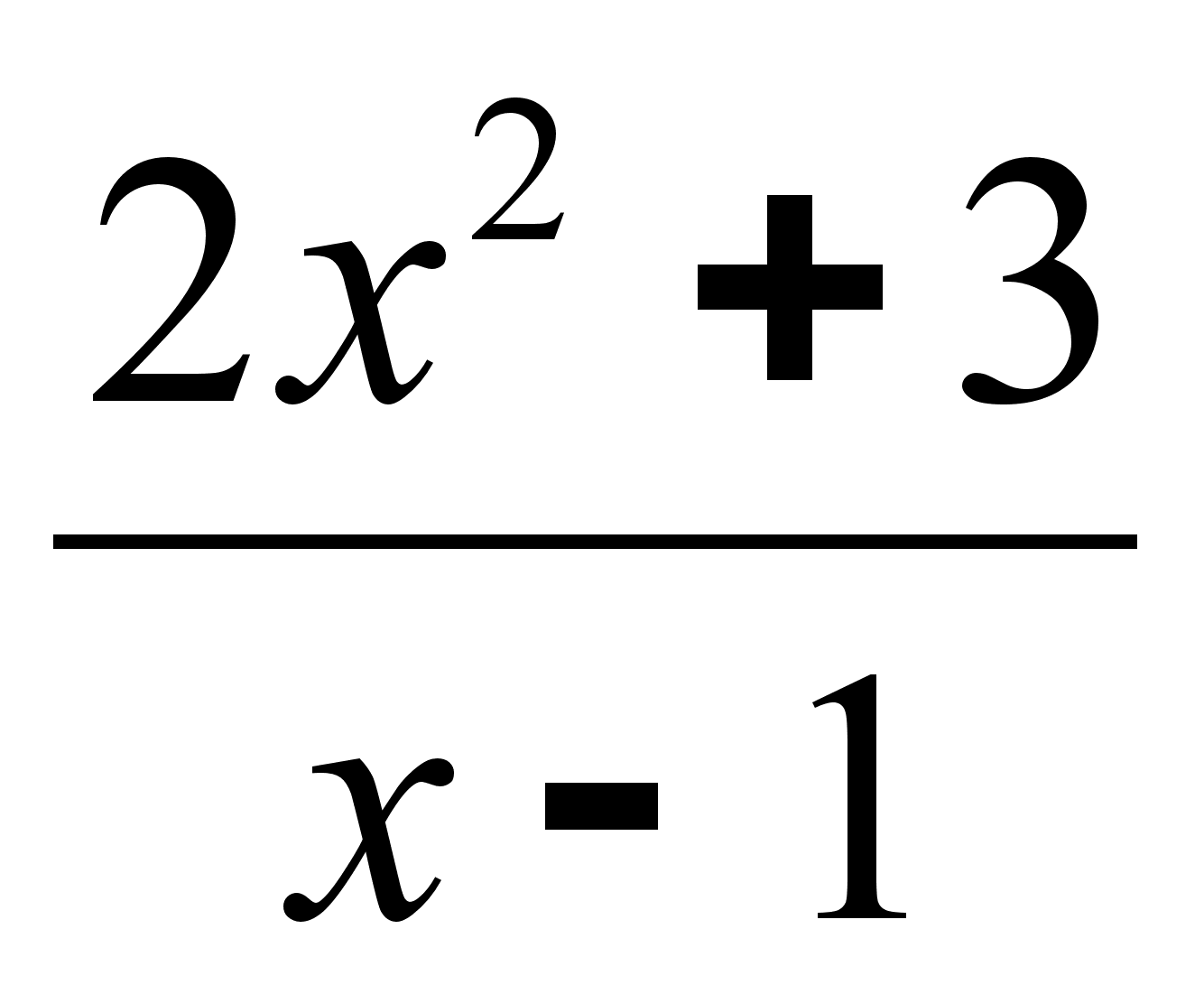 .
.В кучу сложены яблоки с трех яблонь. Урожай первой яблони составляет 50 кг, второй - 40 кг, третьей - 30 кг. Доля червивых яблок составляет 0.3 для первой яблони, 0.2 - для второй, 0.4 - для третьей. Найти вероятность того, что случайным образом взятое яблоко из кучи окажется червивым.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 18
Каноническое уравнение параболы. Геометрический смысл его параметра. Формула координат фокуса и уравнения директрисы. Привести пример.
В чем заключается правило «трех сигм»? Как оно может применяться на практике?
Найти область определения функции ƒ(х) =
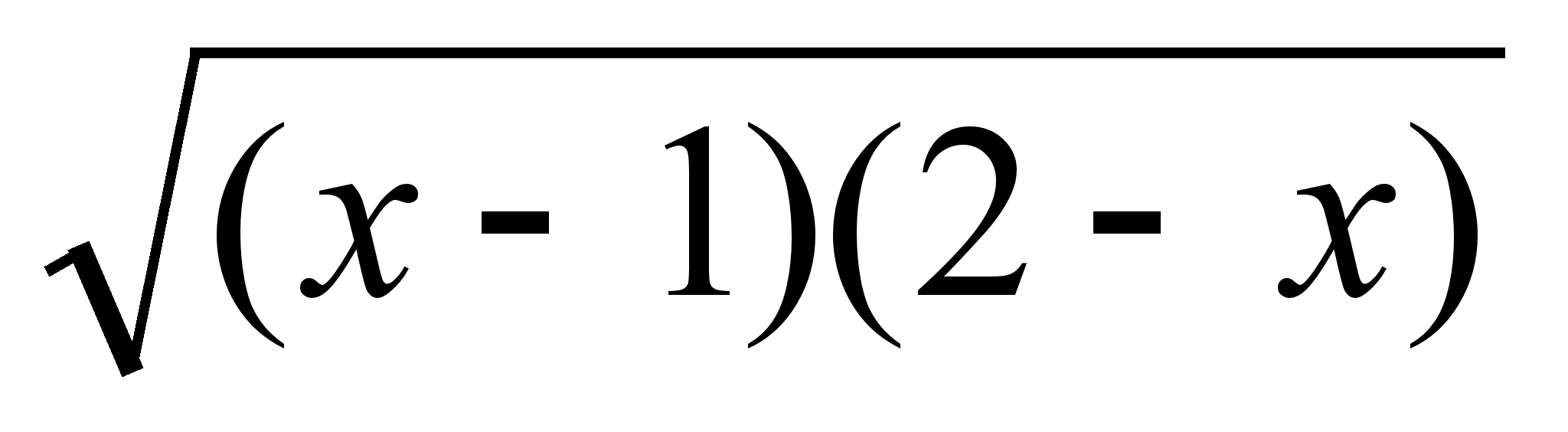 +
+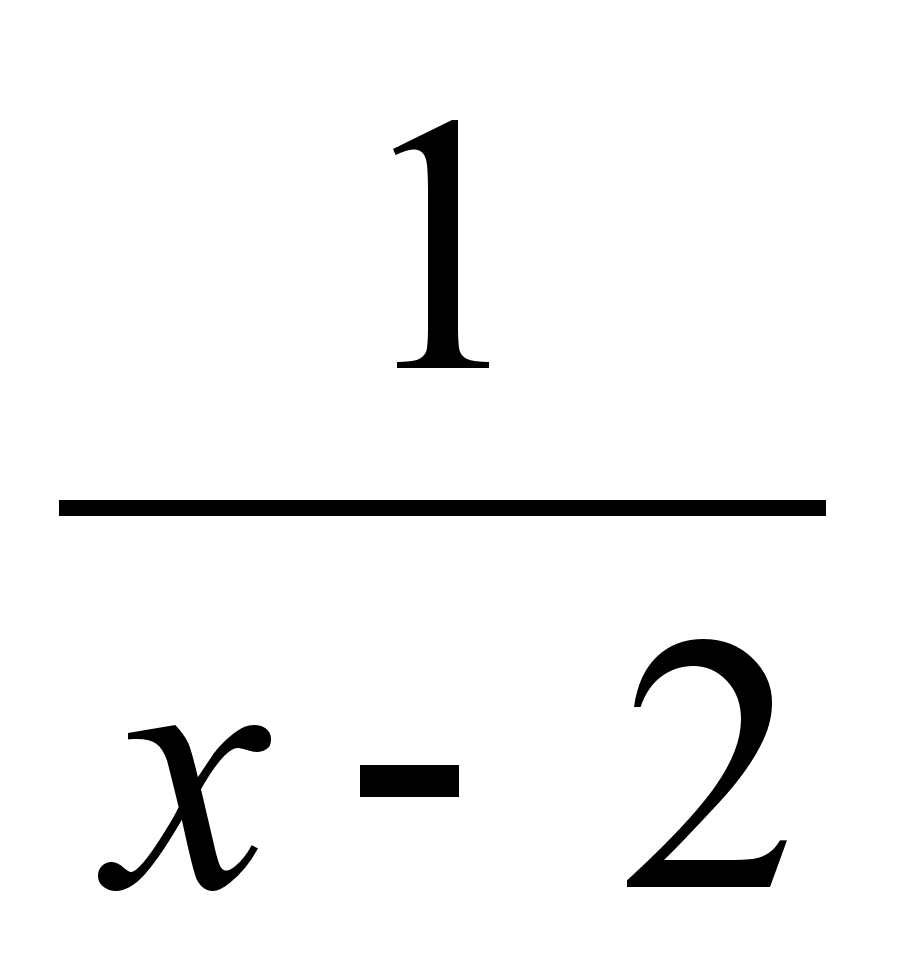 .
.Найти координаты вершин и фокусов эллипса 16х2 + 9у2 = 144.
Найти наклонную асимптоту графика ƒ(х) =
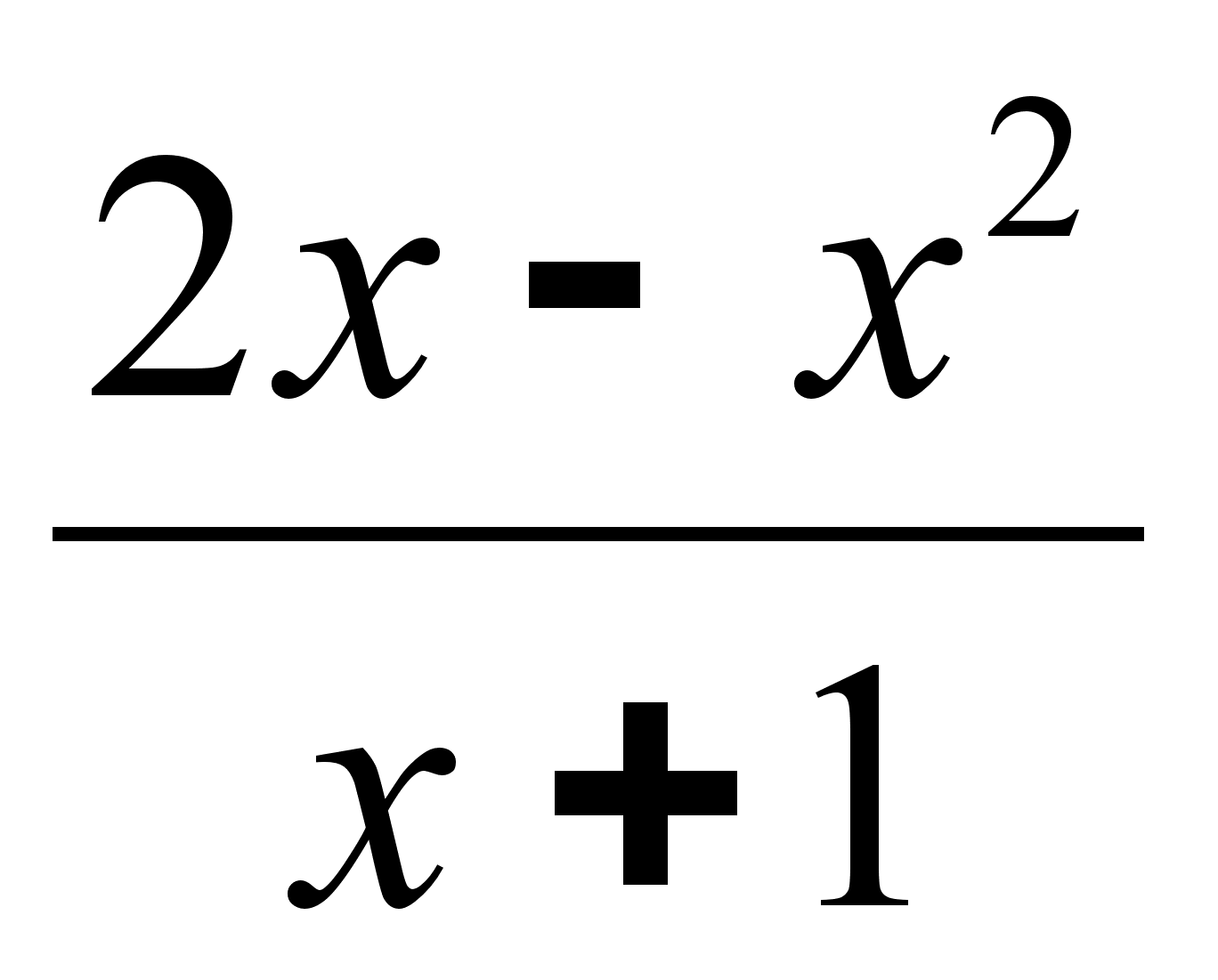 .
.Для нормальной величины X~N(2,4). Найти М(-2x+1), D(-2x+1).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 19
Дать определение взаимно-однозначного соответствия множеств А и В. Привести пример взаимно-однозначного соответствия и пример отображения, которое не является взаимно-однозначным соответствием.
Дать определение суммы двух событий. Записать формулу вероятности суммы двух событий и привести пример ее применения.
Построить диаграмму Венна и проверить истинность следующего рассуждения: некоторые а являются и некоторые являются с, следовательно, некоторые а являются с.
Найти косинус угла между векторами
 и
и 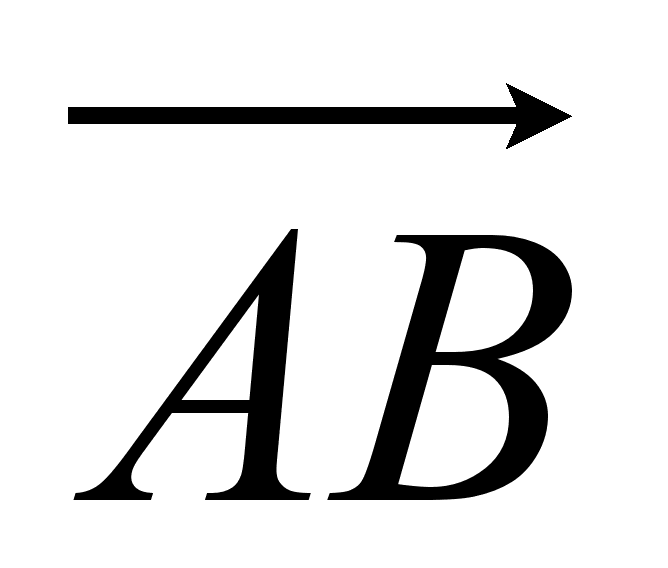 , если известно:
, если известно:  {2, -1, 0}, А (-1, 3, 5), В ( -3, 3, 4).
{2, -1, 0}, А (-1, 3, 5), В ( -3, 3, 4).Вычислить площадь фигуры, ограниченной линиями
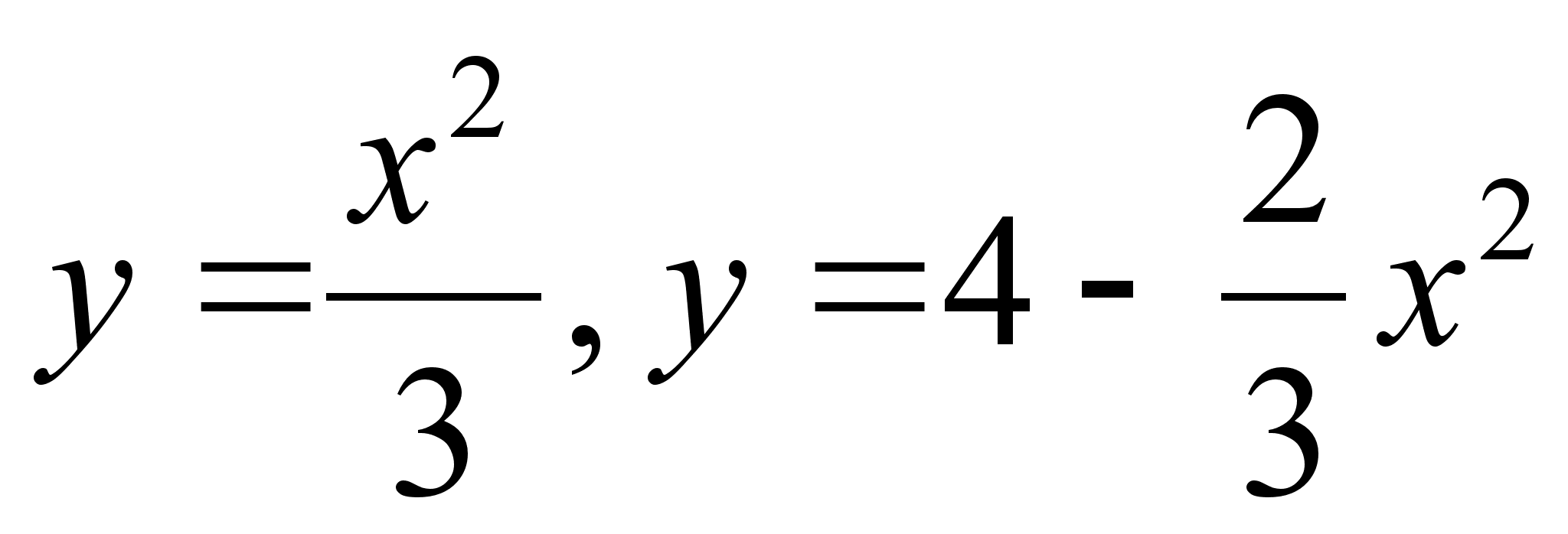 .
.Продавец реализует в среднем 3 автомобиля в день и считает день удачным, если продаст не менее пяти машин. Найти вероятность того, что день окажется неудачным.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 20
Каноническое уравнение эллипса. Геометрический смысл его параметров. Формулы для координат вершин и эксцентриситета. Привести пример.
Как определяется и какими свойствами обладает функция распределения случайной величины? Нарисовать график какой-нибудь функции распределения.
Построить диаграмму Венна и проверить истинность следующего рассуждения: все а являются и некоторые являются с, следовательно, некоторые а являются с.
Найти координаты вершин и фокусов эллипса 9х2 + 36у2 = 324.
Вычислить неопределенный интеграл
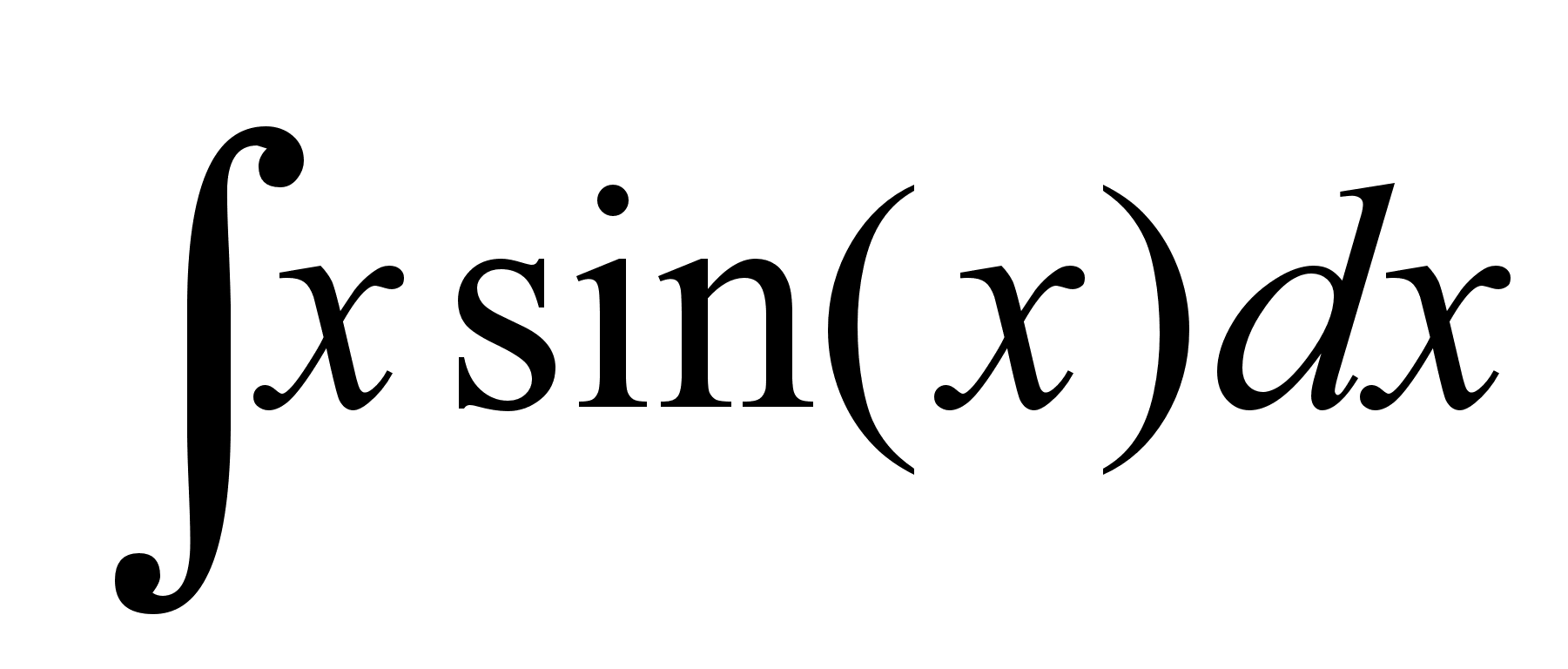 .
.При передаче закодированного сообщения вероятность ошибки одного знака равна 0,02. Найти вероятность того, что сообщение из 150 знаков содержит ошибку.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 21
Каноническое уравнение эллипса. Геометрический смысл его параметров. Формулы координат фокусов. Привести пример.
Алгоритм нахождения интервалов возрастания и убывания функции. Привести пример.
Найти область определения функции ƒ(х) =
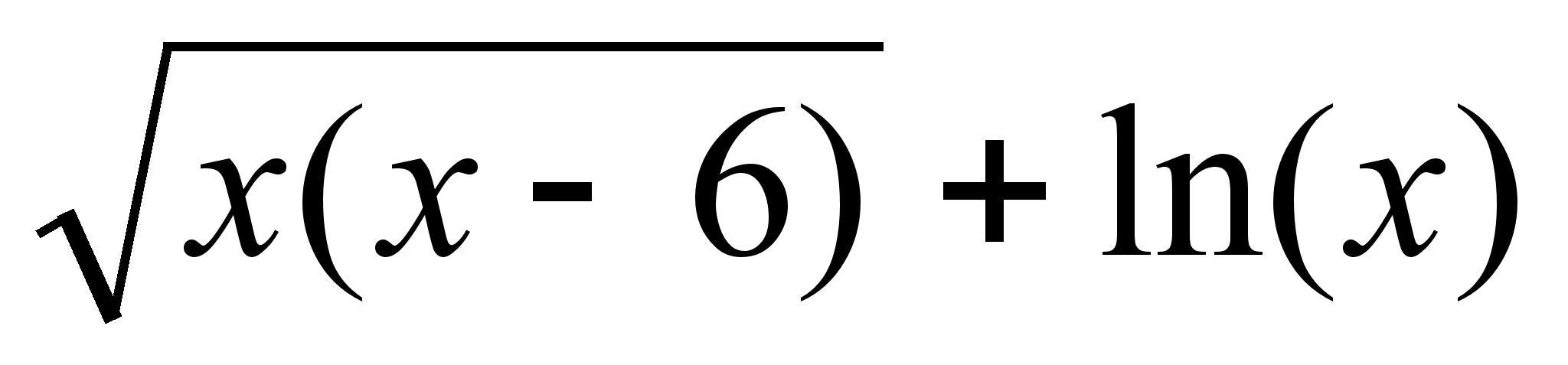 .
.Написать уравнение параболы с вершиной в начале координат и горизонтальной директрисой, причем парабола проходит через точку (-2, 36).
Найти производную функции f(x) =
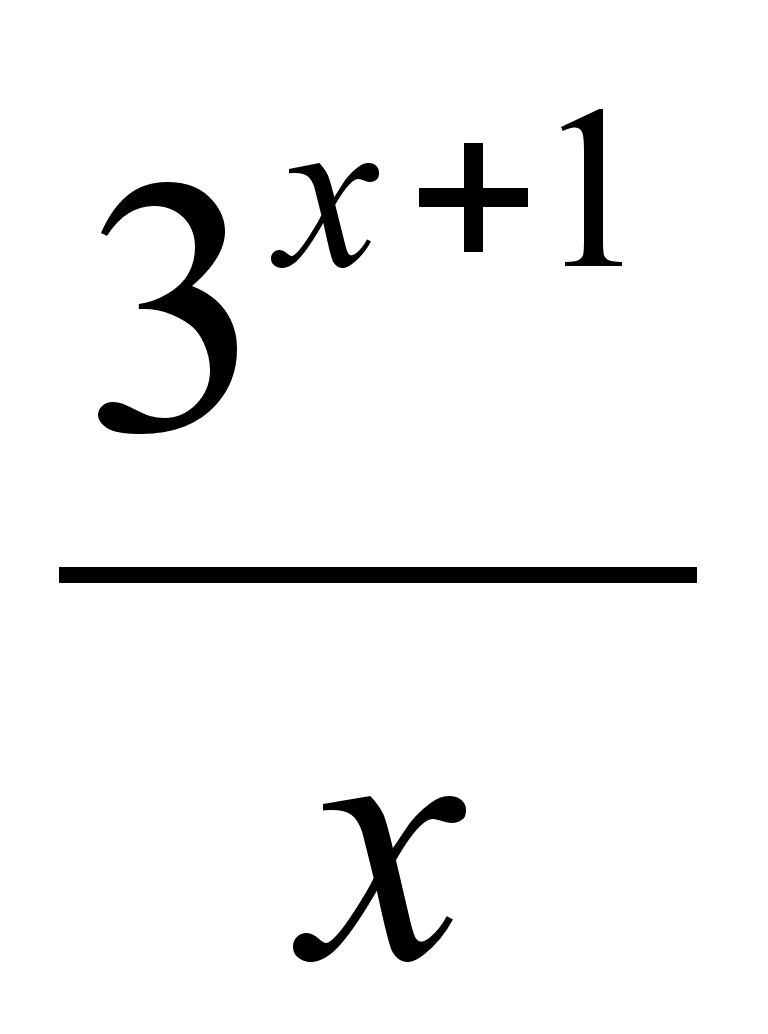 .
.Для независимых нормальных случайных величин X~N(2,1) и Y~N(4,3). найти
М(x+y), М(x-y) и D(x+y), D(x-y).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 22
Дать определение области определения и области значений числовой функции. Описать области определения и значений функции y = x2 .
Алгоритм нахождения точек перегиба, участков выпуклости и вогнутости графика функции.
В первую сессию торгов акции компании подешевели на 30%, во вторую подешевели на 10% к первой. На сколько процентов изменилась цена акции за 2 сессии?
Найти общее уравнение медианы треугольника АВС из точки А, если известно:
А (3, -1), В (-3, 1), С (-1, 1).Найти производную функции f(x) =
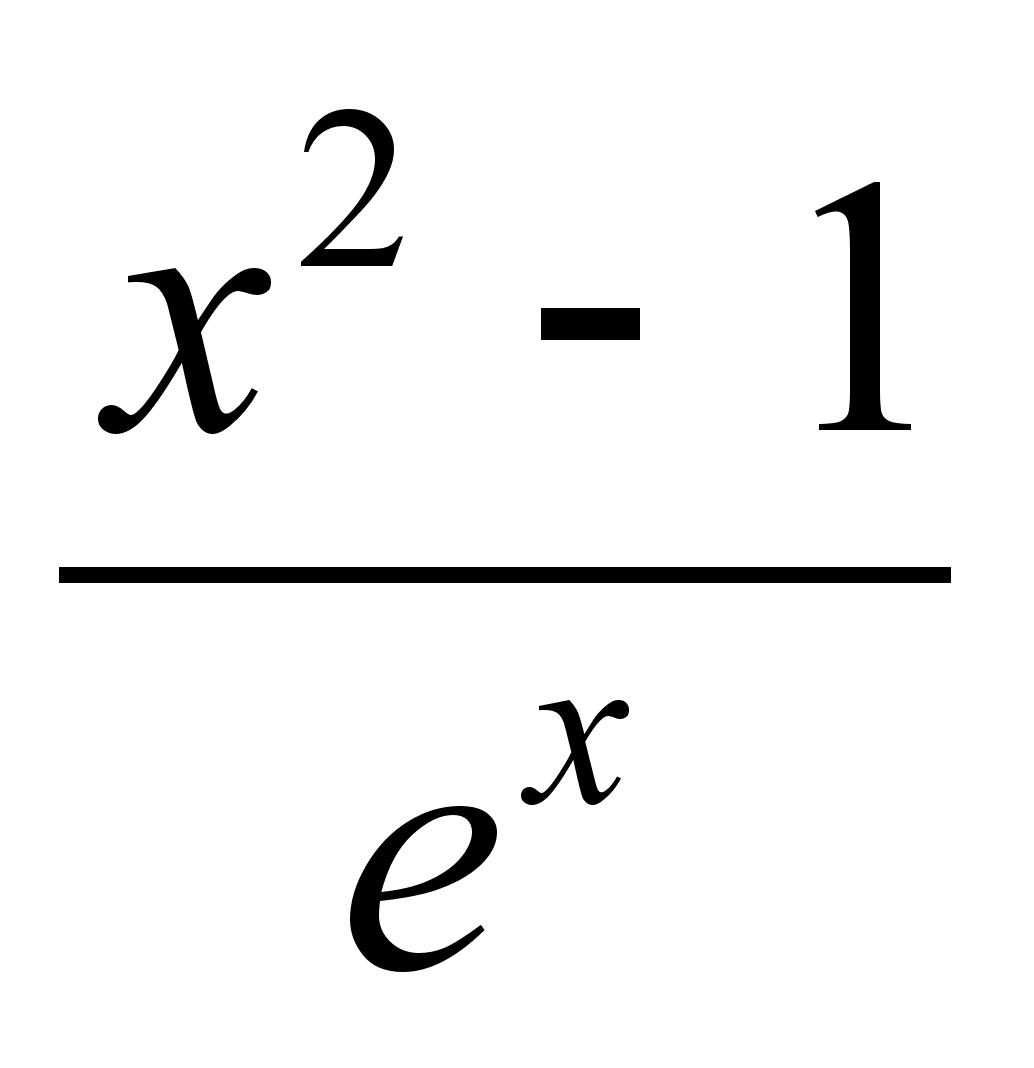 .
.Из трех орудий произведен залп по мишени. Вероятность попадания из первого орудия 0,8, из второго - 0,6, из третьего - 0,5. Какова вероятность поражения цели?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 23
Какие множества называются счетными? Привести пример счетного множества, и проверить, что оно счетно, исходя из определения.
Записать формулу полной вероятности и привести пример ее применения.
Разность арифметической прогрессии равна –1, а сумма первых 7 равна 0. Найти сумму первых 8 членов.
Написать уравнение параболы с вершиной в начале координат и горизонтальной директрисой, причем парабола проходит через точку (3, -54).
Вычислить определенный интеграл

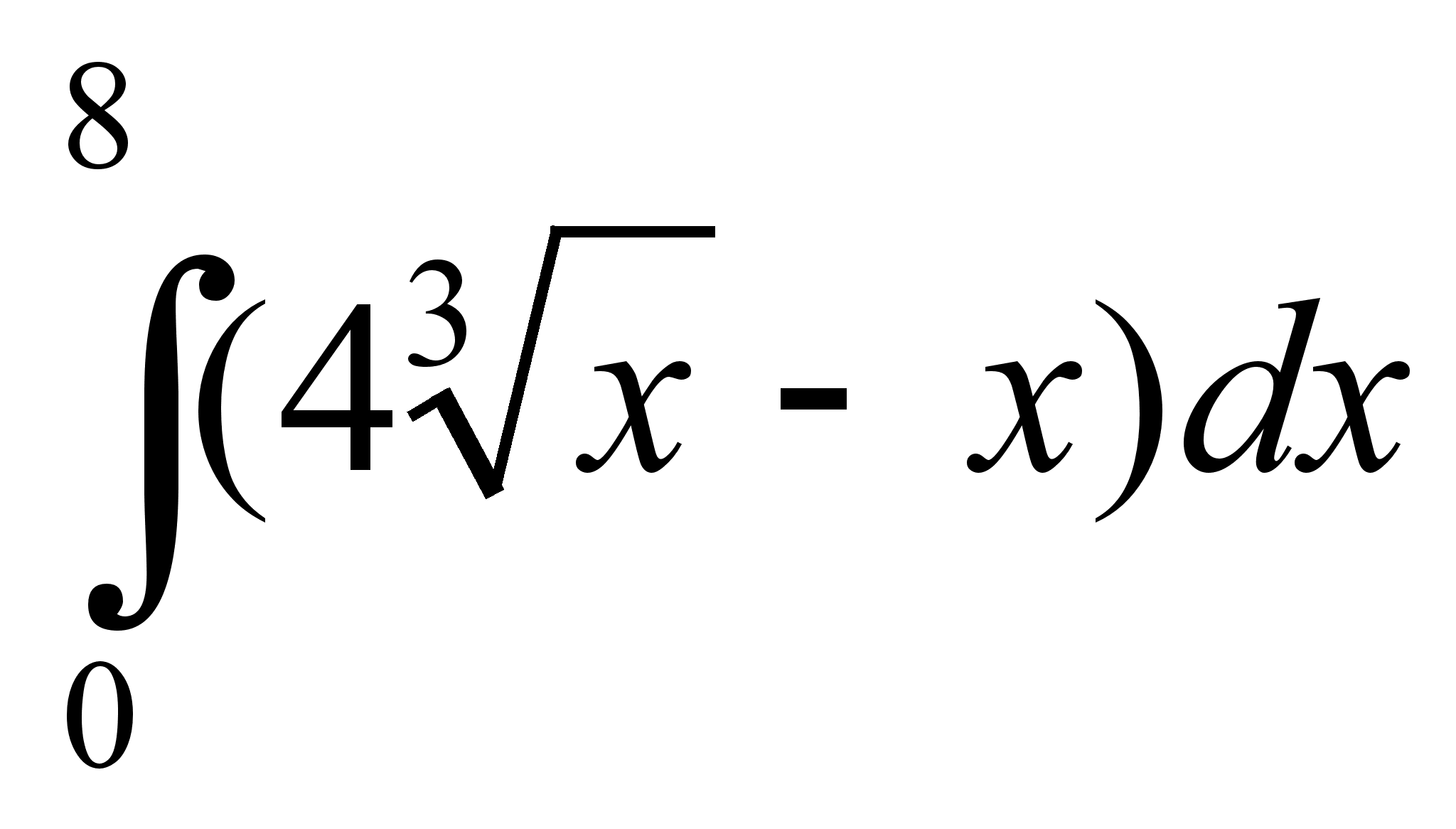 .
.Для независимых нормальных случайных величин X~N(4,3) и Y~N(5,4). найти
М(x+y), М(x-y) и D(x+y), D(x-y).
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 24
Дать геометрическое определение параболы. Что такое вершина, директриса, фокус? Нарисовать чертеж параболы и показать на нем вышеупомянутые точки и прямую.
Правило интегрирования по частям неопределенного интеграла. Привести пример.
Магазин продал в первый день 50% товара, а во второй – 40% остатка. Сколько процентов товара осталось непроданным?
Дано уравнение кривой в декартовых координатах: 5х2+ 5у2 = -3х. Написать это уравнение в полярных координатах.
Вычислить площадь фигуры, ограниченной линиями
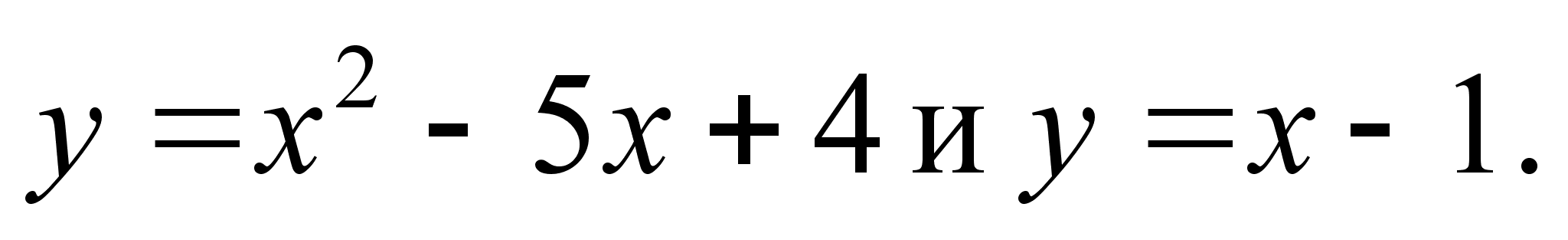 .
.В магазин приходит в среднем 300 клиентов в час. Найти вероятность того, что в данную минуту зайдет ровно 1 клиент.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 25
Угол между плоскостями в пространстве. Формула косинуса угла. Привести пример применения этой формулы.
Как формулируется геометрическое определение вероятности?
Опрос 100 выпускников школ показал, что 41 из них руководствуются мнением родителей, 58 – мнением сверстников, а 21 – обоими. Сколько выпускников руководствуется лишь собственным мнением?
Найти координаты вершин и фокусов гиперболы 4х2 - 16у2 = 64.
Вычислить неопределенный интеграл
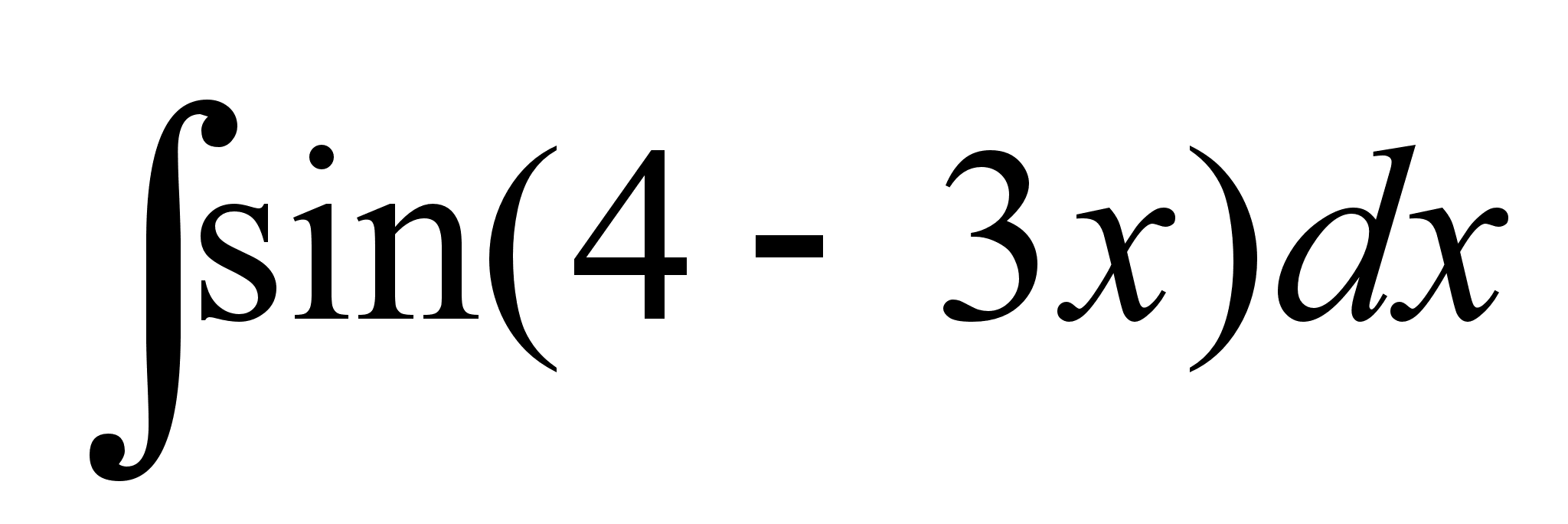 .
.Плотность распределения случайной величины Y такова: f(x)=0 при х <1 и х > 6, f(x)) =
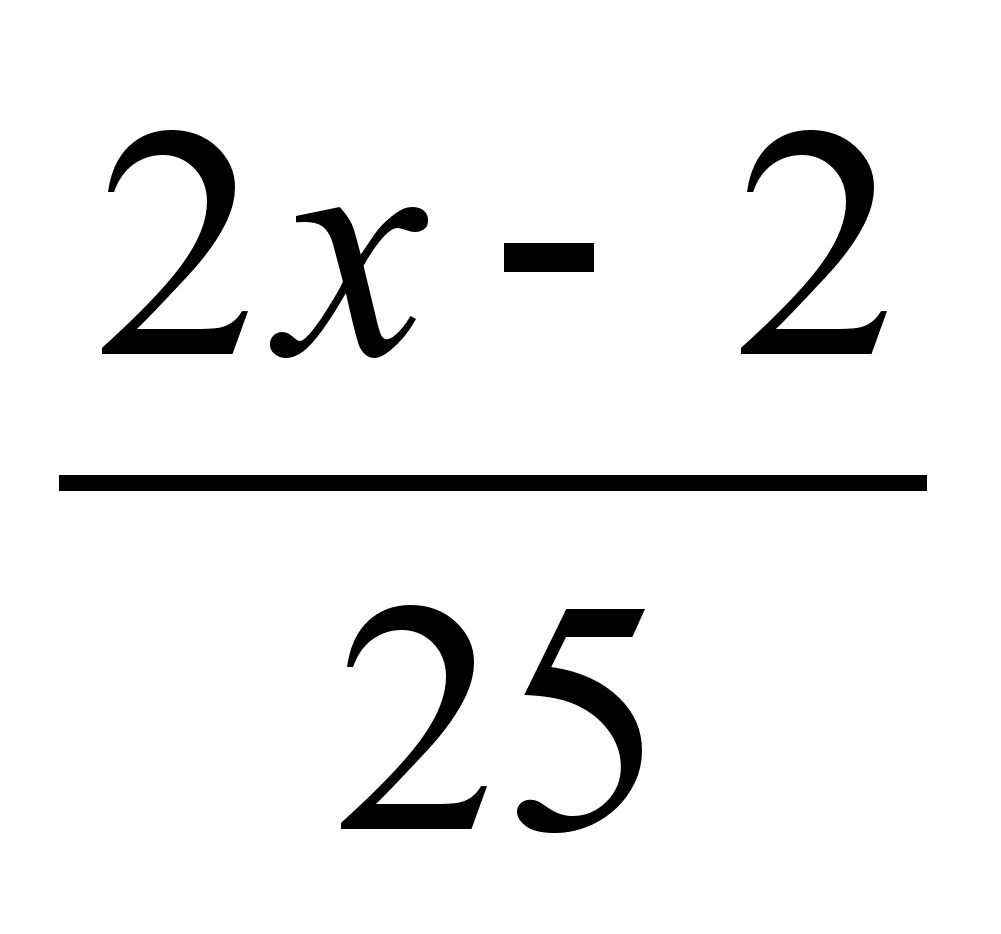 при х∈ (1,6). Найти вероятность того, что случайная величина Y больше 4.
при х∈ (1,6). Найти вероятность того, что случайная величина Y больше 4.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 26
Дать определение импликации высказываний. Построить две возможные импликации высказываний «целое число х делится на 3» и «целое число х делится на 6». Являются ли импликации истинными?
Алгоритм нахождения максимума и минимума функции на отрезке.
В первую сессию торгов акции компании подешевели на 10%, во вторую подорожали на 20% к первой. На сколько процентов изменилась цена акции за 2 сессии?
Написать уравнение плоскости, проходящей через точку (0,-1, 4) перпендикулярно прямой
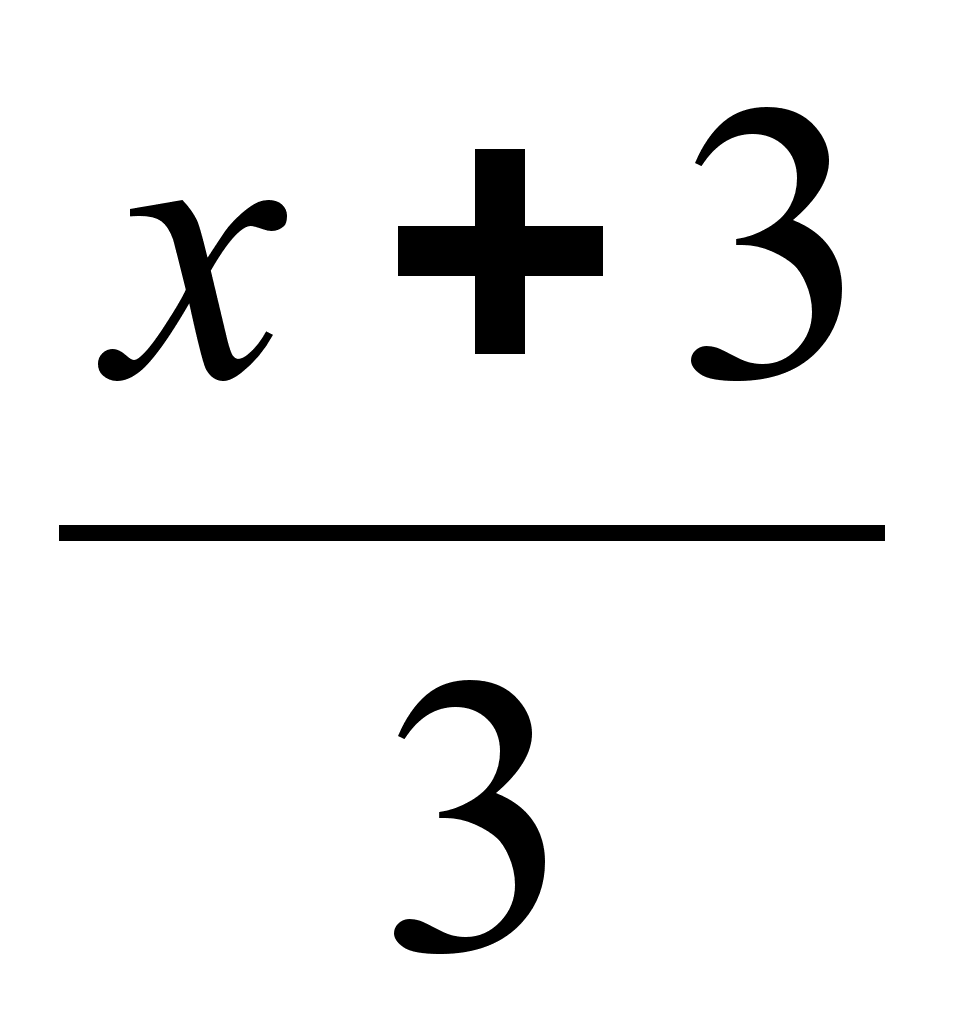 =
= 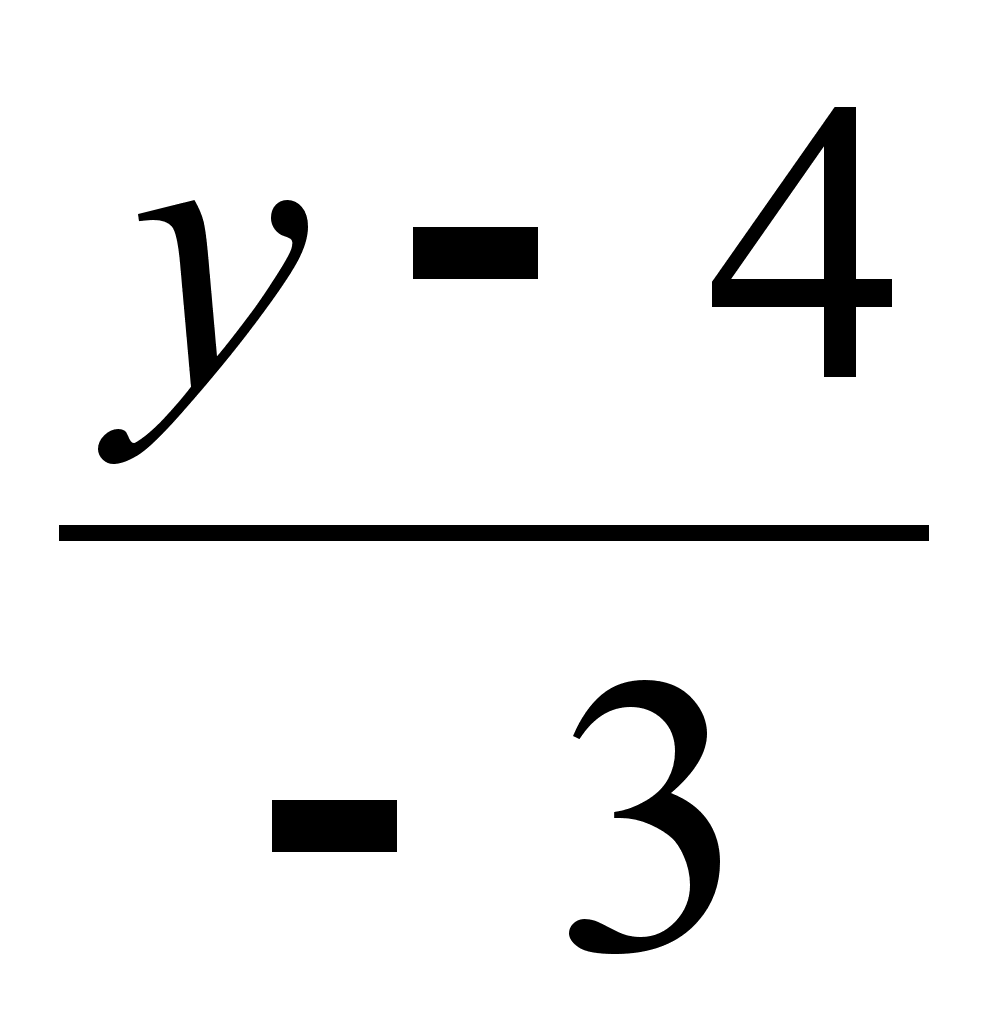 =
= 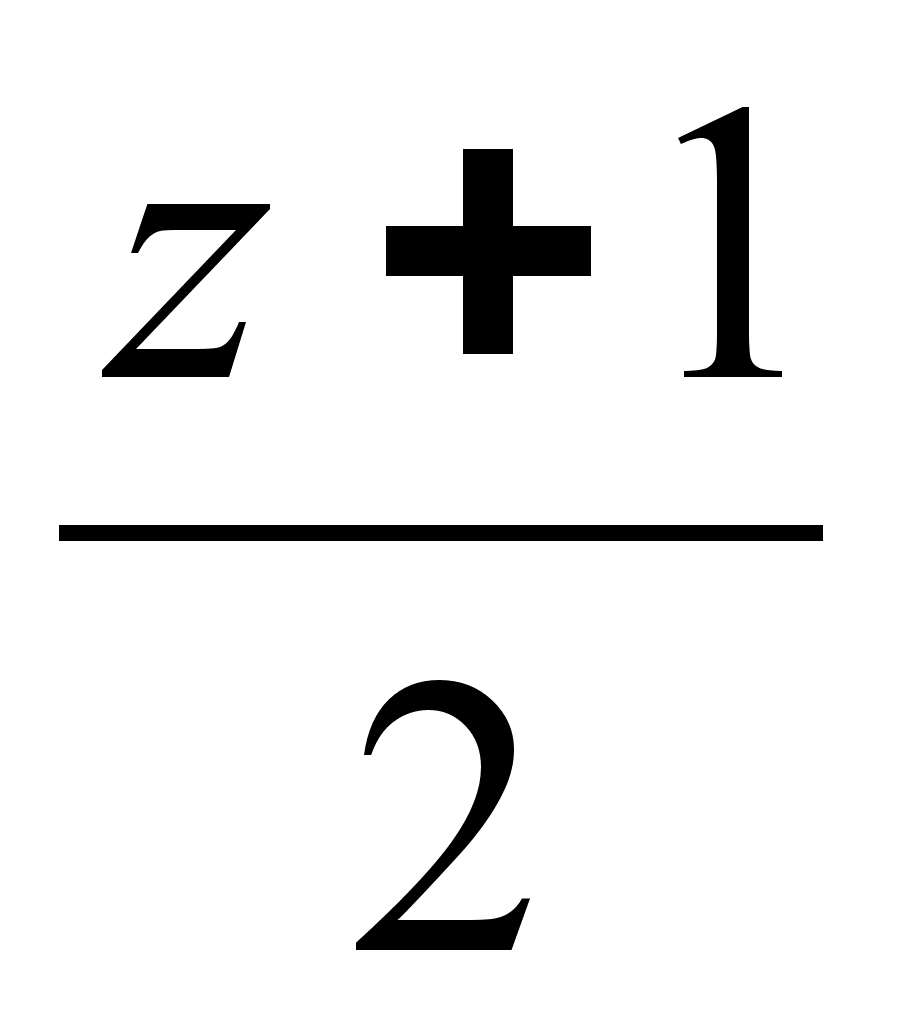 .
.Найти интервалы монотонности функции ƒ(х) = х3 – 9х2 + 15х +1.
На предприятии работает 183 сотрудника. Найти вероятность того, что ровно у двух из них день рождения 31 декабря.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 27
Дать определение дизъюнкции высказываний. Построить дизъюнкцию высказываний «целое число х делится на 6» и «целое число х имеет остаток 3 от деления на 6». Истинна ли дизъюнкция при х = 9?
Как формулируется классическое определение вероятности?
Известно, что высказывания a, – истинны, а с – ложно. Определить истинность высказывания (a

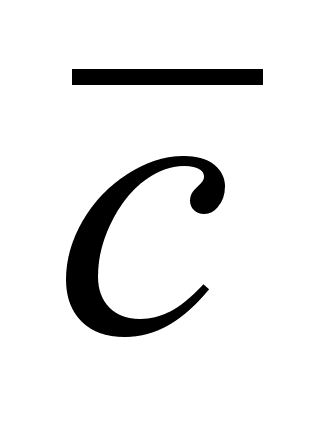 )
) 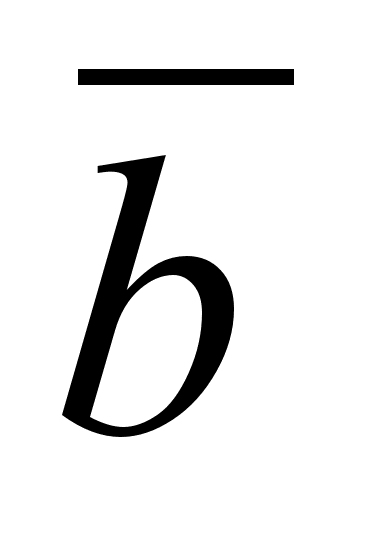 .
.Найти общее уравнение высоты треугольника АВС из точки А, если известно:
А (-3, 0), В (-3, 5), С (5, 3).Найти производную функции f(x) =
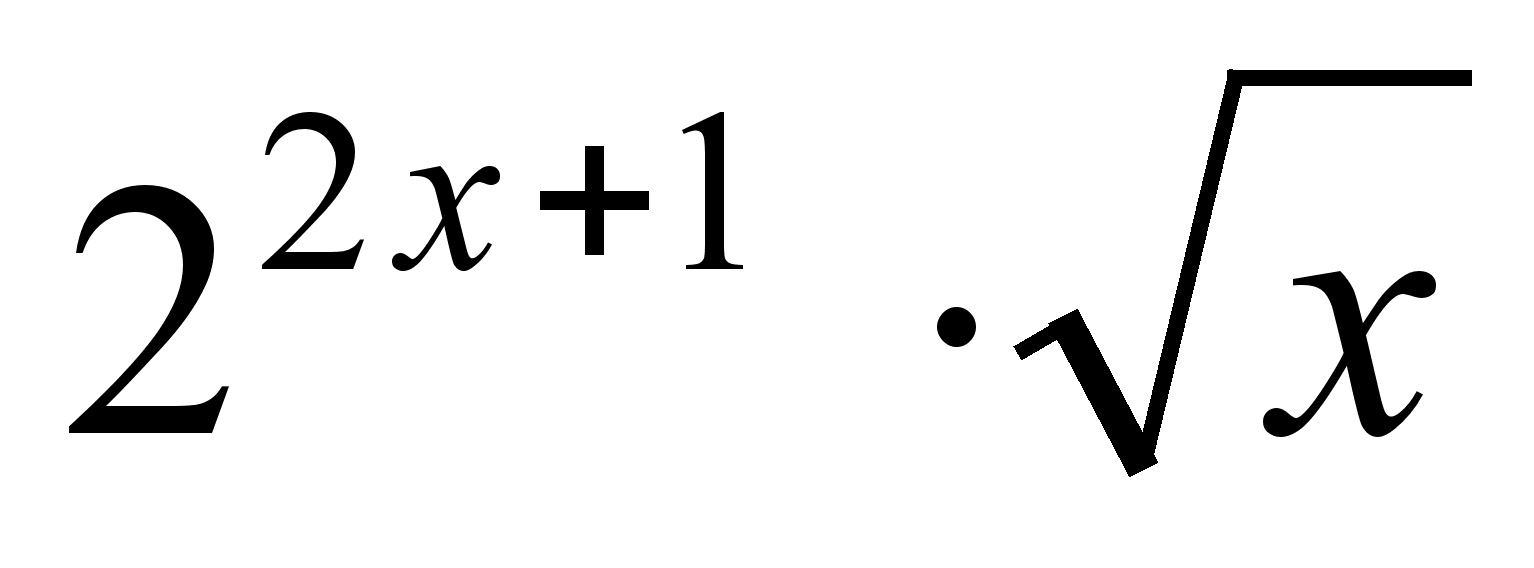 .
.Плотность распределения случайной величины Y такова:
f(x)=0 при х <1 и х > 6, f(x) =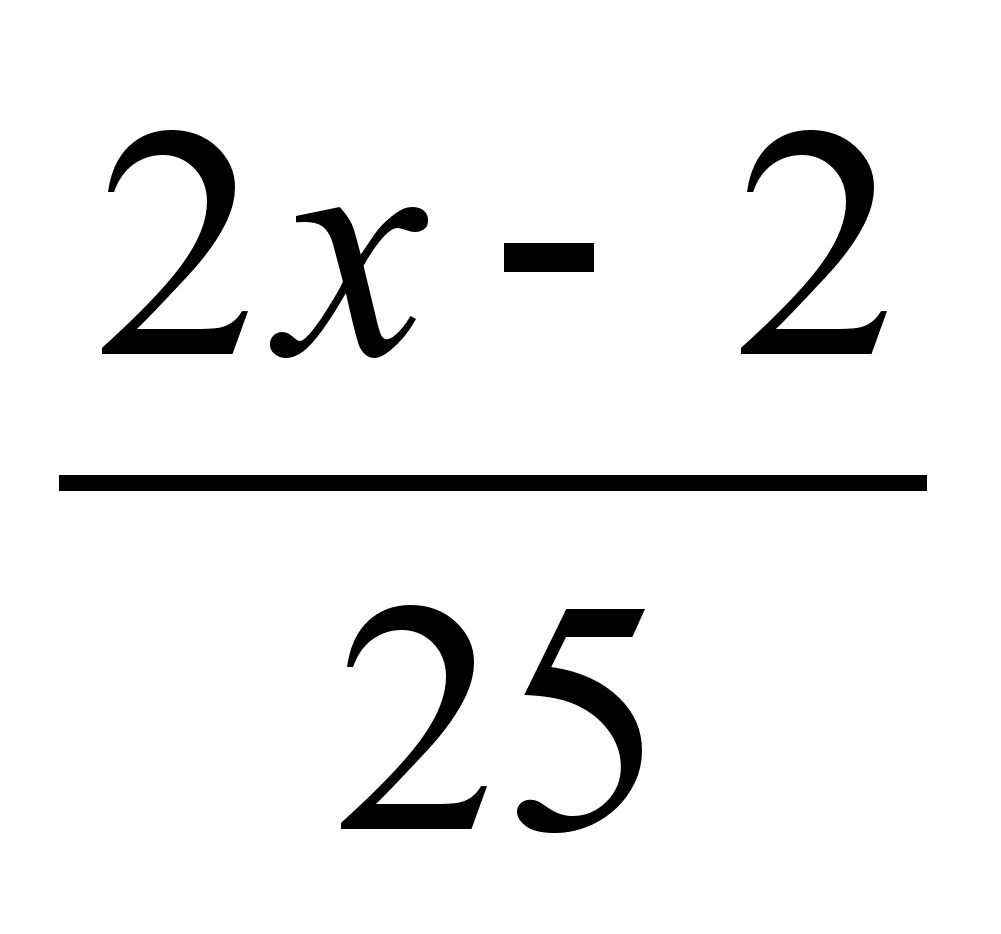 при х∈ (1,6).
при х∈ (1,6).
Найти MY.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 28
Дать определение геометрической прогрессии. Написать формулы для
п-го члена прогрессии и суммы первых п членов. Привести пример применения этих формул.Основные правила вычисления пределов. Что такое неопределенность типа (
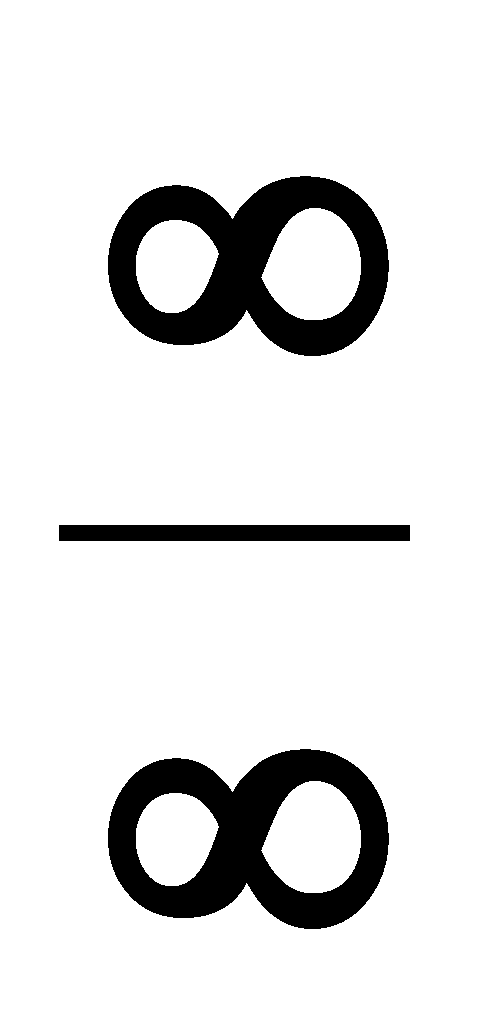 )?
)?Первый член арифметической прогрессии равен 2, а сумма первых 5 равна 0. Найти сумму первых 6 членов.
Найти общее уравнение медианы треугольника АВС из точки А, если известно:
А (2, -5), В (4, 6), С (-2, 0).Вычислить неопределенный интеграл
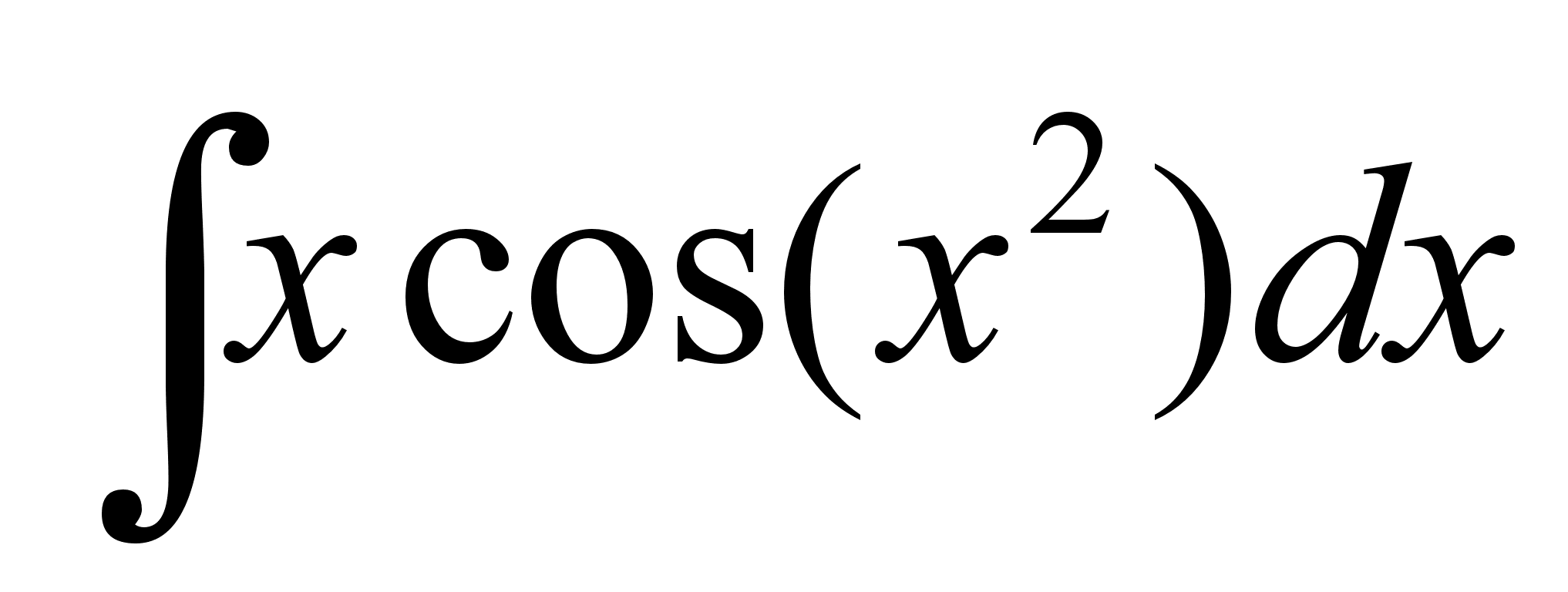 .
.АТС обслуживает 420 звонков в среднем за час. Найти вероятность того, что за данную минуту будет обслужено ровно 5 звонков.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 29
Дать определение графика числовой функции. Начертить графики функций
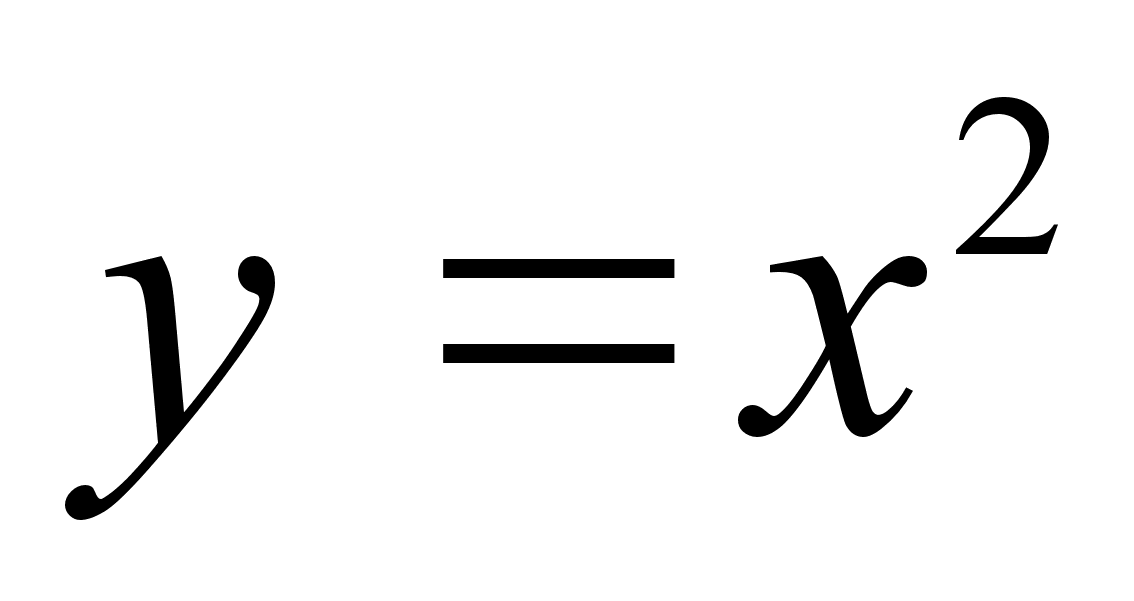 и
и 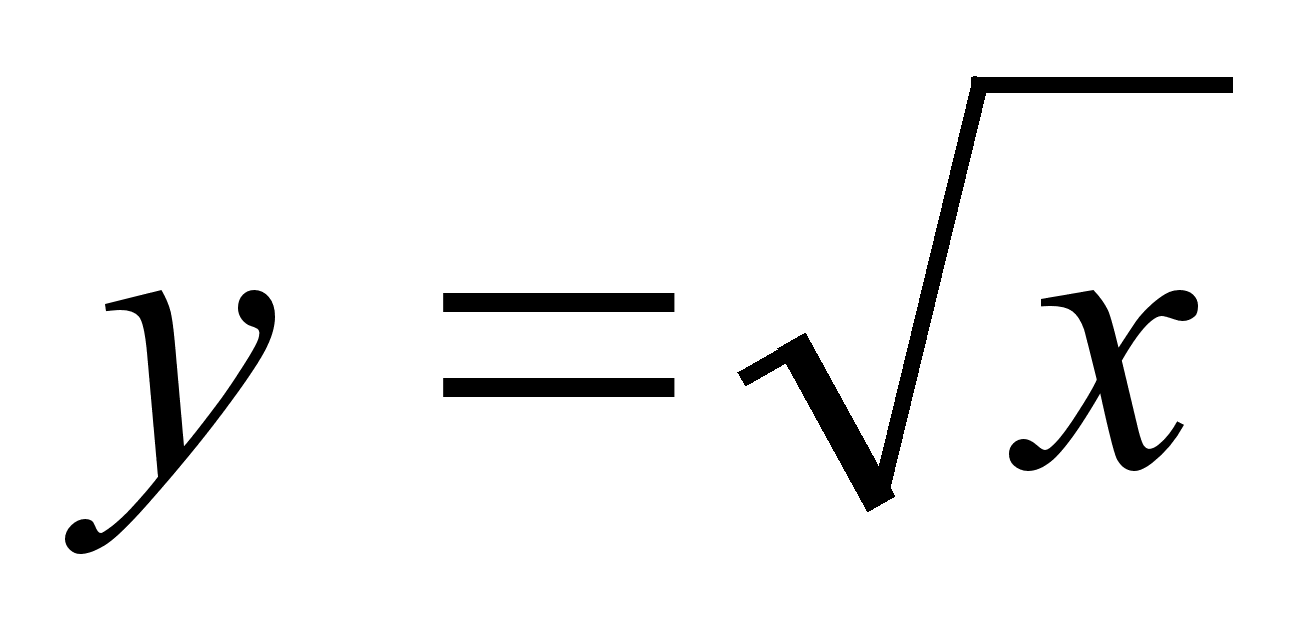 .
.Формула Ньютона – Лейбница. Привести пример применения формулы.
Даны числовые множества: А = {3х | хцелое}, В = {2х | х целое},С=(-9,10). Найти
(А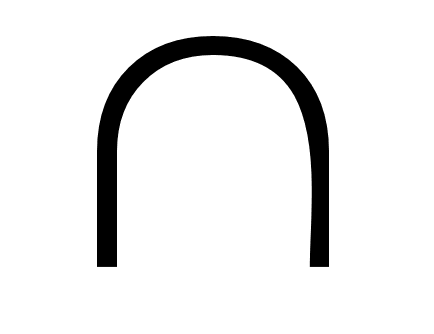 С) \ В.
С) \ В.Найти косинус угла между векторами
 и
и 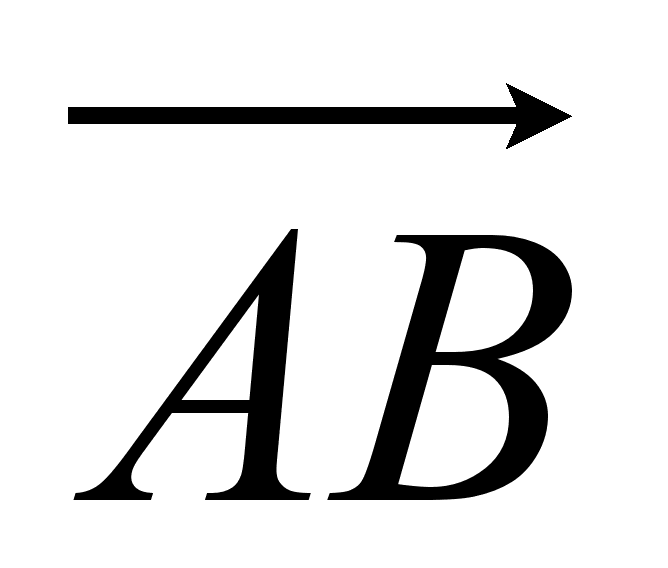 , если известно:
, если известно:  {-2, 3, 1}, А (1, 5, 3), В (-2, 7, 4).
{-2, 3, 1}, А (1, 5, 3), В (-2, 7, 4).Найти производную функции ƒ(х) =
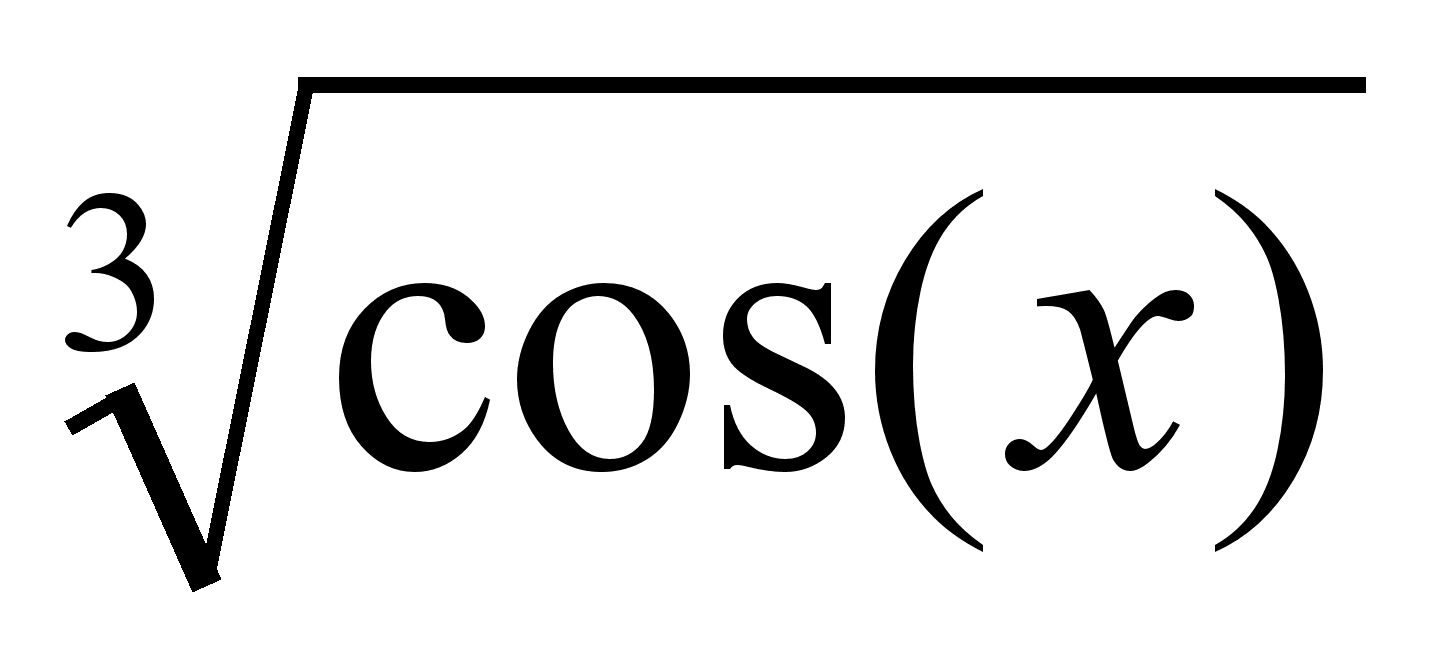 .
.На склад поступает продукция 3-х фабрик, причем продукция первой фабрики составляет 20%, второй - 46%, третьей - 34%. Известно также, что средний процент нестандартных изделий для первой фабрики равен 3%, для второй - 2%, для третьей - 1%. Чему равна вероятность того, что наудачу взятое изделие произведено на третьей фабрике, если оно оказалось нестандартным?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 30
Дать определение графика числовой функции. Начертить графики функций y = ex и
y = ln x.Правило дифференцирования сложной функции. Привести пример.
Найти область определения функции ƒ(х) =
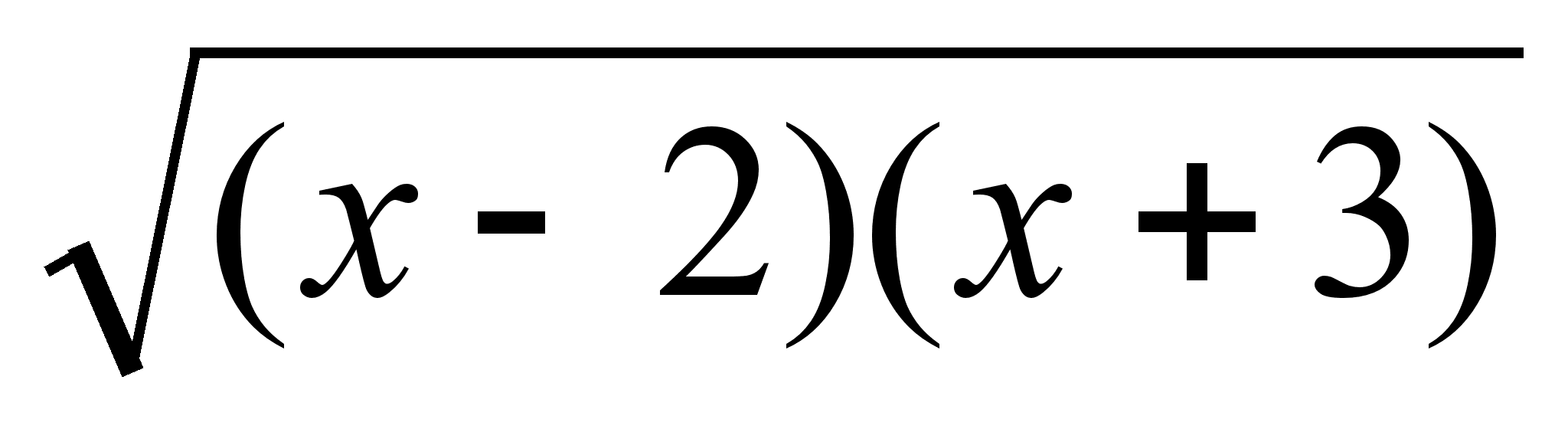 +
+ 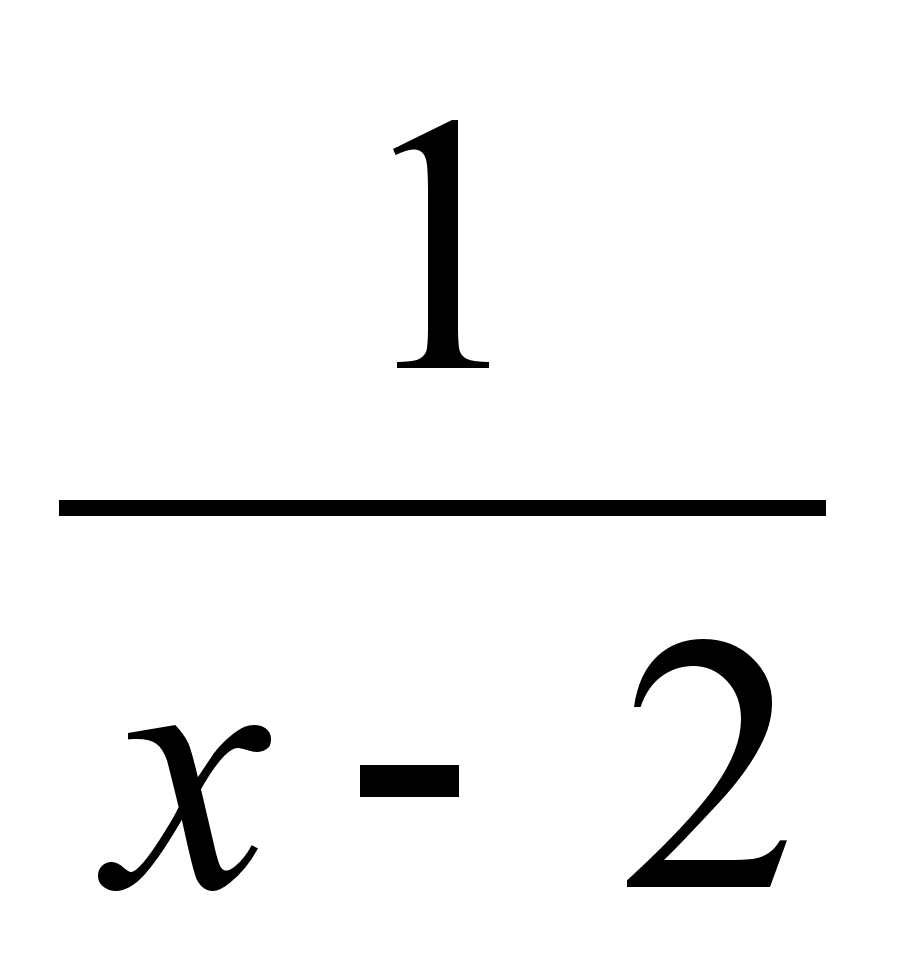 .
.Найти косинус угла между векторами
 и
и 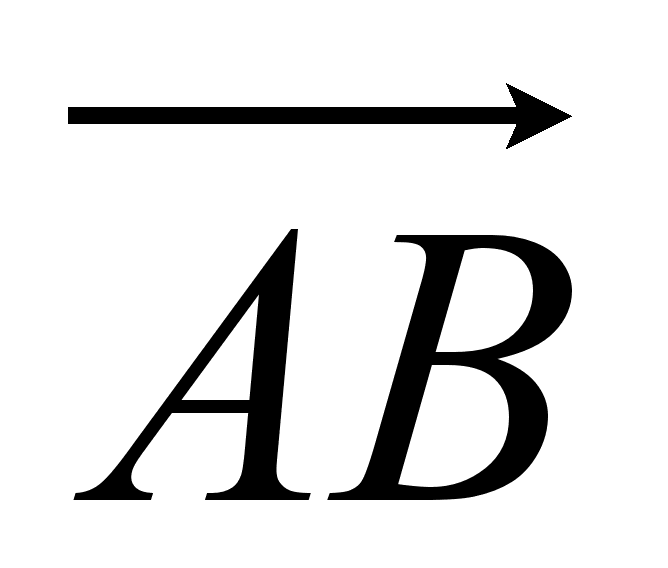 , если известно:
, если известно:  {3, -1, 2}, А (-1, -3, 0), В (2, -2, 2).
{3, -1, 2}, А (-1, -3, 0), В (2, -2, 2).Найти производную функции f(x) =
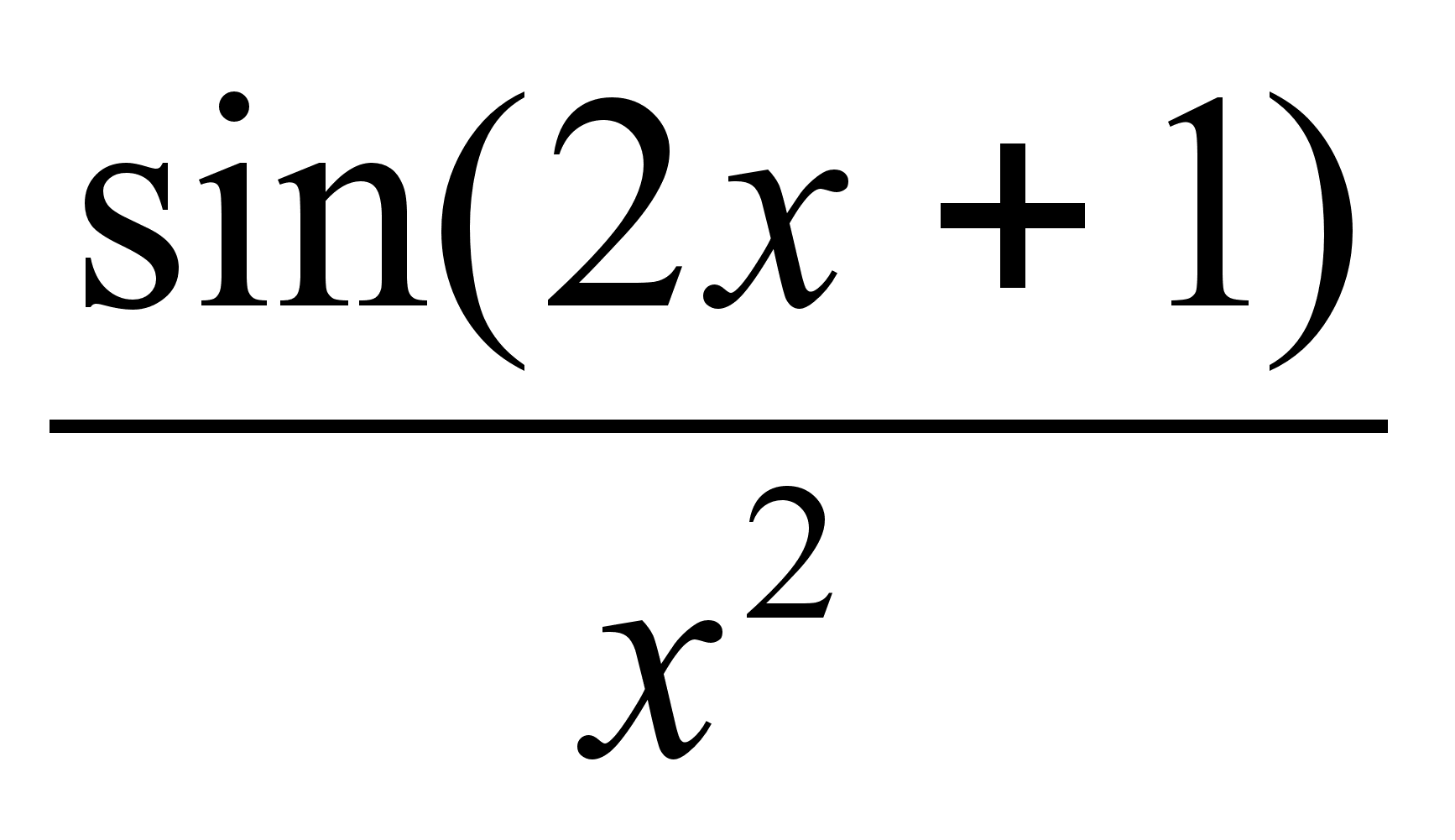 .
.Случайная величина X задана рядом распределения:
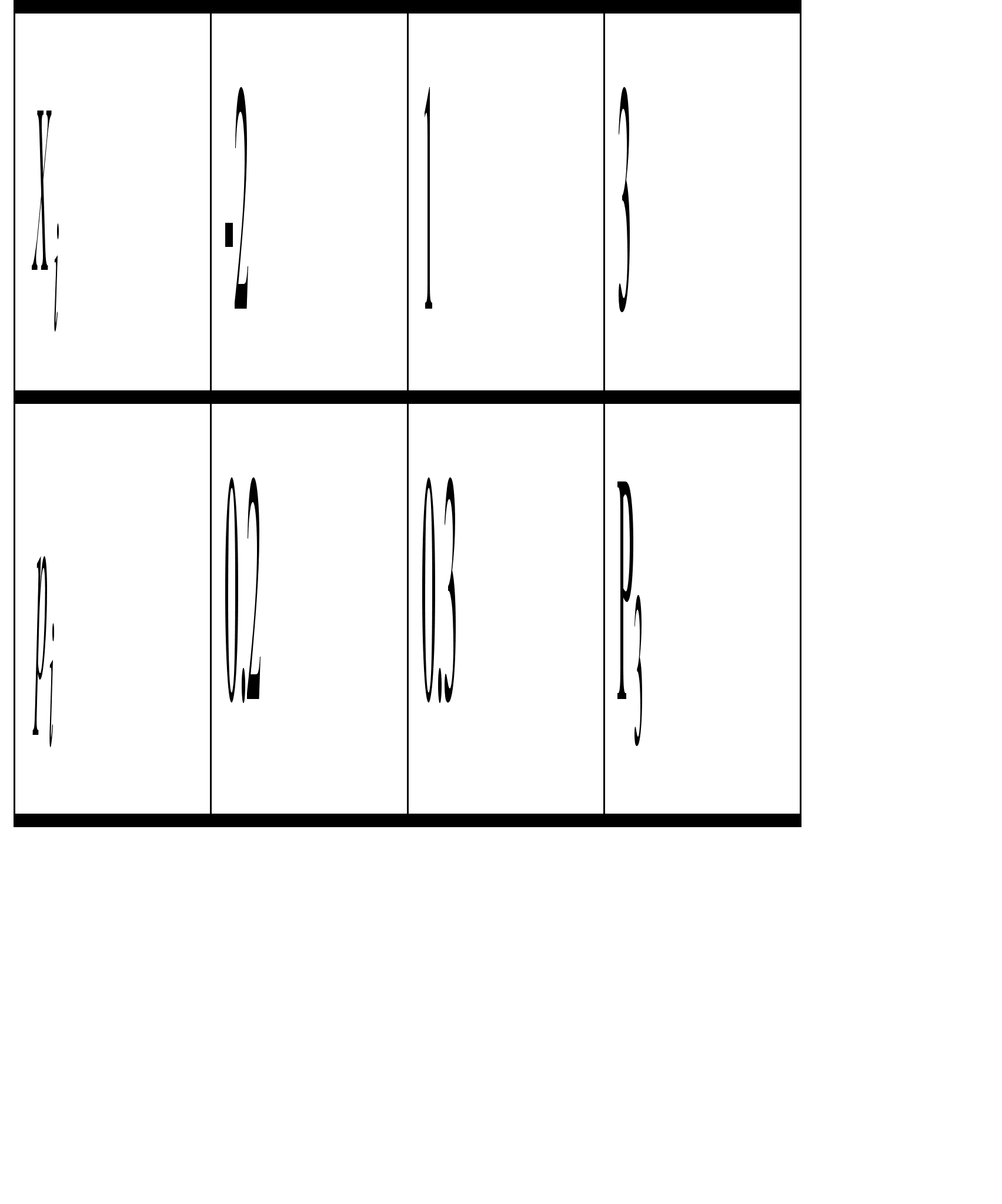
найти Р3 и DX.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 31
Дать определение пересечения множеств, показав его на диаграммах Венна. Привести пример пересечения числовых множеств.
Правило замены переменной под знаком интеграла. Привести пример.
Даны числовые множества: А = {4х | хцелое}, В = {х2 | х целое}, С=(-4,19). Найти
(А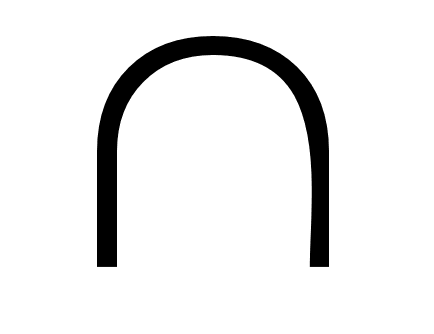 С) \ В.
С) \ В.Найти координаты вершин и фокусов гиперболы 25х2 - 9у2 = 225.
Вычислить площадь фигуры, ограниченной линией
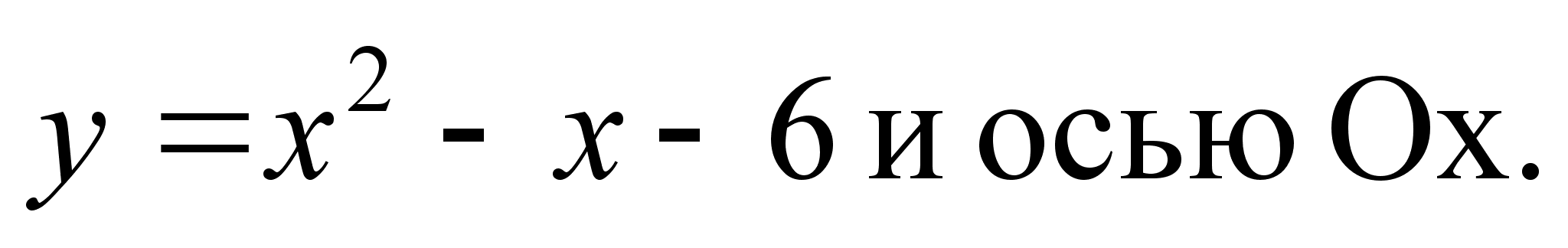 .
.Плотность распределения случайной величины Y такова:
f(x)=0 при х < -1 и х > 3, f(x) =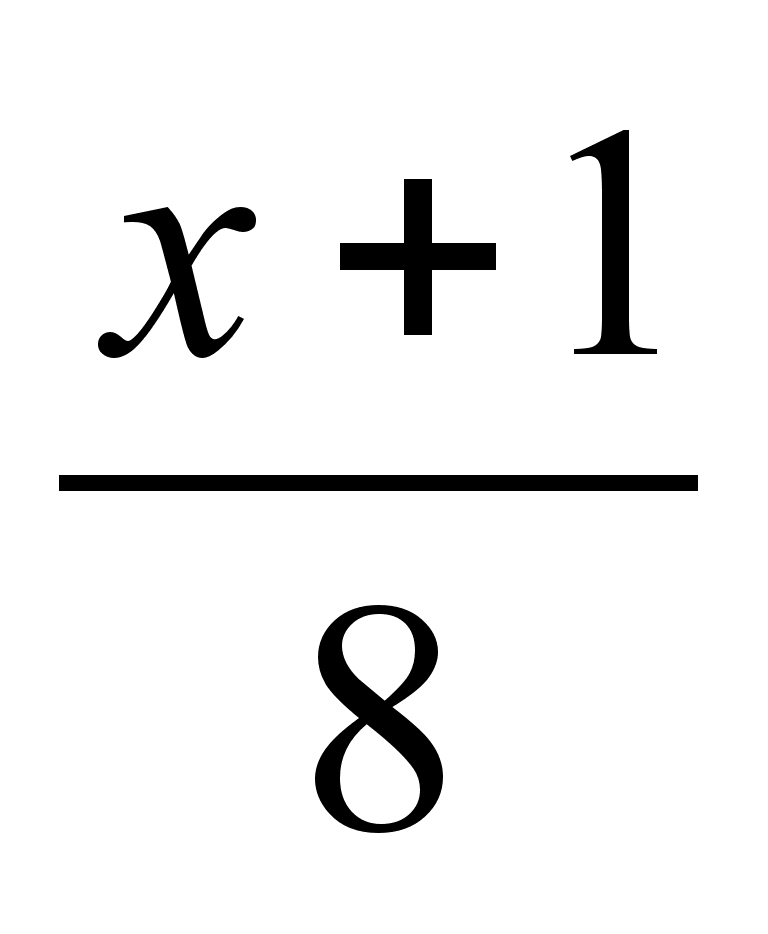 при х∈ (-1,3).
при х∈ (-1,3).
Найти вероятность того, что случайная величина Y больше 2.
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 32
Дать определение области определения и области значений числовой функции. Описать области определения и значений функции y =
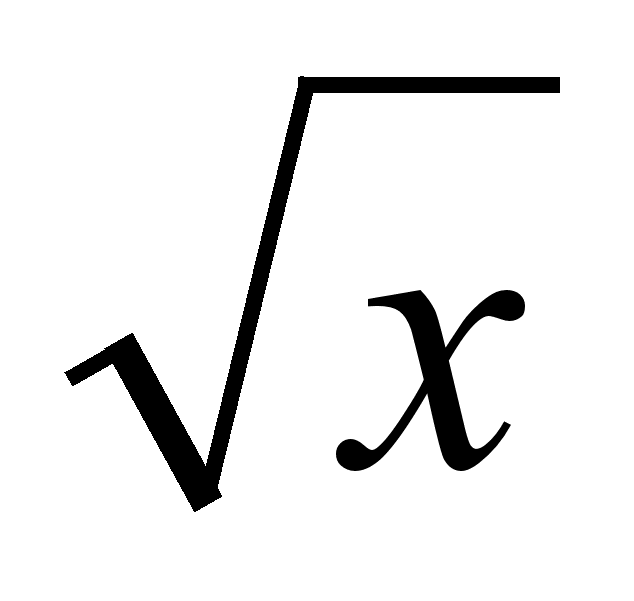 .
.Как определяется нормальное распределение? В чем смысл центральной предельной теоремы?
В группе, состоящей из 42 человек, 23 студентов интересуются юриспруденцией, 15 – экономикой, 5 – и тем и другим. Сколько студентов не интересуются этими дисциплинами?
Написать уравнение плоскости, проходящей через точку (-2, 1, -5) перпендикулярно прямой
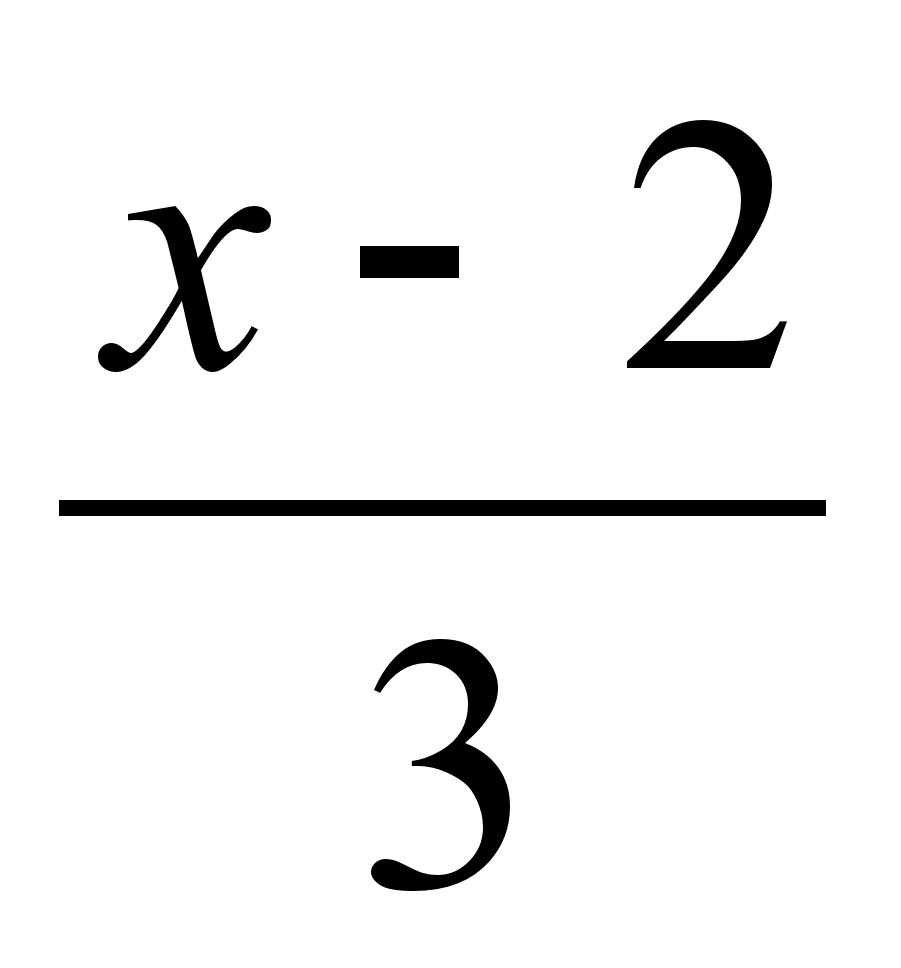 =
= 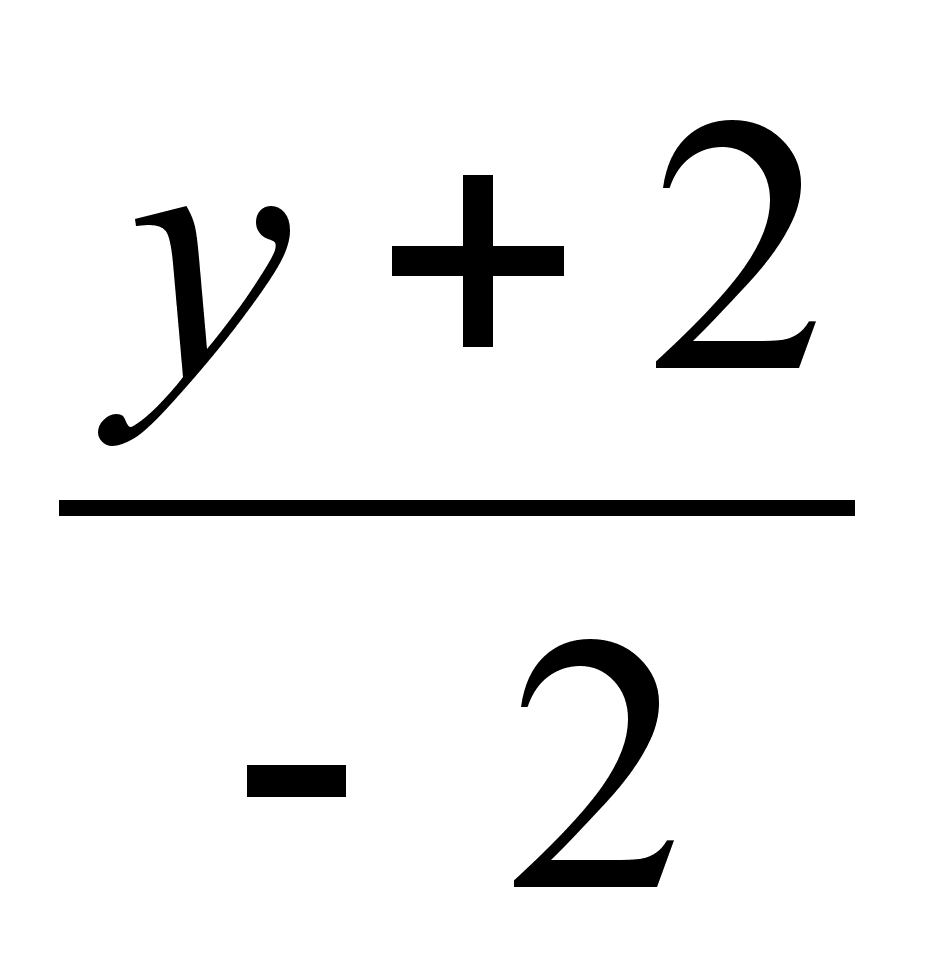 =
= 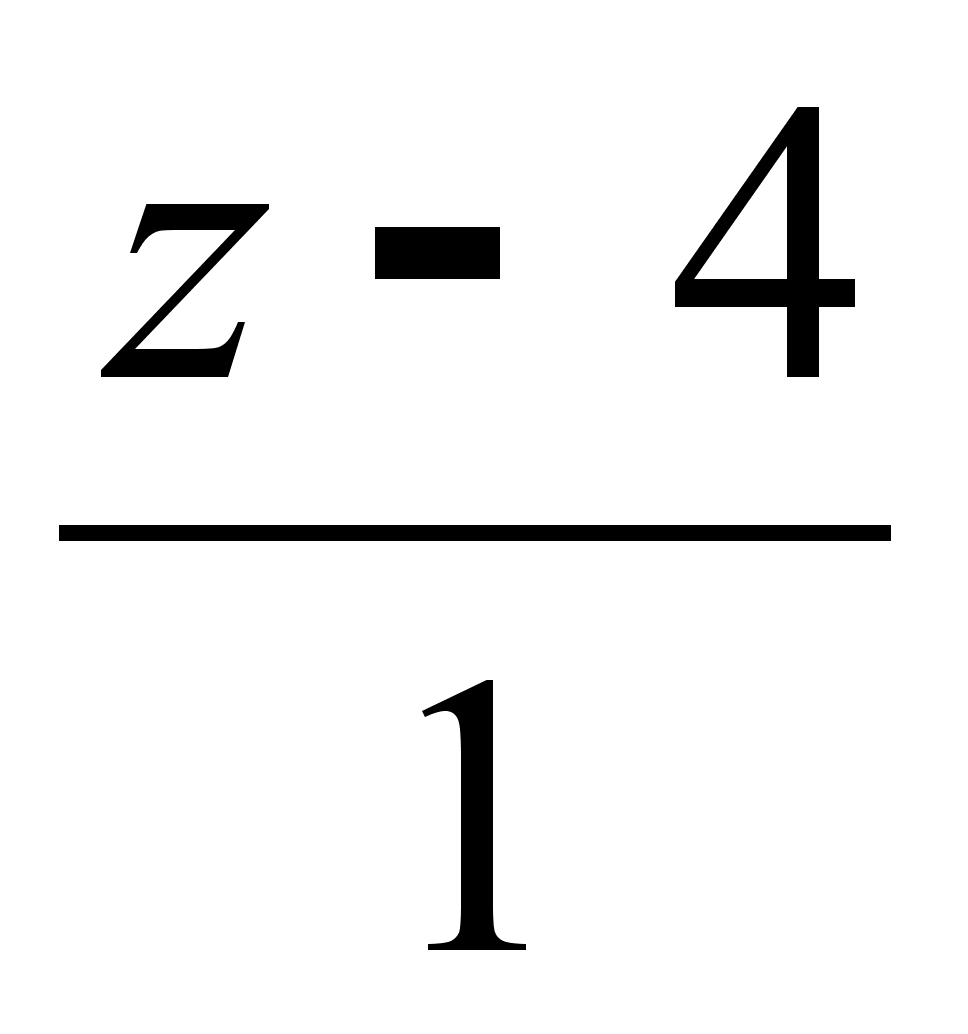 .
.Найти точки экстремума функции ƒ(х) = х3 – 9х2 +15х + 3.
Чему равна вероятность того, что при 4-х подбрасываниях игральной кости выпадет 3? Выпадет 3 ровно 1 раз?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 33
Дать определение суммы векторов. Свойства операции сложения. Сумма векторов, заданных своими координатами. Привести пример.
Определение вертикальной и наклонной асимптот графика функции. Алгоритм нахождения наклонной асимптоты.
Даны числовые множества: А = {х3 | хцелое}, В = {2х | х целое},С=(-27, 9). Найти
(А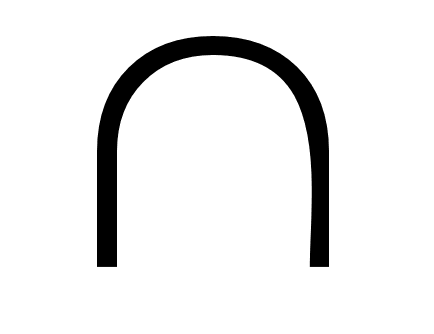 С) \ В.
С) \ В.Написать уравнение параболы с вершиной в начале координат и горизонтальной директрисой, причем парабола проходит через точку (-3, -27).
Вычислить неопределенный интеграл
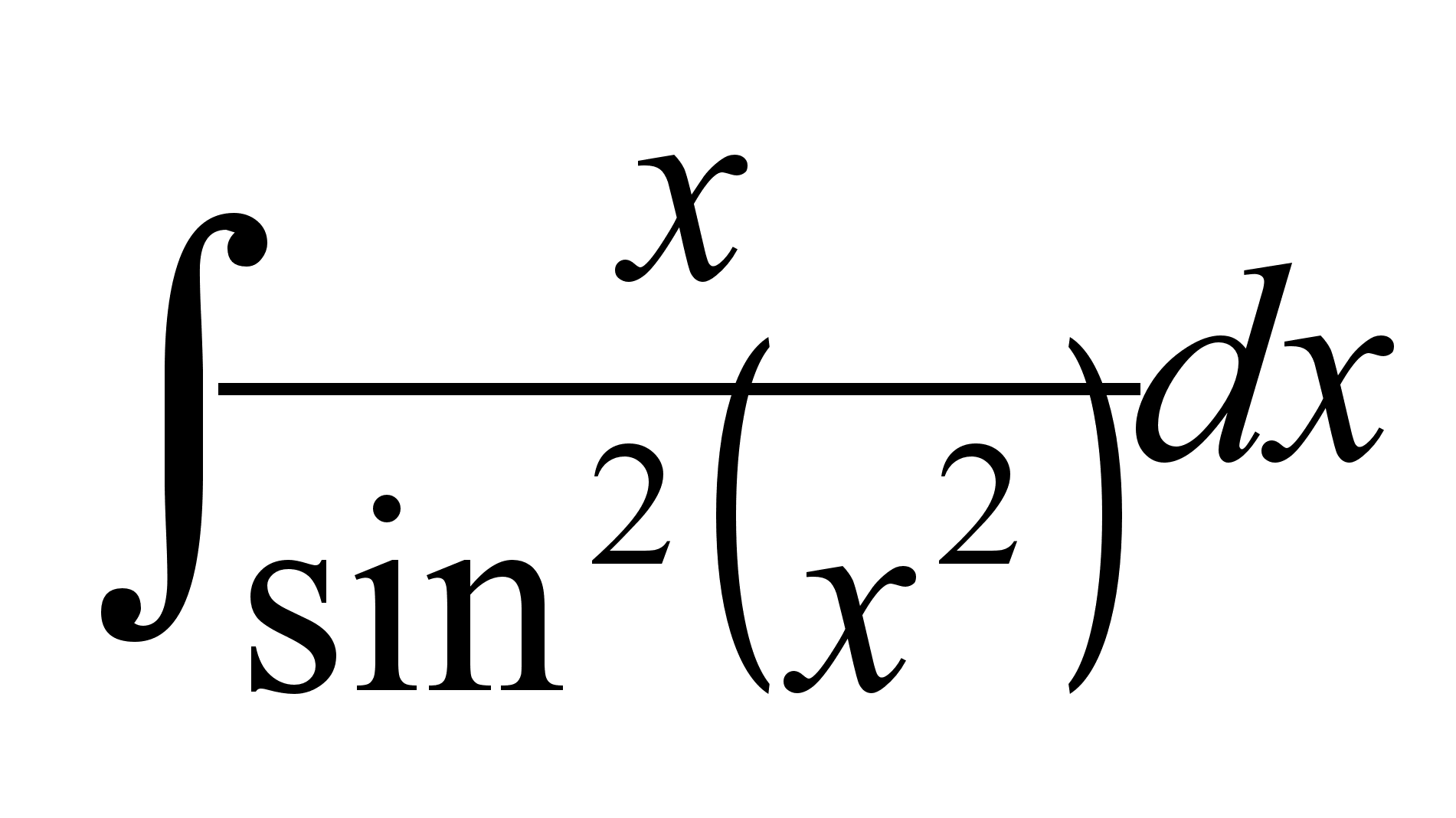 .
.Для разрушения моста достаточно одного попадания. На мост сбросили 4 бомбы, вероятность попадания которых равна 0.3, 0.4, 0.6 и 0.7 соответственно. Какова вероятность того, что мост будет разрушен?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 34
Объясните понятия: необходимое, достаточное, необходимое и достаточное условие. Привести примеры для каждого из них.
Определение точки локального максимума функции. Необходимое условие максимума. Достаточное условие максимума. Привести пример применения достаточного условия.
В трудовом коллективе из 35 человек каждый является или начальником или подчиненным. Начальников 13, а подчиненных 34. Сколько сотрудников являются и начальниками, и подчиненными?
Найти длину вектора 2
 – 3
– 3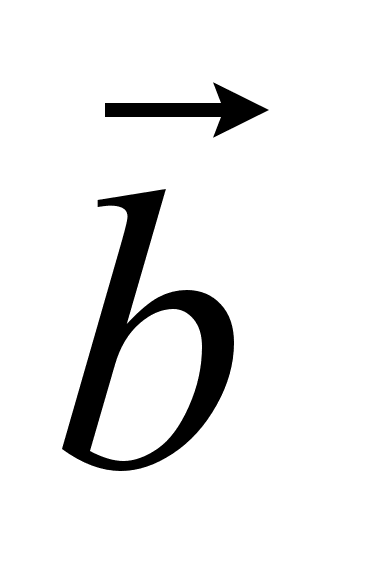 , если дано:
, если дано:  {3, 1, -2},
{3, 1, -2}, 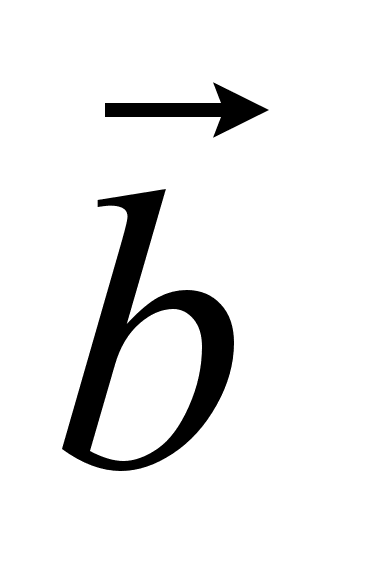 {1, -1, -3}.
{1, -1, -3}.Найти производную функции ƒ(х) = sin (
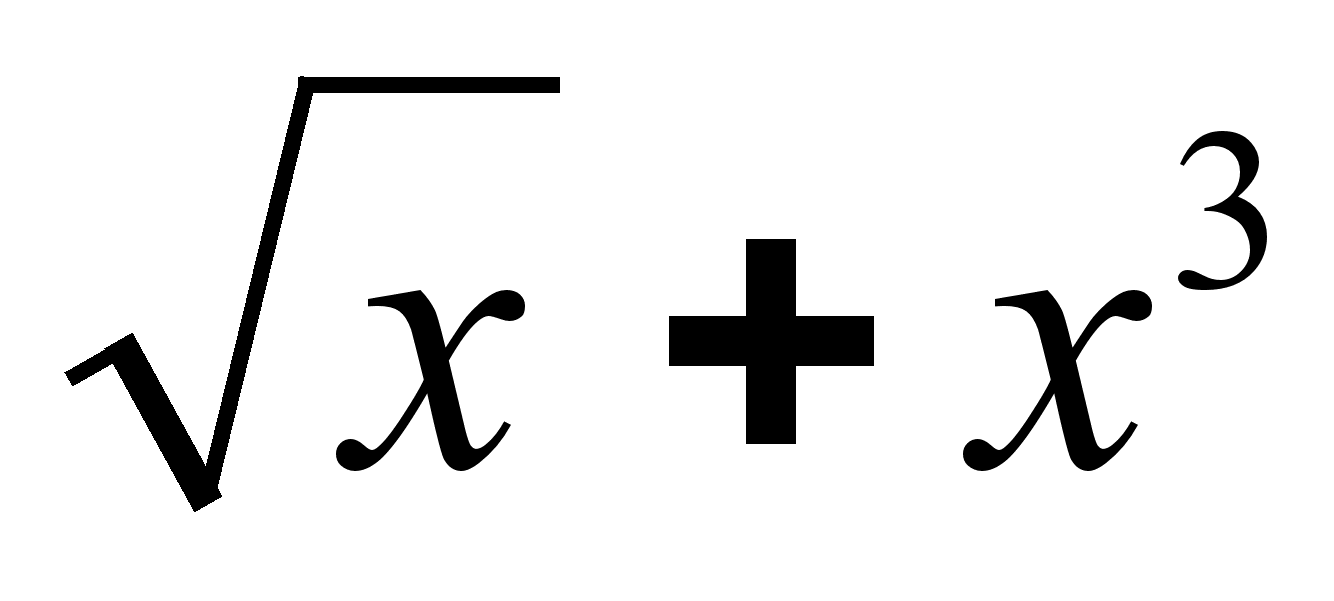 ).
).Шифр замка состоит из 4 цифр. Какова вероятность открыть замок с первого раза, набрав правильную комбинацию? Какова вероятность открыть замок с первого раза, набрав правильную комбинацию цифр, если последняя цифра нечетная?
Зав. кафедрой
--------------------------------------------------
Экзаменационный билет по предмету
МАТЕМАТИКА. БАЗОВЫЙ КУРС (ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ)
Билет № 35
Дать геометрическое определение гиперболы. Что такое фокусы, вершины, центр? Нарисовать чертеж гиперболы и показать на нем вышеупомянутые точки.
Как вводятся числовые характеристики дискретной случайной величины - математическое ожидание, дисперсия, среднеквадратическое отклонение? Какой смысл имеют эти характеристики?
Определить, какие из точек К (0, -4), L(-2, -1), M (-4, 1) принадлежат множеству
А = {(x,y) :1 - х ≥ y ≥ x2 -4}.Найти координаты вершин и фокусов гиперболы -4х2 + 25у2 = 100.
Найти точки перегиба функции ƒ(х) = х4 - 2х3 +х - 2.
На диспетчерский пункт аварийной службы поступает в среднем 5 заявок в минуту. Найти верояность того, что в данную минуту поступит не больше трех заявок.
Зав. кафедрой
--------------------------------------------------
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Экстремумы функций
Содержание.1. Введение………………………………………………32. Историческая справка………………………………..43. Экстремумы функций одной переменной. 3.
- Элементы теории устойчивости
- Серьёзные лекции по высшей экономической математике
- Cпособы преобразования комплексного чертежа, применение при изображении предметов
План. 1. Введение2. Основная частьа) понятие «комплексный чертеж»б) комплексные проекциив) двухпроекционный комплексный чертежг) оси
- Кривые линии и поверхности
Министерство образования Российской ФедерацииРязанская Государственная Радиотехническая АкадемияКафедра НГЧРефератпо инженерной и
- Начертательная геометрия и инженерная графика
- Основные концепции физики ХХ века
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

