Шпаргалка по математике
Формулы сокр. умножения и разложения на множители :
(a±b)²=a²±2ab+b²
(a±b)³=a³±3a²b+3ab²±b³
a²-b²=(a+b)(a-b)
a³±b³=(a±b)(a²∓ab+b²),
(a+b)³=a³+b³+3ab(a+b)
(a-b)³=a³-b³-3ab(a-b)
xn-an=(x-a)(xn-1+axn-2+a²xn-3+...+an-1)
ax²+bx+c=a(x-x1)(x-x2)
где x1 и x2 — корни уравнения
ax²+bx+c=0
Степени и корни :
ap·ag = ap+g
ap:ag=a p-g
(ap)g=a pg
ap /bp = (a/b)p
ap×bp = abp
a0=1; a1=a
a-p = 1/a
pÖa =b => bp=a
pÖapÖb = pÖab
Öa ; a = 0
____
/ __ _
pÖ gÖa = pgÖa
___ __
pkÖagk = pÖag
p ____
/ a pÖa
/ ¾¾ = ¾¾¾¾
Ö b pÖb
a 1/p = pÖa
pÖag = ag/p
Квадратное уравнение
ax²+bx+c=0; (a¹0)
x1,2= (-b±ÖD)/2a; D=b² -4ac
D>0® x1¹x2 ;D=0® x1=x2
D<0, корней нет.
Теорема Виета:
x1+x2 = -b/a
x1× x2 = c/a
Приведенное кв. Уравнение:
x² + px+q =0
x1+x2 = -p
x1×x2 = q
Если p=2k (p-четн.)
и x²+2kx+q=0, то x1,2 = -k±Ö(k²-q)
Нахождение длинны отр-ка
по его координатам
Ö((x2-x1)²-(y2-y1)²)
Логарифмы:
loga x = b => ab = x; a>0,a¹0
a loga x = x, logaa =1; loga 1 = 0
loga x = b; x = ab
loga b = 1/(log b a)
logaxy = logax + loga y
loga x/y = loga x - loga y
loga xk =k loga x (x >0)
logak x =1/k loga x
loga x = (logc x)/( logca); c>0,c¹1
logbx = (logax)/(logab)
Прогрессии
Арифметическая
an = a1 +d(n-1)
Sn = ((2a1+d(n-1))/2)n
Геометрическая
bn = bn-1 × q
b2n = bn-1× bn+1
bn = b1×qn-1
Sn = b1 (1- qn)/(1-q)
S= b1/(1-q)
Тригонометрия.
sin x = a/c
cos x = b/c
tg x = a/b=sinx/cos x
ctg x = b/a = cos x/sin x
sin (p-a) = sin a
sin (p/2 -a) = cos a
cos (p/2 -a) = sin a
cos (a + 2pk) = cos a
sin (a + 2pk) = sin a
tg (a + pk) = tg a
ctg (a + pk) = ctg a
sin² a + cos² a =1
ctg a = cosa / sina , a ¹ pn, nÎZ
tga × ctga = 1, a ¹ (pn)/2, nÎZ
1+tg²a = 1/cos²a , a¹p(2n+1)/2
1+ ctg²a =1/sin²a , a¹ pn
Формулы сложения:
sin(x+y) = sin x cos y + cos x sin y
sin (x-y) = sin x cos y - cos x sin y
cos (x+y) = cos x cos y - sin x sin y
cos (x-y) = cos x cos y + sin x sin y
tg(x+y) = (tg x + tg y)/ (1-tg x tg y )
x, y, x + y ¹ p/2 + pn
tg(x-y) = (tg x - tg y)/ (1+tg x tg y)
x, y, x - y ¹ p/2 + pn
Формулы двойного аргумента.
sin 2a = 2sin a cos a
cos 2a = cos² a - sin² a = 2 cos² a - 1 =
= 1-2 sin²a
tg 2a = (2 tga)/ (1-tg²a)
1+ cos a = 2 cos² a/2
1-cosa = 2 sin² a/2
tga = (2 tg (a/2))/(1-tg²(a/2))
Ф-лы половинного аргумента.
sin² a/2 = (1 - cos a)/2
cos²a/2 = (1 + cosa)/2
tg a/2 = sina/(1 + cosa ) = (1-cos a)/sin a
a¹ p + 2pn, n ÎZ
Ф-лы преобразования суммы в произв.
sin x + sin y = 2 sin ((x+y)/2) cos ((x-y)/2)
sin x - sin y = 2 cos ((x+y)/2) sin ((x-y)/2)
cos x + cos y = 2cos (x+y)/2 cos (x-y)/2
cos x - cos y = -2sin (x+y)/2 sin (x-y)/2
sin (x+y)
tg x + tg y = —————
cos x cos y
sin (x - y)
tg x - tgy = —————
cos x cos y
Формулы преобр. произв. в сумму
sin x sin y = Ѕ(cos (x-y) - cos (x+y))
cos x cos y = Ѕ(cos (x-y)+ cos (x+y))
sin x cos y = Ѕ(sin (x-y)+ sin (x+y))
Соотнош. между ф-ями
sin x = (2 tg x/2)/(1+tg2x/2)
cos x = (1-tg2 2/x)/ (1+ tg² x/2)
sin2x = (2tgx)/(1+tg2x)
sin²a = 1/(1+ctg²a) = tg²a/(1+tg²a)
cos²a = 1/(1+tg²a) = ctg²a / (1+ctg²a)
ctg2a = (ctg²a-1)/ 2ctga
sin3a = 3sina -4sin³a = 3cos²asina-sin³a
cos3a = 4cos³a-3 cosa=
= cos³a-3cosasin²a
tg3a = (3tga-tg³a)/(1-3tg²a)
ctg3a = (ctg³a-3ctga)/(3ctg²a-1)
sin a/2 = ±Ö((1-cosa)/2)
cos a/2 = ±Ö((1+cosa)/2)
tga/2 = ±Ö((1-cosa)/(1+cosa))=
sina/(1+cosa)=(1-cosa)/sina
ctga/2 = ±Ö((1+cosa)/(1-cosa))=
sina/(1-cosa)= (1+cosa)/sina
sin(arcsin a) = a
cos( arccos a) = a
tg ( arctg a) = a
ctg ( arcctg a) = a
arcsin (sina) = a ; aÎ (-p/2 ; p/2)
arccos(cos a) = a ; a Î (0 ; p)
arctg (tg a) = a ; a Î(-p/2 ; p/2)
arcctg (ctg a) = a ; a Î ( 0 ; p)
arcsin(sina)=
1)a - 2pk; aÎ(-p/2 +2pk;p/2+2pk)
2) (2k+1)p - a; aÎ(p/2+2pk;3p/2+2pk)
arccos (cosa) =
1) a-2pk ; aÎ(2pk;(2k+1)p)
2) 2pk-a ; aÎ((2k-1)p; 2pk)
arctg(tga)= a-pk
aÎ(-p/2 +pk;p/2+pk)
arcctg(ctga) = a -pk
aÎ(pk; (k+1)p)
arcsina = -arcsin (-a)= p/2-arccosa =
= arctg a/Ö(1-a²)
arccosa = p-arccos(-a)=p/2-arcsin a=
= arc ctga/Ö(1-a²)
arctga =-arctg(-a) = p/2 -arcctga =
= arcsin a/Ö(1+a²)
arc ctg a = p-arc cctg(-a) =
= arc cos a/Ö(1-a²)
arctg a = arc ctg1/a =
= arcsin a/Ö(1+a²)= arccos1/Ö(1+a²)
arcsin a + arccos = p/2
arcctg a + arctga = p/2
Тригонометрические уравнения
sin x = m ; |m| = 1
x = (-1)narcsin m + pk, kÎ Z
sin x =1 sin x = 0
x = p/2 + 2pk x = pk
sin x = -1
x = -p/2 + 2 pk
cos x = m; |m| = 1
x = ± arccos m + 2pk
cos x = 1 cos x = 0
x = 2pk x = p/2+pk
cos x = -1
x = p+ 2pk
tg x = m
x = arctg m + pk
ctg x = m
x = arcctg m +pk
sin x/2 = 2t/(1+t2); t - tg
cos x/2 = (1-t²)/(1+t²)
Показательные уравнения.
Неравенства: Если af(x)>(<) aа(ч)
1) a>1, то знак не меняеться.
2) a<1, то знак меняется.
Логарифмы : неравенства:
logaf(x) >(<) log a j(x)
1. a>1, то : f(x) >0
j(x)>0
f(x)>j(x)
2. 0
j(x)>0
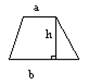
f(x) 3. log f(x) j(x) = a ОДЗ: j(x) > 0 f(x) >0 f(x ) ¹ 1 Тригонометрия: 1. Разложение на множители: sin 2x - Ö3 cos x = 0 2sin x cos x -Ö3 cos x = 0 cos x(2 sin x - Ö3) = 0 .... 2. Решения заменой .... 3. sin² x - sin 2x + 3 cos² x =2 sin² x - 2 sin x cos x + 3 cos ² x = 2 sin² x + cos² x Дальше пишеться если sin x = 0, то и cos x = 0, а такое невозможно, => можно поделить на cos x Тригонометрические нер-ва : sin a ³ m 2pk+a1 = a = a2+ 2pk 2pk+a2 = a= (a1+2p)+ 2pk Пример: I cos (p/8+x) < Ö3/2 pk+ 5p/6< p/8 +x< 7p/6 + 2pk 2pk+ 17p/24 < x< p/24+2pk;;;; II sin a = 1/2 2pk +5p/6 =a= 13p/6 + 2pk cos a ³(=) m 2pk + a1 < a< a2+2 pk 2pk+a2< a< (a1+2p) + 2pk cos a ³ - Ö2/2 2pk+5p/4 =a= 11p/4 +2pk tg a³(=) m pk+ arctg m =a= arctg m + pk ctg ³(=) m pk+arcctg m < a< p+pk Производная: (xn)’ = n× xn-1 (ax)’ = ax× ln a (lg ax )’= 1/(x×ln a) (sin x)’ = cos x (cos x)’ = -sin x (tg x)’ = 1/cos² x (ctg x)’ = - 1/sin²x (arcsin x)’ = 1/ Ö(1-x²) (arccos x)’ = - 1/ Ö(1-x²) (arctg x)’ = 1/ Ö(1+x²) (arcctg x)’ = - 1/ Ö(1+x²) Св-ва: (u × v)’ = u’×v + u×v’ (u/v)’ = (u’v - uv’)/ v² Уравнение касательной к граф. y = f(x0)+ f ’(x0)(x-x0) уравнение к касательной к графику в точке x 1. Найти производную 2. Угловой коофициент k = = производная в данной точке x 3. Подставим X0, f(x0), f ‘ (x0), выразим х Интегралы : ò xn dx = xn+1/(n+1) + c ò ax dx = ax/ln a + c ò ex dx = ex + c ò cos x dx = sin x + cos ò sin x dx = - cos x + c ò 1/x dx = ln|x| + c ò 1/cos² x = tg x + c ò 1/sin² x = - ctg x + c ò 1/Ö(1-x²) dx = arcsin x +c ò 1/Ö(1-x²) dx = - arccos x +c ò 1/1+ x² dx = arctg x + c ò 1/1+ x² dx = - arcctg x + c Площадь криволенейной трапеции. Геометрия Треугольники a + b + g =180 Теорема синусов a² = b²+c² - 2bc cos a b² = a²+c² - 2ac cos b c² = a² + b² - 2ab cos g Медиана дели треуг. на два равновеликих. Медиана делит противопол. сторону напополам. Биссектриса - угол. Высота падает на пр. сторону под прямым углом. Формула Герона : p=Ѕ(a+b+c) _____________ S = Öp(p-a)(p-b)(p-c) S = Ѕab sin a Sравн.=(a²Ö3)/4 S = bh/2 S=abc/4R S=pr Трапеция. S = (a+b)/2× h Круг S= pR² Sсектора=(pR²a)/360 Стереометрия Параллепипед V=Sосн×Р Прямоугольный V=abc Пирамида V =1/3Sосн.×H Sполн.= Sбок.+ Sосн. Усеченная : H . _____ V = 3 (S1+S2+ÖS1S2) S1 и S2 — площади осн. Sполн.=Sбок.+S1+S2 Конус V=1/3 pR²H Sбок. =pRl Sбок.= pR(R+1) Усеченный Sбок.= pl(R1+R2) V=1/3pH(R12+R1R2+R22) Призма V=Sосн.×H прямая: Sбок.=Pосн.×H Sполн.=Sбок+2Sосн. наклонная : Sбок.=Pпс×a V = Sпс×a, а -бок. ребро. Pпс — периметр Sпс — пл. перпенд. сечения Цилиндр. V=pR²H ; Sбок.= 2pRH Sполн.=2pR(H+R) Sбок.= 2pRH Сфера и шар . V = 4/3 pR³ - шар S = 4pR³ - сфера Шаровой сектор V = 2/3 pR³H H - высота сегм. Шаровой сегмент V=pH²(R-H/3) S=2pRH 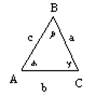
град 0° 30° 45° 60° 90° 120° 135° 180° a -p/2 -p/3 -p/4 -p/6 0 p/6 p/4 p/3 p/2 2p/3 3p/4 3p/6 p sina -1 -Ö3/2 -Ö2/2 - Ѕ 0 Ѕ Ö2/2 Ö3/2 1 - Ѕ 0 cosa 1 Ö3/2 Ö2/2 Ѕ 0 - Ѕ -Ö2/2 - Ö3/2 -1 tga Ï -Ö3 -1 -1/Ö3 0 1/Ö3 1 Ö3 Î -Ö3 -1 0 ctga --- Ö3 1 1/Ö3 0 -1/Ö3 -1 -- n 2 3 4 5 6 7 8 9 2 4 9 16 25 36 49 64 81 3 8 27 64 125 216 343 512 729 4 16 81 256 625 1296 2401 4096 6561 5 32 243 1024 3125 7776 16807 32768 59049 6 64 729 4096 15625 46656 7 128 2181 8 256 6561 -a p-a p+a p/2-a p/2+a 3p/2 - a 3p/2+a sin -sina sina -sina cosa cosa -cosa -cosa cos cosa -cosa -cosa sina -sina -sina sina tg -tga -tga tga ctga -ctga ctga -ctga ctg -ctga -ctga ctga tga -tga tga -tga
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Ориентация спина фотона
Ориентация спина дискретной поперечной волныТеоретически считается, что спин фотона имеет только продольную ориентацию, но такая точк
- Гравитационное взаимодействие
Энергия вакуумных флуктуаций«В этой теории гравитационное взаимодействие - не фундаментальное взаимодействие, а результат квантовых
- Новые физические законы
Аруцев Александр Артемьевич, Ермолаев Борис Валерьевич, Кутателадзе Ираклий Отарович, Слуцкий Михаил Семенович"Если нам действительн
- Физический вакуум
- Нормальные Алгоритмы Маркова. Построение алгоритмов из алгоритмов.
Нормальные Алгоритмы Маркова.Построение алгоритмов из алгоритмов.В 1956 году отечественным математиком А.А. Марковым было предложено но
- Космическая программа Китая
Идея превращения Китая в мощную мировую державу ныне связывается с реализацией концепции совокупной национальной мощи, в которой особ
- Ссылочный тип данных. Динамические объекты.
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

