Скачать

Чёрные дыры и пространственно-временные парадоксы

“Из всех измышлений человеческого ума, от единорогов и химер до водородной бомбы, наверное, самое фантастическое — это образ черный дыры, отделенной от остального пространства определенной границей, которую ничто не может пересечь; дыры, обладающей настолько сильным гравитационным полем, что даже свет задерживается его мертвой хваткой; дыры, искривляющей пространство и тормозящей время. Подобно единорогам и химерам, черная дыра кажется более уместной в фантастических романах или в мифах древности, чем в реальной Вселенной. И тем не менее законы современной физики фактически требуют, чтобы черные дыры существовали. Возможно, только наша Галактика содержит миллионы их” — так сказал о черных дырах американский физик К. Торн.

1. Черные дыры

Черные дыры — один из самых необыкновенных объектов, предсказываемых общей теорией относительности Эйнштейна. У черных дыр интересная история, поскольку они преподнесли теоретикам немало сюрпризов, приведших к лучшему пониманию природы пространства-времени.

Давайте начнем с теории всемирного тяготения Ньютона. Силу гравитационного притяжения мы испытываем прямо здесь, на поверхности земли. Если подбросить камень, он упадет под действием земного притяжения. А можно ли подбросить камень с такой скоростью, чтобы он на Землю не вернулся? Можно. Если запустить камень со скоростью выше второй космической скорости (около 11 км/с), он покинет гравитационное поле Земли. Эта «скорость выхода» зависит от массы и радиуса земного шара. Если бы Земля при ее нынешнем радиусе была массивнее или имела бы меньший радиус при ее нынешней массе, скорость выхода была бы выше. Возникает вопрос: что будет, если плотность и масса космического тела настолько велики, что скорость выхода из его гравитационного поля выше скорости света? Ответ: такое тело будет представляться внешнему наблюдателю абсолютно черным, поскольку свет его покинуть не может. Например, звезда с радиусом меньше, чем

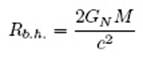
где GN — постоянная Ньютона, а с — скорость света в вакууме, будет выглядеть абсолютно черной.

Для тех, кто не разбирается в формулах, приведу несколько примеров. Чтобы тело, масса которого равна массе Земли, превратилось в черную дыру, оно должно иметь радиус меньше сантиметра. Тело с массой Солнца должно сжаться до диаметра меньше километра. На это еще в конце XVIII века указал Пьер-Симон Лаплас, но тогда никто не придал этому особого значения.

С появлением в 1905 году специальной теории относительности у нас появилось понимание того факта, что скорость света в вакууме — не рядовая скорость. Это космический предел: ничто не может двигаться быстрее света. Теория относительности Эйнштейна также учит нас, что пространство и время тесно взаимосвязаны. Для наблюдателей, движущихся друг относительно друга, время течет с разной скоростью. Предположим, вы стоите на улице и смотрите на проезжающие машины. Для водителей машин время течет чуть медленнее, чем для вас, и несколько иначе. Предположим, вы видите, как два светофора в разных концах улицы одновременно переключаются на красный. Для водителей же они переключатся не одновременно. Это получается после того, как мы учтем время, которое требуется свету, чтобы пройти расстояние от светофора до наблюдателей. И для вас, и для водителей свет движется с одинаковой скоростью, но время для них течет медленнее. То есть, время относительно, а скорость света абсолютна. Это противоречит нашим интуитивным представлениям о мире, так как эффект этот на нас практически не сказывается, поскольку мы обычно путешествуем на скоростях, которые очень далеки от скорости света, а время измеряем не с абсолютной точностью. Однако в ускорителях элементарных частиц этот эффект наблюдается постоянно. При скоростях, близких к скорости света, частицы живут значительно дольше.

Пространство и время объединяются в единую концепцию пространства-времени. Время воспринимается по-разному двумя наблюдателями, движущимися друг относительно друга. Однако оба наблюдателя воспринимают одно и то же пространство-время. Имеются точные формулы, позволяющие нам связать наблюдения этих двух наблюдателей.

Теперь вернемся к гравитации. Она обладает очень важным свойством, которое открыл еще Галилей: все тела падают одинаково, если не учитывать сопротивление воздуха. В безвоздушном пространстве пушинка и камень упадут на землю одновременно. В случае действия других сил это не так. В электрическом поле заряженная частица будет двигаться иначе в случае изменения ее массы или заряда. В теории всемирного тяготения Ньютона причина, по которой все тела движутся под воздействием гравитационных сил одинаково, сводится к тому, что сила гравитационного притяжения пропорциональна массе тела. Иногда это называют «принципом эквивалентности».

Эйнштейн осознал, что теория Ньютона противоречит теории относительности, поскольку согласно ньютоновской теории гравитационное взаимодействие между телами передается мгновенно. В 1915 году Эйнштейн решил эту проблему таким образом, что из этого решения естественным путем вытекает и принцип эквивалентности. Свою новую концепцию Эйнштейн назвал общей теорией относительности. Он предположил, что гравитация возникает вследствие искривления пространства-времени. В искривленном пространстве-времени частицы движутся по кратчайшим траекториям. Изначально параллельные линии таких траекторий в искривленном пространстве-времени могут сближаться. Например, два земных меридиана на пересечении с экватором параллельны, однако по мере удаления от него они сближаются и, в конечном итоге, пересекаются в точке Северного полюса. Конфигурация пространства-времени зависит от материи, перемещающейся в нем. Общая теория относительности подразумевает, что темп времени зависит от гравитационного поля. Следовательно, два жильца одного дома, обитающие на первом и последнем этажах, воспринимают ход времени по-разному. Для обитателя первого этажа время течет чуть медленнее, чем для обитателя верхнего этажа. Для земных зданий этот эффект пренебрежимо мал и составляет порядка 10–15 секунды за секунду. Главное, что нам нужно усвоить, это то, что массивные тела стягивают пространство-время на себя. В частности, вблизи массивных объектов время течет медленнее, чем на удалении от них.

Физики всегда стремятся сначала разобрать простейшие ситуации. Поэтому в 1916 году, вскоре после открытия общей теории относительности, молодой немецкий физик Карл Шварцшильд (Karl Schwarzschield) нашел простейшее сферически симметричное решение уравнений Эйнштейна. Это решения описывает частный случай искривления геометрии пространства-времени под воздействием точечной массы. Однако, вместо геометрии, давайте обратим внимание на другой их аспект: темп хода стационарных часов. Часы на поверхности Солнца идут на одну миллионную медленнее, чем удаленные от Солнца часы. Часы на поверхности нейтронной звезды идут со скоростью 70% от скорости часов вдали от нее. Здесь налицо уже весьма значительный эффект расхождения во времени. Так вот, решение Шварцшильда подразумевает, что часы в «центре» точечной массы вообще остановились бы. Поначалу физики сочли это «нефизическим» парадоксом, следствием слишком упрощенного анализа.

Дальнейшие расчеты показали, однако, что речь в решении Шварцшильда идет даже не о некоем условном «центре», а о целой идеальной сфере. Путешественник, пересекающий границы этой сферы и попадающий внутрь нее, не испытывает ничего странного или необычного — для него время течет по-прежнему. А вот для сторонних наблюдателей за пределами этой сферы, принимающих сигналы от падающего внутрь сферы путешественника, любые сигналы от него будут неуклонно замедляться, пока не исчезнут, как таковые, при пересечении им поверхности сферы. Поверхность, на которой стационарные часы замедляются до нуля, принято называть сферой Шварцшильда или «горизонтом». Возврата из-за горизонта нет. Наблюдатель, пересекший его и попавший внутрь сферы, обратно не выберется и будет неизбежно поглощен сингулярностью в ее центре. «Сингулярность» — это область сверхвысокого искривления пространства-времени, и путешественник в ней попросту исчезнет и будет раздавлен огромной гравитационной силой. Выясняется, что размер черной дыры согласно теории Эйнштейна описывается все той же формулой, предложенной еще Лапласом в рамках механики Ньютона, однако ее физическая интерпретация в корне меняется.

Черные дыры могут образовываться в результате астрофизических процессов, когда у звезд с массой, на порядок превышающей массу Солнца, кончается термоядерное топливо, и они обрушиваются внутрь себя под действием гравитационных сил. Имеется достаточно данных наблюдений, свидетельствующих о реальности существования таких черных дыр во Вселенной. С астрофизической точки зрения обнаруженные черные дыры подразделяются на две категории. Первый тип — это черные дыры, образовавшиеся в результате коллапса массивных звезд и обладающие соответствующей массой. Поскольку черные дыры кажутся нам реально черными, наблюдать их крайне сложно. Если посчастливится, мы можем увидеть лишь шлейф газа, затягиваемого в черную дыру. Разгоняясь при падении, газ разогревается и испускает характерное излучение, которое мы только и можем обнаружить. Источником газа при этом является другая звезда, образующая парную систему с черной дырой и обращающаяся вместе с ней вокруг центра масс двойной звездной системы. Иными словами, сначала мы имели обычную двойную звезду, затем одна из звезд в результате гравитационного коллапса превратилась в черную дыру. После этого черная дыра начинает засасывать газ с поверхности горячей звезды. Второй тип — это гораздо более массивные черные дыры в центрах галактик. Их масса превышает массу Солнца в миллиарды раз. Опять же, падая на такие черные дыры, вещество разогревается и испускает характерное излучение, которое со временем доходит до Земли, его-то мы и можем обнаружить. Предполагается, что все крупные галактики, включая нашу, имеют в центре свою черную дыру.

Однако основным предметом нашего разговора является не астрофизика черных дыр, а исследование их влияния на структуру пространства-времени.

Согласно теории Эйнштейна черная дыра представляет собой бездонный провал в пространстве-времени, падение в который необратимо. Что упало, то пропало в черной дыре навеки.

У черных дыр очень интересные свойства. После коллапса звезды в черную дыру ее свойства будут зависеть только от двух параметров: массы и углового момента вращения. То есть, черные дыры представляют собой универсальные объекты, то есть, их свойства не зависят от свойств вещества, из которого они образованы. При любом химическом составе вещества исходной звезды свойства черной дыры будут одними и теми же. То есть, черные дыры подчиняются только законам теории гравитации — и никаким иным.

Другое любопытное свойство черных дыр заключается в следующем: предположим, вы наблюдаете процесс, в котором участвует черная дыра. Например, можно рассмотреть процесс столкновения двух черных дыр. В результате из двух черных дыр образуется одна более массивная. Этот процесс может сопровождаться излучением гравитационных волн, и уже построены детекторы с целью их обнаружения и измерения. Процесс этот теоретически просчитать весьма непросто, для этого нужно решить сложную систему дифференциальных уравнений. Однако имеются и простые теоретические результаты. Площадь сферы Шварцшильда получившейся черной дыры всегда больше суммы площадей поверхностей двух исходных черных дыр. То есть, при слиянии черных дыр площадь их поверхности растет быстрее массы. Это так называемая «теорема площадей», она была доказана Стивеном Хокингом (Steven Hawking) в 1970 году.

2.Образование черных дыр.

Процессы образования первичных черных дыр с массой, меньшей солнечной, могли происходить лишь в адронную эру, когда средняя плотность вещества была достаточно высока. Первичных черных дыр образуется тем больше, тем больше была амплитуда начальных неоднородностей и чем “мягче” уравнения состояния вещества в момент их образования. Дальнейшая судьба первичных черных дыр зависит от их массы. Черные дыры с массой от 1015 до 1033 г могли бы доживать до настоящего времени и оказаться “живыми свидетелями” процессов, происходивших во времени 10-23—10-5 с после “большого взрыва”.

Пока в недрах звезды происходят термоядерные реакции, они поддерживают высокую температуру и давление, препятствуя сжатию звезды под действием собственной гравитации. Однако со временем ядерное топливо истощается, и звезда начинает сжиматься. Расчеты показывают, что если масса звезды не превосходит трех масс Солнца, то она выиграет «битву с гравитацией»: ее гравитационный коллапс будет остановлен давлением «вырожденного» вещества, и звезда навсегда превратится в белый карлик или нейтронную звезду. Но если масса звезды более трех солнечных, то уже ничто не сможет остановить ее катастрофического коллапса и она быстро уйдет под горизонт событий, став черной дырой. У сферической черной дыры массы M горизонт событий образует сферу с окружностью по экватору в 2p раз большей «гравитационного радиуса» черной дыры RG = 2GM/c2, где c – скорость света, а G – постоянная тяготения. Черная дыра с массой 3 солнечных имеет гравитационный радиус 8, 8 км.

Момент превращения звезды в чёрную дыру

Если астроном будет наблюдать звезду в момент ее превращения в черную дыру, то сначала он увидит, как звезда все быстрее и быстрее сжимается, но по мере приближения ее поверхности к гравитационному радиусу сжатие начнет замедляться, пока не остановится совсем. При этом приходящий от звезды свет будет слабеть и краснеть, пока не потухнет совсем. Это происходит потому, что в борьбе с гигантской силой тяжести свет теряет энергию и ему требуется все больше времени, чтобы достичь наблюдателя. Когда поверхность звезды достигнет гравитационного радиуса, покинувшему ее свету потребуется бесконечное время, чтобы достичь наблюдателя (и при этом фотоны полностью потеряют свою энергию). Следовательно, астроном никогда не дождется этого момента и тем более не увидит того, что происходит со звездой под горизонтом событий. Но теоретически этот процесс исследовать можно.

Расчет идеализированного сферического коллапса показывает, что за короткое время звезда сжимается в точку, где достигаются бесконечно большие значения плотности и тяготения. Такую точку называют «сингулярностью». Более того, общий математический анализ показывает, что если возник горизонт событий, то даже несферический коллапс приводит к сингулярности. Однако все это верно лишь в том случае, если общая теория относительности применима вплоть до очень маленьких пространственных масштабов, в чем мы пока не уверены. В микромире действуют квантовые законы, а квантовая теория гравитации пока не создана. Ясно, что квантовые эффекты не могут остановить сжатие звезды в черную дыру, а вот предотвратить появление сингулярности они могли бы.

Современная теория звездной эволюции и наши знания о звездном населении Галактики указывают, что среди 100 млрд. ее звезд должно быть порядка 100 млн. черных дыр, образовавшихся при коллапсе самых массивных звезд. К тому же черные дыры очень большой массы могут находиться в ядрах крупных галактик, в том числе и нашей.

Как уже отмечалось, в нашу эпоху черной дырой может стать лишь масса, более чем втрое превышающая солнечную. Однако сразу после Большого взрыва, с которого ок. 15 млрд. лет назад началось расширение Вселенной, могли рождаться черные дыры любой массы. Самые маленькие из них в силу квантовых эффектов должны были испариться, потеряв свою массу в виде излучения и потоков частиц. Но «первичные черные дыры» с массой более 1015 г могли сохраниться до наших дней.

Эта трёхмерная иллюстрация показывает, как вблизи вращающейся чёрной дыры перекручиваются силовые линии магнитного поля в падающей на чёрную дыру плазме. Чёрная сфера в центре рисунка - это сама чёрная дыра, а жёлтая область вокруг неё представляет область закрученного пространства. Красные линии показывают силовые линии магнитного поля, проходящие через область закрученного пространства, а зелёные - силовые линии, ещё не входящие в эту область.

Современные суперкомпьютеры имитируют мощные энергетические джеты (струи), выходящие из чёрных дыр - самых экзотических и мощных объектов во Вселенной.

"Эти исследования помогут нам открыть загадку чёрных дыр и подтвердить, что вследствие их вращения действительно происходит выход энергии, " - говорит астрофизик Дэвид Мейер (David Meier), один из соавторов статьи, которая скоро выйдет в международном научном журнале Science.

Чёрные дыры - это сверхплотные объекты с такой сильной гравитацией, что даже свет не может из них выйти. Чёрные дыры захватывают в себя звёзды и любое другое, приблизившееся к ним, вещество, включая другие чёрные дыры. Эти необычные объекты образуются одним из двух способов - при коллапсе звезды или когда много звёзд и чёрных дыр коллапсируют вместе в ядре галактики.

Оба типа чёрных дыр могут вращаться очень быстро, увлекая за собой пространство вокруг них. Когда много вещества падает на чёрную дыру, оно закручивается как в водовороте. С помощью рентгеновских и радио-наблюдений астрономы могут быть свидетелями таких событий, в том числе и струй из чёрных дыр, но они не могут увидеть саму чёрную дыру.

"Мы не можем совершить путешествие к чёрной дыре, и мы не можем сделать её в лаборатории - поэтому мы используем суперкомпьютеры, " - продолжает Мейер. С помощью компьютеров учёные объединяют данные о плазме, падающей на чёрную дыру, и свои познания того, как гравитация и магнитные поля могут воздействовать на плазму. Учёные также исследуют способы того, как магнитное поле может использовать энергию вращения чёрной дыры и образовывать мощные струи.

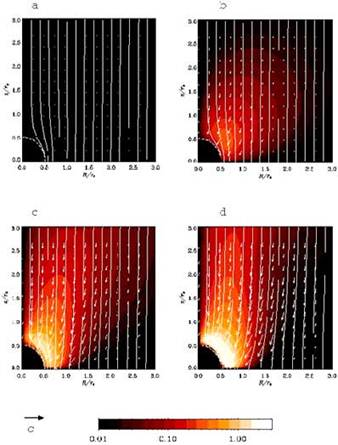
На этих картинках представлена компьютерная эволюция чёрной дыры. Слева вверху - плазма пока медленно падает по направлению к чёрной дыре, силовые линии магнитного поля в плазме показаны белыми линиями. На следующих картинках движение плазмы сильно ускоряется.Однако, вращающаяся чёрная дыра закручивает само пространство (и силовые линии магнитного поля) и испускает мощное электромагнитное излучение вдоль северного и южного полюсов (показано красным и белым цветом), которое захватывает с собой частицы плазмы и образует струи.

Феномен струй был предсказан Роджером Блэндфордом и Романом Знажеком в 1970-х годах. Новые компьютерные исследования подтверждают это предсказание. Последние работы были проведены в конце 2001-го года с помощью суперкомпьютера японского института National Institute for Fusion Science.

Объекты со струями в ядрах галатик были идентифицированы в начале 1900-х годов. В 1960-х годах учёные исследовали возможность того, что этими объекты со струями могут быть сверхмассивные чёрные дыры с массами от одного миллиона до нескольких миллиардов масс Солнца.

В 1990-х годах было установлено, что такие струи могут испукаться менее массивными чёрными дырами в двойных звёздных системах. Чёрная дыра с массой в десять масс Солнца может образоваться при коллапсе звезды массой от 20 до 30 масс Солнца. При этом образуется крошечный невидимый объект размером всего лишь в несколько километров, но с очень мощным гравитационным полем. Сверхмассивные чёрные дыры образуются при коллапсе большого количества звёзд и чёрных дыр в ядрах галактик.

3.Свойства чёрных дыр

Черные дыры имеют много весьма экстравагантных свойств, которыми не обладают другие звезды, даже очень экзотические, вроде нейтронных. Прежде всего, они являются звездами-невидимками. Для того чтобы можно было увидеть предмет, надо, чтобы от него к нам поступил видимый свет. Если предмет невидим в видимом свете, то надо иметь возможность зарегистрировать другое излучение, которое исходит от него: инфракрасное, рентгеновское, радио и т.д. Так вот, очень плотные звезды, которые были названы черными дырами, не посылают в окружающее их пространство абсолютно никакого излучения, поэтому они невидимы ни в каких лучах. Для наблюдателя их просто нет. Само по себе это уже очень странно, поскольку объект, имеющий определенную массу и температуру, что-то должен излучать. Тем более что температура черных дыр может достигать миллиардов градусов. В чем дело?

Такую ситуацию предвидел еще знаменитый французский математик и астроном П. Лаплас. Он описал ее в своей книге "Изложение систем мира", которая вышла в свет в 1795 году. Он рассуждал так. Если для того, чтобы оторваться от данного космического объекта, тело должно иметь скорость (первую космическую скорость) не меньше строго определенной величины, которая определяется массой этого объекта, то при слишком большой его массе скорость тела должна превысить скорость света для того, чтобы оторваться от объекта. Цифры говорят о следующем. Первая космическая скорость на Земле равна 7, 2 км/с, на Луне — 2, 4, на поверхности Юпитера — 61 и на Солнце — 620 км/с. На нейтронной звезде она должна достигать половины скорости света (150 тысяч километров в секунду). Таким образом, если масса звезды еще больше, то первая космическая скорость может превысить скорость света. Эти рассуждения применимы одинаковым образом и к телам, и к фотонам, то есть свету. Если масса звезды такова, что первая космическая скорость для нее должна быть больше скорости света, то свет от этой звезды исходить не может, он не может оторваться от нее, поскольку его скорость меньше первой космической скорости и не может быть ей равна (скорость света не может быть больше скорости света). Лаплас рассчитал, какая это должна быть масса небесного объекта (звезды или планеты). Он писал в указанной книге: "Светящаяся звезда с плотностью, равной плотности Земли, и диаметром в 250 раз больше диаметра Солнца, не дает ни одному световому лучу достичь нас из-за своего тяготения: поэтому возможно, что самые яркие небесные тела во Вселенной оказываются по этой причине невидимыми". Так что, казалось бы, объяснение первого и самого экзотического свойства черной дыры было найдено еще за полтора столетия до ее открытия. Но это и так, и не так. Если говорить строго, то ситуацию при столь больших силах гравитации надо описывать уравнениями не механики Ньютона, а теории тяготения Эйнштейна. Поэтому, строго говоря, расчеты Лапласа, основанные на космической механике, неверны, а лучше сказать, неточны. Но, тем не менее, массу и размеры звезды, которая должна сжиматься и превратиться в черную дыру, он указал правильно. Это случилось потому, что в данном случае в теории тяготения Эйнштейна справедлива та же формула, что и в теории Ньютона.

Все свойства черных дыр могут быть получены только из теории тяготения Эйнштейна, которая содержится в его обшей теории относительности.

В начале нашего века, когда была создана Эйнштейном общая теория относительности, никто не был готов к ее восприятию, включая крупных ученых: слишком сильно на всех давил здравый смысл. Но прошедшие десятилетия сделали свое дело: теорию относительности изучают в средней школе, а в обыденном разговоре то и дело можно услышать: "Все в мире относительно". Так что же происходит при сильном сжатии звезды, если следовать теории относительности Эйнштейна?

При сжатии звезды (с сохранением ее массы) ее радиус уменьшается, а сила тяготения увеличивается. Это естественно. Когда радиус станет равным нулю, .сила тяготения должна стать бесконечно большой. Это следует из теории тяготения Ньютона. По теории А. Эйнштейна сила притяжения становится бесконечно большой еще до того, как радиус уменьшится до нуля. То есть она нарастает с уменьшением радиуса быстрее, чем по теории Ньютона. Тот радиус, при достижении которого сила тяготения стремится к бесконечности, принято называть гравитационным радиусом. Подчеркнем еще раз, что по классическим представлениям, он равен нулю.

Чем меньше масса тела, тем меньше его гравитационный радиус. Например, для нашей Земли он равен 1 сантиметру, для Солнца он равен 3 километрам. Различия между классической теорией и теорией относительности проявляются тогда, когда истинный радиус звезды близок к гравитационному радиусу. Пока различие между ними большое, нет необходимости привлекать теорию тяготения А. Эйнштейна, а можно спокойно пользоваться классическими уравнениями Ньютона, как это и делал П. Лаплас.

Теория относительности А. Эйнштейна устанавливает взаимоотношения между силами гравитации, течением времени и геометрическими свойствами пространства. Из нее следует, что в сильном гравитационном поле время замедляется относительно тех мест, где силы гравитации малы. Так, вблизи Земли время течет на одну миллиардную часть медленнее, чем в далеком космосе. Ясно, почему мы этого не замечаем. Даже вблизи массивных звезд это замедление времени неощутимо. Оно сразу дает о себе знать, когда масса звезды очень велика, а радиус очень мал, то есть при приближении к гравитационному радиусу. Но с силами гравитации связано не только время, но и пространство. В соответствии с теорией относительности пространство искривляется в гравитационном поле. Чем больше это поле, тем сильнее искривление. Приводится даже такое наглядное сравнение. Идеальную плоскость в пространстве делают из тонкой резиновой нервущейся пленки. На нее опускают металлический шар (черную дыру) и под его весом пленка прогибается. Так иллюстрируют искривление пространства под действием гравитационного поля массивной черной дыры. Надо сказать, что как замедление времени, так и искривление пространства вблизи сильных полей гравитации были измерены. В теории относительности существовавшие до этого по отдельности понятия абсолютного времени и абсолютного пространства объединены в одно понятие "пространство — время", поскольку они взаимосвязаны через поле гравитации.

Значение гравитационного радиуса было рассчитано по уравнениям теории тяготения Эйнштейна спустя месяц после опубликования теории в 1915 году немецким астрономом и математиком К. Шварцшильдом. С тех пор этот радиус носит его имя. Шварцшильд получил решения уравнений Ньютона для сферического не вращающегося тела и основные свойства черной дыры, хотя в то время ни он, ни А. Эйнштейн, которому он передал работу, еще не подозревали о таком приложении результатов.

Пока силы гравитации сжимают звезду и ее радиус больше радиуса Шварцшильда, силам гравитации противодействуют силы внутреннего давления звезды. Эти силы неспособны противостоять сжимающей звезду силе гравитации в том случае, если ее радиус уменьшится до гравитационного радиуса. Произойдет сжатие вещества звезды, которое физики назвали релятивистским коллапсом. Собственно, и черные дыры длительное время назывались коллапсами и только в конце шестидесятых годов с легкой руки американского физика Д. Уилера их стали называть так.

Напрашивается вывод, что если каким-либо образом сжать звезду или планету до размеров ее гравитационного радиуса, то дальше усилия можно не прилагать — она скол-лапсирует сама и превратится в черную дыру. Для этого требуется немного— сжать, например, Солнце до радиуса в 3 километра.

Строгий расчет релятивистского гравитационного коллапса на основании решения уравнений общей теории относительности был выполнен в 1939 году американскими учеными Р. Оппенгеймером и Г. Волковым. Это было строгое, теоретически обоснованное предсказание существования черной дыры. Ясно, что ни Шварцшильд, ни тем более Лаплас не предсказали существование черных дыр со всеми их свойствами.

Границей черной дыры является сфера с радиусом Шварцшильда. Чем ближе к этой границе приближается излучающее тело, тем большее влияние на него оказывают силы гравитации. И не только на него, но и на излучение. Фотоны, составляющие это излучение, уменьшают свою энергию под действием силы гравитации черной дыры. Часть их энергии уходит на противоборство с этой силой. Уменьшение энергии фотона означает уменьшение его частоты.

Другими словами, частота излучения смещается в сторону красного края спектра видимого излучения. Говорят, что излучение "краснеет". Если бы фотонам кто-то добавлял энергию, то излучение бы "голубело". Покраснение излучения, как мы уже знаем, происходит и в результате действия эффекта Доплера. Только рассматриваемое здесь красное смещение, в отличие от доплеровского, называют гравитационным. Оно обусловлено замедлением времени вблизи черной дыры под действием сил гравитации. Очень важно уловить смысл происходящего: приближающаяся к черной дыре звезда излучает такие же (белые) фотоны, что и на большом удалении от черной дыры, но удаленный наблюдатель увидит их покрасневшими, так как при движении к нему они замедляются, то есть уменьшают свою энергию. Когда звезда приблизится к границе черной дыры, далекий наблюдатель вообще перестанет ее видеть. Для него время здесь практически останавливается. Звезда для далекого наблюдателя потухает за стотысячную долю секунды. Мы упоминаем далекого наблюдателя не случайно. Часы наблюдателя, который находится на движущейся звезде, никакого замедления времени не отметят. Его нет. Оно есть только у удаленного наблюдателя, который получает всю информацию о ходе времени с помощью света, а свет его подводит, поскольку скорость фотонов замедляется, и они приходят позже обычного (когда на них не действует гравитация черной дыры).

По классической теории тяготения Ньютона одно тело, двигаясь вблизи другого, описывает разные траектории, имеющие в разных случаях форму гиперболы, параболы или эллипса. Ясно, что никаких особенностей в этом плане вблизи черной дыры из классической механики не следует. Но они следуют из теории относительности. Так, замкнутая в классическом случае эллиптическая траектория одного тела около другого становится незамкнутой, если этим другим телом является черная дыра. Пролетающее тело навивает траектории вокруг черной дыры, то приближаясь, то удаляясь от нее, но на свою старую траекторию не возвращается. Кстати, все траектории при этом располагаются в одной плоскости. Если траектория тела не подходит очень близко к черной дыре, то ее можно представить в виде поворачивающегося эллипса. Он имеется и у планет нашей Солнечной системы. Но составляет он за сто лет менее одной угловой минуты. Тем не менее он был измерен и было показано, что он точно соответствует теории относительности. Черная дыра изменяет не только траекторию движущейся вблизи нее частицы, но и ее скорость. Вблизи черной дыры частица старается двигаться быстрее. Если она попадает на удаление гравитационного радиуса, то она должна двигаться со скоростью света. Ясно, что ближе частица двигаться по кругу не может, так как для этого ей надо превысить скорость света.

Но движение тела вокруг дыры на расстояниях ближе чем три гравитационных радиуса неустойчиво, поэтому оно реально невозможно: неустойчивость приводит к возмущению дви-жения и частица сходит с круговой траектории и (или) падает внутрь черной дыры или же улетает в направлении от дыры.

Если тело летит из космоса вблизи черной дыры, то оно может быть ею захвачено. Пролетая мимо черной дыры, тело может обернуться вокруг дыры несколько раз и снова улететь в космическое пространство. Так происходит в том случае, если тело подошло близко к окружности с радиусом, который равен двум гравитационным радиусам. Но если оно село на эту окружность, то его орбита будет навиваться на нее. Это тело уже никуда от черной дыры не денется, она его гравитационно захватила. Еще более близкий подход тела к черной дыре чреват катастрофическими для него последствиями — оно упадет в черную дыру.

Движущееся вокруг черной дыры тело излучает гравитационные волны. Вообще все небесные тела при своем движении излучают гравитационные волны. Но они несут очень малую энергию, и пока что их не удается замерить. Но если тело движется вокруг черной дыры, то излученные им за это время гравитационные волны должны содержать весьма внушительную энергию (в шесть раз больше, чем при ядерном синтезе, когда в энергию превращается только один процент массы вещества).

Движение фотонов около черной дыры также непроизвольно, Они могут подступиться к дыре не ближе чем на полтора гравитационных радиуса. Но это движение фотона неустойчиво, и он может быть сбит с траектории в ту или другую сторону. Ясно, что фотоны, как и тела, будут захвачены черной дырой, если подойдут к ней очень близко (ближе полутора гравитационных радиусов). Луч будет навиваться (как на клубок) на черную дыру, если его траектория проходила вплотную к полуторному радиусу. Если он проходил еще ближе к черной дыре, то он будет упираться в черную дыру. При удалении излучения от. черной дыры происходит его покраснение, при приближении фотонов к дыре их частота (а значит, и энергия) увеличивается, и удаленный наблюдатель должен заметить поголубение света. Но для этого фотоны должны подойти очень близко к сфере Шварцщильда. Многочисленные теоретические исследования различных аспектов проблемы черных дыр позволили установить, что определяющей (и пожалуй, даже единственной) характеристикой черных дыр является их масса. В чем-то другом отличия в них нет. Можно сказать, что черные дыры с одинаковой массой являются идентичными друг другу. Что касается формы черной дыры, то было показано, что они должны быть идеально сферическими. Любое отклонение от сферичности черная дыра сбрасывает в виде излучения. Кстати, дыры сбрасывают также все возможные поля, они оставляют себе только сферическое поле тяготения, а также сферическое поле электрического заряда (в том случае, если звезда им до этого обладала). Кроме массы (это главное!) и электрического заряда черные дыры, вообще-то, характеризуются и характером их вращения. Ведь вращение определенным образом изменяет гравитационное поле дыры. В результате вращения дыры вокруг нее образуется своего рода гравитационный вихрь. Это вихревое гравитационное поле целиком определяется моментом импульса тела (равным произведению трех параметров звезды: ее радиуса, массы и скорости вращения на экваторе). Из-за вращения, создающего вихревой гравитационный вихрь, граница черной дыры несколько расширяется, она выходит за пределы сферы Шварцшильда. Сферу Шварцшильда принято называть горизонтом (за ним черная дыра, то есть уже ничего не видно). Если черная дыра вращается, то сила гравитации становится бесконечно большой еще до того, как будет достигнут горизонт. Эта граница была названа границей эргосферы. Ее принципиальное отличие от горизонта состоит в том, что из-под нее может вернуться обратно в космос попавшее туда тело. Тела в зоне между горизонтом и границей эргосферы закручиваются дырой во вращательное движение (если они не двигались первоначально супротив него), но могут с течением времени не только упасть в черную дыру, но и вылететь обратно за пределы эргосферы.

Таким образом, вращение черной дыры меняет всю картину принципиально. Границей черной дыры является ее горизонт, из-за которого ничто не возвращается. Ясно, что самая большая скорость вращения черной дыры может быть такой, при которой экваториальная линейная скорость равна скорости света.

Можно сказать, что черные дыры не представляют собой небесные тела в общепринятом смысле. Они не являются и излучением. Это действительно дыры во времени и пространстве, которые образуются в результате того, что в сильно увеличивающемся гравитационном поле очень сильно искривляется пространство и изменяется характер течения времени.

Возникает естественный вопрос: как обнаружить черную дыру? Теоретики предположили, как им казалось, много таких возможностей, но на их проверку труд экспериментаторов был потерян безрезультатно. На сегодняшний день реализовалась одна из этих возможностей. Суть ее состоит в том, что черную дыру следует искать в двойных звездных системах. Она должна выдать себя по рентгеновскому излучению, которое должно неизбежно возникать при падении газа из атмосферы "нормальной" звезды. Этот газ должен закручиваться за счет движения звезд по орбите и одновременно сплющиваться в диск под де