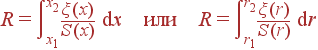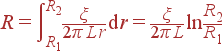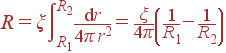Скачать

Утечка заряда в конденсаторах

М.И. Векслер, Г.Г. Зегря

Диэлектрик в конденсаторе обладает конечным удельным (Ом·см) сопротивлением ξ, которое может зависеть от координат. Ток через конденсатор при U0 = const составляет

I = \frac{U_0}{R}

(46)

где в случае ξ = ξ(x) или ξ = ξ(r)

R=\int\limits_{x_1}^{x_2} \frac{\xi(x)}{S(x)} {\rm d}x {\rm или} R = \int\limits_{r_1}^{r_2} \frac{\xi(r)}{S(r)} {\rm d}r

(47)

S(x) (или S(r)) обозначает площадь эквипотенциальной поверхности. Если батарею отключить, то напряжение на конденсаторе будет спадать по закону

-C \frac{{\rm d}U}{{\rm d}t} = I(t) = \frac{U(t)}{R}

(48)

где C - емкость. Отсюда получаем

U(t) = U_0\cdot \exp\left(-\frac{t}{RC}\right)

(49)

Задача. Найти сопротивление R цилиндрического конденсатора (R1, R2, L, ξ = сonst).

Решение: Эквипотенциальные поверхности - это боковые цилиндрические поверхности, площадь каждой из которых

S = 2π L r

Поскольку ξ = const, по формуле для сопротивления получаем:

R = \int\limits_{R_1}^{R_2}\frac{\xi}{2\pi L r} {\rm d}r = \frac{\xi}{2\pi L} \ln\frac{R_2}{R_1}

Задача: Напряжение на сферическом конденсаторе емкости C (R1, R2) после отсоединения его от батареи спало в η раз за время Δ t. Найти удельное сопротивление диэлектрика (диэлектрик считать однородным).

Решение: Омическое сопротивление описанного конденсатора равно

R = \xi \int\limits_{R_1}^{R_2} \frac{{\rm d}r} {4\pi r^2} = \frac{\xi}{4\pi}\left(\frac{1}{R_1}-\frac{1}{R_2} \right)

где ξ - искомое удельное сопротивление.

Если t = 0 соответствует моменту отсоединения батареи, то, как следует из условия, напряжение на конденсаторе в момент t = Δ t составляет U0/η (U0 - начальное напряжение):

U(\Delta t) = \frac{U_0}{\eta} = U_0\cdot\exp \left(-\frac{\Delta t}{RC}\right)

откуда получается

R = \frac{\Delta t}{C\ln\eta}

Приравнивая это R и выражение для того же R через ξ, имеем

\xi = \frac{4\pi \Delta t}{C\ln\eta}\left(\frac{1} {R_1}-\frac{1}{R_2}\right)^{-1}

Задача: Напряжение на цилиндрическом конденсаторе с радиусами обкладок R1, R2 и длиной L спало в η раз за время Δ t после отсоединения конденсатора от батареи. Найти удельное сопротивление диэлектрика (диэлектрик однороден и имеет проницаемость ε).

Ответ: \xi = \frac{\Delta t}{\varepsilon_0\varepsilon \ln\eta} (нет зависимости от R1, R2, L).

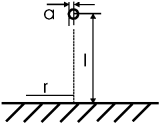
Задача. В диэлектрике проницаемости ε на расстоянии l от бесконечной проводящей плоскости расположен небольшой металлический шарик радиуса a<< l. Найти ток, если между шариком и плоскостью поддерживается разность потенциалов U, а удельное сопротивление среды ξ.


Категории:

Подобное:

Copyright © https://referat-web.com/. All Rights Reserved