Тождественные преобразования алгебраических выражений
Карпова Ирина Викторовна, старший преподаватель кафедры алгебры ХГПУ
1. Алгебраическим выражением называется выражение, составленное из конечного числа букв и чисел, соединенных знаками действий сложения, вычитания, умножения, деления, возведения в целую степень и извлечение корня.
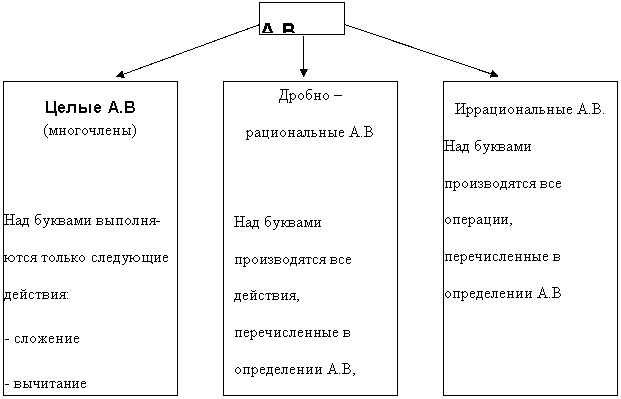 |
Все алгебраические выражения (А.В) по действиям, которые производятся над буквами можно классифицировать следующим образом:
Буквы, входящие в А.В могут принимать значения из некоторого числового множества, которое называется множеством допустимых значений или областью определения А.В.
Так, в рассмотренных выше примерах 1) и 2) значениями букв, входящих в А.В могут быть любые числа. В общем случае область определения (О.О.) целых алгебраических выражений может быть любым числовым множеством.
Так как делить на выражение равное нулю нельзя, то с и b в пр.3) могут принимать любые числовые значения, кроме с=0 и b=0, таким образом О.О. А.В из пр.3) с¹0, b¹0. На этом же основании О.О. А.В из пр.4) x+y¹0 или х¹y.
В общем случае О.О. дробно-рационального А.В не включает те значения, входящих в выражение букв, при которых знаменатель дробей в выражении обращается в нуль.
Область определения А.В из пр.5) а¹b, b¹0 и а>0 т.к. выражение стоящее под знаком корня четной степени должно быть, по определению арифметического корня, неотрицательным.
О.О. А.В из пр.6) х+1³0 или х³-1.
В общем случае О.О. иррационального выражения включает только те значения букв, при которых выражения, стоящие под знаком корня четной степени принимают неотрицательные значения.
Тождеством называется равенство двух А.В справедливое для любых допустимых значений, входящих в него букв.
Равенство (a+b)2=a2+2ab+b2 справедливое для любых a и b есть тождество.
Равенство ![]() является тождеством только для а¹1.
является тождеством только для а¹1.
Тождественным преобразованием А.В называется замена одного А.В другим тождественно ему равным, но отличным по форме.
a3+3a2b=a2(a+3b)
![]() при с¹0.
при с¹0.
Целью тождественных преобразований (Т.П) может быть приведение выражению вида, более удобного для численных расчетов или дальнейших преобразований.
К Т.П относятся:
приведение подобных членов
раскрытие скобок
разложение на множители
приведение алгебраических дробей к общему знаменателю
избавление от иррациональности в знаменателе и т.п.
2. Рассмотрим тождественные преобразования А.В.
Для успешного осуществления Т.П. целых А.В нужно помнить:
Формулы сокращенного умножения
(a ± b)2 = a2 + 2ab + b2
a3 ± b3 = (a ± b)( a2![]() ab+b2)
ab+b2)
(a ± b)3 = a3 ± 3a2b + 3ab2 ± b3
a2 – b2 = (a + b)(a – b)
Свойства степени с целыми показателями
![]()
![]()
![]()
![]()
![]()
Формулы корней квадратного трехчлена ax2 + bx + c
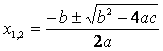
Теорему Виета х1 и х2 — корни ax2 + bx + c в том и только том случае, если
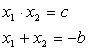
Разложение квадратного трехчлена ax2 + bx + c на множители.
Если х1, х2 — корни трехчлена, то ax2 + bx + c = а(х–х1)(х–х2)
Рассмотрим несколько примеров тождественных преобразований целых А.В.
Пример 1. Разложить многочлен на множители ![]()
Решение:
Задача заключается в том, чтобы сгруппировать слагаемые так, чтобы они имели общий множитель, который можно будет затем вынести за скобки, прейдя от суммы к произведению.
Итак.
Объединим крайние слагаемые в одну группу, а средние в другую: ![]()
2) Вынесем за скобки во второй группе общий множитель 2ab, получим: ![]()
3) Вынесем за скобки общий множитель первого и второго слагаемого (a2 + b2):
![]()
Полученное выражение есть произведение двух сомножителей, а значит многочлен f(a,b) разложили на множители.
Ответ: ![]()
Пример 2. Разложить на множители f(a)= a3 – 7а2 + 7а +15
Решение:
Как бы мы не группировали слагаемые мы не получим группы слагаемых, имеющие одинаковые множители. Поэтому, сначала преобразуем сами слагаемые.
–7а2 = –3а2 – 4а2
7а = 12а – 5а
f (a) = a3 – 7а2 + 7а +15 = a3 – 3а2 – 4а2 + 12а – 5а +15
3) Сгруппируем слагаемые попарно, и из каждой скобки вынесем общий множитель.
f(a) = (a3 – 3а2) +( – 4а2 +12а) + (– 5а +15) = а2 (а – 3) – 4а (а – 3) – 5(а – 3)
4) В полученном выражении все слагаемые имеют общий множитель (а – 3), который и выносим за скобки. f(a) = (а – 3)(а2 – 4а – 5)
5) Мы получили разложение на множители f(a), но второй множитель в свою очередь может быть разложен на множители. Для этого, используя теорему Виета, разложим трехчлен (а2 – 4а – 5) на множители.
По теореме Виета корнями трехчлена (а2 – 4а – 5) являются а1=5 и а2= –1. Тогда имеем (а2 – 4а – 5) = (а – 5)(а + 1) и f(a) = (а – 3)(а – 5)(а + 1)
Ответ: a3 – 7а2 + 7а +15 = (а – 3)(а – 5)(а + 1).
Пример 3. Разложить на множители f(a,b,c) = ab(a+b) – bc(b+c) + ac(a – c).
Решение:
1) Заметим, что выражение, стоящее в первых скобках есть сумма выражений, стоящих во второй и в третьей скобках a+b=(b+c)+(a–c). Подставим это вместо а+b.
f(a,b,c)=ab((b+c)+(a–c))–bc(b+c)+ac(a–c)=ab(b+c) + ab(a–c)–bc(b+c)+ac(a–c)
2) Сгруппируем 1-е и 3-е слагаемые и 2-е и 4-е и вынесем общие множители за скобки.
f(a,b,c)=(b+c)(ab–bc)+(a–c)(ab–ac)=(b+c)(a–c)b+(a–c)(b+c)a=(a–c)(b+c)(b+a)
Полученное есть произведение трех сомножителей.
Ответ: ab(a+b) – bc(b+c) + ac(a – c)=(a–c)(b+c)(b+a).
Пример 4. Разложить на множители f(a,b)=4a2–12ab+5b2.
Решение:
1) Выделим полный квадрат
f(a,b)=(2a)2–2(2a)(3b)+(3b)2 –4b2 =(2a–3b)2 –4b2.
2) Воспользуемся формулой разности квадратов:
f(a,b)=((2a–3b)–2b)((2a–3b)+2b)=(2a–5b)(2a–b).
Ответ: 4a2–12ab+5b2=(2a–5b)(2a–b).
Пример 5. Разложить на множители f(a)=а3+9а2+27а+19.
Решение:
Так как выражение зависит только от а, которое входит в выражение в 3-ей, 2-ой и 1-ой степенях, попытаемся выделить полный куб, воспользуясь формулой (a+b)3=a3+3a2b+3ab2+b3.
1) f(a)=a3+3a2 ×3+3a×32+33 –8
2) т.к. 8=23, то воспользуемся формулой разности кубов: a3 –b3=(a–b)(a2+ab+b2).
f(a)=(a+3)3–23=(a+3–2)((a+3)2+2(a+3)+22)=(a+1)(a2+8a+19).
Ответ: а3+9а2+27а+19=(a+1)(a2+8a+19).
3. Рассмотрим примеры тождественных преобразований дробно-рациональных выражений.
При выполнении Т.П. таких выражений надо следить за областью определения выражения, т.к. может происходить расширение области определения. Это может произойти, например, при сокращении дроби.
Так область определения дроби![]() все х¹1 и х¹ –2.
все х¹1 и х¹ –2.
Вместе с тем ![]() .
.
Сократив дробь, получим ![]() . Область определения полученной дроби: х¹-2, т.е шире, чем О.О. первоначальной дроби.
. Область определения полученной дроби: х¹-2, т.е шире, чем О.О. первоначальной дроби.
Поэтому дроби ![]() и
и ![]() равны при х¹1 и х¹-2.
равны при х¹1 и х¹-2.
Изменение области определения выражения возможно и в результате некоторых других преобразований, поэтому, выполнив преобразования выражения, нужно всегда уметь ответить на вопрос, на каком множестве оно тождественно полученному.
Пример 1. Сократить дробь ![]()
Решение:
1) Найдем О.О. Для этого нужно потребовать, чтобы знаменатель дроби был отличен от 0. a+b¹0 Þ a¹b. Таким образом О.О. f(a) все a¹b.
2) Чтобы сократить дробь, разложим числитель на множители
2а2+ab-b2=2a2+2ab-ab-b2=(2a2+2ab)+(-ab-b2)=2a(a+b)-b(a+b)=(a+b)(2a-b)
3) ![]()
Ответ: ![]() .
.
Пример 2. Упростить выражение
![]()
Решение:
Найдем область определения: а2+3а+2¹0, а2+4а+3¹0, а2+5а+6¹0.
Используя т. Виета найдем значения а, при которых трехчлены обращаются в нуль
а2+3а+2=0 при а1=–2, а2=–1
а2+4а+3=0 при а1=–3, а2=–1
а2+5а+6=0 при а1=–3, а2=–2
таким образом область определения f(а): а¹–2, а¹–1, а¹–3
Приведем сумму дробей, стоящую в скобках, к общему знаменателю, предварительно определив его, используя 1)
а2+3а+2=(а+2)(а+1)
а2+4а+3=(а+3)(а+1)
а2+5а+6=(а+3)(а+2) тогда общий знаменатель: (а+2)(а+3)(а+1).
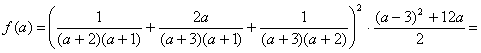
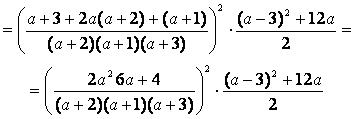
Разложим числитель первой и второй дроби на множители:
2а2+6а+4=2(а2+3а+2)=2(а+2)(а+1)
(а–3)2+12а=а2–6а+9+12а=а2+6а+9=(а+3)2
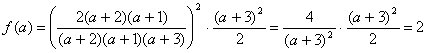
Ответ: ![]()
при а¹–3, а¹–2, а¹–1.
Пример 3. Упростить выражение 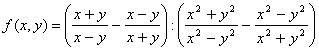
Решение:
Найдем область определения:
х–у¹0 Þ х¹у
х+у¹0 Þ х¹–у
х2–у2¹0 Þ х¹у, х¹–у
х2+у2¹0 Þ х¹0, у¹0.
Итак, область определения х¹0, у¹0, х¹у, х¹–у.
Приведем дроби, стоящие в скобках к общему знаменателю и воспользуемся формулами сокращенного умножения
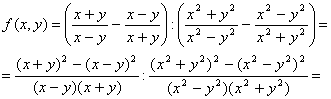
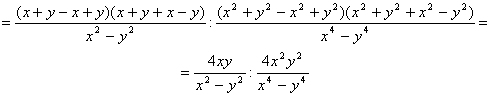
Воспользуемся правилом деления дробей: ![]()
![]()
Ответ: ![]() при х¹0, у¹0, х¹у, х¹–у.
при х¹0, у¹0, х¹у, х¹–у.
Пример 4. Упростить выражение

Найдем область определения выражения:
а¹0 Þ
b+с¹0 Þ b¹–с
![]() Þ b+с–а¹0 Þ b+с¹а
Þ b+с–а¹0 Þ b+с¹а
а¹0 и b+с¹0
2bс¹0 Þ b¹0, с¹0.
Таким образом, область определения: а¹0, b¹0, с¹0, b¹–с, b+с¹а.
Приведем дроби, стоящие в числителе и знаменателе первой дроби, а также сумму, стоящую в скобках, к общим знаменателям
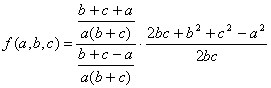
Воспользуемся правилом деления дробей и приведем четырехэтажную дробь к двухэтажной. В числителе второй дроби выделим полный квадрат суммы b и с
![]()
Числитель второй дроби, воспользовавшись формулой разности квадратов, разложим на множители
![]()
Ответ: ![]() при а¹0, b¹0, b¹–с, с¹0, b+с¹а.
при а¹0, b¹0, b¹–с, с¹0, b+с¹а.
Пример 5. Упростить выражение![]()
Найдем область определения выражения, для этого потребуем
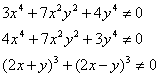
первые два выражения, как сумма трех неотрицательных слагаемых равны нулю только при х=0 и у=0.
Рассмотрим третье выражение
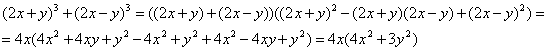
тогда ![]() когда
когда ![]() . Отсюда имеем х¹0, у¹0.
. Отсюда имеем х¹0, у¹0.
Т.о. обл. определения х¹0, у¹0.
2) Знаменатель третьей дроби мы заложили на множители, находя область определения выражения. Разложим на множители числитель первой дроби, а в числителе и в знаменателе второй представим
![]()

Воспользуемся правилами деления дробей
![]()
Ответ: ![]()
Пример 6. Упростить выражение ![]()
Решение:
Найдем область определения:
b-c ¹ 0 Þ b ¹ c
c-a ¹ 0 Þ c ¹ a
a-b ¹ 0 Þ a ¹ b
2) Приведем дроби к общему знаменателю (b-c)(c-a)(a-b)
![]()
3) Воспользуемся формулами сокращенного умножения
![]()
Ответ: f(a,b,c) = 0 при b ¹ c, c ¹ a, a ¹ b.
4. Для успешного выполнения тождественных преобразований иррациональных выражений нужно помнить:
1. Определение арифметического корня n-ой степени:
Если ![]() и n – натуральное число большее 1, то существует только одно неотрицательное число x такое, что выполняется равенство
и n – натуральное число большее 1, то существует только одно неотрицательное число x такое, что выполняется равенство ![]() . Это число х называется арифметическим корнем n-ой степени из неотрицательного числа а и обозначается
. Это число х называется арифметическим корнем n-ой степени из неотрицательного числа а и обозначается ![]() .
.
Пример.

Если n – нечетное натуральное число большее 1 и а < 0, то под ![]() понимают такое отрицательное число х, что
понимают такое отрицательное число х, что ![]() .
.
Пример. ![]()
2. Из определения 1. Следует, что если в алгебраическом выражении есть корни четной степени, то подкоренные выражения таких корней должны быть неотрицательными, что учитывается при определении области определения алгебраического выражения.
Пример. ![]()
Область определения выражения ![]()
3. Определение модуля числа.
Модулем числа а называется само число а, если ![]() и противоположное ему число, если а < 0 т.е.
и противоположное ему число, если а < 0 т.е. ![]()
4. Свойства арифметического корня:
Если n, k, m – натуральные числа, ![]() то:
то:
1° ![]()
2° 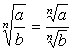 , если b ¹ 0.
, если b ¹ 0.
Замечание. Если a < 0, b < 0, то свойства 1° и 2° принимают вид
![]()
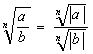
3° ![]()
4° ![]()
5° ![]()
6° ![]()
Замечание. Если показатели корней нечетные числа, то свойства 1°– 6° выполняются для a < 0, b < 0 и ab < 0.
7° Если n – четное число т.е. n = 2k, то ![]()
Пример. ![]() т.к.
т.к. ![]() , то
, то ![]() , тогда по определению модуля
, тогда по определению модуля ![]() и
и ![]() .
.
Пример 1. Упростить выражение: ![]()
Решение.
1) Сначала, используя свойства арифметического корня, упростить каждый из имеющихся радикалов:
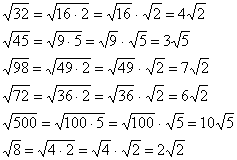
2) 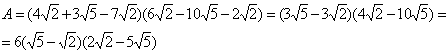
3) Раскроем скобки и приведем подобные
![]()
Ответ: ![]()
Пример 2. Упростить выражение ![]()
Решение: Выражение упростится, если окажется, что под этим корнем содержится полный квадрат разности или суммы каких-нибудь чисел.
Представим ![]() в виде полного квадрата. Для этого представим
в виде полного квадрата. Для этого представим
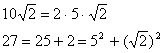 тогда
тогда ![]()
2) ![]()
3) По свойству 7° имеем ![]()
Т.к. ![]() , то
, то ![]() , тогда по определению модуля
, тогда по определению модуля
![]() и
и ![]()
Ответ: ![]() .
.
Пример 3. Освободиться от иррациональности в знаменателе дроби![]() .
.
Решение:
В знаменателе имеем иррациональность 2-ой степени, поэтому домножим и числитель, и знаменатель дроби на сумму чисел ![]() и
и ![]() , тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
, тогда в знаменателе будем иметь разность квадратов, которая и ликвидирует иррациональность.
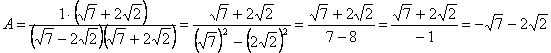
Ответ: ![]() .
.
Пример 4. Освободиться от иррациональности в знаменателе дроби
![]()
Решение:
Имеем иррациональность 3-ей степени, поэтому и числитель, и знаменатель умножим на неполный квадрат чисел ![]() и 1, тогда в знаменателе получим разность кубов, которая и ликвидирует иррациональность.
и 1, тогда в знаменателе получим разность кубов, которая и ликвидирует иррациональность.

Ответ: ![]()
Пример 5. Упростить выражения
![]()
Решение:
Воспользуемся свойствами степени с рациональным показателем и арифметического корня
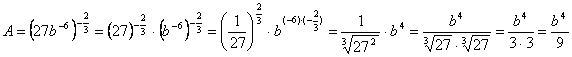
Ответ: ![]() .
.
![]()
Решение:
От десятичных дробей в показателе степени перейдем к обыкновенным и воспользуемся свойствами арифметического корня и степени с рациональным показателем
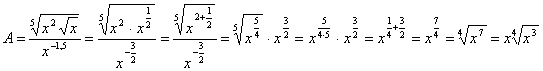
Ответ: ![]() .
.
Пример 6. Упростить выражение 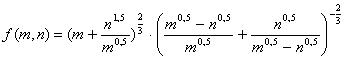
Решение:
1. Найдем область определения алгебраического выражения
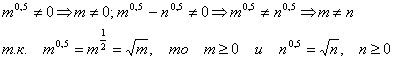
в результате имеем ![]() .
.
2. Перейдем в показателях степеней от десятичных дробей к обыкновенным и выражения, стоящие в скобках приведем к общему знаменателю

3. Числитель первой дроби преобразуем как сумму кубов
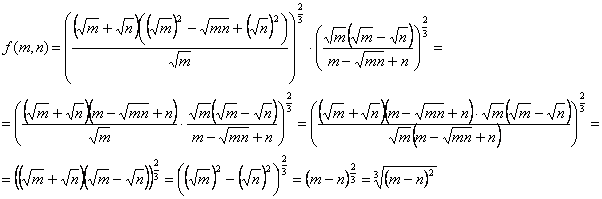
Пример 6. Упростить выражение ![]()
Решение:
Приведем дроби, стоящие под знаками корня к общему знаменателю
![]()
В числителе первой дроби стоит полный квадрат суммы, а в числителе второй дроби – полный квадрат разности ![]() и
и ![]() :
: 
3. Воспользуемся свойством арифметического корня
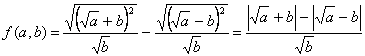
4. Так как ![]() и
и ![]() , то
, то ![]() , а значит
, а значит ![]() .
.
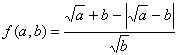
5. Так как ![]() может быть как отрицательным, так и положительным, рассмотрим два случая:
может быть как отрицательным, так и положительным, рассмотрим два случая:
1) ![]() , тогда
, тогда ![]() . В этом случае
. В этом случае ![]() и
и
![]()
2) ![]() , тогда
, тогда ![]() .
.
В этом случае ![]() и
и
![]()
Ответ: 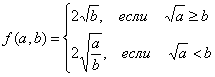 .
.
Контрольное задание.
Предлагаем для самостоятельного решения приведенные ниже задачи. Желательно решить все задачи, однако, если это не удалось, присылайте только те, которые решены.Правила оформления работ смотрите во вступительной статье.
Разложить на множители
М8.1.1. ![]()
М8.1.2. ![]()
М8.1.3. ![]()
М8.1.4. ![]()
Сократить дробь
М8.1.5. ![]()
М8.1.6. ![]()
Упростить выражение
М8.1.7. 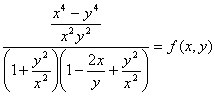
М8.1.8. 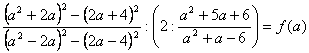
М8.1.9. ![]()
М8.1.10. Избавиться от иррациональности в знаменателе дроби ![]()
Упростить выражение
М8.1.11. ![]()
М8.1.12. ![]()
М8.1.13. 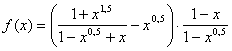
М8.1.14. 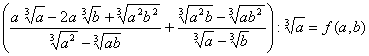
М8.1.15. 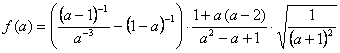
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- Был ли прав Коперник?
ВведениеГелиоцентрическая система Коперника с современной точки зрения является, несомненно, устаревшей.Во-первых, бросается в глаза о
- Алгебраические расширения полей
- Расчет площади сложной фигуры с помощью метода имитационного моделирования
Задание: Разработать программу, позволяющую с помощью метода имитационного моделирования рассчитать площадь сложной фигуры, ограничен
- Проективная геометрия
Проективная геометрия развилась и выделилась в особую ветвь геометрических знаний в первые десятилетия 19 века. Источником этого явилис
- Оптика
Работу выполнила Балтина Елена, 9 «А» класс Министерство общего и профессионального образования Свердловской обл.Управление и образова
- Планета Земля
- Вопросы к гос. экзамену по дисциплине "Математика – Алгебра"
Вопрос 3. Определитель квадратной матрицы.В вопросе рассматривается одна из характеристик матрицы - числовая. Все свойства определителя
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

