Типовой алгоритм синтеза комбинированной системы автоматического управления
Курсовая работа
Тема: "Типовой алгоритм синтеза комбинированной САУ"
Промышленные объекты управления (ОУ), как правило, представляют собой сложные агрегаты со многими входными и выходными величинами, характеризующими технологический процесс. Зависимости выходных величин от входных, как правило, нелинейные, и изменение одной из них приводит к изменению других. Таким образом, создается сложная система взаимозависимостей, которую трудно, а подчас и невозможно строго математически описать.
Большинство промышленных объектов описываются передаточными функциями, имеющими большое время запаздывания τа и большие постоянные времени Та.
Известно, что чем больше время запаздывания, тем труднее управлять объектом. Качество регулирования в будущей САУ зависит от отношения τа/ Та. Чем оно больше, тем труднее управлять, поэтому при описании объекта (τа/ Та)≤1.
Для большинства объектов τа/ Та так велико, что удовлетворяющее нас качество в системе в одноконтурной САУ получить практически невозможно. В этом случае нужно усложнить закон регулирования. На практике идут не на усложнение закона регулирования, а на усложнение структуры САУ.
В настоящее время в практике автоматизации непрерывных производственных процессов применяются следующие виды многоконтурных схем: каскадные системы, комбинированные САУ и многосвязные системы. Расчет оптимальных параметров управляющих устройств перечисленных многоконтурных систем является довольно сложной задачей. Для упрощения на практике определяют лишь приближенные значения этих параметров.
Методика приближенных расчетов основана на предположении о возможности расчета отдельных контуров системы независимо друг от друга. Для этих целей, исходная структурная схема управления подвергается различным структурным преобразованиям с тем, чтобы выделить отдельные контуры с различными частотами и рассчитывать их обычными методами независимо друг от друга, тем самым получают более сложный алгоритм управления комбинацией ограниченного числа типовых П -, ПИ-, ПИД законов регулирования.
Комбинированные системы регулирования рекомендуется строить, если на систему действуют значительные внешние возмущения и если представляется возможность выделить и измерить главные из них.
Система содержит минимум два контура регулирования. Разомкнутый контур с преобразователем ![]() служит для компенсации основного возмущения (или возмущений) f; замкнутый контур с регулятором
служит для компенсации основного возмущения (или возмущений) f; замкнутый контур с регулятором ![]() окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комбинированное управление сочетает в себе два принципа регулирования: регулирование «по возмущению» и регулирование «по отклонению».
окончательно корректирует процесс, отрабатывая ошибки компенсации первого контура и другие неучтенные возмущения, многие из которых практически не могут быть контролируемыми (помехи). Комбинированное управление сочетает в себе два принципа регулирования: регулирование «по возмущению» и регулирование «по отклонению».
1. Получение математической модели ОУ в форме передаточных функций по управляющему и возмущающему каналам
1.1 Аппроксимация переходной характеристики объекта по управляющему каналу
Экспериментальным точкам строится экспериментальная характеристика переходного процесса. Исследуемый объект – двухканальный (канал: u-y и канал: f-y) по каналу регулирования (u-y) является объектом с самовыравниванием (рис. 2). Объекты с самовыравниванием аппроксимируют передаточными функциями с введением звена запаздывания.
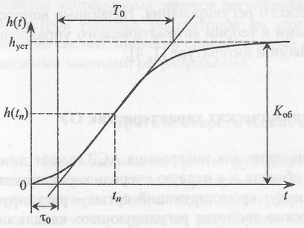
Рис. 2. Переходная характеристика ОУ с самовыравниванием
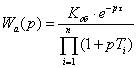 , (1.1)
, (1.1)
автоматический управление аппроксимация канал
где:
Коб – коэффициент передачи;
t – время запаздывания;
То – постоянная времени.
Простейшим частным случаем оператора (1.1), имеющим в инженерной практике наибольшее применение, является передаточная функция вида:
![]() . (1.2)
. (1.2)
Для определения параметров объекта по управляющему каналу проведём касательную к экспериментальной переходной характеристике в точке перегиба, которая имеет координатами (tп; h(tп)). Далее определяем параметры передаточной функции по управляющему каналу (приложение 1):
Коб = hуст = 0,55; tо = 1,9с; То = 10,5с; h(tп) = 0,12; tп = 4с
![]()
Подставляя эти параметры в формулу (1.2), получаем первую математическую модель ОУ:
![]()
![]()
Более точную аппроксимацию переходной функции ОУ дает передаточная функция вида:
![]() (1.3)
(1.3)
Её оригинал имеет вид:
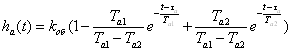 (1.4)
(1.4)
Задача математического описания в этом случае заключается в поиске таких Та1, Та2 и ![]() , при которых кривая (1.4) максимально приближается к истинной экспериментальной кривой. Записывая аналитические выражения критерия приближения, получаем уравнения для выбора этих параметров. Для упрощения расчётов, в литературе предложена номограмма:
, при которых кривая (1.4) максимально приближается к истинной экспериментальной кривой. Записывая аналитические выражения критерия приближения, получаем уравнения для выбора этих параметров. Для упрощения расчётов, в литературе предложена номограмма:
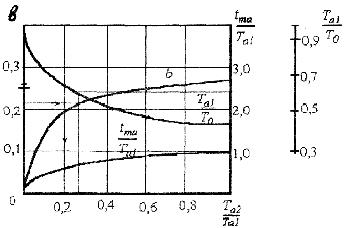
Рис. 3. Номограмма для определения параметров передаточных функций
По номограмме (рис. 3.) можно найти ![]() ,
, ![]() по известным
по известным ![]() и
и ![]() . По известному значению
. По известному значению ![]() находим значение
находим значение ![]() , после чего определяем
, после чего определяем ![]() ,
, ![]() и, следовательно:
и, следовательно:
![]()
![]()
![]()
![]()
Подставляя рассчитанные значения в формулу (1.3), получаем вторую математическую модель ОУ:
![]()
Третью модель определяем по методу Лукаса:
![]() ,
,
где ![]() ;
;
![]()
Таким образом, получили третью математическую модель ОУ:
![]()
Далее с помощью программы «СС» на ЭВМ строим переходные процессы полученных функций и наносим их на график с экспериментальной характеристикой (приложение 1).
Вычислим погрешности аппроксимации полученных передаточных функций по интегральному критерию по формуле:
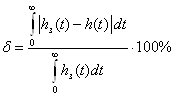
где:
![]() - аппроксимирующая переходная характеристика;
- аппроксимирующая переходная характеристика;
![]() - заданная переходная характеристика.
- заданная переходная характеристика.
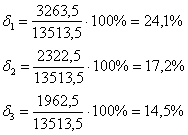
Выбираем передаточную функцию, имеющую наименьшую погрешность аппроксимации:
![]() (1.5)
(1.5)
1.2 Аппроксимация переходной характеристики объекта по возмущающему каналу
Исследуемый объект по возмущающему каналу также является объектом с самовыравниванием (рис. 2.). Поэтому первая аппроксимирующая передаточная функция примет форму оператора (1.1).
Проведём касательную к экспериментальной переходной характеристике в точке перегиба с координатами (tп; h(tп)) (приложение 2.). Определим параметры передаточной функции:
Коб = hуст = 0,28; tо = 3,1с; То = 9с; h(tп) = 0,06; tп = 5с
![]()
Получили передаточную функцию первой модели для возмущающего канала:
![]()
Далее для нахождения передаточной функции второй модели (1.3) как и в предыдущем пункте по номограмме (рис. 3) находим:
![]()
![]()
![]()
![]()
Подставляя рассчитанные значения в формулу (1.3), получаем вторую математическую модель ОУ:
![]()
Для нахождения передаточной функции по методу Лукаса определяем следующие коэффициенты:
![]() ;
;
![]()
Таким образом, получили третью передаточную функцию для возмущающего канала:
![]()
Находим погрешности аппроксимации по интегральному критерию:
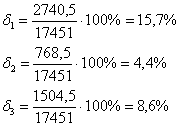
Выше представленные расчёты показывают, что наименьшую погрешность аппроксимации даёт третья модель, следовательно, она наилучшим образом аппроксимирует экспериментальную характеристику.
![]()
2. Выбор ПИ-алгоритма управления
В качестве показателя оптимальности АСР принимается минимум интеграла от квадрата ошибки системы при действии на объект наиболее тяжелого ступенчатого возмущения по регулирующему каналу (интегральный квадратичный критерий) с учетом добавочного ограничения на запас устойчивости системы, т.е.
![]() . (2.1)
. (2.1)
Такой критерий допускает значительное перерегулирование ![]() и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины.
и увеличивает время регулирования, но он обеспечивает наименьшее максимальное динамическое отклонение регулируемой величины.
При практических расчётах запас устойчивости удобно характеризовать показателем колебательность системы М, значение которого в САУ, имеющих интеграл в алгоритме управления, совпадает с максимумом амплитудно-частотной характеристики системы:
![]() (2.2)
(2.2)
где:
wр – резонансная частота, на которой Аз() имеет максимум.
Чтобы максимум не превышал некоторой заданной величины М, амплитудно-фазовая характеристика (АФХ) разомкнутой системы Wраз(j) не должна заходить внутрь «запретной» области ограниченной окружностью, центр uo и радиус Ro которой определяется через М формулами (2.3) и (2.4), (рис. 4):
![]() (2.3)
(2.3)
![]() . (2.4)
. (2.4)
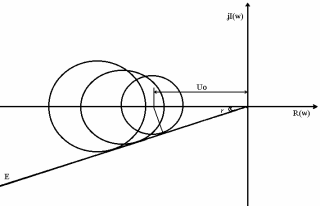
Рис. 4. Определение центра и радиуса окружности, соответствующей заданному показателю колебательности М
Если же Wраз(j) касается указанной окружности, то это означает, что САУ находится на границе заданного запаса устойчивости.
На практике чаще всего принимают ![]() . При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.
. При этом в САУ перерегулирование g £ 30%, максимальное отклонение регулируемого параметра при внутренних возмущениях (возмущениях по регулирующему воздействию) не превышает 10%.
С помощью программы «СС» рассчитываем и строим АФХ объекта по передаточной функции (1.5) (приложение 3). Результаты расчёта приведены в таблице 2:
Таблица 2
| 0 | 0,042 | 0,082 | 0,131 | 0,192 | 0,255 | 0,339 | 0,451 | 0,599 | 0,797 |
| А | 0,55 | 0,536 | 0,5 | 0,44 | 35 | 0,279 | 0,2 | 0,136 | 0,086 | 0,052 |
| 0 | -20 | -38,7 | -60 | -81,7 | -100,6 | -120,5 | -140,4 | -160 | -179,6 |
| 0,797 | 1,06 | 1,409 | 2,059 | 3,009 |
| ||||
| А | 0,052 | 0,031 | 0,018 | 0,009 | 0,004 |
| ||||
| -179,6 | -199,7 | -222 | -256,9 | -300,7 |
| ||||
Категории:
- Астрономии
- Банковскому делу
- ОБЖ
- Биологии
- Бухучету и аудиту
- Военному делу
- Географии
- Праву
- Гражданскому праву
- Иностранным языкам
- Истории
- Коммуникации и связи
- Информатике
- Культурологии
- Литературе
- Маркетингу
- Математике
- Медицине
- Международным отношениям
- Менеджменту
- Педагогике
- Политологии
- Психологии
- Радиоэлектронике
- Религии и мифологии
- Сельскому хозяйству
- Социологии
- Строительству
- Технике
- Транспорту
- Туризму
- Физике
- Физкультуре
- Философии
- Химии
- Экологии
- Экономике
- Кулинарии
Подобное:
- IP-телефония. Особенности цифровой офисной связи
Тема«IP-телефония. Особенности цифровой офисной связи»Группа: МО – 41Студентка: Латыпова Г.СIP-телефонияЧто такое IP-телефония?IP-телефония
- Дисперсия в волоконных световодах
- Історія зв’язку та його розвиток
Історія зв’язку та його розвитокЩе в стародавні століття виникла необхідність передавати різні повідомлення (інформацію) на відстань
- Контроль характеристик термоперетворювачів опору
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИНаціональний університет «Львівська політехніка»Інститут Комп’ютерних технологій, автоматики і
- Методика проектування пристроїв синхронізації
СодержаниеВступ1. Методика проектування пристроїв синхронізації1.1 Будова інформаційної моделі1.2 Вибір алгоритму пошуку1.3 Визначення
- Напрямки розвитку волоконної оптики
- Нелинейные эффекты вынужденного неупругого рассеивания световой волны в волокне
Нелинейные эффекты вынужденного неупругого рассеивания световой волны в волокнеВынужденное рассеивание Бриллюэна (SBS – StimulatedBrillouinScatte
Copyright © https://www.referat-web.com/. All Rights Reserved
 referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.

