referat-web.com Бесплатно скачать - рефераты, курсовые, контрольные. Большая база работ.
Теоретический анализ модели комплексного числа
Введение.
§1. Система комплексных чисел
§2. Свойства комплексных чисел
§3. Полем комплексных чисел.
§4. Категоричность аксиоматической теории комплексных чисел.
§5. Непротиворечивость аксиоматической теории комплексных чисел
§6. Модели комплексных чисел.
Примеры.
Заключение
Список используемой литературы
Из курса математики известно, что отрицательные числа введены прежде всего для того, чтобы операция вычитания, обратная к операции сложения, была всегда возможна. По аналогичной причине в математике появились комплексные числа. Если рассматривать только действительные числа, то операция извлечения квадратного корня, обратная к операции возведения в квадрат, не всегда возможна, так как нельзя извлечь квадратный корень из отрицательного числа. Этого, однако, недостаточно, чтобы заводить в математике новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречается корень квадратный из отрицательного числа, то можно прийти к результату, уже не содержащему корень квадратный из отрицательного числа. В XVI веке Кардано нашел формулу для решения кубического уравнения. Оказалось, что именно в том случае, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается корень квадратный из отрицательного числа. Обнаружилось таким образом, что производя вычисления с выражениями, содержащими корень квадратный из отрицательного числа, можно получить вполне понятные результаты. Поэтому эти корни стали употреблять в математике. Назвали их мнимыми числами — тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам на грани XVIII—XIX столетий дал Гаусс, который назвал их комплексными числами, дал им геометрическую интерпретацию и, что самое главное, доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный или комплексный корень. Комплексным числом называется всякая упорядоченная пара действительных чисел 
. Два комплексных числа и 
равны тогда и только тогда, когда 
. Рассмотрим комплексны числа более подробно. И найдем модели комплексных чисел.
В поле действительных чисел не всегда осуществима операция извлечения корня: не существует корень четной степени из отрицательного числа. Отсюда возникает задача дальнейшего расширения поля действительных чисел с целью получения такого множества чисел, в котором уравнение 
имело бы решение. Такое минимальное требование задачи расширения поля действительных чисел оправдывается тем, что при ее осуществлении становятся разрешимыми любые уравнения вида
.
Полем комплексных чисел называется минимальное поле С, содержащее поле R действительных чисел, т.е. множество С, обладающее свойствами:
1) С содержит поле действительных чисел, т.е. в С содержится такое подмножество R’, что 
;
2) C – поле;
3) в С разрешимо уравнение (целевое требование);
4) С – минимальное поле, т.е. не содержит никакого подполя, отличного от него самого и обладающего свойствами 1 – 3.
Элементы поля С – комплексные числа.
Под системой комплексных чисел понимают минимальное поле, которое является расширением поля действительных чисел и в котором есть элемент i с условием i + 1 = 0. В качестве первичных принимают следующие термины:
а) С — множество, его элементы называются комплексными числами;
б) +, • —сложение и умножение — бинарные операции на С;
в) 0, 1 и i — элементы С;
г) R — подмножество С, его элементы называются действительными числами;
д) Å и 8 — сложение и умножение — бинарные операции на R.
Для построения системы комплексных чисел воспользуемся исходным элементом – парой (a,b) действительных чисел. В процессе построения будут определены различные операции для таких пар.
Аксиомы разделяются на четыре группы и могут быть сформулированы так:
А
СI. 
;
СII. 
;
СIII. 
;
CIV. 
;
CV.
;
CVI.
;
CVII. 
;
СVIII.
;
CIX.
;
СХ. 
;
СХI.
.
Б
СХII.
- поле действительных чисел;
CХIII. R ÌC;
CХIV. 
;
CХV.
.
В
CXVI. 
.
Г
CXVII. (аксиома минимальности). Любое подмножество М множества С совпадает с С, если оно удовлетворяет следующим четырем условиям:
а) 
;
б) 
;
в) 
;
г) 
.
§2. Свойства комплексных чисел
Мы предполагаем, что 
— система комплексных чисел. Таким образом, для этой системы выполнены все названные в предыдущем разделе аксиомы.
Теорема 2.1. Всякое комплексное число 
можно представить и только одним способом в виде 
.
Доказательство. Предположим сначала, что 
для некоторых действительных чисел a, b, a1, b1. Поскольку 
— поле, то 
. Если 
, то 
.
А это не может быть в силу теоремы о том, что в линейно упорядоченном кольце квадрат любого не равного нулю элемента положителен. Возможность представления легко следует из аксиомы минимальности.
Определение 2.1. Суммой комплексных чисел (a,bi) и (c,di) называется комплексное число 
.
Сумму обозначают знаком «плюс». Поэтому определение можно записать так: 
.
Так как сложение комплексных чисел сводится к сложению действительных чисел, то сложение комплексных чисел всегда выполнимо и однозначно.
Теорема 2.2. Сложение комплексных чисел коммутативно и ассоциативно.
Доказательство. Проведем для ассоциативного закона. Вычислим 
. С другой стороны, 
. Следовательно, 
.
Комплексное число 
является нулем, ибо для любого комплексного числа 
справедливо 
.
Обычным образом, как, например, для рациональных чисел, доказывается единственность нуля.
Для всякого комплексного числа (a,b) существует противоположное ему комплексное число, обозначаемое 
. Проверим, что 
. В самом деле, 
. Единственность противоположного число доказывается обычным образом.
Теорема 2.3. Вычитание комплексных чисел всегда выполнимо и однозначно.
Доказательство. Проверим, что 
. Для этого вычислим сумму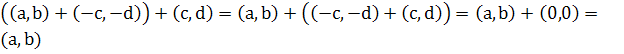 
.
Итак, 
. Последнее равенство удовлетворяет определению разности, следовательно, . Итак, вычитание выполнимо.
Докажем единственность разности. Пусть 
есть разность вида 
. Это значит, что 
. Прибавим к обеим частям 
. Получим 
. Этим доказана однозначность вычитания.
Определение 2.2. Произведением комплексных чисел и 
называется комплексное число 
.
Умножение обозначаем точкой, и определение тогда запишем так: 
.
Так как умножение комплексных чисел сводится к арифметическим действиям с действительными числами, то умножение всегда выполнимо и однозначно.
Теорема 2.4. Умножение комплексных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения, т.е.:
1) 
;
2) 
;
3) 
;
Доказательство. Проверим только дистрибутивный закон. Вычислим левую часть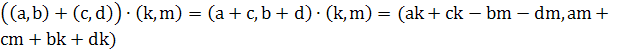 
. Вычислим правую часть 
.
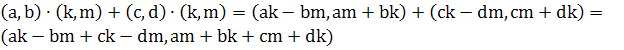Как видим левая и правая части оказались равными одному и тому же комплексному числу. Следовательно, они равны, т.е.: .
Комплексное число 
является единицей, ибо для любого комплексного числа справедливо 
.
Единственность единицы проверяется обычным образом. Пусть есть единица. Тогда 
, ибо – единица. Но – тоже единица, поэтому 
. Из однозначности умножения следует, что
.
Теорема 2.5. Для всякого комплексного числа 
существует обратное ему число, обозначаемое 
, т.е. такое, что их произведение равно единице.
Доказательство. Дано число , где 
или 
, т.е. 
. Найдем такое число 
, чтобы 
, откуда 
. Из определения равенства комплексных чисел следует 
Определитель системы 
, следовательно, система имеет решение, притом единственное: 
, 
. Таким образом, 
.
Следствие. Деление комплексных чисел всегда выполнимо (исключая деление на нуль) и однозначно.
Проверим, что 
есть 
. Вычислим: 
.
Итак, 
. Последнее равенство удовлетворяет определению частного, следовательно, 
. Итак, деление выполнимо.
Докажем единственность частного. Пусть 
. Это значит, что 
. Умножив обе части на 
, получим 
. Этим доказана однозначность деления.
На основании изложенного можно заключить, что множество комплексных чисел С является полем.
Выделим из поля С комплексных чисел множества CR пар вида 
. Комплексное число вида назовем действительным комплексным числом.
Теорема 3.1. Множество CR действительных комплексных чисел изоморфно полю R действительных чисел.
Доказательство. Действительному комплексному числу поставим в соответствие является взаимно-однозначным. Покажем, что указанное соответствие есть изоморфизм относительно сложения и умножения. Пусть 
, тогда 
и 
, т.е. 
. Следовательно, множество CR изоморфно полю R. Поэтому можно отождествить соответствующие элементы этих множеств и считать, что поле комплексных чисел С содержит поле действительных чисел. Действительное комплексное число в дальнейшем будем обозначать действительным числом а.
Комплексное число, не равное действительному, называется мнимым числом, т.е. , где есть мнимое число. Мнимое число 
называют чисто мнимым числом. Число 
назовем мнимой единицей и обозначим буквой i.
Покажем, что мнимая единица является решением уравнения . Действительно, 
. Итак, 
или 
.
Теорема 3.2. Всякое комплексное число может быть представлено в виде суммы действительного и чистого мнимого чисел.
Доказательство. Представим 
. Таким образом, 
. Выражение 
называется алгебраической или линейной формой комплексного числа .
На основании определений 2.1, 2.2 и теорем 2.3, 2.5 действия над комплексными числами в алгебраической форме можно записать так:
1) 
;
2) 
;
3) 
;
4) 
.
Сделаем такое заключение. При оперировании с комплексными числами их следует рассматривать как двучлены относительно буквы i. Получаемый при умножении член i2 надо заменить на (-1).
Теорема 3.3. Поле комплексных чисел С является минимальным расширением поля действительных чисел R.
Доказательство. Пусть подполе 
и отлично от 
. Это значит, что есть число 
, причем 
.
Возьмем число 
. Так как К – подполе, то вычитание и деление чисел из К снова принадлежат К. Следовательно 
. По тем же соображениям заключаем, что 
при любых а и b, т.е. К=С. Это значит, что собственных подполей, содержащих R, в С нет.
Теорема 3.4. Поле комплексных чисел не упорядоченное поле, т.е. не существует такого отношения «>», при котором выполняются условия:
1) для всякого комплексного числа z либо z>0, либо z<0, либо z=0;
2) если 
и 
, то 
и 
;
3) если 
, то 
, и наоборот.
Доказательство. При любом отношении «>» должно выполняться 1>0 (если предположить противное: 1<0, то по п.3 -1>0 и, согласно п.2, (-1)(-1)>0 или 1>0, что противоречит предположению 1<0).
Предположим, что для комплексных чисел существует такое отношение «>», при котором поле С будет упорядоченным полем. Возьмем 
. Так как 
, то 
, либо 
.
Рассмотрим . Тогда, согласно п.2, 
или -1>0. Получили противоречие.
Пусть . Тогда, согласно п.3, 
, откуда, согласно п.3, 
или 
. Получили противоречие. Предположив, что в поле комплексных чисел существует такое отношение «>», при котором поле С становится упорядоченным, мы установили, что для 
и 
нельзя определить, в каком они находятся отношении. Следовательно, поле комплексных чисел невозможно расположить никаким отношением «>».
§4. Категоричность аксиоматической теории комплексных чисел
Теорема 4.1. Пусть 
и 
— системы комплексных чисел. Тогда существует изоморфное отображение f системы 
на 
.
Доказательство. Прежде всего условливаемся в целях краткости пользоваться одинаковыми знаками операций в С' и R', а также в С" и R". Далее, условливаемся элементы из С' снабжать одним штрихом: 
, а элементы из С" двумя: 
Поскольку любые поля действительных чисел изоморфны, существует взаимно-однозначное отображение φ множества R' на R" такое, что:
1) 
;
2) 
.
Определим однозначное отображение f множества Cʹ в С" следующим условием: 
.
Нетрудно убедиться в том, что f — взаимно-однозначное отображение Сʹ на С".
Пусть 
. Имеем
.
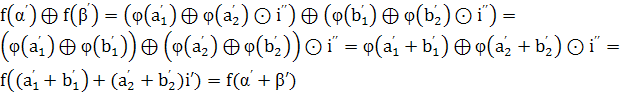Аналогично проверяется и условие 
.
§5. Непротиворечивость аксиоматической теории комплексных чисел
Теорема 5.1. Аксиоматическая теория комплексных чисел непротиворечива относительно аксиоматической теории действительных чисел.
Доказательство. Мы укажем модель данной теории. Пусть 
— поле действительных чисел. Рассмотрим множество Р пар 
действительных чисел и определим на Р бинарные операции Å и 8 (сложение и умножение) следующими условиями: 
.
Нам известно, что 
— поле. Выберем в Р подмножество R0 пар вида (а, 0). Сопоставим с каждым действительным числом а пару 
. Легко видеть, что φ — взаимно-однозначное отображение R на R0. Далее, имеем: 
.
Таким образом, φ — изоморфное отображение 
на 
Следовательно: а) 
— поле действительных чисел;
б) поле — расширение поля .
Заметим также, что (1, 0) и (0,0) — единица и нуль поля 
>. Полагаем 
. Имеем 
.
Итак, на системе 
выполняются первые 15 аксиом нашей теории. Пусть, наконец, М — подмножество Р такое, что:
а) 
;
б) ;
в) 
;
г) 
.
Докажем, что в таком случае любой элемент множества Р принадлежит множеству М. В самом деле, имеем 
.
Теорема доказана.
Построение моделей систем комплексных чисел способствовало лучшему пониманию их природы.
Пусть М – множество матриц второго порядка над полем действительных чисел вида 
. Множеству М принадлежит: нулевая матрица 0, единичная матрица Е и матрица I:
.
Проверим, что множество М замкнуто относительно сложения и умножения матриц, т.е. что сумма и произведение матриц принадлежат М:
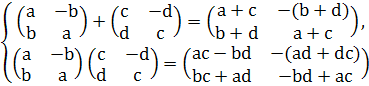(1)
Легко проверить, что умножение матриц коммутативно. Так как для матрицы 
определитель 
, то существует обратная матрица 
и, следовательно, в М осуществляется деление. Так что множество матриц из М образует поле.
Матрицу 
можно представить суммой
,
т.е. 
.
Из (1) следует правила сложения и умножения:
(2)
Установим взаимно-однозначное соответствие между комплексными числами 
и матрицами 
.
Из (2) вытекает, что соответствие сохраняется при выполнении арифметических операций. Следовательно, поле комплексных чисел изоморфно М; т.е. множество М является моделью поля комплексных чисел.
Представим матрицы в виде 
, где 
.
Так как 
, то существует такой угол 
, что 
. Отсюда 
.
Известно, что такие матрицы определяют последовательное выполнение поворота плоскости вокруг начала координат и растяжение плоскости с центром в начале координат с коэффициентом растяжения ρ. Таким образом, получено истолкование комплексного числа как хорошо известное преобразование плоскости.
Рассмотрим еще одну модель. Пусть М – множество многочленов 
одного переменного над полем действительных чисел. Множество М есть коммутативное кольцо. Будем говорить, что два многочлена 
и 
находятся в отношении (обозначим 
), если 
делится на многочлен 
. Очевидно, что тогда и только тогда, когда равны остатки от деления 
на . Отмечу, что остатки будут многочлены 
первой степени.
Теорема 6.1. Если 
и 
, то 
и 
.
Доказательство. Преобразуем 
. Каждая скобка делится на , следовательно, сумма делится на . Таким образом, . Аналогично доказывается для суммы.
Указанное отношение является отношением эквивалентности, ибо выполняются свойства:
1) рефлексивности: 
;
2) симметричности: если , то 
;
3) транзитивности: если и 
, то .
Отсюда следует, что кольцо многочленов распадается на непересекающиеся классы эквивалентных многочленов. Все многочлены одного класса имеют равные остатки от деления на , т.е. остаток (многочлена ) является характеристикой класса. Определим множество К, элементами и которого являются классы эквивалентных многочленов.
Сумма 
и произведение 
определяются следующим образом. Выбирают любые два многочлена 
, 
. Вычисляют 
и 
и находят классы, которым принадлежат сумма и произведение. Пусть 
. Тогда полагают 
. Согласно теореме 1, сумма и произведение не зависят от выбора представителей 
. Поэтому в качестве представителя будем всегда брать многочлен (единственный для данного класса) первой степени. Итак, множество К состоит только из многочленов первой степени.
Пусть 
. Произведение 
. Найдем класс, которому принадлежит произведение, т.е. остаток от деления его на . Очевидно, 
, и остаток равен 
.
Следовательно, произведение 
вычисляется по правилу 
.
Сумма 
.
Тем самым показано, что взаимно-однозначное соответствие между комплексными числами и элементами 
множества К устанавливает их изоморфизм. Итак, множество К есть поле комплексных чисел. Многочлен х играет роль мнимой единицы i и является решением уравнения .
Разберем несколько примеров моделей комплексных чисел.
№1.
Пусть М – множество всех матриц второго порядка над полем действительных чисел вида 
. Докажите, что множество М относительно операций сложения и умножения матриц изоморфно полю всех комплексных чисел С.
Решение:
комплексный действительный число матрица
– отображение.
- биектция
сохраняет операцию «+»
– сохраняет операцию «
». Значит операции «+» и «» биективно
№2.
В множестве R×R определены операции: а) 
; b) 
. Докажите, что алгебра
Решение:
a) ;
b)
Доказать: 
изоморфна полю 
, a,bϵR
Доказательство: 
.
????
№3
Пусть M=R(x) – кольцо многочленов от одной неизвестной над полем R. На М определим отношение 
дают одинаковые остатки при делении на многочлен . Докажите, что ρ – конгруэнция относительно сложения и умножения многочленов и фактор-кольцо
Решение:
М=R(x)
дают одинаковые остатки при делении на многочлен
Пусть 
в отношение 
.
.
, где 
,где
При сложение у нас получится одинаково 
разделив на
Получим 
№4.
Пусть Т=R×R×R – множество троек действительных чисел, на котором определены операции Å и 8 и бинарное отношение ρ:
,
,
.
Докажите: алгебра
1. 
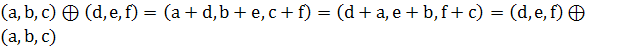коммутативность выполняется
2. 
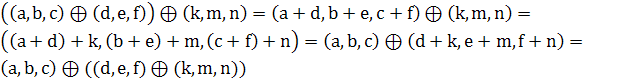ассоциативность выполняется
, 
- нейтральный элемент
, – симметричный элемент
Дистрибутивность 
1) 
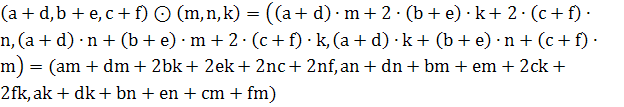
2) 
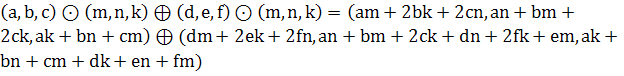. Дистрибутивность выполняется, т. к. (1)=(2) – доказано.
Заключение
Комплексные числа образуют алгебраически замкнутое поле – это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней. Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и естественных науках.
Что же такое модель комплексного числа?
Модель системы аксиом – это какой-либо математических объект, который отвечает данной системе аксиом. Истинность системы аксиом можно доказать, только построив модель в рамках другой системы аксиом, которая считается «истинной». Кроме того, модель позволяет наглядно продемонстрировать некоторые особенности данной аксиоматической теории.
И так модель комплексного числа это система аксиом применимых к данному комплексному числу, которую нужно доказать с помощью определенных операций.
Список используемой литературы
1. Блох Ш.А. Числовые системы. – Минск: Высшая школа, 1982.
2. Нечаев В. И. Числовые системы. – М.: Просвещение, 1975.
3. http://kvant.mirror1.mccme.ru/1982/03/kompleksnye_chisla.htm - Понтрягин Л., Комплексные числа. - журнал Квант №3, 1983. Электронная версия
4. http://ru.wikipedia.org/wiki/ - «Википедия» электронная энциклопедия
5. Феферман С., Числовые системы. – М.: Наука, 1971.
6. Ларин С. В., Числовые системы. – М.: Академия, 2001.
7. Reslib.com/book/Sbornik_zadach_po_algebre_i_teorii_chisel. – сборник задач по алгебре и теории чисел.