Скачать

Теоретическая физика: механика

План-конспект занятия

По теоретической физике

Студента V курса физико-математического факультета, гр. ОФ-61

Филатова Александра Сергеевича

Дата проведения занятия: 20.12.2000

Тема: «Канонические преобразования. Функция Гамильтона-Якоби. Разделение переменных»

Цели: Развить навык использования канонических преобразований. Закрепить умение осуществлять преобразования Лежандра для перехода к производящей функции от необходимых переменных. Научить использовать метод Гамильтона-Якоби при решении задач с разделением переменных. Сформировать понимание сути и могущественности метода. Воспитывать трудолюбие, прилежность.

Тип занятия: практическое.

Ход занятия

Краткие теоретические сведения

Канонические преобразования

Канонические преобразования переменных – это такие преобразования, при которых сохраняется канонический вид уравнений Гамильтона. Преобразования производят с помощью производящей функции, которая является функцией координат, импульсов и времени. Полный дифференциал производящей функции определяется следующим образом:

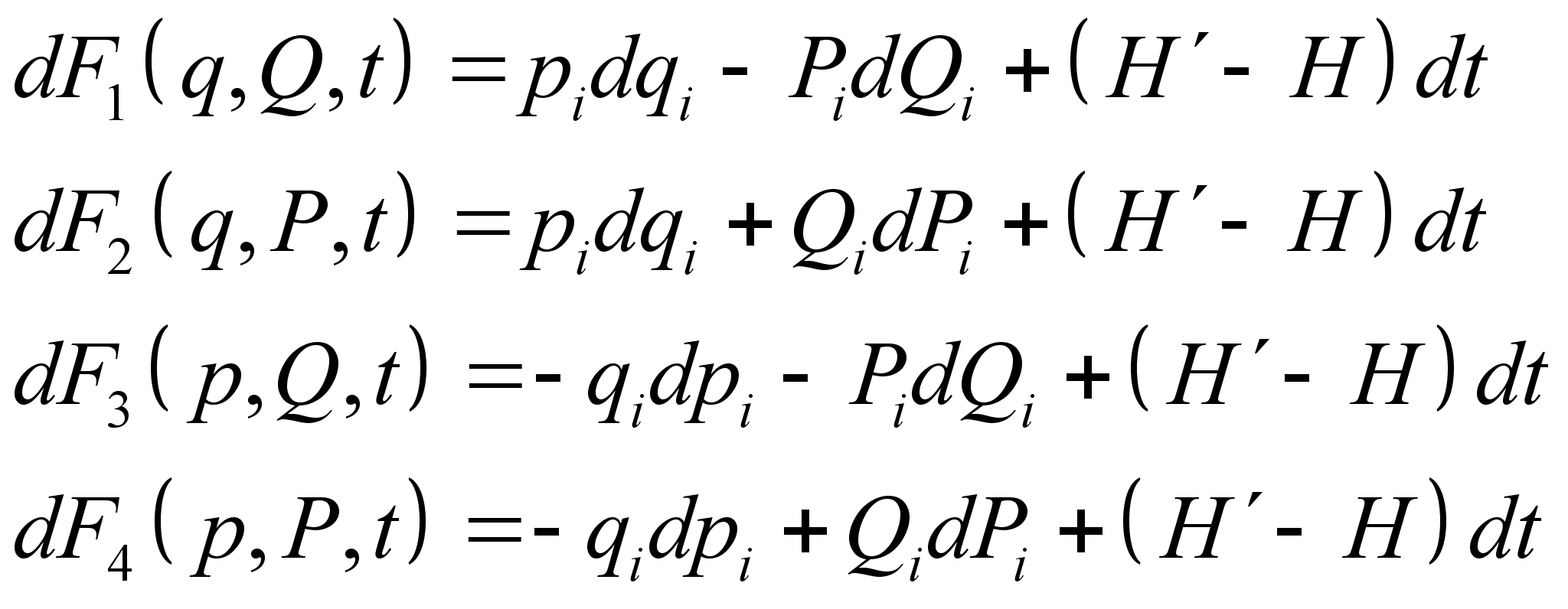
Выбирая производящую функцию от тех или иных переменных, получаем соответствующий вид канонических преобразований. Заметим, что если частная производная будет браться по "малым" , то будем получать малое , если же по "большим" , то и получать будем соответственно .

Функция Гамильтона-Якоби

При рассмотрении действия, как функции координат (и времени), следует выражение для импульса:

Из представления полной производной действия по времени следует уравнение Гамильтона-Якоби:

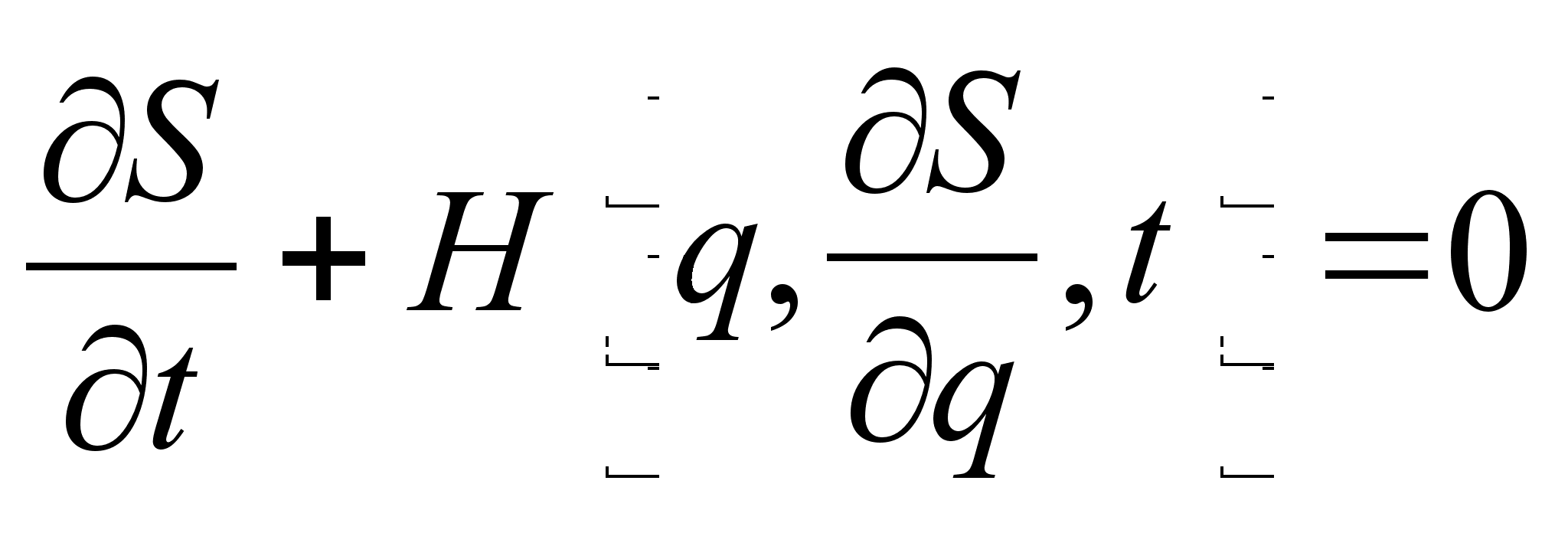
Здесь действие рассматривается как функция координат и времени: .

Путем интегрирования уравнения Гамильтона-Якоби , находят представление действия в виде полного интеграла, который является функцией координат, времени, и +1 постоянных ( – число степеней свободы). Поскольку действие входит в уравнение Гамильтона-Якоби только в виде производной, то одна из констант содержится в полном интеграле аддитивным образом, т.е. полный интеграл имеет вид:

Константа А не играет существенной роли, поскольку действие входит везде лишь в виде производной. А определяет, что, фактически, лишь констант меняют действие существенным образом. Эти константы определяются начальными условиями на уравнения движения, которые для любого значения А будут иметь одинаковый вид, как и само уравнение Гамильтона-Якоби.

Для того чтобы выяснить связь между полным интегралом уравнения Г.-Я. и интересующими нас уравнениями движения, необходимо произвести каноническое преобразование, выбрав полный интеграл действия в качестве производящей функции.

Константы будут выступать в качестве новых импульсов. Тогда новые координаты

тоже будут константы, поскольку

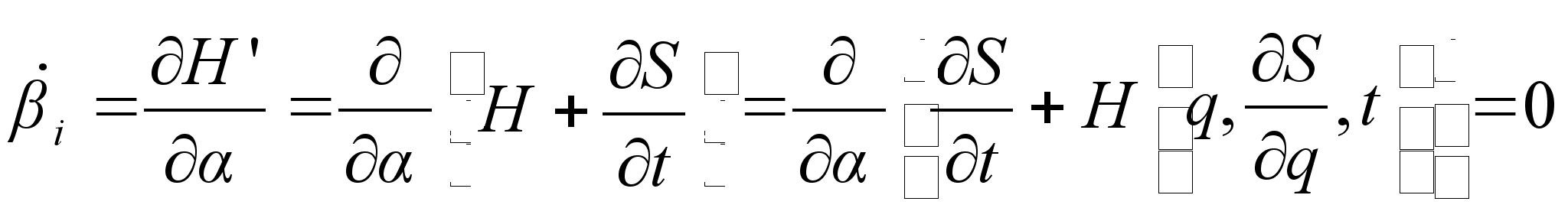
Выражая из уравнения координаты в виде функций от , мы и получим закон движения:

Решение задачи на нахождение зависимости существенно упрощается в случае разделения переменных. Такое возможно, когда какая-то координата может быть связана лишь с соответствующим ей импульсом и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.

Итак, нахождение уравнений движения методом Гамильтона-Якоби сводится к следующему:

1. составить функцию Гамильтона;

2. записать уравнение Г.-Я., и определить какие переменные разделяются;

3. Путем интегрирования уравнения Г.-Я. получить вид полного интеграла ;

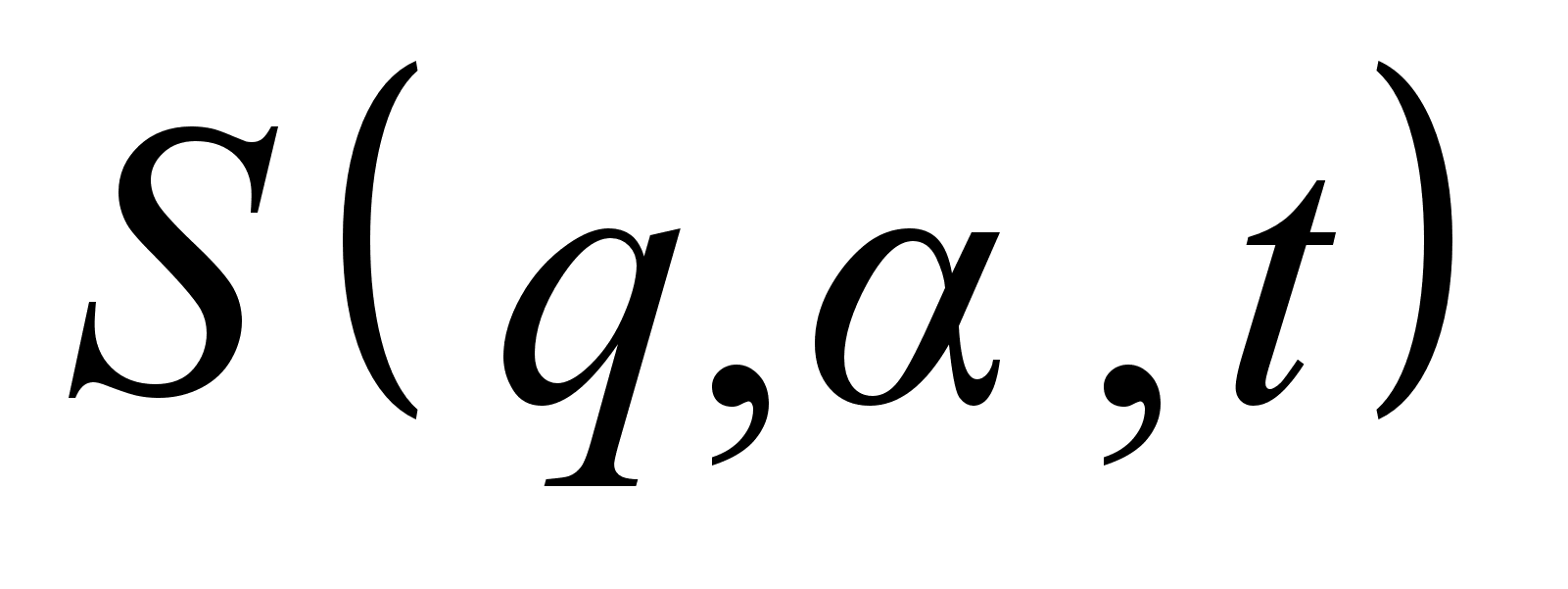4. Составить систему уравнений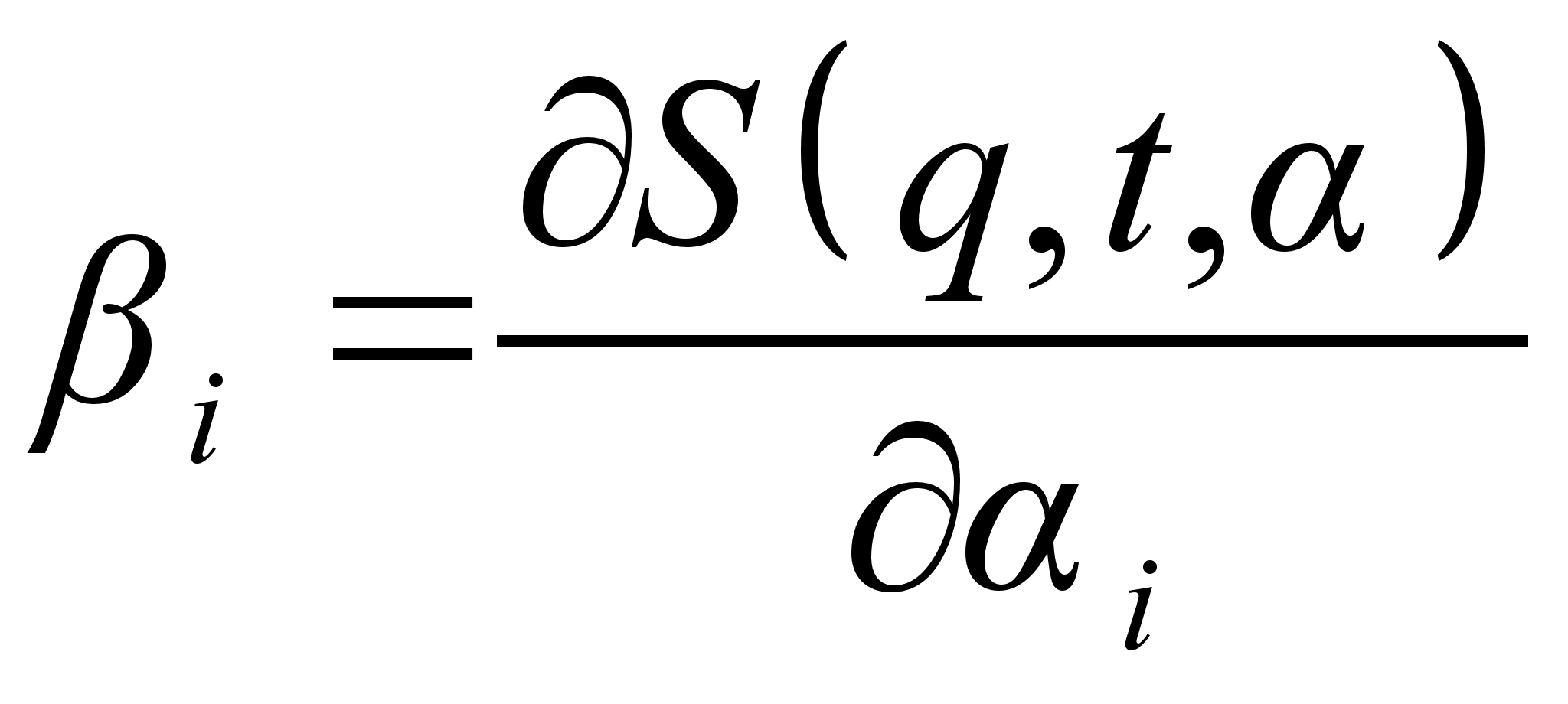, и получить закон движения ;

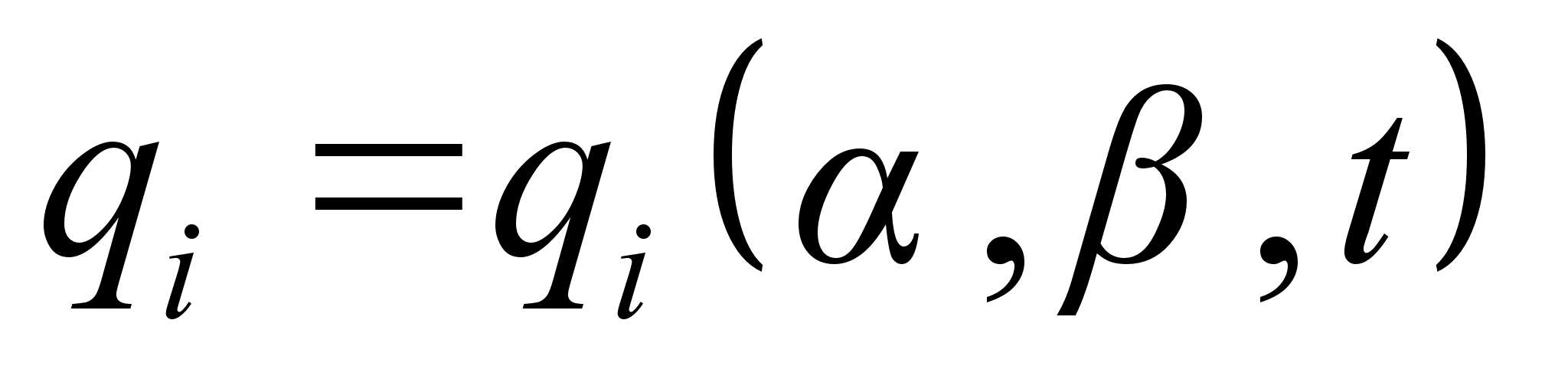5. По необходимости найти закон изменения импульсов: 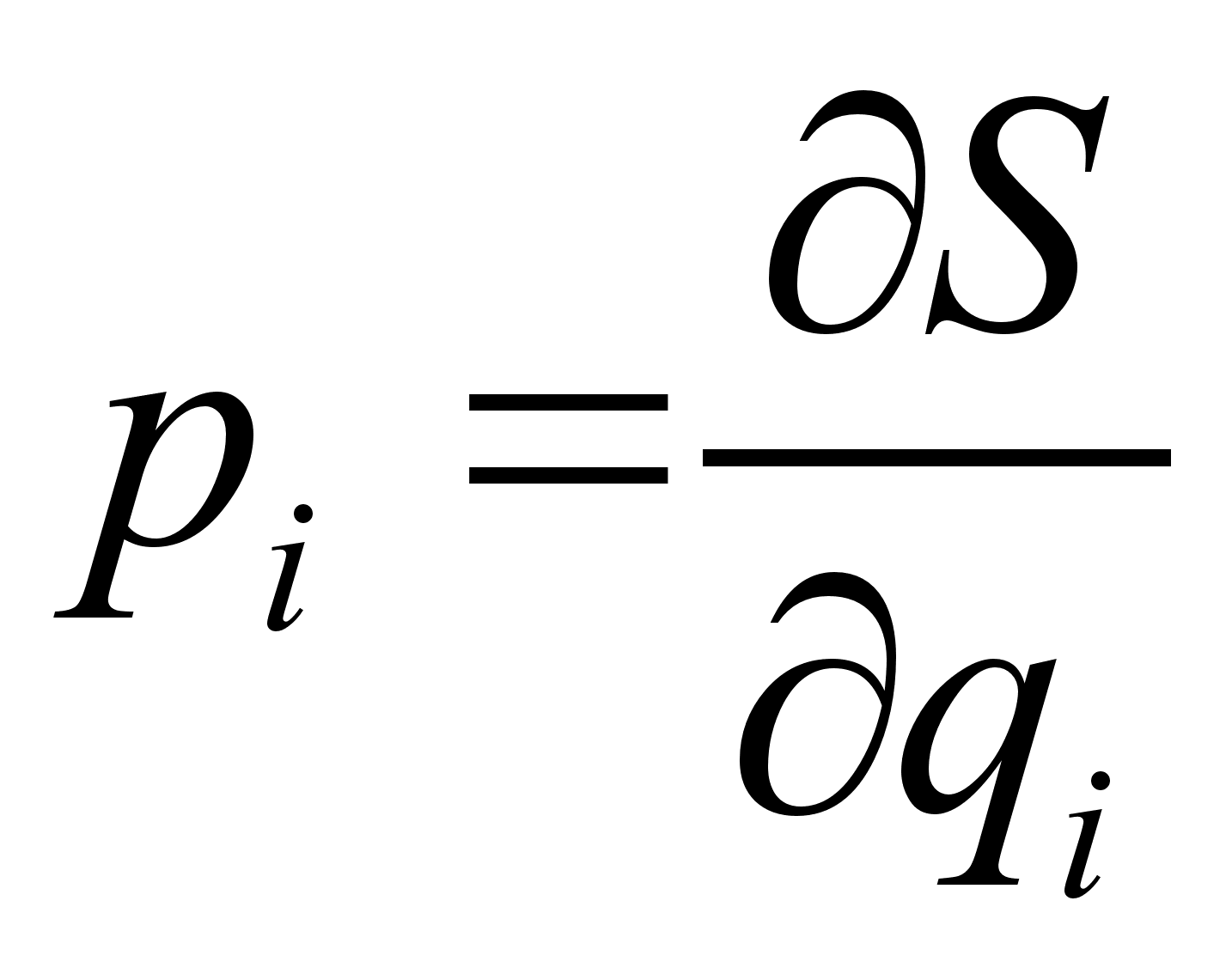. Для чего продифференцировать полный интеграл по координатам 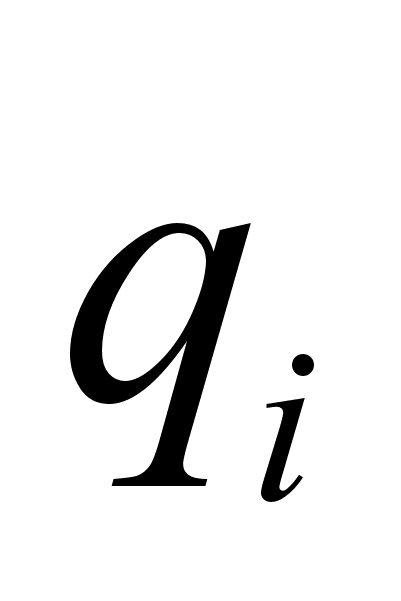, а потом подставить их явный вид, полученный в пункте 4.

Примеры решения задач

№11.14 () Как известно, замена функции Лагранжа на

,

где – произвольная функция, не изменяет уравнений Лагранжа. Показать, что это преобразование является каноническим, и найти его производящую функцию.

Решение:

Перепишем штрихованную функцию Лагранжа, представив полную производную функции через частные:

Функции Гамильтона, соответствующие штрихованной и не штрихованной функциям Лагранжа, определяются следующим образом:

Распишем , используя представление штрихованной функции Лагранжа :

Подставляя формулы и в выражение для штрихованной функции Гамильтона , получим:

Взаимно сократив второе слагаемое с последним, учитывая зависимость , получим:

Или

Но согласно каноническим преобразованием с производящей функцией Ф:

Следовательно,

Полученное соотношение определяет условие на временную часть производящей функции канонического преобразования, соответствующего преобразованию функции Лагранжа .

Поскольку вид обобщенных импульсов и координат при преобразовании функции Лагранжа не изменился, координатно-импульсная часть производящей функции должна соответствовать тождественному каноническому преобразованию. Как было показано в задаче №9.32 () (д/з пред. занятия), производящая функция определяющая тождественное каноническое преобразование с неизменным гамильтонианом, имеет вид:

Учитывая условие на временную часть производящей функции, окончательно получим:

Полученная производящая функция определяет тождественное каноническое преобразование с заменой функции Гамильтона соответствующей замене функции Лагранжа .

З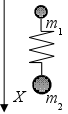адача. Система, состоящая из двух шариков массами , соединенных невесомой пружиной, расположенной вертикально, начинает двигаться в поле сил тяжести. Длина пружины - . Произвести каноническое преобразование и записать новую функцию Гамильтона, соответствующие производящей функции

.

Решение:

Составим функцию Гамильтона системы:

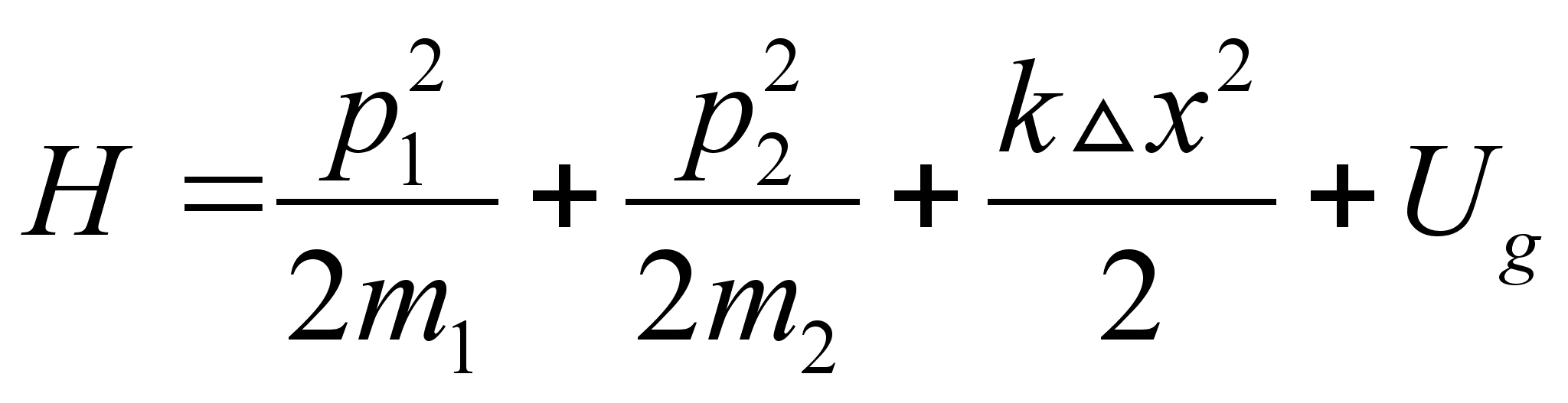
Здесь потенциальная энергия состоит из энергии гармонических колебаний и потенциальной энергии шариков в поле сил земного тяготения. По определению потенциального поля:

Мы имеем дело с одномерным движением, поэтому градиент в формуле заменяется производной по х. В то же время сила, является суммарной силой тяжести. Принимая во внимание принцип суперпозиции гравитационного поля, проинтегрируем последнее уравнение:

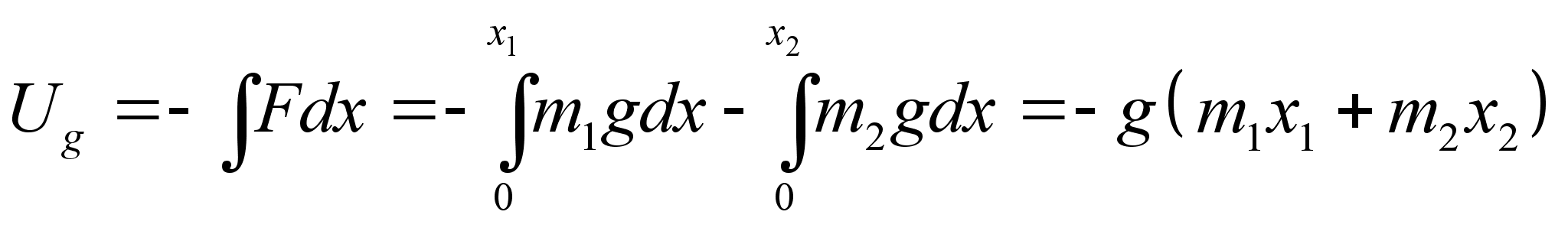
Значение смещения пружины от положения равновесия будет определяться следующим образом:

Подставив выражения и в формулу , получим вид функции Гамильтона, выраженной через импульсы и координаты явно:

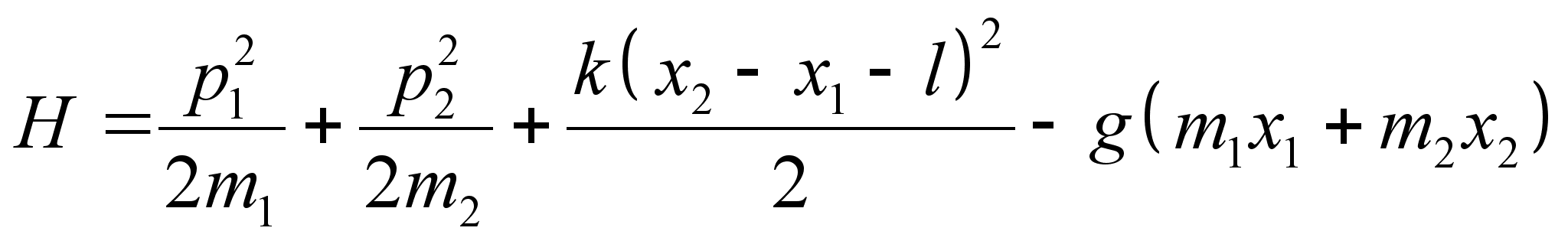
Переход к новым каноническим переменным производится в случае, когда возможно упростить вид функции Гамильтона, а соответственно и исходящих из нее уравнений движения.

В данной ситуации удобно выбрать новые координаты так, чтобы одна описывала движение центра масс системы, а вторая колебания пружины в собственной системе отсчета. Убедимся, что заданная в условии производящая функция отвечает именно такому преобразованию.

Новая координата совпадает со значением смещения пружины от положения равновесия.

Новая координата совпадает со значением положения центра масс системы.

Сложив оба уравнения, получим:

Соответственно

,

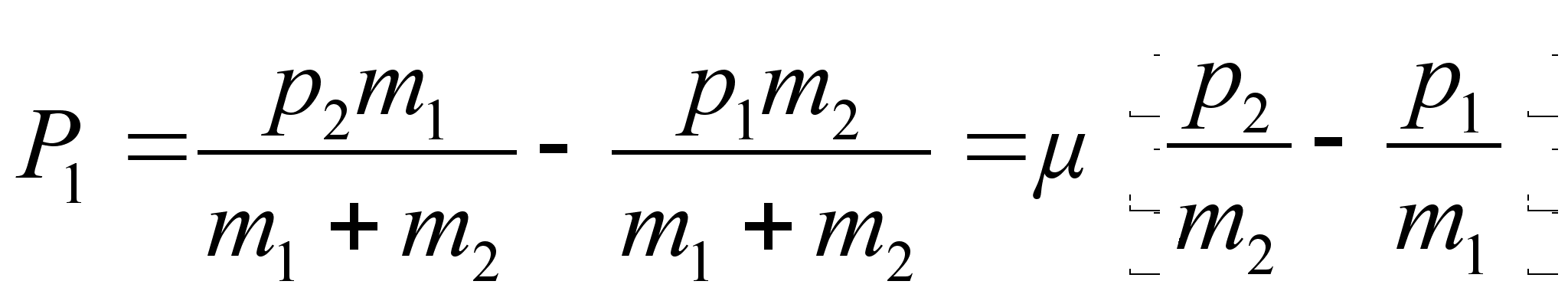где

,

– приведенная масса.

Запишем функцию Гамильтона в новых переменных:

,

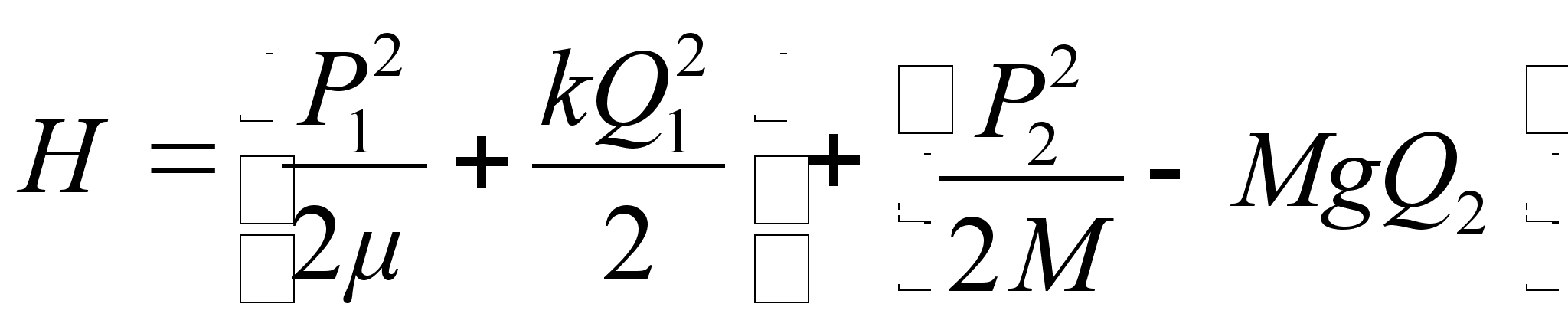где

,

– суммарная масса системы.

Действительно, функция Гамильтона в новых переменных распалась на две части, что соответствует двум парам канонических уравнений. Одна часть описывает колебания шариков в собственной системе отсчета, другая – движение системы как целого в поле сил тяжести.

№9.21 () Найти полный интеграл уравнения Г.-Я. и закон свободного движения материальной точки.

Решение:

1. Составим функцию Гамильтона свободной частицы:

2. Запишем уравнение Г.-Я.:

3. Произведем разделение переменных и проинтегрируем по времени.

Используем начальное условие:

Тогда подставляя вид функции S в уравнение Г.-Я. , последнее примет вид:

Откуда

Следовательно, полный интеграл уравнения Г.-Я.:

4. Закон движения определяется из канонического преобразования:

Откуда сам закон движения:

5. Импульс свободно движущейся материальной точки определяется следующим образом:

Действительно, частица в отсутствии внешнего поля движется с постоянным импульсом.

Домашнее задание:

№11.2 () Найти производящую функцию вида , приводящую к тому же каноническому преобразованию, что и .

Решение:

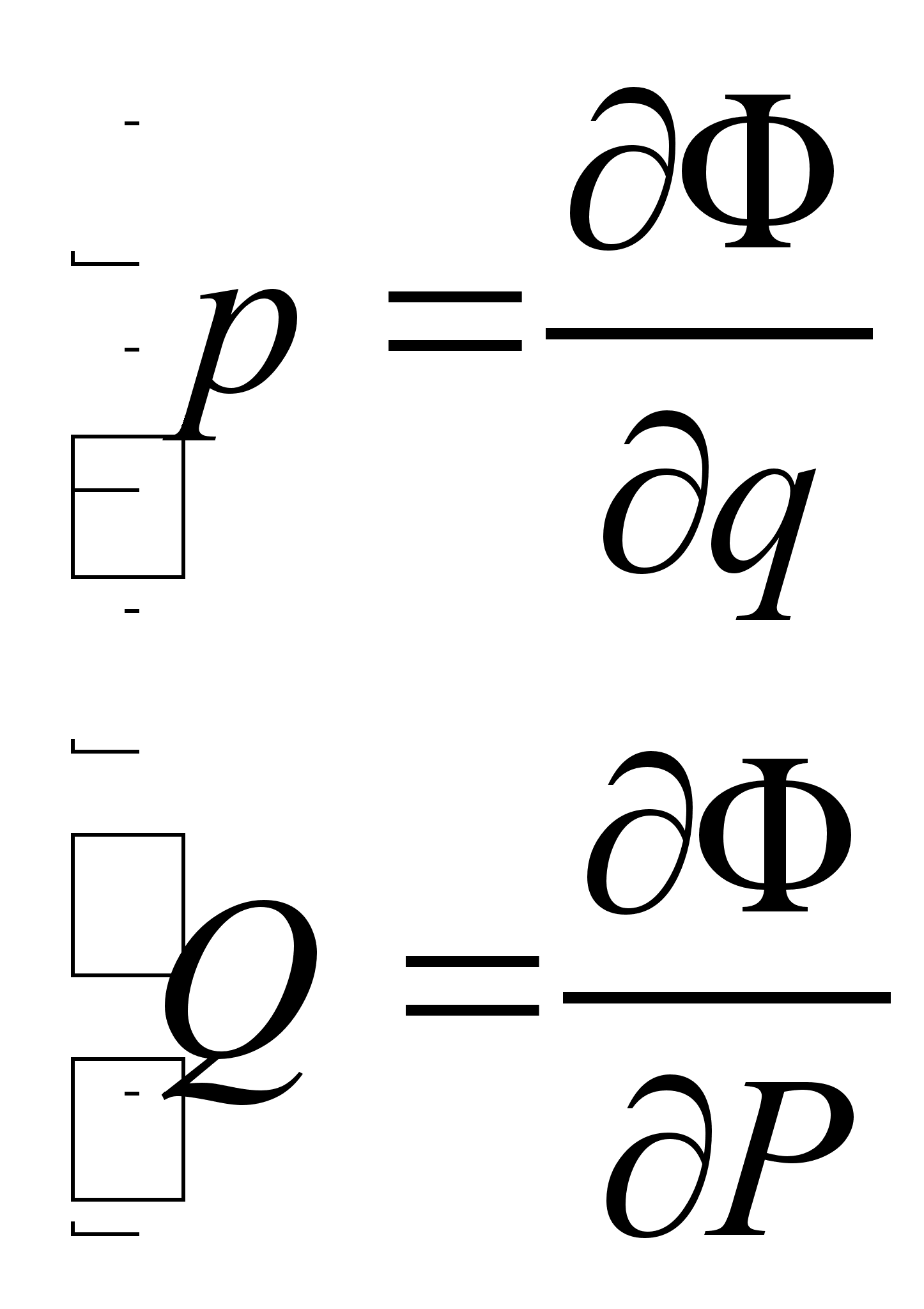
№9.38 () Найти уравнение, которому удовлетворяет производящая функция , порождающая каноническое преобразование к постоянным импульсам и координатам.

№9.23 () Найти полный интеграл уравнения Г.-Я. для тела, движущегося по гладкой наклонной плоскости, составляющей угол  с горизонтом.

№12.1 a) () Найти траекторию и закон движения частицы в поле

Литература:

1. Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», - М.: «Наука», 1969 г., - 272 с.

2. Л.Д. Ландау, Е.М. Лифшиц «Механика», - М.: «Наука», 1965 г., - 204 с.

3. И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», - М.: 1977 г., - 389 с.

4. Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с.

5. И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с.

6. Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с.

Студент-практикант: Филатов А.С.