Скачать

Статистический анализ числовых величин (непараметрическая статистика)

РЕФЕРАТ

Статистический анализ числовых величин (непараметрическая статистика)

В учебных курсах по теории вероятностей и математической статистике рассматривают различные параметрические семейства распределений числовых случайных величин. А именно, изучают семейства нормальных распределений, логарифмически нормальных, экспоненциальных, гамма-распределений, распределений Вейбулла-Гнеденко и др. Все они зависят от одного, двух или трех параметров. Поэтому для полного описания распределения достаточно знать или оценить одно, два или три числа. Очень удобно. Поэтому широко развита параметрическая теория математической статистики, в которой предполагается, что распределения результатов наблюдений принадлежат тем или иным параметрическим семействам.

К сожалению, параметрические семейства существуют лишь в головах авторов учебников по теории вероятностей и математической статистике. В реальной жизни их нет. Поэтому эконометрика использует в основном непараметрические методы, в которых распределения результатов наблюдений могут иметь произвольный вид.

Сначала на примере нормального распределения подробнее обсудим невозможность практического использования параметрических семейств для описания распределений конкретных экономических данных. Затем разберем параметрические методы отбраковки резко выделяющихся наблюдений и продемонстрируем невозможность практического использования ряда методов параметрической статистики, ошибочность выводов, к которым они приводят. Затем разберем непараметрические методы доверительного оценивания основных характеристик числовых случайных величин - математического ожидания, медианы, дисперсии, среднего квадратического отклонения, коэффициента вариации. Завершат главу методы проверки однородности двух выборок, независимых или связанных.

Распределение результатов наблюдений

В эконометрических и экономико-математических моделях, применяемых, в частности, при изучении и оптимизации процессов маркетинга и менеджмента, управления предприятием и регионом, точности и стабильности технологических процессов, в задачах надежности, обеспечения безопасности, в том числе экологической, функционирования технических устройств и объектов, разработки организационных схем часто применяют понятия и результаты теории вероятностей и математической статистики. При этом зачастую используют те или иные параметрические семейства распределений вероятностей. Наиболее популярно нормальное распределение. Используют также логарифмически нормальное распределение, экспоненциальное распределение, гамма-распределение, распределение Вейбулла-Гнеденко и т.д.

Очевидно, всегда необходимо проверять соответствие моделей реальности. Возникают два вопроса. Отличаются ли реальные распределения от используемых в модели? Насколько это отличие влияет на выводы?

Ниже на примере нормального распределения и основанных на нем методов отбраковки резко отличающихся наблюдений (выбросов) показано, что реальные распределения практически всегда отличаются от включенных в классические параметрические семейства, а имеющиеся отклонения от заданных семейств делают неверными выводы, в рассматриваемом случае, об отбраковке, основанные на использовании этих семейств.

Есть ли основания априори предполагать нормальность результатов измерений?

Иногда утверждают, что в случае, когда погрешность измерения (или иная случайная величина) определяется в результате совокупного действия многих малых факторов, то в силу Центральной Предельной Теоремы (ЦПТ) теории вероятностей эта величина хорошо приближается (по распределению) нормальной случайной величиной. Такое утверждение справедливо, если малые факторы действуют аддитивно и независимо друг от друга. Если же они действуют мультипликативно, то в силу той же ЦПТ аппроксимировать надо логарифмически нормальным распределением. В прикладных задачах обосновать аддитивность, а не мультипликативность действия малых факторов обычно не удается. Если же зависимость имеет общий характер, не приводится к аддитивному или мультипликативному виду, а также нет оснований принимать модели, дающие экспоненциальное, Вейбулла-Гнеденко, гамма или иные распределения, то о распределении итоговой случайной величины практически ничего не известно, кроме внутриматематических свойств типа регулярности.

При обработке конкретных данных иногда считают, что погрешности измерений имеют нормальное распределение. На предположении нормальности построены классические модели регрессионного, дисперсионного, факторного анализов, метрологические модели, которые еще продолжают встречаться как в отечественной ноpмативно-технической документации, так и в международных стандартах. На то же предположение опираются модели расчетов максимально достигаемых уровней тех или иных характеристик, применяемые при проектировании систем обеспечения безопасности функционирования экономических структур, технических устройств и объектов. Однако теоретических оснований для такого предположения нет. Необходимо экспериментально изучать распределения погрешностей.

Что же показывают результаты экспериментов? Сводка, данная в монографии (1), позволяет утверждать, что в большинстве случаев распределение погрешностей измерений отличается от нормального. Так, в Машинно-электротехническом институте (г. Варна в Болгарии) было исследовано распределение погрешностей градуировки шкал аналоговых электроизмерительных приборов. Изучались приборы, изготовленные в Чехословакии, СССР и Болгарии. Закон распределения погрешностей оказался одним и тем же. Он имеет плотность

Были проанализированы данные о параметрах 219 фактических распределениях погрешностей, исследованных разными авторами, при измерении как электрических, так и не электрических величин самыми разнообразными (электрическими) приборами. В результате этого исследования оказалось, что 111 распределений, т.е. примерно 50% , принадлежат классу распределений с плотностью

где  - параметр степени; b - параметр сдвига;  - параметр масштаба;  - гамма-функция от аргумента  ;

(см. (1, с. 56)); 63 распределения, т.е. 30%, имеют плотности с плоской вершиной и пологими длинными спадами и не могут быть описаны как нормальные или, например, экспоненциальные. Оставшиеся 45 распределений оказались двухмодальными.

В книге известного метролога проф. П. В. Hовицкого (2) приведены результаты исследования законов распределения различного рода погрешностей измерения. Он изучил распределения погрешностей электромеханических приборов на кернах, электронных приборов для измерения температур и усилий, цифровых приборов с ручным уpавновешиванием. Объем выборок экспериментальных данных для каждого экземпляра составлял 100-400 отсчетов. Оказалось, что 46 из 47 распределений значимо отличались от нормального. Исследована форма распределения погрешностей у 25 экземпляров цифровых вольтметров Щ-1411 в 10 точках диапазона. Результаты аналогичны. Дальнейшие сведения содержатся в монографии (1).

В лаборатории прикладной математики Тартуского государственного университета проанализировано 2500 выбоpок из архива реальных статистических данных. В 92% гипотезу нормальности пришлось отвергнуть.

Приведенные описания экспеpиментальных данных показывают, что погрешности измерений в большинстве случаев имеют распределения, отличные от нормальных. Это означает, в частности, что большинство применений критерия Стьюдента, классического регрессионного анализа и других статистических методов, основанных на нормальной теории, строго говоря, не является обоснованным, поскольку неверна лежащая в их основе аксиома нормальности распределений соответствующих случайных величин.

Очевидно, для оправдания или обоснованного изменения существующей практики анализа статистических данных требуется изучить свойства процедур анализа данных при "незаконном" применении. Изучение процедур отбраковки показало, что они крайне неустойчивы к отклонениям от нормальности, а потому применять их для обработки реальных данных нецелесообразно (см. ниже); поэтому нельзя утверждать, что произвольно взятая процедура устойчива к отклонениям от нормальности.

Иногда предлагают перед применением, например, критерия Стьюдента однородности двух выбоpок проверять нормальность. Хотя для этого имеется много критериев, но проверка нормальности - более сложная и трудоемкая статистическая процедура, чем проверка однородности (как с помощью статистик типа Стьюдента, так и с помощью непараметрических критериев). Для достаточно надежного установления нормальности требуется весьма большое число наблюдений. Так, чтобы гарантировать, что функция распределения результатов наблюдений отличается от некоторой нормальной не более, чем на 0,01 (при любом значении аргумента), требуется порядка 2500 наблюдений. В большинстве экономических, технических, медико-биологических и других прикладных исследований число наблюдений существенно меньше. Особенно это справедливо для данных, используемых при изучении проблем, связанных с обеспечением безопасности функционирования экономических структур и технических объектов.

Иногда пытаются использовать ЦПТ для приближения распределения погрешности к нормальному, включая в технологическую схему измерительного прибора специальные сумматоры. Оценим полезность этой меры. Пусть Z₁ , Z₂ ,…, Z_k - независимые одинаково распределенные случайные величины с функцией распределения H = H(x) такие, что  Рассмотрим

Показателем обеспечиваемой сумматором близости к нормальности является

Тогда

Правое неравенство в последнем соотношении вытекает из оценок константы в неравенстве Берри-Эссеена, полученном в книге (3, с.172), а левое - из примера в монографии (4, с.140-141). Для нормального закона  =1,6, для равномерного  = 1,3, для двухточечного  =1 (это - нижняя граница для ). Следовательно, для обеспечения расстояния (в метрике Колмогорова) до нормального распределения не более 0,01 для "неудачных" распределений необходимо не менее k₀ слагаемых, где

В обычно используемых сумматорах слагаемых значительно меньше. Сужая класс возможных распределений H, можно получить, как показано в монографии (5), более быструю сходимость, но теория здесь еще не смыкается с практикой. Кроме того, не ясно, обеспечивает ли близость распределения к нормальному (в определенной метрике) также и близость распределения статистики, построенной по случайным величинам с этим распределением, к распределению статистики, соответствующей нормальным результатам наблюдений. Видимо, для каждой конкретной статистики необходимы специальные теоретические исследования, Именно к такому выводу приходит автор монографии (5). В задачах отбраковки выбросов ответ: "Не обеспечивает" (см. ниже).

Отметим, что результат любого реального измерения записывается с помощью конечного числа десятичных знаков, обычно небольшого (2-5), так что любые реальные данные целесообразно моделировать лишь с помощью дискретных случайных величин, принимающих конечное число значений. Нормальное распределение - лишь аппроксимация реального распределения. Так, например, данные конкретного исследования, приведенные в работе (6), принимают значения от 1,0 до 2,2, т.е. всего 13 возможных значений. Из принципа Дирихле следует, что в какой-то точке построенная по данным работы (6) функция распределения отличается от ближайшей функции нормального распределения не менее чем на 1/26, т.е. на 0,04. Кроме того, очевидно, что для нормального распределения случайной величины вероятность попасть в дискретное множество десятичных чисел с заданным числом знаков после запятой равна 0.

Из сказанного выше следует, что результаты измерений и вообще статистические данные имеют свойства, приводящие к тому, что моделировать их следует случайными величинами с распределениями, более или менее отличными от нормальных. В большинстве случаев распределения существенно отличаются от нормальных, в других нормальные распределения могут, видимо, рассматриваться как некоторая аппроксимация, но никогда нет полного совпадения. Отсюда вытекает как необходимость изучения свойств классических статистических процедур в неклассических вероятностных моделях (подобно тому, как это сделано ниже для критерия Стьюдента), так и необходимость разработки устойчивых (учитывающих наличие отклонений от нормальности) и непараметрических, в том числе свободных от распределения процедур, их широкого внедрения в практику статистической обработки данных.

Опущенные здесь рассмотрения для других параметрических семейств приводят к аналогичным выводам. Итог можно сформулировать так. Распределения реальных данных практически никогда не входят в какое-либо конкретное параметрическое семейство. Реальные распределения всегда отличаются от тех, что включены в параметрические семейства. Отличия могут быть большие или маленькие, но они всегда есть. Попробуем понять, насколько важны эти различия для проведения эконометрического анализа.

Неустойчивость параметрических методов отбраковки резко выделяющихся результатов наблюдений

При обработки реальных экономических данных, полученных в процессе наблюдений, измерений, расчетов, иногда один или несколько результатов наблюдений резко выделяются, т.е. далеко отстоят от основной массы данных. Такие резко выделяющиеся результаты наблюдений часто считают содержащими грубые погрешности, соответственно называют промахами или выбросами. В рассматриваемых случаях возникает естественная мысль о том, что подобные наблюдения не относятся к изучаемой совокупности, поскольку содержат грубую погрешность, а получены в результате ошибки, промаха. В метрологии об этом явлении говорят так: "Грубые погрешности и промахи возникают из-за ошибок или неправильных действий оператора (его психо-физиологического состояния, неверного отсчета, ошибок в записях или вычислениях, неправильного включения приборов и т.п.), а также при кратковременных резких изменений проведения измерений (вибрации, поступления холодного воздуха, толчка прибора оператором и т.п.). Если грубые погрешности и промахи обнаруживают в процессе измерений, то результаты, содержащие их, отбрасывают. Однако чаще всего их выявляют только при окончательной обработке результатов измерений с помощью специальных критериев оценки грубых погрешностей" (7, с.46-47).

Есть два подхода к обработке данных, которые могут быть искажены грубыми погрешностями и промахами:

1) отбраковка резко выделяющихся результатов наблюдений, т.е. обнаружение наблюдений, искаженных грубыми погрешностями и промахами, и исключение их из дальнейшей статистической обработки;

2) применение устойчивых (робастных) методов обработки данных, На результаты работы которых мало влияет наличие небольшого числа грубо искаженных наблюдений (см. ниже соответствующую главу).

В настоящем пункте обсуждаются методы отбраковки.

Наиболее изучена ситуация, когда результаты наблюдений - числа x₁., x₂.,…, x_n., резко выделяется один результат наблюдения, для определенности, максимальный x_max .

Простейшая вероятностно-статистическая модель такова (8). При нулевой гипотезе H₀ результаты наблюдения x₁., x₂.,…, x_n рассматриваются как реализация независимых одинаково распределенных случайных величин числа X₁., X₂.,…, X_n. с функцией распределения F(x). При альтернативной гипотезе H₁ случайные величины X₁., X₂.,…, X_n. также независимы, X₁., X₂.,…, X_n-1 имеют распределение F(x), а X_n - распределение G(x), оно "существенно сдвинуто вправо" относительно F(x), например, G(x)=F(x - A), где A достаточно велико. Если альтернативная гипотеза справедлива, то при вероятность равенства

стремится к 1, поэтому естественно применять решающее правило следующего вида:

если x_max.> d, то принять H₁.,

если x_max.< d, то принять H₀ , (1)

где d - параметр решающего правила, который следует определять из вероятностно-статистических соображений.

При справедливости нулевой гипотезы

Статистический критерий проверки гипотезы H₀ , основанный на решающем правиле вида (1), имеет уровень значимости , если

т.е.

         (2)

Из соотношения (2) определяют граничное значение d=d(, n) в решающем правиле (1).

При больших n и малых

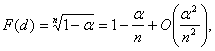     (3)

поэтому в качестве хорошего приближения к d(, n) рассматривают (1-/n) - квантиль распределения F(x).

Пусть правило отбраковки задано в соответствии с выражениями (1) и (2) с некоторой функцией распределения F, однако выборка берется из функции распределения G, мало отличающейся от F в смысле расстояния Колмогорова

     (4)

С помощью соотношения (3) получаем, что величина = G(d) для d из уравнения (2) находится между  и . Уровень значимости критерия, построенного для F, при применении к наблюдениям из G есть 1- и может принимать любые значения в отрезке (1-; 1-). В частности, при = 0,01, =0,05, n = 5 возможные значения уровня значимости заполняют отрезок (0; 0,1), т.е. уровень значимости может быть в 2 раза выше номинального, а если n возрастает до 30, то максимальный уровень значимости есть 0,297, т.е. почти в 6 раз выше номинального. При дальнейшем росте n верхняя граница для уровня значимости, как нетрудно видеть, приближается к 1.

Рассмотрим и другой вопрос - насколько правило отбраковки с уровнем значимости  для G может отличаться от такового для F при справедливости неравенства (4). С использованием соотношения (3) заключаем, что из

           (5)

следует, что  где  и  выписаны выше. Решение уравнения (5) может принимать любое значение в отрезке (). В частности, при =0,05 и n = 5 для стандартного нормального распределения F имеем d(, n) = 2,319, при =0,01 решение уравнения (5) может принимать любое значение в отрезке (2,054; + ), при  =0,005 - любое значение в (2,170; 2,576).

При использовании любого другого расстояния между функциями распределения выводы о неустойчивости правил отбраковки также справедливы. Отметим, что проведенные рассмотрения выполнены в рамках "общей схемы устойчивости" (см. ниже главу об устойчивости статистических процедур).

Рассмотренные примеры показывают, что при конкретном значении = 0,01 в неравенстве (4) весьма неустойчивы как уровни значимости при фиксированном правиле отбраковки, так и параметр d правила отбраковки при фиксированном уровне значимости. Обсудим, насколько реалистично определение функции распределения с точностью

Есть два подхода к определению функции распределения результатов наблюдений: эвристический подбор с последующей проверкой с помощью критериев согласия и вывод из некоторой вероятностной модели.

Пусть с помощью критерия согласия Колмогорова проверяется гипотеза о том, что выборка взята из распределения F. Пусть функции распределения F и G удовлетворяют соотношению (4). Пусть на самом деле выборка взята из распределения G, а не F. При каких  не удастся различить F и G? Для определенности, при каких гипотеза согласия с F будет приниматься не менее чем в 50% случаев?

Критерий согласия Колмогорова основан на статистике

     (6)

где расстояние между функциями распределения определено выше в формуле (4); H - та функция распределения, согласие с которой проверяется, а F_n- эмпирическая функция распределения (т.е. F_n(х) равно доле наблюдений, меньших х, в выборке объема n). Как показал А.Н. Колмогоров в 1933 г., функция распределения случайной величины  при росте объема выборки n сходится к некоторой функции распределения К(х), которую ныне называют функцией Колмогорова. При этом К(1,36)= 0,95 и К(0,83)=0,50.

Поскольку выборка взята из распределения G, то с вероятностью 0,50

           (7)

(при больших n). Тогда для рассматриваемой выборки с учетом неравенства (4) и неравенства треугольника для расстояния Колмогорова и симметричности этого расстояния имеем

Если

т.е.

            (8)

то, согласно формуле (6), гипотеза согласия принимается по крайней мере с той же вероятностью, с которой выполнено неравенств (7), т.е. с вероятностью не менее 0,50. Для = 0,01 это условие выполняется при n < 2809. Таким образом, для определения функции распределения с точностью с помощью критерия согласия Колмогорова необходимо несколько тысяч наблюдений, что для большинства эконометрических задач нереально.

При втором из названных выше подходов к определению функции распределения ее конкретный вид выводится из некоторой системы аксиом, в частности, из некоторой модели порождения соответствующей случайной величины. Например, из модели суммирования вытекает нормальное распределение, а из мультипликативной модели перемножения - логарифмически нормальное распределение. Как правило, при выводе используется предельный переход. Так, из Центральной Предельной Теоремы теории вероятностей вытекает, что сумма независимых случайных величин может быть приближена нормальным распределением. Однако более детальный анализ, в частности, с помощью неравенства Берри-Эссеена (см. предыдущий пункт) показывает, что для гарантированного достижения точности необходимо более полутора тысяч слагаемых. Такого количества слагаемых реально, конечно, указать почти никогда нельзя. Это означает, что при решении практических эконометрических задач теория дает возможность лишь сформулировать гипотезу о виде функции распределения, а проверять ее надо с помощью анализа реальной выборки объема, как показано выше, не менее нескольких тысяч.

Таким образом, в большинстве реальных ситуаций определить функцию распределения с точностью  невозможно.

Итак, показано, что правила отбраковки, основанные на использовании конкретной функции распределения, являются крайне неустойчивыми к отклонениям от нее распределения элементов выборки, а гарантировать отсутствие подобных отклонений невозможно. Поэтому отбраковка по классическим правилам математической статистики не является научно обоснованной, особенно при больших объемах выборок. Указанные правила целесообразно применять лишь для выявления "подозрительных" наблюдений, вопрос об отброаковке которых должен решаться из соображений соответствующей предметной области, а не из формально-математических соображений.

Выше для простоты изложения рассмотрен лишь случай полностью известного распределения F, для которого изучено правило отбраковки, заданное формулами (1) и (2). Аналогичные выводы о крайней неустойчивости правил отбраковки справедливы, если "истинное распределение" принадлежит какому-либо параметрическому семейству, например, нормальному, Вейбулла-Гнеденко, гамма.

Параметрическим методам отбраковки, основанным на моделях тех или иных параметрических семейств распределений, посвящены тысячи книг и статей. Приходится признать, что они имеют в основном внутриматематический интерес. При обработке реальных данных следует применять устойчивые методы (см. соответствующую главу), в частности, непараметрические.

Пусть исходные данные –это выборка x₁, x₂, … , x_n , где n – объем выборки. Выборочные значения x₁, x₂, … , x_n рассматриваются как реализации независимых одинаково распределенных случайных величин X₁, X₂, … , X_n с общей функцией распределения F(x) = P (X_i < x), i = 1,2, …, n. Поскольку функция распределения произвольна (с точностью до условий регулярности типа существования моментов), то рассматриваемые задачи доверительного оценивания характеристик распределения являются непараметрическими. Существование моментов является скорее математическим ограничением, чем реальным, поскольку практически все реальные статистические данные финитны (ограничены сверху и снизу, например, шкалой прибора).

В расчетах будут использоваться выборочное среднее арифметическое

M = (X₁ + X₂ +… + X _n ) / n,

выборочная дисперсия

S² = { (X₁ – M)² + (X₂ – M)²+… + (X _n – M)² } / (n-1)

и некоторые другие выборочные характеристики, которые мы введем позже.

Точечное и интервальное оценивание математического ожидания. Точечной оценкой для математического ожидания в силу закона больших чисел является выборочное среднее арифметическое М.

M – U(p) S / n^1/2 ,

где:

M – выборочное среднее арифметическое,

p – доверительная вероятность (истинное значение математического ожидания находится между нижней доверительной границей и верхней доверительной границей с вероятностью, равной доверительной);

U(p) – число, заданное равенством Ф(U(p)) = (1+ p)/2, где Ф(х) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Например, при p = 95% (т.е. при р = 0,95) имеем U(p) = 1,96. Функция U(p) имеется в большинстве литературных источников по теории вероятностей и математической статистике (см., например, (8));

S – выборочное среднее квадратическое отклонение (квадратный корень из описанной выше выборочной дисперсии).

M + U(p) S / n^1/2 .

С(р) = (n/2 – U(p)n^1/2 /2) ,

где (.) – знак целой части числа. Нижняя доверительная граница для медианы имеет вид

Х (С(р)),

где Х(i) – член вариационного ряда с номером i, построенного по исходной выборке (т.е. i-я порядковая статистика). Верхняя доверительная граница для медианы имеет вид

Х (n + 1 - С(р)).

d² = (m ₄ - ((n – 1) /n ) ⁴ S ⁴ ) / n ,

где m ₄ - выборочный четвертый центральный момент, т.е.

m ₄ = { (X₁ – M) ⁴ + (X₂ – M) ⁴+… + (X _n – M) ⁴ } / n .

Íèæíÿÿ äîâåðèòåëüíàÿ ãðàíèöà äëÿ äèñïåðñèè ñëó÷àéíîé âåëè÷èíû èìååò âèä

S² - U(p)d,

где S² – выборочная дисперсия,

U(p) – квантиль нормального распределения порядка (1+р)/2 (как и раньше),

d –положительныйквадратный корень из величины d², введенной выше.

S² + U(p)d,

где все составляющие имеют тот же смысл, что и выше.

При выводе приведенных соотношений используется асимптотическая нормальность выборочной дисперсии, установленная, например, в (10, с.419). Соответственно доверительный интервал является непараметрическим и асимптотическим. В классическом случае точечная оценка имеет тот же вид, а вот доверительные границы находят с помощью квантилей распределения хи-квадрат с числом степеней свободы, на 1 меньшим объема выборки. Отметим, что в случае нормального распределения четвертый момент в 3 раза больше квадрата дисперсии, а потому можно оценить d² как (2 S ⁴ ) / n . Это дает быстрый способ для интервальной оценки дисперсии в нормальном случае.

Точечное и интервальное оценивание среднего квадратического отклонения. Дисперсия рассматриваемой случайной величины - выборочного среднего квадратического отклонения S – оценивается как дробь

d² / (4 S² ) .

S - U(p)d / (2S),

где S² – выборочная дисперсия,

U(p) – квантиль нормального распределения порядка (1+р)/2 (как и раньше),

d –положительныйквадратный корень из величины d², введенной выше.

S + U(p)d / (2S),

где все составляющие имеют тот же смысл, что и выше.

Правила расчетов настоящего подпункта получены из правил предыдущего подпункта с помощью метода линеаризации (см., например, (11, п.2.4)). В рассматриваемом случае доверительный интервал также является непараметрическим и асимптотическим, а классический подход связан с использованием распределения хи-квадрат.

Точечное и интервальное оценивание коэффициента вариации. Коэффициент вариации широко используется при анализе конкретных экономических данных (поскольку они, как правило, положительны), но не очень популярен среди теоретиков. Дисперсия выборочного коэффициента вариации

V_n = S / M

D² = (V_n⁴ - V_n² / 4 + m ₄ / (4 S ² M ²) - m ₃ /M ³ ) / n ,

где М – выборочное среднее арифметическое,

S ²– выборочная дисперсия,

m ₃- выборочный третий центральный момент, т.е.

m ₃ = { (X₁ – M) ³ + (X₂ – M) ³+… + (X _n – M) ³ } / n ,

m ₄- выборочный четвертый центральный момент (см. выше),

V_n– выборочный коэффициент вариации,

n - объем выборки.

V_n - U(p) D,

где V_n– выборочный коэффициент вариации,

U(p) – квантиль нормального распределения порядка (1+р)/2 (как и ранее),

D –положительныйквадратный корень из величины D², введенной выше.

V_n + U(p) D,

где все составляющие имеют тот же смысл, что и выше.

Как и в предыдущих случаях, доверительный интервал является непараметрическим и асимптотическим. Он получен в результате применения специальной технологии вывода асимптотических соотношений прикладной статистики. Эта технология в качестве первого шага использует многомерную центральную предельную теорему, примененную к сумме векторов, координаты которых – степени исходных случайных величин. Второй шаг – преобразование предельного многомерного нормального вектора с целью получения интересующего исследователя вектора. При этом используются соображения линеаризации и отбрасываются бесконечно малые величины. Третий шаг – строгое обоснование полученных результатов на стандартном для асимптотических математико-статистических рассуждений уровне. При этом обычно оказывается необходимым использовать необходимые и достаточные условия наследования сходимости, полученные в монографии (11, п.2.4). Именно таким образом были получены приведенные выше результаты для выборочного коэффициента вариации. Формулы оказались существенно более сложными, чем в предыдущих случаях. Это объясняется тем, что выборочный коэффициент вариации - функция двух выборочных моментов, а ранее рассматривались либо выборочные моменты поодиночке, либо функция от одного выборочного момента - выборочной дисперсии.

О проверке однородности двух независимых выборок

Противоположным понятием является «различие». Можно переформулировать задачу: требуется проверить, есть ли различие между выборками. Если различия нет, то для дальнейшего изучения часто выборки объединяют.

Например, в маркетинге важно выделить сегменты потребительского рынка. Если установлена однородность двух выборок, то возможно объединение сегментов, из которых они взяты, в один. В дальнейшем это позволит осуществлять по отношению к ним одинаковую маркетинговую политику (проводить одни и те же рекламные мероприятия и т.п.). Если же установлено различие, то поведение потребителей в двух сегментах различно, объединять эти сегменты нельзя, и могут понадобиться различные маркетинговые стратегии, своя для каждого из этих сегментов.

Традиционный метод проверки однородности (критерий Стьюдента). Для дальнейшего критического разбора опишем традиционный статистический метод проверки однородности. Вычисляют средние арифметические в каждой выборке

 ,

затем выборочные дисперсии

 ,

и статистику Стьюдента t, на основе которой принимают решение,

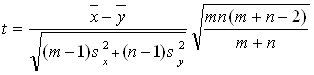 . (1)

По заданному уровню значимости a и числу степеней свободы (m+n ^_ 2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t|>t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t|кр, то принимают. (При односторонних альтернативных гипотезах вместо условия |t|>t_крпроверяют, что t>t_кр; эту постановку рассматривать не будем, так как в ней нет принципиальных отличий от обсуждаемой здесь.)

Рассмотрим условия применимости традиционного метода проверки однородности, основанного на использовании статистики t Стьюдента, а также укажем более современные методы.

Вероятностная модель порождения данных. Для обоснованного применения эконометрических методов необходимо прежде всего построить и обосновать вероятностную модель порождения данных. При проверке однородности двух выборок общепринята модель, в которой x₁, x₂,...,x_m рассматриваются как результаты m независимых наблюдений некоторой случайной величины Х с функцией распределения F(x), неизвестной статистику, а y₁, y₂,...,y_n - как результаты п независимых наблюдений, вообще говоря, другой случайной величины Y с функцией распределения G(x), также неизвестной статистику. Предполагается также, что наблюдения в одной выборке не зависят от наблюдений в другой, поэтому выборки и называют независимыми.

Возможность применения модели в конкретной реальной ситуации требует обоснования. Независимость и одинаковая распределенность результатов наблюдений, входящих в выборку, могут быть установлены или исходя из методики проведения конкретных наблюдений, или путем проверки статистических гипотез независимости и одинаковой распределенности с помощью соответствующих критериев (8).

Если проведено (т+п) измерений объемов продаж в (т+п) торговых точках, то описанную выше модель, как правило, можно применять. Если же, например, x_i и y_i - объемы продаж одного и того же товара до и после определенного рекламного воздействия, то рассматриваемую модель применять нельзя. (В этом случае используют модель т.н. связанных выборок, в которой обычно строят новую выборку z_i = x_i - y_i и используют статистические методы анализа одной выборки, а не двух. Проверка однородности для связанных выборок рассматривается ниже.)

При дальнейшем изложении принимаем описанную выше вероятностную модель двух выборок.

Уточнения понятия однородности. Понятие «однородность», т. е. «отсутствие р